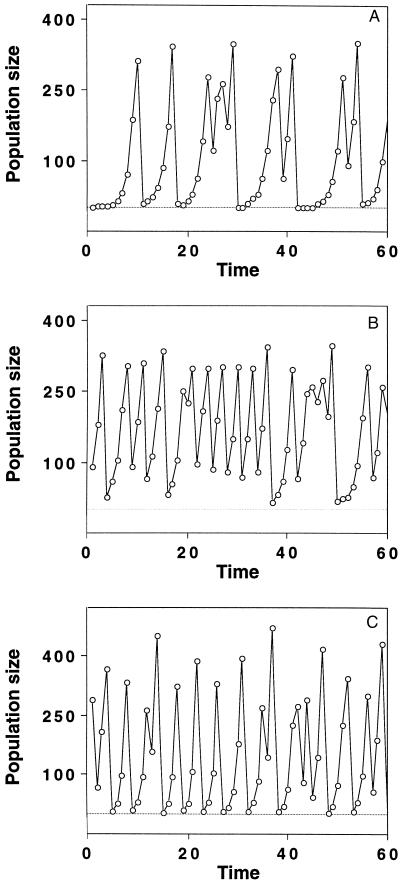
Figure 1.

Three different types of dynamics of Eq. 4. In this model, the dynamic complexity is determined by the intrinsic growth rate λ and by the parameter b, which reflects the type of competition for resources that leads to density dependence. The parameter a scales the carrying capacity of Eq. 4, i.e., the population size at which the per capita fitness F(N), Eq. 5, is equal to 1 (8). For each of the N_t adults at time t, we randomly chose the number of offspring from a Poisson distribution with mean the value of the fitness function, Eq. 5, at the given population size N_t. The offspring add up to give N_t+1. Low values of λ together with high values of b yield crash dynamics with long periods of low population size (A; λ = 2.024, b = 6.8). Decreasing the competition parameter b (B; λ = 2.024, b = 4.5) or increasing λ (C; λ = 3.235, b = 4.8) leads to dynamics in which the long low density periods are absent. Severe crashes still occur with high λ (C). The parameter a was chosen so that the equilibrium density was 250 in all three panels and was set to a = 0.0038 in A, a = 0.0037 in B, and a = 0.0041 C.