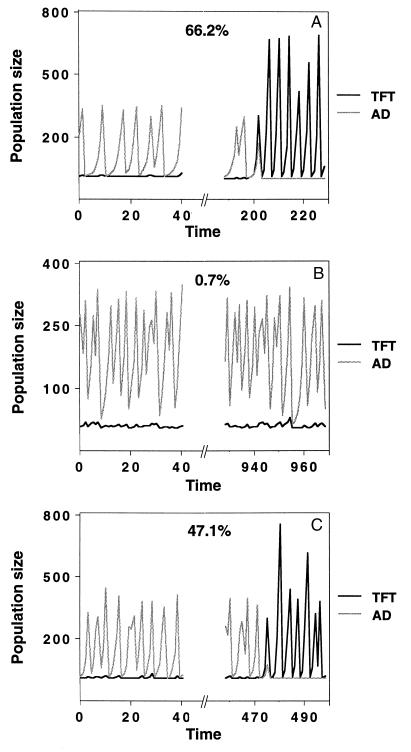
Figure 2.

Invasion scenarios for different types of dynamics of the resident population. Eq. 6 was used with demographic stochasticity. Mutations from AD to TFT occur with a mutation rate that was set to 0.01 per generation. The runs were started with a pure AD population. In A, this resident population exhibited the dynamics shown in Fig. 1A (shaded line). TFT (solid line) typically invades after a short period of time. In B, in which the resident AD population exhibited the dynamics shown in Fig. 1B, the periods of low population size are too short and the crashes not severe enough for TFT to increase above the threshold frequency. In C, the resident AD population exhibited the dynamics from Fig. 1C. With these dynamics, TFT is often able to invade due to stochastic events during population crashes. The percentages shown in the panels indicate the number of times TFT was able to invade the corresponding AD resident in 1,000 simulation runs over 1,000 generations. Due to stochasticity, it is possible that the resident population goes extinct before invasion occurs. In such a case, we initialized the system in the next time step again with a number of resident AD individuals. This number was set to 8 in our simulations and could, for example, be thought of as an influx from neighboring populations in a spatially extended system. The parameters a and b in A–C were the same as the corresponding parameters in Fig. 1 A–C. The parameters for the payoff matrix were w = 0.58, S = 0, P = 0.85, R = 2.1, and T = 3.1 for A and B, and w = 0.66, S = 0, P = 1.1, R = 2.1, and T = 3.1 for C. Thus, the threshold frequency for TFT was p* = 0.539 in all three panels (A–C).