Probabilistic Cross-Species Inference of Orthologous Genomic Regions Created by Whole-Genome Duplication in Yeast

Abstract

Identification of orthologous genes across species becomes challenging in the presence of a whole-genome duplication (WGD). We present a probabilistic method for identifying orthologs that considers all possible orthology/paralogy assignments for a set of genomes with a shared WGD (here five yeast species). This approach allows us to estimate how confident we can be in the orthology assignments in each genomic region. Two inferences produced by this model are indicative of purifying selection acting to prevent duplicate gene loss. First, our model suggests that there are significant differences (up to a factor of seven) in duplicate gene half-life. Second, we observe differences between the genes that the model infers to have been lost soon after WGD and those lost more recently. Gene losses soon after WGD appear uncorrelated with gene expression level and knockout fitness defect. However, later losses are biased toward genes whose paralogs have high expression and large knockout fitness defects, as well as showing biases toward certain functional groups such as ribosomal proteins. We suggest that while duplicate copies of some genes may be lost neutrally after WGD, another set of genes may be initially preserved in duplicate by natural selection for reasons including dosage.

THE discovery of an ancient whole-genome duplication (WGD) in an ancestor of the baker's yeast Saccharomyces cerevisiae (Wolfe and Shields 1997; Dietrich et al. 2004; Kellis et al. 2004) has provided a useful set of duplicate gene pairs, all of equal age, for diverse studies in molecular evolution (e.g., Van Hoof 2005; Conant and Wolfe 2006; Fares et al. 2006; Kim and Yi 2006). In addition, these data provide the opportunity to study the ∼80% of the genes in the S. cerevisiae genome that have returned to single copy since the WGD (Byrne and Wolfe 2005). In particular, because the genomes of several post-WGD yeast species in addition to S. cerevisiae are now available (Cliften et al. 2003; Kellis et al. 2003; Dujon et al. 2004; Scannell et al. 2007), it is possible to study the timing of the various duplicate losses to see if there are any specific differences between the types of duplicate genes lost soon after WGD and those that were retained in duplicate for longer periods.

Data regarding the timing of duplicate gene loss speak to an important theoretical question in molecular evolution, that of understanding how long a newly created duplicate gene pair can be expected to survive the degenerative effects of genetic drift (Nei and Roychoudhury 1973; Li 1980). Analyses of full genomes have shown that duplicate genes are very common in eukaryotes (Lynch and Conery 2000; Rubin et al. 2000), while studies of individual duplicate gene pairs suggest that these pairs can be preserved over long periods (Bisbee et al. 1977; Ferris and Whitt 1977; Hughes and Hughes 1993). These two observations indicate the existence of selective forces that preserve duplicate genes. Among the forces that have been suggested are functional divergence and requirements to maintain high dosages of a gene (Seoighe and Wolfe 1999; Koszul et al. 2004). Generally speaking, functional divergence occurs either through neofunctionalization (the appearance of a novel function in one duplicate; Lynch and Conery 2000; Kondrashov et al. 2002) or through subfunctionalization (the partitioning of ancestral functions between the duplicate pair; Force et al. 1999; Lynch and Force 2000).

Duplicate gene loss itself can drive other evolutionary processes. An analysis of the timings of duplicate gene loss in four post-WGD yeast species (S. cerevisiae, S. bayanus, Candida glabrata, and S. castellii) suggested that a rapid loss of many duplicate pairs contributed to a species radiation after the WGD (Scannell et al. 2006). More recently, we have shown that the yeast Kluyveromyces polysporus split from the lineage leading to S. cerevisiae very soon after the genome duplication. As a result, only 47% of gene duplicates from the WGD in K. polysporus are shared by S. cerevisiae (Scannell et al. 2007).

When comparing such relatively distantly related species that nonetheless share a WGD, duplicate gene loss also complicates inferences regarding molecular evolution. The reason is that the WGD means that a pair of single-copy genes in the two species can share a common ancestor either at the time of their speciation (i.e., they are orthologs) or at the (more ancient) time of WGD (making the two genes paralogs in conventional terminology). Thus, the term paralog can be applied in several distinct ways to genes in genomes where a WGD has occurred. First and most straightforwardly, two genes in a genome surviving in duplicate since the WGD are paralogs of each other. But it is also possible to apply the term to pairs of genes originating from different genomes that share the WGD. In that case, it is helpful to think of two loci (A₁ and A₂) created by WGD from the ancestral single locus A_x. Both loci exist in both species, but each locus (a place on a chromosome) does not necessarily contain a functional gene. Paralogous genes between the genomes are those genes that occupy locus A₁ in species 1 and A₂ in species 2 or vice versa. This distinction is illustrated in Figure 1A, where K. polysporus gene A₁ and S. cerevisiae gene A₂ are paralogs (for illustrative purposes Figure 1A explicitly represents gene losses as pseudogenes, indicated by dashed lines and a “p” prefix). Importantly, in this situation standard methods of identifying orthologs such as reciprocal best BLASTP hits (Altschul et al. 1990, 1997; Tatusov et al. 1997) can spuriously return pairs of paralogs (i.e., K. polysporus gene A₁ and S. cerevisiae gene A₂ in this example). This problem is potentially serious: only 56% of single-copy genes shared by S. cerevisiae and K. polysporus are orthologs according to our previous analysis (Scannell et al. 2007).

Figure 1.—

(A) Illustration of a possible gene phylogeny resulting from WGD. This single genetic locus was first duplicated by WGD (indicated) with the subsequent branchings indicating speciation events. Gene losses also occurred in two instances, shown by dashed lines. For clarity, we label the products of these gene losses as pseudogenes (pA₁ and pA₂), although it is more common for them to be completely deleted. (B) State diagram for the PFS2 and PF2 models. U corresponds to an undifferentiated duplicate state, meaning that either copy may be lost. F indicates that the duplication has been fixed, while S₁ and S₂ are single-copy states. These last three states are “absorbing”: once a locus enters one it remains there permanently. C₁ and C₂ are “partisan” states that can yield convergent gene losses on unrelated branches of the tree. The dashed lines indicate transitions allowed in the PFS2 model (ɛ ≠ 0) but forbidden in the PF2 model (ɛ = 0). The four model states corresponding to the observation of a duplicate pair in the data (D_o) are shaded. (C) Tree inferred from the genomes of five post-WGD species under the PF2 model. Branch lengths are given in terms of αt(2 + 2β + γ). Numbers below each branch are the percentages of genes in states U, F, and C₁ + C₂, respectively. Global parameter estimates are β = 0.120, γ = 0.101, δ = 0.141, and s (probability of a track switching event in Equation 3) = 0.002. The ln likelihood of this tree is −9942.52.

The concept of orthology can be extended to the relationships among chromosome segments or contigs. Our aim then becomes to assign one of each pair of chromosome segments (tracks) in one species as the ortholog of a corresponding segment in a second species. We refer to this problem as “assigning a tracking” and to the resulting segmental orthology assignment as “a tracking.”

By analogy to sequence alignment, the most straightforward approach to assigning orthology between tracks is to maximize the similarity in gene content between the tracks across the species. This approach is taken in the Yeast Genome Order Browser (YGOB) (Byrne and Wolfe 2005). Genomic sections of decreasing length from post-WGD species are placed onto a scaffold derived from non-WGD yeast genomes. Orthology assignments are chosen to avoid the placement of pairs of duplicates descended from WGD (“ohnologs”) onto the same track and to avoid (as much as possible) breaking genomic sections by forcing contiguous genes onto the same track. A second approach, taken by the program ADHoRe, focuses on identifying sections of shared gene content and order, on the basis of thresholds of minimal shared linearity and maximal distance between shared genes (Vandepoele et al. 2002). Because ADHoRe can detect short regions of shared order and allows multiple sections of a genome to show the same shared order, it is especially suited to genomes such as those of plants where multiple WGD events have occurred. In principle, the orthology or paralogy of genomic segments could also be determined using phylogenies inferred from the genes they contain. However, this approach is hampered by several problems, including an inability to incorporate uncertainty in the inferred phylogenies into the analysis, the acceleration in rates of evolution observed after WGD (Fares et al. 2006; Scannell and Wolfe 2008), and the possibility of gene conversion among the loci studied (Pyne et al. 2005; Sugino and Innan 2005). A general overview of the problem of detecting and delimiting genome duplication events is provided by Van De Peer (2004).

The analogy to sequence alignment in the assignment of trackings is meaningful in a second sense as well. If one assumes a particular tracking, then the resulting data can be used to model evolution in a manner similar to that done with aligned sequences. Thus, each ancestral gene (duplicated at WGD) is treated as a “site” that can be observed in one of three states: duplicated, retained only on track 1, or retained only on track 2. A concatenation of these gene-retention states can then be used to infer a phylogenetic tree just as with a set of aligned nucleic acid sites (cf. Scannell et al. 2007).

However, as with sequence alignment and phylogenetic inference, the processes of assigning a tracking and inferring the phylogeny between post-WGD species are not truly independent problems, because the topology inference depends on the correctness of the tracking. Here we introduce a method that probabilistically infers the trackings, the phylogenic topology, and the model parameters simultaneously. Our approach allows us to quantify the confidence with which a pair of genes are assigned as either orthologs or paralogs. By applying this approach to five yeast species we are able to study the question of what forces influence the survival of duplicate genes after WGD.

METHODS

Data sources:

The model described here requires three pieces of input data. First, for each genome analyzed, we need the order of the genes along its chromosomes or contigs; we refer to these as “contig orders.” Second, we need to know whether each gene has any homologs resulting from the WGD. These two pieces of information were extracted from the YGOB (Byrne and Wolfe 2005). The third piece of information is the order of the genes in the ancestral genome just prior to genome duplication, which was estimated by two methods as described in results.

Obtaining the optimal tracking for an ancestral order:

Given an ancestral gene order and the order of the same genes in an extant genome, the question arises how to optimally map the current order onto the ancestral order, given the 2:1 relationship between the two. We define the optimal mapping as the one that imposes the fewest “breaks” on the extant genome. A break is any place in the ordering where two genes that are adjacent to each other in the ancestral order are not adjacent in the extant genome [for example, between K. polysporus genes 380.4 (contig 380) and 1056.15 (contig 1056) in Figure 2].

Figure 2.—

Distribution of the maximal posterior tracking probability across one of the eight inferred ancestral chromosomes. The most probable tracking for two regions is illustrated in detail. The top five tracks and the bottom five tracks are inferred to be two orthologous groups. Lines connect genes that are adjacent on their respective contigs or chromosomes. Along the top are given the posterior probabilities of the tracking depicted (one of a possible 16), calculated from the PF2 model. Between K. polysporus and S. cerevisiae, genes are indicated as single-copy orthologs (green), single-copy paralogs (pink), or where one or both genomes retain the duplication (tan). The red line illustrates how the individual species tracks are constructed, as described in methods. Briefly, we assume that assembly of the tracks is complete to the left and to the right of this line. We then take all possible endpoints to the right of this line (i.e., genes 694.30 and 671.27 in S. castellii) and all possible endpoints to the left (genes 694.29 and 671.28, again in S. castellii) and test whether any joins can be made between the left and right endpoints. In this case two such joins are possible, illustrated with dashed lines in the S. castellii rows.

We obtain the mapping with minimum breaks, using a recursive assembly procedure. First, define t as the smallest integer for which 2^t ≥ x, where x is the number of loci in the current piece of the ancestral order. Starting with the full ordering (x = n, where n is the number of ancestral genes), two subsections of that ordering are produced. The first (a) is of size 2^t−1, and the second (b) is of size x − 2^t−1. If the value of x for section a or section b is >2, a new value of t is determined for that section and the subdivision continues. Once a minimally sized section is reached (x ≤ 2), it is assembled by determining if any of the (up to) four genes in the section are contig neighbors. If they are, they are joined (solid lines in Figure 2). Once these minimal sections have been assembled, the recursion unwinds to sections of size x > 2. At this point, a new joining algorithm is employed. Suppose that we have already completed the recursive assembly of the two sections of Figure 2 separated by the red line (in S. castellii, for instance). We now create a stack consisting of all possible right endpoints of the left section (in this case genes 694.29 and 671.28) and left endpoints of the right section (genes 694.30 and 671.27). We now try every possible combination of left and right endpoints to see if any pair are each other's contig neighbors. In this case, we can join 694.29 to 694.30 and 671.28 to 671.27. We thus add the dashed lines shown in Figure 2. When all requisite joins have been made, the recursion unwinds until the assembly is complete.

The above recursion is not guaranteed to find the minimally breaking mapping if both of a given gene's neighbors appear before, or both after, that gene in the ancestral order. However, this problem can be easily remedied by “breaking” the tracking after every locus, making the above stacks, and checking for improvements.

Modeling gene-content evolution after genome duplication:

We use a modified version of the model of gene loss after genome duplication described in Scannell et al. (2007), a state diagram of which is shown in Figure 1B. Briefly, state U represents undifferentiated duplicated genes that are free to be lost, state F represented duplicate genes being maintained by natural selection, and states S₁ and S₂ are single-copy states. States C₁ and C₂ refer to “partisan” states where the locus remains duplicated but only one copy is available for future loss. Analysis of three post-WGD genomes indicated an excess of parallel losses of the same member of a duplicate pair where the losses could not be attributed to common ancestry (Scannell et al. 2006). To account for this, we allow duplicate pairs to enter a partisan state (states C₁ and C₂ in Figure 1B; Scannell et al. 2007). These states differ from state U in that only copy 2 of a gene may be lost from state C₁ and likewise only copy 1 may be lost from state C₂. We previously required that the rate of loss of duplicate genes from states C₁ and C₂ be equal to rate of loss from state U, but here we apply a more complex parallel losses, fixation, and subfunctionalization with two rates of loss and fixation (PFS2) model shown in Figure 1B. The instantaneous transition rates among the six states are given by

(1)

If δ = 1 and ɛ = γ, this new model degenerates to the model described in Scannell et al. (2007) (PFS1: parallel losses, fixation, and subfunctionalization with a single rate of loss and fixation). The PFS2 model fits our data significantly better than does PFS1 (2Δ ln L = 168.1, P < 0.01). This difference indicates that the value of δ is significantly <1 (see Figure 1C legend); i.e., the rate of gene loss from states C₁ and C₂ is less than that from state U. Interestingly, optimization under the PFS2 model gave ɛ = 0, implying that duplicates never become fixed after they enter states C₁ and C₂ and hence that there is no evidence for duplicate fixation by the route we illustratively referred to previously as “subfunctionalization” (Scannell et al. 2007). This negative finding should not be taken as evidence that subfunctionalization has not happened, but merely that it has not left traces in the patterns of gene loss. This difference between the results with the new data here and the previous data led us to implement a model where we required ɛ = 0 (PF2) that gave the same likelihood as did the PFS2 model and was used for all analyses below. The transition probabilities for the reduced PF2 model are obtained by solving the system of linear differential equations implied in (1) (Lewis 2001) and substituting ɛ = 0:

(2)

Calculating conditional tracking probabilities:

The model above allows us to calculate the probability of the observed gene presence/absence data for any given assignment of orthology between the genes in question. We refer to each orthology assignment as a tracking (Figure 2 illustrates one of the possible trackings for a section of these five genomes). Because there are two possible ways of assigning orthology to a given genome if all other genomes' ortholog assignments are fixed, for n taxa there are 2ⁿ possible trackings. Note that because the definition of “track 1” is arbitrary for the first genome, there only 2ⁿ⁻¹ possibilities that need be considered in subsequent analyses, although we must retain all possible trackings for the calculation itself.

Given the 2ⁿ tracking probabilities at locus i, we can calculate the conditional probabilities of those 2ⁿ possible trackings at locus i + 1 given locus i, using an approach similar to that developed for multilocus genetic linkage analysis by Lander and Green (1987). The vector of these conditional likelihoods at locus i + 1 can be calculated from those at locus i, using

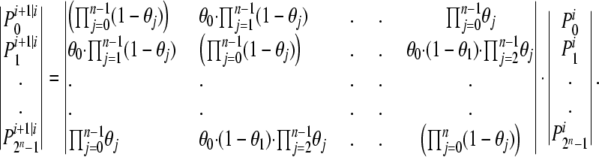(3)

Here, is the likelihood of the jth tracking for the ith locus. Note that 0 ≤ j ≤ 2ⁿ − 1, where n is the number of taxa (indexes run from 0 to 2ⁿ − 1 rather than from 1 to 2ⁿ to allow the use of binary logic operators). θ_j gives the probability of a “track switch” between the two adjacent loci i and i + 1 and can take on one of two values. If no contigs span the gap between loci i and i + 1, then θ_j = 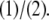This case corresponds to a situation where, for a given species, no line joins i to i + 1 for either track (for instance, between K. polysporus genes 380.4 and 1056.15 in the bottom right of Figure 2). Otherwise, θ_j is given by a global constant s that is estimated from the data by maximum likelihood. The value of s can be thought of as an error term that allows for inconsistencies in the ancestral ordering, errors in the identification of WGD loci, and genuine historical signals of recombination in the genomes. In general s is small for our analyses (≈ 0.002). To calculate the likelihood of the entire data set, we iteratively apply Equation 3 starting at the first locus in the genomes, yielding at locus i a vector 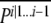(likelihood of each tracking at locus i given loci 1 … i − 1). For the final locus, the sum of the elements in this vector is the likelihood of the data set. Maximum-likelihood values of the model parameters are estimated using purpose-written software and standard numerical optimization (Press et al. 1992).

Modeling genome duplication:

When using gene order data it is important to account for potentially missing sequence data. For instance, in Figure 2, no contig spans the top track for S. castellii following gene 694.32. There are two potential reasons for this absence. Said genes may have been “truly” lost from their positions on one of the contigs on either side of the gap. However, it is also possible that a gene exists in the genome for that position but was missed by the genome sequencing effort (e.g., the S. castellii genome sequence is an incomplete draft; Cliften et al. 2003, 2006). To overcome this problem, we have treated such sites as missing data, probabilistically allowing for the possibility of missing duplicates. Model parameter estimates do not differ greatly if all such positions are treated strictly as gene losses (data not shown).

Hypothesis testing using the model:

To test for evidence of a significant shared branch between K. polysporus and S. cerevisiae, we first simulated genomes under the assumption that this branch was of zero length. To recreate genomes with features similar to the real ones studied, we produced pseudogenomes with the same contigs and order seen in the real data. We then created the genome duplication by replacing all single-copy genes with duplicates that appear in their appropriate syntenic context. In cases where doing so requires creating genes in gaps between two contigs (such as the example opposite S. castellii gene 694.32 in Figure 2), the next contig was arbitrarily extended to include the new genes. Losses were then simulated using the model parameters inferred from the real data under the assumption of a zero-length branch at the root. These simulated data sets were then analyzed under that model and also under a model where the root branch length was unconstrained and the difference in likelihood between the two models calculated. The resulting distribution of Δ ln L (difference in log-likelihood) was then compared to the difference seen in the real data. An identical approach was taken for testing the hypotheses that model parameters β and γ were nonzero (see results).

Factors influencing timing of gene losses:

For all analyses of the effect of genomic factors on gene loss timings, we removed from our data set those orthologs with a posterior probability of ≥0.1 of having been lost after passing through states C₁ or C₂ (see results). Since these losses result in retention of orthologs but may have happened well after the speciation in question, they may be more similar to paralogs in terms of the types of selection acting on the genes in question. Keeping these orthologs in our data set alters our conclusions for only a single comparison, with the mRNA levels showing a marginally significant difference between the paralogs and the orthologs in the S. cerevisiae to K. polysporus comparison (P = 0.038). Calculation of the inherent rate of evolution of a gene is complicated by WGD as the period following duplication may have been characterized by altered selective constraints (Nembaware et al. 2002; Scannell and Wolfe 2008). To avoid this problem, we followed our previous approach of calculating the rate of sequence evolution for a locus, using the two non-WGD species K. lactis and Eremothecium gossypii (Scannell et al. 2007).

Data from Lee et al. (2002) on transcription factor binding were filtered to exclude bindings with false-positive probabilities >0.001. Data on the fitness effects of gene knockouts were taken from Steinmetz et al. (2002). We averaged the knockout fitness on YPD media for the two time courses and omitted genes where these values differed by >0.05. Following Gu et al. (2003), we then normalized these measurements by the average value across all genes. Any gene annotated as essential by MIPS (Mewes et al. 1999) was assigned a fitness value of zero.

RESULTS

Modeling gene loss after genome duplication:

In previous work (Scannell et al. 2007) we introduced a maximum-likelihood approach to modeling gene loss after genome duplication (Felsenstein 1981; Lewis 2001). Because this model is based on data regarding the presence or absence of particular genes in a genome, it will not be able to answer all biologically interesting questions about the loss or preservation of a pair of duplicate genes produced by WGD. In particular, the model allows for the fixation of a duplicate gene pair created by WGD but does not distinguish between preservation by neofunctionalization and preservation by subfunctionalization.

The data consist of loci duplicated at WGD that can be observed in one of three states: S₁ (a single copy of the gene is present at locus A₁), S₂ (a single copy is present at A₂), and D_o (duplicate copies of the gene are present). To more completely model the process of duplicate loss, the observed D_o state is partitioned among four nonobservable states (shaded in Figure 1B). State U consists of duplicate gene pairs that are redundant, meaning that either copy can be lost through genetic drift. Immediately after the WGD all loci are assumed to be in this state. State F represents fixed duplications that are preserved indefinitely. We do not discount the possibility that future changes in ecological niche or competitors could allow the loss of a “fixed” duplicate, but we do not incorporate this possibility into our model. States C₁ and C₂ are states used to model convergent losses of genes in independent lineages (see methods).

Probabilistic track assignment:

Our original analysis assumed that every single-copy gene in a post-WGD genome could be unambiguously assigned as either a paralog or an ortholog of the corresponding genes in the other species (the “alignment” problem described in the Introduction; Scannell et al. 2007). However, to ensure that such assignments were correct, it was necessary to exclude many regions of the genomes, and we developed a heuristic concept of the “robustness” of tracking (Byrne and Wolfe 2005). Because the genome of K. polysporus is rather distantly related to the other genomes studied and because its genome assembly contains a number of short contigs, orthology assignment is difficult for this species: in the previous analysis, only 2299 loci from the WGD could be analyzed (Scannell et al. 2007). Here we are able to increase this number to 4107 loci.

We probabilistically assign orthology to each locus on the basis of the status of the neighboring loci and the model of gene loss as described above. In the special case where all species have retained duplicate genes at a locus, all 2ⁿ possible trackings are equally probable. In other cases, the probability of each tracking will depend on the branch lengths of the phylogenetic tree of the species and the values of the parameters β, γ, and δ. In supplemental Tables 1 and 2, we provide the probabilities of all 16 possible trackings for each ancestral locus considered as well as a listing of the most likely tracking and its associated probability.

Effect of assumed ancestral order on inferences:

To calculate the above likelihoods, we need to consider all the loci in the genomes in a uniform order across all genomes (i.e., we need to know that locus i + 1 appears after locus i in Equation 3). Although one could use the extant order in any one genome and impose breaks on the other genomes where they differed, a more appropriate method is to attempt to infer the gene order that existed in the ancestral genome just prior to WGD. Here, we compared the results obtained using two possible gene orderings. Our first approach simply assumes that the extant gene order in the non-WGD species K. lactis represents the gene order immediately prior to WGD. The second approach uses a candidate “ancestral” gene order that was inferred using a parsimony analysis applied to the complete set of available non-WGD and post-WGD species (J. L. Gordon and K. H. Wolfe, unpublished data; this order is visible on the YGOB website). In Figure 3, we compare the posterior tracking probabilities for these two possible orderings. There are a fairly large number of disagreements between the two orders (2628 agreements vs. 1411 disagreements; solid vs. shaded points in Figure 3). Note, however, that most of these disagreements are cases where one or both orderings give low posterior probability: of the 1481 loci where the most probable tracking accounts for ≥75% of the total probability, 1332 (90%) agree between the two orderings. It is also clear that the presumed ancestral ordering in general gives higher posterior tracking probabilities than does the current K. lactis ordering. For this reason, we used the ancestral ordering for our subsequent analyses.

Figure 3.—

Comparison of maximal posterior tracking probabilities for two possible orderings of the ancestral genome. In the center is a scatter plot for each of 4039 loci in both orderings. For each locus the y-axis gives the posterior probability when the modern K. lactis genome is used to define the ancestral ordering, and the x-axis gives this same probability when an ancestral order inferred from all genomes in YGOB is used. Solid points are those where the two orderings agree on the most probable tracking, and shaded points are cases of disagreement. Histograms of the distribution of posterior probabilities are shown for the ancestral ordering (bottom graph) and the K. lactis ordering (right-hand graph).

Confirmation of previous phylogeny and model effects:

It is still debatable whether S. castellii or C. glabrata is more closely related to S. cerevisiae (Kurtzman and Robnett 2003; Hedtke et al. 2006; Scannell et al. 2006). Thus, we inferred the phylogeny in Figure 1C by optimizing the likelihoods of all 105 possible trees and retaining the maximum-likelihood topology (this was also the topology found in the previous analysis; Scannell et al. 2007). We also used simulation to determine whether there was evidence that γ ≠ 0 and β ≠ 0, finding that both these parameters were significantly nonzero (2Δ ln L = 14.6, P < 0.01 and 2Δ ln L = 213.8, P < 0.01, respectively).

Confirmation of a single, shared genome duplication:

Because our previous conclusion of a single shared genome duplication between S. cerevisiae and K. polysporus (Scannell et al. 2007) rested on a track-assignment approach that essentially maximized the degree of shared gene loss between the species (Byrne and Wolfe 2005), it is in principle possible that the shared ancestry seen was spurious. To test for this possibility, we reanalyzed these genomes with the above track-inference approach that makes no assumptions as to shared ancestry. We find evidence for a significantly nonzero shared branch (shared genome duplication) predating the split between K. polysporus and S. cerevisiae (2Δ ln L = 316.1, P < 0.01; see methods). In fact, the percentage of genes converted to single copy along the shared branch is inferred to be slightly greater than was previously found (19.6 vs. 17.5%). We also estimate that ∼1% of all loci duplicated by WGD were fixed in duplicate by the time of the split between these two species.

Identifying high-confidence orthologs and paralogs:

Given the estimated model parameters (including the tree topology and branch lengths), we can, for every locus in our ancestral genome order, determine the posterior probability of each of the 2ⁿ⁻¹ unique trackings. In Figure 2, we show how the probability of the most likely tracking varies across an ancestral chromosome. We also illustrate two reference sections of that chromosome, with the probability of the mostly likely tracking (the one shown) indicated at the top of each column.

For any two post-WGD species, a pair of single-copy genes can be either paralogs or orthologs. The model used here assigns probabilities to these two possibilities. In Figure 4, we show how the proportion of orthologs between S. cerevisiae and K. polysporus varies across loci according to the confidence in the most probable tracking. Not surprisingly, regions with relatively more orthologs have higher maximal tracking probabilities, because our model assigns a higher probability to a shared loss event leading to a pair of orthologs than to independent loss events leading to two paralogous genes.

Figure 4.—

The proportion of orthologs in a region of the genome decreases as the level of uncertainty in the tracking increases (i.e., the maximal tracking probability decreases). We plot the cumulative proportion of orthologs between S. cerevisiae and K. polysporus in all loci whose maximal posterior tracking probability is ≥x.

For the species pairs S. cerevisiae/K. polysporus, S. cerevisiae/S. castellii, and S. cerevisiae/C. glabrata, we constructed data sets of high-confidence single-copy orthologs and of high-confidence single-copy paralogs (Table 1). For each pair, we did so by summing the posterior probabilities of all possible trackings in the remaining three species to give P_o or P_p: the probability that a given locus is an ortholog or a paralog, respectively. We required P_o, P_p ≥ 0.9. Because paralogous pairs must have been lost independently after speciation, on average they represent more recent gene losses than do the orthologs. We then examined the properties of these gene sets, as described below.

TABLE 1.

Number of high-confidence (>0.9) orthologs and paralogs for three species-pair comparisons

Species pair	No. orthologs	No. paralogs
S. cerevisiae/K. polysporus	873 (848)a	463 (444)
S. cerevisiae/S. castellii	3066 (3010)	314 (296)
S. cerevisiae/C. glabrata	3335 (3239)	143 (131)

^aThe number in parentheses is the number of genes in each category where for each gene the probability of having passed through either of the convergent states C₁ or C₂ is <0.1 (see methods).

Genomic factors affecting timing of duplicate loss:

We found a general tendency for paralogous genes in more recently diverged genomes to have higher protein abundance (measured in S. cerevisiae; Ghaemmaghami et al. 2003) than orthologs (t-test, P < 10⁻⁸ and P < 10⁻⁴, for the comparisons of S. cerevisiae to S. castellii and of S. cerevisiae to C. glabrata, respectively; see supplemental Figure 1), but no such tendency for the comparison of S. cerevisiae to K. polysporus (P = 0.99, supplemental Figure 1). These observations suggest that genes with high abundance in the cell tended to survive in duplicate for longer periods after WGD than did other genes. This effect extends to the surviving duplicates in S. cerevisiae: compared to the S. cerevisiae/K. polysporus orthologs (many of which were lost soon after WGD), individual duplicate genes tend to be present in greater abundance (P = 0.003, supplemental Figure 1).

These results echo our previous observation that genes retained in duplicate for longer time periods tend to be more slowly evolving (Scannell et al. 2007), as protein abundance is inversely correlated with the rate of sequence evolution (Drummond et al. 2006). We thus tested seven genetic factors for association with the timing of gene loss. We examined three factors related to gene expression: the codon adaptation index (CAI) (a measure of codon usage bias and hence of expression; Sharp and Li 1987), the number of protein molecules per cell (protein abundance; Ghaemmaghami et al. 2003), and the number of mRNA molecules per cell (Holstege et al. 1998). Two properties of cellular networks were considered: the number of transcription factors binding upstream of the gene (data from Lee et al. 2002) and the number of protein interactions that the gene's product is involved in (the Database of Interacting Proteins core data set; Xenarios et al. 2000; Salwinski et al. 2004). Finally, more generalized measures of protein evolutionary “dispensability” were considered (see methods): the inherent rate of sequence evolution (Scannell et al. 2007) and the fitness defect of the gene knockout (Mewes et al. 1999; Steinmetz et al. 2002). Using data sets of high-confidence orthologs and paralogs (Table 1), we tested the association between each variable and whether a particular gene was a paralog, using logistic regression (Sokal and Rohlf 1995). We find that for paralogs produced after the S. cerevisiae/S. castellii split and after the S. cerevisiae/C. glabrata split, all seven variables are significantly different than for the corresponding orthologs (Table 2), with the sole exception of the number of transcription factor binding sites in the S. cerevisiae/S. castellii comparison. No factors show a significant association with paralogy for the S. cerevisiae/K. polysporus comparison (Table 2).

TABLE 2.

Association between various genetic factors and the probability of a pair of single-copy loci in S. cerevisiae and an outgroup being paralogs

Variable	Outgroup species	Prediction slope (m)a	Prediction intercept (b)	P(m = 0)b
No. of transcription factors bound	K. polysporus	−0.031	−0.630	0.56
	S. castellii	0.047	−2.35	0.37
	C. glabrata	0.176	−3.33	0.004
No. of protein–protein interactions	K. polysporus	−0.006	−0.632	0.59
	S. castellii	0.030	−2.42	0.001
	C. glabrata	0.027	−3.30	0.034
Codon adaptation index (CAI)	K. polysporus	0.375	−0.709	0.58
	S. castellii	3.02	−2.85	<10−8
	C. glabrata	4.40	−4.05	<10−12
Rate of evolution	K. polysporus	0.226	−0.748	0.60
	S. castellii	−3.04	−1.27	<10−10
	C. glabrata	−4.58	−1.66	<10−11
Log10(protein abundance)	K. polysporus	−0.0001	−0.648	0.98
	S. castellii	0.691	−4.77	<10−8
	C. glabrata	0.801	−6.02	<10−6
Log10(mRNA abundance)	K. polysporus	0.219	−0.635	0.086
	S. castellii	0.951	−2.39	<10−12
	C. glabrata	1.52	−3.41	<10−17
Fitness after knockout	K. polysporus	0.135	−0.667	0.33
	S. castellii	−0.991	−1.68	<10−12
	C. glabrata	−1.19	−2.47	<10−9

^aData were fit to the logistic regression model , where x is the predictor of interest. Parameter b gives the natural log of the odds of a gene being a paralog when the predictor x = 0.

^bProbability of m = 0 under a likelihood-ratio test. Underlined values are significant at P ≤ 0.05.

Many of the factors in Table 2 are intercorrelated (see Drummond et al. 2006), so it is reasonable to ask which of them are independent predictors. To address this issue, we fit a model containing all seven predictors to the high-confidence orthologs and paralogs inferred by comparing S. cerevisiae and C. glabrata. We then sequentially removed the weakest nonsignificant predictor until all remaining predictors were significant. Doing so produces the surface shown in Figure 5, with mRNA abundance and knockout fitness being the two remaining significant predictors. Note that these two effects have independent predictive power—removing either one significantly reduces the quality of fit (P < 10⁻⁴, likelihood-ratio test) and the magnitude of each predictor's effect on the probability of a gene being a paralog decreases only slightly (<25%) when the other predictor is included compared to when the original predictor is used alone. The two predictors are also only weakly correlated with each other (Pearson's r = −0.14), again suggesting the independence of their effects.

Figure 5.—

Predicted effect of two genetic factors on the probability of a pair of single-copy homologs from S. cerevisiae and C. glabrata being paralogs. The surface shows the predicted probability of being a paralog under a logistic regression model as a function of that locus's mRNA abundance and knockout fitness in S. cerevisiae. This surface is described by the equation , where x is the log₁₀ mRNA abundance and y is the knockout fitness. The line drawn on the surface shows where the horizontal plane describing the overall probability of being a paralog (P_paralog = 0.041) intersects this prediction surface.

Functional differences between early and late losses:

We also compared the annotations of the high-confidence single-copy orthologs inferred for the species pair S. cerevisiae/C. glabrata to those of the corresponding single-copy paralogs, using the yeast GO-Slim process classification (Cherry et al. 1998; Gene Ontology Consortium 2000). By far the most overrepresented term among the paralogs was “ribosome biogenesis and assembly” (P < 10⁻⁶ by a chi-square test with a Bonferroni correction for 33 hypothesis tests). It is intriguing that there is also a strong overrepresentation of ribosomal proteins among the surviving WGD duplicates in S. cerevisiae (Seoighe and Wolfe 1999) and that at least one ribosomal protein pair duplicated at WGD confers a dosage-dependant selective advantage (Koszul et al. 2004). We suggest that dosage selection preserves some duplicate genes after WGD with the occasional release of dosage constraints allowing duplicate loss, yielding an overall slow rate of duplicate loss among these genes. Further supporting the plausibility of dosage selection is the observation that one ribosomal protein gene (RPL25), which exists as a single-copy paralog between S. cerevisiae and C. glabrata, survives in duplicate in S. castellii, where the two duplicate copies show >97% sequence identity at the amino acid level, suggesting minimal functional divergence between the two copies.

DISCUSSION

We developed a model of genome evolution following WGD that addresses several questions surrounding this event. A number of our previous observations (Scannell et al. 2007), including the phylogeny of the five species in question and the importance of duplicate fixation and partisan loss, were confirmed. We have also verified that the WGD is shared by S. cerevisiae and K. polysporus despite their limited number of shared duplicate genes and gene loss events. Interestingly, we found evidence for a category of slowly resolving duplicate loci (states C₁ and C₂), where the rate of duplicate loss is more than seven times slower than that of duplicates in state U (δ = 0.141 for Figure 1C). We also found that other loci can become fixed in duplicate (transitions from states U to F), but there is no evidence for transitions to state F from states C₁ or C₂. These two features (partisan loss and fixation) both significantly improve the fit of the model and argue for the action of natural selection on how duplicates are lost. We hypothesize that this action is in the form of purifying selection, whereby some duplicate loci cannot be lost (state F), while others can undergo gene loss only after the release of some selective constraint (states C₁ and C₂). For example, a gene with high dosage requirements may be maintained in duplicate until a mutation raises the expression of one copy sufficiently to allow the loss of the other copy, as has been previously argued by Scannell and Wolfe (2008). Such dosage constraints have been treated theoretically in the quantitative subfunctionalization model of Force et al. (1999). This hypothesis is supported by our observation of an excess of ribosome biogenesis genes among genes with recently lost duplicates, since ribosomal proteins can be maintained in duplicate by dosage selection. We also note that surviving WGD-produced duplicate genes tend to be highly expressed in both yeast and Paramecium tetraurelia (Seoighe and Wolfe 1999; Drummond et al. 2005; Aury et al. 2006).

Natural selection is also indicated in our analysis of the influence of genomic factors on the timing of gene loss. Gene expression levels are generally higher for genes whose duplicate partner was lost after the split of C. glabrata and S. cerevisiae compared to those whose partner was lost earlier. It also appears that less dispensable genes are more likely to have survived in duplicate until this point. While it is intuitively straightforward to imagine a dosage constraint on the loss of a duplicate gene, it is less clear how loss rates are associated with the knockout fitness defect of the surviving gene copy. We find that a single-copy gene in S. cerevisiae is more likely to have a single-copy paralog in C. glabrata if it is essential than if it is dispensable (Figure 5). One possible explanation for this observation is that duplicate pairs are retained to buffer against deleterious mutations (Gu et al. 2003), although this would require selection for mutational robustness, which is theoretically problematic (Cooke et al. 1997; Nowak et al. 1997). One could also argue that if WGD creates functionally divergent paralogous networks (Conant and Wolfe 2006), where most members are duplicates derived from WGD, those network members that revert to single copy might consequently show strong essentiality due to their dual roles.

We suggest that our results support Ohno's original contention that WGD is an important route to functional innovation because it is able to overcome constraints on gene dosage (Ohno 1970), an insight supported by a recent analysis of 17 fungal genomes (Wapinski et al. 2007). Yeast exhibits constraints of this nature (Papp et al. 2003), suggesting that not just the absolute expression level (Figure 5) but also the relative expression levels between gene copies may be of importance in determining when a duplicate gene may be lost. In this vein, we note that in Arabidopsis thaliana functional categories of gene duplicates that survive from WGD tend not to have duplicates survive from other duplications (Maere et al. 2005), just as would be expected if the duplicates preserved from WGD were constrained in relative dosage and hence could not be duplicated independently.

Whatever the role of natural selection late in the resolution of the WGD, it appears that the early gene losses (those occurring around the time of the split of K. polysporus from the remaining species) resulted primarily from genetic drift. This is an interesting conclusion, suggesting as it does that there are both dosage-sensitive and dosage-insensitive loci in the yeast genome that respond differently to WGD. Such a distinction has previously been suggested by the fact that functional categories of genes seem to have had similar responses to WGD in several independent genome duplications (Paterson et al. 2006).

Our approach to modeling genome evolution after WGD is general enough to be applied to other species complexes that share a WGD when such genomic sequences become available. The method has several useful features, including the ability to quantify our confidence in the assignment of orthology to each region of the genome. It also provides a framework for hypothesis testing (for instance, regarding the phylogeny of the species involved) and could allow the comparison of patterns of evolution after WGD among different taxonomic groups.