Permeation and Gating in Ca_V3.1 (α1G) T-type Calcium Channels Effects of Ca²⁺, Ba²⁺, Mg²⁺, and Na⁺

Abstract

We examined the concentration dependence of currents through Ca_V3.1 T-type calcium channels, varying Ca²⁺ and Ba²⁺ over a wide concentration range (100 nM to 110 mM) while recording whole-cell currents over a wide voltage range from channels stably expressed in HEK 293 cells. To isolate effects on permeation, instantaneous current–voltage relationships (IIV) were obtained following strong, brief depolarizations to activate channels with minimal inactivation. Reversal potentials were described by P_Ca/P_Na = 87 and P_Ca/P_Ba = 2, based on Goldman-Hodgkin-Katz theory. However, analysis of chord conductances found that apparent K_d values were similar for Ca²⁺ and Ba²⁺, both for block of currents carried by Na⁺ (3 μM for Ca²⁺ vs. 4 μM for Ba²⁺, at −30 mV; weaker at more positive or negative voltages) and for permeation (3.3 mM for Ca²⁺ vs. 2.5 mM for Ba²⁺; nearly voltage independent). Block by 3–10 μM Ca²⁺ was time dependent, described by bimolecular kinetics with binding at ∼3 × 10⁸ M⁻¹s⁻¹ and voltage-dependent exit. Ca²⁺_o, Ba²⁺_o, and Mg²⁺_o also affected channel gating, primarily by shifting channel activation, consistent with screening a surface charge of 1 e⁻ per 98 Ų from Gouy-Chapman theory. Additionally, inward currents inactivated ∼35% faster in Ba²⁺_o (vs. Ca²⁺_o or Na⁺_o). The accelerated inactivation in Ba²⁺_o correlated with the transition from Na⁺ to Ba²⁺ permeation, suggesting that Ba²⁺_o speeds inactivation by occupying the pore. We conclude that the selectivity of the “surface charge” among divalent cations differs between calcium channel families, implying that the surface charge is channel specific. Voltage strongly affects the concentration dependence of block, but not of permeation, for Ca²⁺ or Ba²⁺.

INTRODUCTION

It seems like a simple experiment: determine the concentration dependence of current through a voltage-dependent Ca²⁺ channel by varying the concentration of Ca²⁺. But it has long been recognized that interpretation of such results is complicated. In particular, the whole-cell current is affected by gating as well as permeation. Ions can modify gating by a variety of mechanisms, including screening of surface charge (Frankenhaeuser and Hodgkin, 1957), effects of pore occupancy on gating (Swenson and Armstrong, 1981), and binding to sites outside the pore (Gilly and Armstrong, 1982).

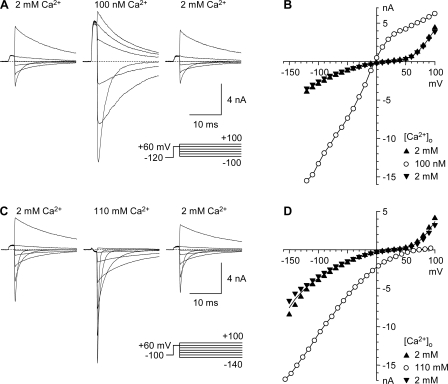
The classical method for separating gating from permeation is the instantaneous current–voltage relationship (IIV) (Hodgkin and Huxley, 1952). Channels are first activated by a fixed depolarizing pulse, followed by repolarization to a wide range of voltages. The current measured “instantaneously” at each new voltage reflects the current through the population of channels opened by the prior depolarizing pulse (Fig. 1). Thus, the number of channels open is constant, so any variation in current must reflect the effect of voltage on permeation through those open channels. The IIV method makes several assumptions, most critically that currents can be accurately measured before gating processes affect the number of channels open (see Materials and methods).

Figure 1.

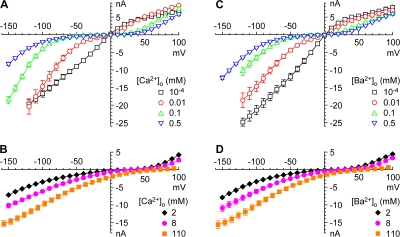
The instantaneous current–voltage protocol (IIV) used to examine permeation and block. (A and C) Currents recorded in 2 mM Ca²⁺_o, a test solution (100 nM Ca²⁺_o in A, 110 mM Ca²⁺_o in C), and following return to 2 mM Ca²⁺_o (shown from left to right, in 40-mV increments). For this and all figures illustrating current records, dashed lines indicate zero current following leak subtraction. 3 kHz digital Gaussian filter. (B and D) IIV relations measured from the initial amplitude of single-exponential fits (see Materials and methods), following a brief strong depolarization (2 ms to +60 mV) to produce maximal activation with minimal inactivation. Values in 2 mM Ca²⁺_o recorded before and after application of the test solution are shown as upward and downward triangles (respectively), with a line drawn through the average. Voltages in 110 mM Ca²⁺_o (D) are corrected for a junction potential (see Materials and methods).

Gating of Ca_V3.1 is sufficiently slow for the IIV to be measured over a wide voltage range (Serrano et al., 1999, 2000). In this study, we examine the concentration dependence of current from 100 nM to 110 mM Ca²⁺ (or Ba²⁺), from +100 to −150 mV. This dataset provides a detailed yet large-scale view of how voltage and ion concentration affect permeation. One major goal was to examine the basis of selectivity between Ca²⁺ and Ba²⁺, for a channel that exhibits similar ionic currents with the two ions, but is selective for Ca²⁺ by other criteria (Serrano et al., 2000).

We also found that divalent cations modify gating, by two distinct mechanisms. First, Ca²⁺, Ba²⁺, and Mg²⁺ shift channel activation, in a manner largely consistent with screening of surface charge. This contrasts with high voltage–activated (HVA) Ca²⁺ channels (Byerly et al., 1985) and Na⁺ channels (Hille et al., 1975), where Ca²⁺ has larger effects than Ba²⁺ or Mg²⁺, suggesting that Ca²⁺ can both bind to and screen surface charges. This implies that some or all of the “surface charge” is specific to a particular ion channel. Second, Ba²⁺ speeds inactivation of inward currents (compared with Ca²⁺ or Na⁺), and the effect correlates with pore occupancy.

MATERIALS AND METHODS

Whole-Cell Recording

Whole-cell recordings were performed from HEK293 cells stably transfected with rat Ca_V3.1 (Lee et al., 1999) as previously described (Serrano et al., 1999). Data were recorded at room temperature using an Axopatch 200 amplifier driven by pClamp software (pClamp 8.2, Axon Instruments). Electrode resistances were 1.5–2 MΩ, giving series resistances in the whole-cell configuration of 3.8 ± 1.2 MΩ (mean ± SD, 57 cells) before compensation, usually with “correction” at 80–90% and “prediction” at 40–60%. Data were sampled at 50 kHz following 10 kHz analogue filtering using the amplifier. Both “raw” and leak-subtracted currents were recorded, and all current records and analyses shown are from leak-subtracted data. The holding potential was −100 mV, except −120 mV in 0.1 or 10 μM Ca²⁺_o or Ba²⁺_o (to avoid possible resting inactivation).

Recording Solutions

The standard intracellular solution contained (mM) 120 NaCl, 11 EGTA, 2 CaCl₂, 1 MgCl₂, 4 MgATP, 10 HEPES, pH 7.2, with 2 M NaOH. Ca²⁺_i = 40 nM, Mg²⁺_i = 1.0 mM, and total Na⁺_i,o = 145 mM including NaOH used for titration. Experiments with low Mg²⁺_i (Fig. S15) used either a nominally 0 Mg²⁺-0 ATP intracellular solution (120 NaCl, 2 CaCl₂, 8 glucose, 11 EGTA, 10 HEPES, pH 7.2), or an intracellular solution calculated to have 0.2 mM free Mg²⁺ (120 NaCl, 2 CaCl₂, 2.91 MgCl₂, 4 Na₂ATP, 11 EGTA, 10 HEPES, pH 7.2), as specified in the figure legend. Calculated free Ca²⁺ and free Mg²⁺ in buffered intracellular and extracellular solutions are from MaxChelator v. 2.5 (Patton et al., 2004) at the URL address http://www.stanford.edu/∼cpatton/maxc.html. Comparable values were obtained using the program CHELATOR (Schoenmakers et al., 1992).

The standard extracellular solution contained (in mM) 140 NaCl, 2 CaCl₂ or BaCl₂, 10 HEPES, 10 glucose, pH 7.2 with 2 M NaOH. In experiments where Ca²⁺_o or Ba²⁺_o concentrations were changed, NaCl_o was maintained constant at 140 mM, except in isotonic 110 mM solutions where no NaCl_o was included and the pH was adjusted using NMDG base. When Mg²⁺_o was added, the extracellular NaCl concentration was maintained constant at 140 mM, except NaCl was reduced to 119 mM in 30 mM Mg²⁺. Where noted (Fig. S20), NaCl_o was fully or partially replaced by equimolar NMDG·Cl_o (prepared by titration of NMDG base with HCl).

Low Ca²⁺_o concentrations were achieved with 1 mM EGTA (0.1 μM free Ca²⁺_o, with 0.379 mM total Ca²⁺_o) or 1 mM HEDTA (3 or 10 μM free Ca²⁺_o, with 0.334 mM or 0.633 mM total Ca²⁺_o respectively). However, we found that block of inward currents carried by Na⁺ was significantly faster and more potent when 10 μM Ca²⁺ was added directly to a nominally Ca²⁺-free extracellular solution than with our HEDTA-buffered 10 μM Ca²⁺ solution, as if the actual free Ca²⁺_o was ∼1.6× higher in the unbuffered solution (see Fig. S1, available at http://www.jgp.org/cgi/content/full/jgp.200809986/DC1). Extracellular solutions with nominally zero Ca²⁺ had <3 μM total Ca²⁺, as measured by atomic absorption flame spectroscopy (Perkin Elmer Atomic Absorption Spectrometer 3100), consistent with the block of current carried by Na⁺ by nominally Ca²⁺-free extracellular solution with no added calcium buffer (Fig. S1 B). We attempted to calibrate the Ca²⁺-HEDTA system, using arsenazo III or Fura 6F as calcium indicators, but we have not obtained results with sufficient reproducibility and precision to measure the K_d for HEDTA (not depicted). Since EGTA-like buffers may bind contaminating cations possibly contained in unbuffered solutions, the data we present here with 3 or 10 μM Ca²⁺ are with HEDTA-buffered solutions.

Junction Potentials and Activities

For most experiments, extracellular solutions were exchanged using a multibarrel perfusion system, with flow driven by gravity, and an Ag/AgCl ground electrode in the bath. This configuration results in a liquid junction potential between the perfusing solution and the bath. The effect of the junction potential in the measurement of the membrane potential (V_M) was calculated (Neher, 1992):

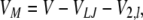(1)

where V is the command potential, V_LJ is the liquid junction potential between the 2 mM Ca²⁺ sealing (also control) solution and the intracellular solution, and V_2,1 is the liquid junction potential established between the 2 mM Ca²⁺ control solution and the test solution. Liquid junction potentials were calculated using a generalized Henderson equation implemented in the JPCalc software (Barry, 1994) that is incorporated into Clampex (Axon Instruments). V_LJ in our experimental conditions is 0 mV, but V_2,1 ranged from −0.3 in low Ca²⁺ concentrations to 6.9 mV in isotonic CaCl₂ solutions. Junction potentials in isotonic CaCl₂ solutions were confirmed experimentally using a 100-μl perfusion chamber grounded with a 3 M KCl 3% agar bridge, in the current clamp configuration of the Axopatch 200 amplifier. Measurements were corrected only for junction potentials calculated to be >1 mV. For analyses where values had to be compared directly at each voltage, values with significant junction potentials were linearly interpolated to the desired voltage (Fig. 5, Fig. S12, E and F, and Fig. S20 E). Original current records in Fig. 1 C, Fig. S5 C, Fig. S11, and Fig. S20 A are not corrected for junction potentials.

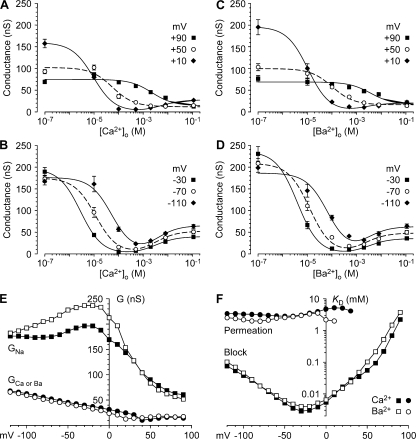
Figure 5.

Analysis of chord conductances. (A–D) Dependence of chord conductance on Ca²⁺_o or Ba²⁺_o, shown for voltages in 40-mV increments. Positive voltages (A and C) and negative voltages (B and D) are shown for Ca²⁺_o (A and B) and Ba²⁺_o (C and D). Smooth curves are described in Materials and methods. (E and F) Analysis of chord conductances as the sum of Na⁺ and Ca²⁺/Ba²⁺ conductances. (E) Maximal conductances; (F) apparent K_d values for permeation (activation of G_{Ca or Ba}) and block (inhibition of G_Na).

For the experiments in Fig. S20, B and F–H, solutions were changed by bath superfusion (including exposure of the 3 M KCl 3% agar bridge ground electrode to the test solution). This procedure does not result in a change in junction potential for the whole-cell recording configuration, so no correction was necessary.

Where noted, thermodynamic activities were calculated for Na⁺, Ca²⁺, and Mg²⁺ in mixed solutions where Cl⁻ was the major anion, multiplying each ion concentration by the activity coefficient calculated using Pitzer's formalism (Pitzer and Mayorga, 1973; Harvie and Weare, 1980; Anderson and Crerar, 1993).

Whole-Cell Protocols and Analysis of Permeation

In each ionic condition, currents were recorded with two protocols, which we call the IIV protocol (Fig. 1) and the I-V protocol (Fig. S5). Because of channel rundown and other time-dependent changes, we recorded first in a reference solution (usually 2 mM Ca²⁺ or 2 mM Ba²⁺), then in a test solution, and finally after return to the reference solution. The effects of one or two different test solutions were examined in each cell. The average of currents in the reference solution (recorded before and after application of the test solution) was used as the control value. For the experiments varying Ca²⁺_o or Ba²⁺_o, rundown was 17 ± 9% (mean ± SD, n = 60), comparing the sum of the absolute values of currents at all voltages from the IIV protocols recorded in the reference solution, before vs. after a test solution. Cells with >40% rundown by that criterion were rejected.

The leak current tended to be nonlinear in “leaky” cells, producing artifactual time-independent outward currents at strongly depolarized voltages (Obejero-Paz et al., 2004). Most cells with >0.2 nA of inward holding current at the holding potential were excluded from analysis. This criterion was relaxed for ∼15% of the cells recorded in 0.1–100 μM Ca²⁺_o or Ba²⁺_o, since the leak tended to be high in that condition, but currents were also large (giving a high signal-to-leak ratio). In such cells, currents inactivated essentially to zero except at the most positive voltages (well above the reversal potential), where the contribution of leak to the measured current was estimated to be <10%.

For a few cells, to reduce 60 Hz noise, a section of baseline (lasting an integral number of 60 Hz cycles, usually 1 or 2) was fitted to a 60 Hz sine wave plus several harmonics (usually 9), adjusting the amplitude and phase for the best fit. The sum of the sine waves was then subtracted from the entire record. This was done with a program written by S.W. Jones in Microsoft Visual Basic v.6.

Effects of ions on permeation were assessed using IIV relations, measured by fitting single exponentials to the decay of current following a brief (2-ms) step to +60 mV (Serrano et al., 2000). The exponential fit began when the tail currents reached a peak, as an estimate of the current at the time when accurate voltage clamp was actually achieved, and extended 20 ms into the voltage steps. The amplitude of the fitted exponential at the starting point of the fit was used for the IIV measurements shown. In most of our experimental conditions, the time course of block is fast, i.e., pore occupancy has reached steady state by the time the IIV is measured. The time course of block can be resolved by careful analysis in certain conditions (1 mM Mg²⁺_o in 2 mM Ba²⁺_o, Serrano et al., 2000; 10 μM Ca²⁺_o, Figs. 7–9), but the single exponential fit did not include those very fast (τ = 0.1–0.2 ms) components, so we interpret the IIV measurements as representing steady-state block in all experimental conditions in this study.

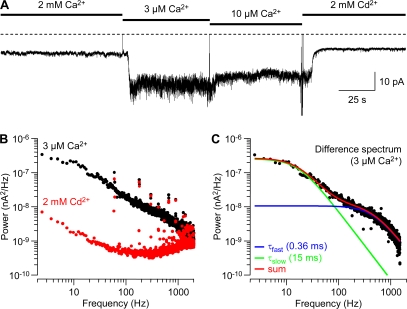
Figure 7.

Noise analysis of block by Ca²⁺_o. (A) “Window” currents at −60 mV in 2 mM, 3 μM, and 10 μM Ca²⁺_o; and in 2 mM Cd²⁺_o. 8-pole analogue Bessel filter at 2 kHz. (B) Averaged power spectra in 3 μM Ca²⁺_o and 2 mM Cd²⁺_o, from ∼60-s records analyzed in 819.2-ms segments, using a Hamming window. (C) The difference between the spectra shown in B, fitted to the sum of two Lorentzian components (440 and 10.5 Hz, corresponding to time constants of 0.36 and 15 ms).

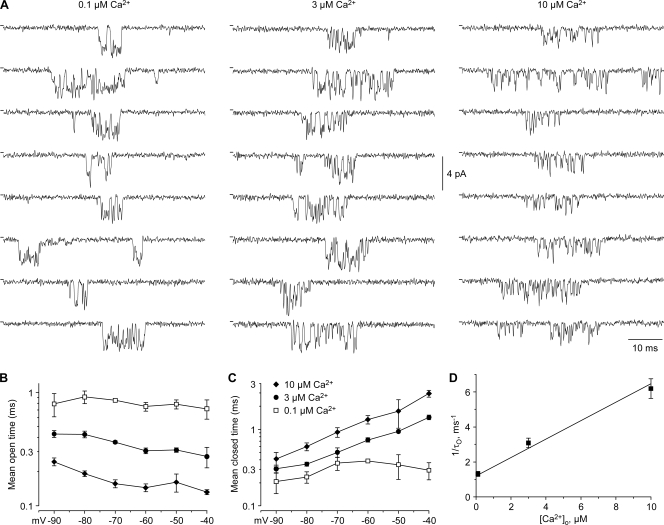
Figure 8.

Single-channel analysis of block by Ca²⁺_o. (A) Bursts of channel activity recorded in the cell-attached configuration, selected from long (5–10 s) depolarizations to −70 mV in 0.1, 3, and 10 μM Ca²⁺_o (n = 3–4). No leak subtraction; tick marks at the left indicate zero pipet current. (B) Mean open times (symbols defined in C). (C) Mean closed times, for the fast component (see Fig. S4, D–F). (D) Dependence of the net closing rate (the reciprocal of the mean open time) on [Ca²⁺]_o. For this analysis, open times from −40 to −90 mV were averaged at each concentration. From a fit to bimolecular kinetics (straight line), the zero-Ca²⁺_o closing rate was 1.2 ms⁻¹, and the blocking rate was 5.3 × 10⁸ M⁻¹s⁻¹. The fit minimized the sum of squared errors for all measured time constants (i.e., it is not a simple linear regression).

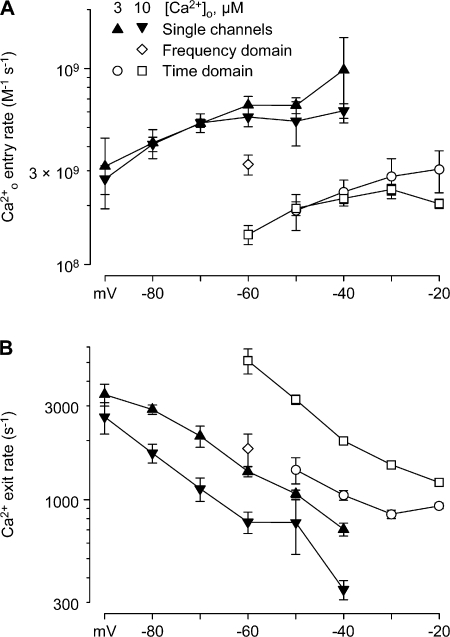
Figure 9.

Rate constants for entry (A) and exit (B) of Ca²⁺, from microscopic and macroscopic data. “Single-channel” rates are reciprocals of closed times (B), or the reciprocal of the open time minus the reciprocal of the open time in 0.1 μM Ca²⁺_o (A), n = 3–4. “Frequency domain” time constants are from the fast corner frequency as in Fig. 7, and the steady-state block (p_B) was estimated from the steady-state currents in 10 μM Ca²⁺_o, divided by the steady-state current in 0.1 μM Ca²⁺_o (assumed to be zero block), n = 3. “Time domain” rates were calculated from time constants (Fig. 6 D) and steady-state block (from Fig. 6 E); n = 9 for 10 μM Ca²⁺_o and n = 3 for 3 μM Ca²⁺_o. For macroscopic data (frequency domain and time domain), rate constants were calculated assuming 1/τ = k_on + k_off, and p_B = k_on/(k_on + k_off); thus k_on = p_B/τ, k_off = 1/τ − k_on. In A, bimolecular rate constants were calculated by dividing k_on by the free Ca²⁺_o. The same symbols were used in A and B.

Chord conductances (G) were calculated from

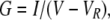(2)

where V_R was estimated by linear interpolation between the two data points on either side of reversal. More sophisticated means of estimating V_R were attempted, including polynomial fits to the IIV relationship (Talavera et al., 2003a,b). However, there were small but systematic differences between the experimental IIV relationship in 2 mM Ca²⁺_o (−150 to +100 mV) and the best fit to even a seventh order polynomial function (not depicted). Small errors in estimation of V_R significantly affected G measurements near V_R.

To minimize error resulting from differences in channel expression levels among cells, measurements were normalized by

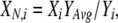(3)

where X_i is a raw measurement from cell i, and X_N,i is the normalized value for that cell. Y is a measure of channel expression level, calculated for each cell (Y_i), and averaged over all cells recorded in the same reference condition (Y_Avg). For IIV currents, Y was the sum of the absolute values of currents from −120 to +100 mV; for conductances, Y was the sum of the corresponding conductance values. One advantage of this procedure is that the “normalized” values have the same units as the raw measurements. Data recorded in the test solution were also normalized using Y values recorded in reference solutions.

The concentration dependence of Ca²⁺ permeation and block was described in terms of chord conductances (G), analyzed as the sum of two components:

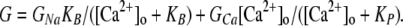(4)

G_Na is the component of conductance that is blocked by Ca²⁺_o, with K_d = K_B, and G_Ca is the component that saturates with increasing Ca²⁺_o, with K_d = K_P. Both components were described by the law of mass action (Eq. 4), except that at the most positive potentials (where no clear increase in G vs. Ca²⁺ was observed at high concentrations) G_Ca was assumed to be constant. Taken literally, this analysis assumes that currents carried by Ca²⁺ and Na⁺ are independent, which is not true for a calcium channel. Therefore, we present this only as a simple way to empirically describe the voltage and concentration dependence of Ca²⁺ permeation and block. Effects of Ba²⁺ were described in the same manner, except that G_Ba was assumed to be constant from +20 to +100 mV.

Analysis of Gating

Effects of ions on gating were determined using the peak currents from the I-V protocol, T_Peak and τ_Inact from the I-V protocol, τ_IIV from the IIV protocol, and channel activation (from the I-V/IIV current ratio, P_O,r) (Serrano et al., 1999).

Peak currents from the I-V protocol were measured following 1 kHz Gaussian filtering, as the average between two cursors placed by eye in Clampfit (Axon Instruments) to delineate the maximal current. Near the reversal potential, cursor placement was based in part on the location of peak inward and outward currents at nearby voltages, with care taken to avoid a fast transient outward gating current (Burgess et al., 2002). Currents and chord conductances were normalized by Eq. 3 to reduce effects of cell–cell variability in expression levels, based on the sum of the absolute value of currents (or conductances, as appropriate) from −90 to +100 mV.

Currents from the I-V protocol were fitted by the sum of two exponentials, from the time where activation was approximately half-maximal, to the end of the 100-ms step, following 2 kHz Gaussian filtering. The slower time constant was defined as τ_Inact, and T_Peak was calculated as the time where the calculated dI/dt = 0. For outward currents, the sum of two exponentials did not fit the peak outward current accurately, but did approximate well the time of peak outward current.

τ_IIV was measured by fitting currents from the IIV protocol to single exponentials, beginning shortly after the peak, and extending to >95% of decay (often to the end of the 100-ms steps).

Channel activation was measured as P_O,r, the ratio of the peak I-V to the IIV (Serrano et al., 1999). Chord conductances calculated from the I-V protocol are often used as a measure of channel activation, but this assumes that the open-channel IIV relationship is linear, which is far from true for T-channels (Fig. 2). On the other hand, the P_O,r is undefined at the reversal potential, and subject to large error nearby. In principle, this singularity can be eliminated by calculating P_O,r from chord conductances rather than currents. However, the additional calculation (dividing by driving force) can increase error as well, so we present P_O,r values from the method that we judge to be most accurate (as noted in figure legends). The maximal P_O,r at strongly depolarized voltages often exceeded 1.0 (in 2 mM Ca²⁺_o, 1.10 ± 0.08, mean ± SD, n = 52), probably because the 2-ms prepulse to +60 mV in the IIV protocol did not precisely match the time of maximal P_O. Therefore, P_O,r values were normalized to the average values from +70 to +100 mV (except in 110 mM Ca²⁺_o or Ba²⁺_o, where those voltages were near the reversal potential and P_O,r was not accurately measurable, so unnormalized values were used).

Figure 2.

IIV relations at different concentrations of Ca²⁺_o (A and B) and Ba²⁺_o (C and D). Values are from 5, 8, 5, 7, 4, and 3 cells in Ca²⁺_o, and 3, 5, 7, 6, 4, and 3 cells in Ba²⁺_o (respectively, 100 nM, 10 μM, 0.1 mM, 0.5 mM, 8 mM, and 110 mM). Control values at 2 mM Ca²⁺_o or Ba²⁺_o are averaged from all these cells (32 in Ca²⁺_o, 28 in Ba²⁺_o). In each cell, the control value was the average of measurements before and after the test solution, to correct for rundown. Values were normalized for each cell as described in Materials and methods. 3–5 are based on this same dataset.

Effects of ions (Ca²⁺_o, Ba²⁺_o, and Mg²⁺_o) on channel gating were analyzed assuming simple parallel shifts along the voltage axis, as predicted (e.g.) by a surface charge mechanism. P_O,r was fitted a Boltzmann relationship raised to the fourth power for each cell, with the slope factor the same in reference and test solutions, using the Solver function in Excel to minimize the sum of squared errors. Log(τ_IIV) was linearly interpolated to the value at 2 ms from data at −70 to −120 mV (see Fig. S7, A and B, and Fig. S15, A and B). Log(T_Peak) was linearly interpolated to the value at 7 ms from data over a 30-mV range (−30 to −60 mV, or more positive voltages in 8 or 110 mM Ca²⁺_o or Ba²⁺_o; see Fig. S7, E and F, and Fig. S15, E and F). This strategy for measuring voltage shifts is similar in principle to Talavera et al. (2003a,b), although the specific measurements differ in detail.

Series Resistance Error

Whole-cell experiments required accurate voltage clamp to control the large currents observed over a wide voltage range. Cells were selected primarily based on the time course and shape of the tail current near −100 mV with the IIV protocol. In some cells, series resistance error was also evaluated from the effect of partial inactivation on the time course of tail currents at −100 mV (Serrano et al., 1999). The average series resistance was 0.75 MΩ (assuming 80% compensation), which would give 16 mV of error for a 21-nA current. This is significant for the largest currents observed in this study, but we note that use of the IIV protocol eliminates the negative slope conductance region normally observed for calcium currents. Series resistance error would selectively underestimate the chord conductance in low Ca²⁺ or Ba²⁺ by ∼13% (calculated for a 16-mV error with 120-mV driving force). The error will be proportionally less for the smaller currents observed with millimolar concentrations of Ca²⁺ or Ba²⁺ (e.g., ∼5% error for the conductance at the most negative voltage in 110 mM Ca²⁺). Put another way, the estimated error was 1% for each 13 nS of conductance. No correction was made for this effect.

For measurement of I-V relations, peak inward currents were <2.5 nA in all conditions (except 100 nM Ca²⁺_o or Ba²⁺_o), so errors should be <2 mV (with 0.75 MΩ of uncompensated series resistance). Errors in T_Peak should also be small, since that value was also measured from inward currents with the I-V protocol. Activation curves were calculated from the I-V/IIV ratio, and the error can be significant for the IIV. In the worst case (100 nM Ca²⁺_o or Ba²⁺_o), at the measured 50% activation voltage (−50 mV), there would be ∼7 mV of error for the IIV. The error would be less than half that value at 10 μM Ca²⁺_o or Ba²⁺_o, and even smaller in all other conditions (e.g., for 110 mM Ca²⁺_o, 2 mV error near half activation). Errors where τ_IIV = 2 ms will be significant (∼15 mV) for the large inward tail currents at 0.1–10 μM Ca²⁺_o or Ba²⁺_o, ∼7 mV in 110 mM Ca²⁺_o, but <5 mV in other conditions. Overall, activation measurements should be reliable (except perhaps at 100 nM), although small shifts (<5 mV) should be interpreted with caution. For the relatively small currents with 2 mM Ca²⁺_o or Ba²⁺_o the estimated errors in our voltage shift measurements are <1 mV, so the small effects in Fig. 12 (C–F) should not be affected by series resistance error (which would be similar in Ca²⁺_o vs. Ba²⁺_o in any case). Voltage shifts shown in the figures are not corrected for series resistance errors.

Figure 12.

Comparison of gating in 2 mM Ca²⁺_o vs. Ba²⁺_o. Values are from all control recordings (n = 52 in Ca²⁺_o, n = 47 in Ba²⁺_o). (A) Effects of Ca²⁺ (▪) and Ba²⁺ (○) on inactivation of inward currents. Time constants were averaged over a 20–30-mV range, centered ∼30 mV negative to the reversal potential (A). (B) I-V relations in 2 mM Ca²⁺_o vs. 2 mM Ba²⁺_o. The same symbols were used in B and D–F (defined in B). Outward currents for the most positive voltage steps (up to +100 mV) are offscale. (C) Voltage shifts, 2 mM Ba²⁺ minus 2 mM Ca²⁺. Experimental values (“Data”) and theoretical values (“Model”) are from the analysis shown in D–F. Voltage shifts were measured as in Fig. 5, for both experimental data and model output. (D) P_O,r in 2 mM Ca²⁺_o or Ba²⁺_o (from Fig. 2, C and D). (E) τ_IIV (from Fig. 3, A and B). (F) T_Peak (from Fig. 3, E and F). Smooth curves in D–F are calculated from a fit to the Serrano et al. (1999) model (see text). Parameter values for Ca²⁺ (named as in Serrano et al., 1999) were k_V = 2521.1 s⁻¹, k_-V = 7.7 s⁻¹, k_O = 3601.1 s⁻¹, k_-O = 23.1 s⁻¹, k_I = 70.1 s⁻¹, k_-I = 1.4 s⁻¹, f = 0.7555, h = 0.0999. k_V, k_-V, and k_-O changed with depolarization e-fold for 24.8062, −17.0591, and −34.114 mV (respectively). Parameters were identical in Ba²⁺, except k_I = 122.5 s⁻¹, thus k_I,Ca/ k_I,Ba = 0.57.

Surface Potential Calculations

Effects of ions on P_O,r were analyzed by Gouy-Chapman theory, i.e., assuming that ions screen but do not bind to a uniform planar surface charge. The measured shift in P_O,r was interpreted as a change in surface potential (ΔΨ). Surface potentials (Ψ) were calculated from the Grahame equation (Grahame, 1947)

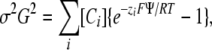(5)

where σ is the surface charge, G is a constant that equals 270 Ųe⁻¹M^0.5 at room temperature, z_i is the valence of the i^th ion species, F is the Faraday constant, and R is the gas law constant. For a given σ value, Eq. 5 was solved for Ψ by a Newton algorithm for each extracellular solution used experimentally, and voltage shifts were calculated as Ψ (test solution) − Ψ (2 mM Ca²⁺ or Ba²⁺). The one free parameter in Gouy-Chapman theory, σ, was found by minimizing the sum of squared differences between experimental and calculated voltage shifts, using the Minimize function of Mathcad.

Frequency Domain Experiments

Stationary noise analysis of whole-cell currents was studied at membrane potentials showing prominent window currents, with 2 mM Ca²⁺_o or with Ca²⁺_o buffered to 0.1, 3, or 10 μM as described above. Currents were sampled at 10 kHz after filtering at 2 kHz with an 8 pole Butterworth filter. The power spectral density was calculated using the fast-Fourier transform routine in Clampfit. Power spectra were averaged from at least 10 records. The spectrum of currents recorded in the presence of 2 mM Cd²⁺ was subtracted from the spectrum recorded without Cd²⁺. The difference spectra were fitted to the sum of Lorentzian functions:

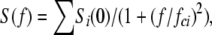(6)

where S_i(0) and f_ci are the zero frequency asymptote and corner frequency of each Lorentzian component. The time constant (τ_i) of each Lorentzian component was

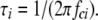(7)

Cell-attached Recording

Single-channel currents were recorded in the cell-attached configuration from HEK293 cells stably transfected with rat Ca_V3.1. The pipet solution contained (in mM) 100 Na, 45 TEA, 3 4-aminopyridine, 1 mM EGTA or HEDTA, 10 HEPES, pH 7.2. The total Ca²⁺ concentration was adjusted as described above to give the desired free concentration (0.1, 3, or 10 μM). The gigaseal was formed in the standard extracellular solution (2 mM Ca²⁺_o; calculated junction potential <1 mV, not corrected). The cell membrane potential was then zeroed with an extracellular solution containing 140 K-aspartate, 0.19 Ca²⁺, 0.62 Mg²⁺, 1 EGTA, 10 HEPES, 10 glucose, pH 7.2. Currents were sampled at 20 kHz after analogue filtering at 5 kHz. Electrodes (2–3 MΩ) were coated with Sylgard and fire polished.

Channel activity was evoked by 5–10-s depolarizations from a holding potential of −120 mV. Patches contained multiple channels, with overlapping openings early in the voltage steps (see Fig. S3), followed by rare isolated bursts as channels transiently recover from inactivation.

Within visually identified bursts, single-channel events were detected by half-amplitude threshold crossing analysis in current records interpolated with eight points between every two sample points (Colquhoun and Sigworth, 1983; Obejero-Paz et al., 1998). Current records were filtered before analysis with a Gaussian filter so the effective cutoff frequency of the combined analogue and digital filters was 2 kHz, with a dead time of 180 μs. The maximum likelihood method was used to fit open and closed time histograms to the sum of exponential functions. We used twice the natural logarithm of the likelihood ratio to assess the number of exponential functions required to fit the distributions (Horn, 1987). Generally, open time distributions were described by a single exponential, and closed times by two exponentials (see Fig. S4). We interpret the fast component of intraburst closed times as closings of a single channel, and do not interpret the slow component.

The single-channel slope conductance was calculated fitting a straight line to the current–voltage relationship of the main conductance level between −90 and −40 mV. Single-channel current amplitudes were calculated by averaging the longest open events (usually ∼20 events) at each membrane potential.

Gating Model

We assessed the effect of Ba²⁺_o on gating of Ca_V3.1 channels using the model of Serrano et al. (1999). Equilibrium state occupancies and transient behavior were calculated analytically by solving the general Q matrix of transition rates between states (Colquhoun and Hawkes, 1995), using the “eigenvecs” and “eigenvals” functions implemented in Mathcad.

A global fit to the voltage dependence of P_O,r, T_Peak, and τ_IIV in 2 mM Ca²⁺ was first performed by finding the model parameters that minimize the sum of squares of scaled differences using the Minimize function implemented in Mathcad. The effective τ_IIV was calculated as the weighted average of the τ's of the three largest components (weighted by the respective amplitudes). In a second step, the voltage dependence of P_O,r, T_Peak, and τ_IIV in Ca²⁺ and Ba²⁺ were fitted simultaneously, allowing only the rate constant for inactivation to change.

General Data Analysis

Data were analyzed using Clampfit v.8.2, Mathcad 2001 Professional (Mathsoft), Microsoft Excel, and Microcal Origin. For the analysis of K_d and G values for permeation and block (Fig. 5), and for Woodhull models for Mg²⁺_o block (Fig. S12, E and F), parameters were estimated by the Solver function of Excel, minimizing the sum of squared errors. Values are given as mean ± SEM unless noted otherwise. Statistical significance levels given in the text are from two-tailed t tests (Excel), with P < 0.05 considered to be significant. For averaged data in the figures, error bars are shown if larger than the symbols. Current records in the figures were digitally Gaussian filtered in Clampfit, with cutoff frequencies specified in figure legends. Figures were prepared in Microsoft PowerPoint, from graphs imported as Windows Metafiles from Origin v. 5.

Online Supplemental Material

The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.200809986/DC1. Fig. S1 compares currents recorded with 3–10 μM Ca²⁺_o buffered by HEDTA, vs. 0–10 μM Ca²⁺_o added to nominally Ca²⁺_o-free solution. Fig. S2 and Table S1 contain results from stationary noise analysis of Ca²⁺_o block. Fig. S3 illustrates the protocol used for single-channel recording, and Fig. S4 shows open and closed time distributions. Fig. S5 illustrates sample current records with the I-V protocol, for different Ca²⁺_o. Fig. S6 compares estimates of channel activation from our P_O,r method vs. chord conductances. Figs. S7 and S8 analyze effects of Ca²⁺_o and Ba²⁺_o on the voltage dependence of gating. Figs. S9 and S10 compare effects of Ca²⁺_o and Ba²⁺_o at equal concentrations. Figs. S11–S18 analyze effects of Mg²⁺_o, and Fig. S19 effects of Mg²⁺_i. Fig. S20 examines replacement of Na⁺_o by NMDG. Fig. S21 compares chord conductances to slope conductances, calculated from IIV relationships. Fig. S22 compares currents evoked by the I-V and IIV protocols at −20 mV, to demonstrate that channel activation is not maximal at that voltage. Figs. S7–S20 are described in the Supplemental Results section. Table S2 (a Microsoft Excel worksheet) includes the data for the Ca²⁺_o, Ba²⁺_o, and Mg²⁺_i,o dependence of currents through the Ca_V3.1 channel, obtained with the IIV protocol.

RESULTS

Effect of Ca²⁺_o and Ba²⁺_o on Permeation

Our approach was to examine the effect of ion concentration on the IIV, using near normal ionic conditions as the reference. Fig. 1 illustrates this for changes to the extremes, 100 nM Ca²⁺_o and 110 mM Ca²⁺_o. It is immediately apparent that inward currents are substantially increased in both test solutions. With 100 nM Ca²⁺_o, outward currents are also increased. This illustrates several well-known features of calcium channel permeation. First, in the near absence of Ca²⁺_o, channels are highly permeable to monovalents (in our conditions, Na⁺). Second, the inward current through calcium channels is not saturated at the physiological concentration (2 mM Ca²⁺_o). Third, Na⁺_i can carry large outward currents, but these outward currents are reduced by 2 or 110 mM Ca²⁺_o. This is consistent with the view that T-type calcium channels, like other calcium channels, are essentially nonselective cation channels in the absence of Ca²⁺_o (Fukushima and Hagiwara, 1985; Carbone and Lux, 1987). Furthermore, Ca²⁺ can either block current carried by monovalent cations, or permeate, depending on voltage and concentration.

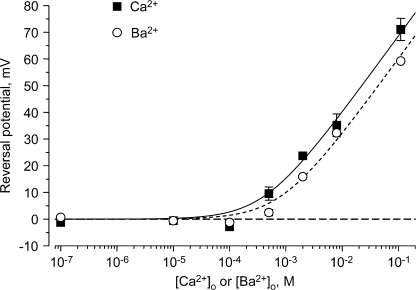
Fig. 2 (A and B) illustrates the effect of Ca²⁺_o on the IIV over a wide (10⁶-fold) range, using normalized IIV relations to correct for rundown and cell–cell variation in expression levels (see Materials and methods). Effects of Ba²⁺_o are qualitatively similar (Fig. 2, C and D). The IIV relations are nonlinear, but monotonic, with voltage. One clear effect is a positive shift in V_R with increasing Ca²⁺_o or Ba²⁺_o (Fig. 3). V_R was near 0 mV at 0.1 mM or lower Ca²⁺_o or Ba²⁺_o, and was more positive with Ca²⁺_o vs. Ba²⁺_o at higher concentrations. The difference in V_R was statistically significant for 0.5, 2, and 110 mM Ba²⁺_o vs. Ca²⁺_o; in a separate set of 3 cells where 8 mM Ba²⁺_o was compared directly to 8 mM Ca²⁺_o, the shift in V_R was 8.3 ± 1.9 mV (P < 0.05). V_R was described reasonably well by Goldman-Hodgkin-Katz theory with P_Ca/P_Na = 87 and P_Ba/P_Na = 44, although V_R in 0.1 mM Ca²⁺_o (−2.8 ± 1.5 mV) and 0.5 mM Ba²⁺_o (+2.5 ± 1.2 mV) was less positive than expected (+2.7 and +6.0 mV, respectively). Above 2 mM, the shift with Ca²⁺_o or Ba²⁺_o approached the Nernstian slope for a divalent cation, both for the calculated Goldman-Hodgkin-Katz (GHK) V_R and for the experimental V_R, although the V_R in Ca²⁺ was ∼100 mV negative to the Nernst potential (Fukushima and Hagiwara, 1985). When activities were used (instead of concentrations), P_Ca/P_Na = 234 and P_Ba/P_Na = 122.

Figure 3.

Effect of Ca²⁺_o and Ba²⁺_o on V_R. Values in 110 mM Ca²⁺_o or Ba²⁺_o are corrected for junction potentials. The smooth curves are the best fits to GHK theory for Ca²⁺_o (solid lines) and Ba²⁺_o (short dashed lines).

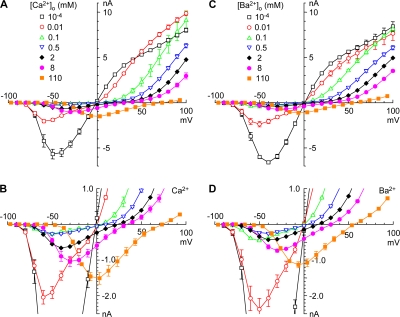
The effects of Ca²⁺_o and Ba²⁺_o on permeation are illustrated more clearly by chord conductance–voltage relationships (Fig. 4), which eliminate the discontinuity in the IIV at V_R (Fig. 2). Consider the effect of increasing Ca²⁺_o from 100 nM to 10 μM (Fig. 4 A). At extreme negative and positive voltages, Ca²⁺_o had little or no effect. However, 10 μM Ca²⁺_o clearly blocked current through calcium channels at intermediate voltages (Fig. 4 C). Qualitatively, this can be explained by a Woodhull (1973) model for voltage-dependent block, where Ca²⁺ rapidly exits to the extracellular solution at positive voltages, or to the intracellular solution at negative voltages. A U-shaped voltage dependence for block by Ca²⁺ has been reported previously for T currents in lymphocytes and sensory neurons (Fukushima and Hagiwara, 1985; Lux et al., 1990). Block was stronger at 0.1–0.5 mM Ca²⁺_o (Fig. 4 C), but still little effect was apparent near +100 mV.

Figure 4.

Chord conductances from IIV relations. (A and B), Ca²⁺_o, (D and E) Ba²⁺_o. (C and F) Block by 0.01–0.5 mM Ca²⁺_o (C) or Ba²⁺_o (F), calculated from the conductance in the indicated concentration divided by the conductance in 100 nM Ca²⁺_o or Ba²⁺_o. Error bars (SEM) include errors in both numerator and divisor, from standard error propagation analysis. Note that these comparisons across datasets yield limiting ratios (at ∼+100 mV) not exactly equal to 1. Same symbols and color coding as Fig. 2.

At millimolar concentrations (Fig. 4 B), Ca²⁺_o increased the conductance at negative voltages, reflecting permeation, but reduced the conductance at the most positive voltages, reflecting block of outward current carried by Na⁺. Again, results in Ba²⁺_o were similar (Fig. 4, D–F).

It is instructive to view conductance both as a function of voltage (with concentration as a parameter; Fig. 4), and as a function of concentration (with voltage as a parameter; Fig. 5, A–D). The smooth curves in Fig. 5 (A–D) are fits to a simple empirical model, where the total conductance is the sum of a component blocked by Ca²⁺, and a component carried by Ca²⁺ (see Materials and methods). Except at the most positive voltages, the chord conductance exhibits a U-shaped voltage dependence, reminiscent of results on the current through L-type calcium channels (Almers and McCleskey, 1984; Hess and Tsien, 1984).

Fig. 5 (E and F) shows the parameters (conductance and K_d values) for the fits to the voltage dependence of chord conductance. The component blocked by Ca²⁺ (“G_Na”) is the extrapolation of the curves shown in Fig. 5 (A–D) to zero Ca²⁺, and the component carried by Ca²⁺ (“G_Ca”) is the extrapolation to saturating Ca²⁺_o. These limiting values are well approximated by the conductances at 100 nM and 110 mM Ca²⁺_o, respectively (see Fig. 5, A–D). G_Na and G_Ca are not true chord conductances for Na⁺ and Ca²⁺ in the sense introduced by Hodgkin and Huxley (1952), since they are components of the chord conductance defined by the observed V_R, not by the equilibrium potentials of Na⁺ and Ca²⁺. Note that G_Ca defined in this way decreases with depolarization, but does not reach zero even at +90 mV. Experimentally, that results from the G-[Ca²⁺]_o curves extrapolating to a limiting nonzero value at high Ca²⁺ (Fig. 5 A).

Fig. 5 F shows the voltage dependence of the apparent K_d values for block and permeation by Ca²⁺_o and Ba²⁺_o. As suggested by Figs. 4 and 5, the K_d for block is strongly voltage dependent. Block was strongest at −30 mV (K_d = 2.8 μM for Ca²⁺_o, 4.0 μM for Ba²⁺_o), and was relieved either by hyperpolarization (K_d = 76 μM for Ca²⁺_o, 101 μM for Ba²⁺_o at −120 mV) or by depolarization (K_d = 2.2 mM for Ca²⁺_o, 3.7 mM for Ba²⁺_o at +90 mV). The K_d for block changed e-fold for 9 mV (Ca²⁺_o) or 11 mV (Ba²⁺_o) with depolarization (+60 to +90 mV), and e-fold for 24 mV (Ca²⁺_o) or 25 mV (Ba²⁺_o) with hyperpolarization (−50 to −120 mV). When the data were fitted using activities rather than concentrations, the voltage dependence was the same, with K_d = 0.9 μM for Ca²⁺_o and 1.2 μM for Ba²⁺_o at −30 mV.

In striking contrast, the apparent K_d for permeation demonstrated little or no voltage dependence from 0 mV to −120 mV (Fig. 5 F). Averaged over that range, the K_d was 3.3 mM for Ca²⁺_o and 2.5 mM for Ba²⁺_o (as activities, 1.1 mM and 0.8 mM, respectively).

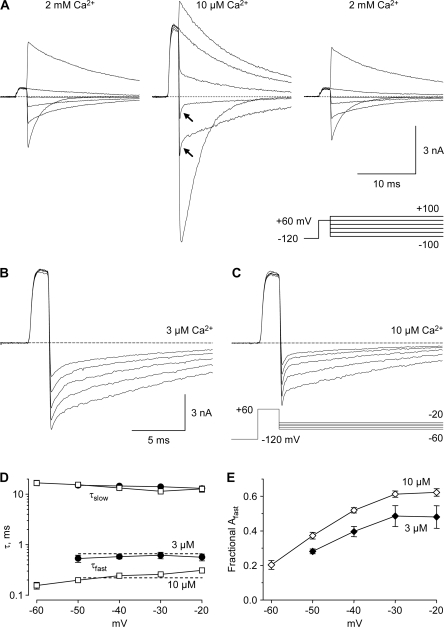
Time-dependent Block by 3–10 μM Ca²⁺_o

Close examination of tail currents recorded in 10 μM Ca²⁺_o revealed a rapid component (Fig. 6 A), possibly resulting from time-dependent block by Ca²⁺_o (Lux et al., 1990). Consistent with that interpretation, tail currents were also biphasic in 3 μM Ca²⁺_o (Fig. 6 B), and the fast component was visibly slower in 3 vs. 10 μM Ca²⁺_o (Fig. 6, B and C). Biexponential fits to the tail currents demonstrated a slow component with τ ∼ 10 ms, which did not depend on Ca²⁺_o, and a concentration-dependent fast component (Fig. 6 D). The simplest explanation is that much of the block by Ca²⁺_o is relieved by strong depolarization (the 2-ms step to +60 mV, Fig. 6 A), and then Ca²⁺_o reenters the pore upon repolarization to voltages where steady-state block is stronger (see Figs. 4 and 5). The fast component does not decay completely to zero, suggesting a rapidly equilibrating but incomplete block, followed by normal tail current kinetics for channels that remain unblocked (at −20 to −60 mV most channels inactivate rather than close; Serrano et al., 1999). If so, the relative amplitude of the fast tail current component reflects the fraction of channels blocked (Fig. 6 E).

Figure 6.

Effect of 3–10 μM Ca²⁺_o on tail current kinetics. (A) Sample records in 2 mM Ca²⁺_o (control and wash, left and right) and 10 μM Ca²⁺_o (middle), shown in 40-mV increments. 3 kHz Gaussian filter. Note biphasic tail currents at −20 and −60 mV (arrows). Tail currents in that voltage range are shown on an expanded time scale for 3 μM Ca²⁺_o (B) and 10 μM Ca²⁺_o (C), from a different cell. (D) Time constants from biexponential fits, from 3 cells in 3 μM Ca²⁺_o (filled circles) and 9 cells in 10 μM Ca²⁺_o (open squares). The dashed lines through the faster time constants are drawn for the 3.3-fold change in time constant expected from bimolecular kinetics. (E) The amplitudes of the fast and slow components to the biexponential fits.

Rapid block by Ca²⁺_o on this time scale (0.1–1 ms; Fig. 6 D) would be expected to produce significant amounts of channel noise. This was examined by stationary noise analysis, exploiting the existence of a “window current” resulting from incomplete inactivation of Ca_V3.1 channels (Serrano et al., 1999). A continuous record of the current at −60 mV over several minutes is shown in Fig. 7 A. Switching from 2 mM Ca²⁺_o to 3–10 μM Ca²⁺_o increased not only the baseline holding current, but also the noise level. The holding current and noise were both reduced by 2 mM Cd²⁺_o, suggesting that the noise results from activity of calcium channels.

Power spectral analysis confirms that the noise is substantially greater in 3 μM Ca²⁺_o than in 2 mM Cd²⁺_o below 1 kHz (Fig. 7 B). The difference spectrum (assuming that the residual noise in Cd²⁺_o reflects sources other than calcium channel activity) could be described by the sum of two Lorentzian components (Fig. 7 C), with corner frequencies corresponding to time constants close to those obtained from biexponential fits to tail currents (Fig. 6 D). Compared with 0.1 μM Ca²⁺_o (where block by Ca²⁺_o should be negligible; Fig. 5), 3–10 μM Ca²⁺_o increased the fractional power in the fast component of the power spectrum (Fig. S2; Table S1, available at http://www.jgp.org/cgi/content/full/jgp.200809986/DC1).

Block by Ca²⁺_o should also affect single channel kinetics, as observed for L-type calcium channels (Lansman et al., 1986). In 0.1 μM Ca²⁺_o, single channel activity could be resolved in cell-attached patches (Fig. 8 A; Fig. S3), with a slope conductance of 33 pS (n = 3; data from −90 to −40 mV), consistent with results on T channels in sensory neurons (Carbone and Lux, 1987; Lux and Carbone, 1987). Channel gating was rapid with many brief flickers and occasional subconductance states. The mean open time was ∼1 ms, and was not clearly voltage dependent from −40 to −80 mV (Figs. 8 B; Fig. S4). In addition to long interburst closed times, mean ≥10 ms, brief closings (mean closed times 0.2–0.3 ms) were also observed (Fig. 8 C).

In patches containing 3–10 μM Ca²⁺_o, bursts of channel activity were observed, including relatively long closed times (Fig. 8 A). The mean open time was reduced by Ca²⁺_o, and was not strongly voltage dependent (Fig. 8 B). In contrast, the faster closed time was longer in 3–10 μM Ca²⁺_o, especially at more depolarized voltages (Fig. 8 C). The dependence of the mean open time on Ca²⁺_o was consistent with block by Ca²⁺ following bimolecular kinetics (Fig. 8 D).

The fast component of closed times observed in 3–10 μM Ca²⁺_o could include both normal closed state(s) (as observed in 0.1 μM Ca²⁺_o) and Ca²⁺ block events. Since the time constants are not very different (Fig. 8 C), we could not reliably resolve multiple fast components. For a closing rate of 1 s⁻¹ (from the mean open time in 0.1 μM Ca²⁺_o), the blocking rate in 3 μM Ca²⁺_o is 2 s⁻¹ (assuming the mean open time in 3 μM Ca²⁺_o is the sum of closing and blocking rates, Fig. 8 D). That predicts that ∼2/3 of the “closed” times in 3 μM Ca²⁺_o are Ca²⁺ block events. Correspondingly, nearly all of the closed times in 10 μM Ca²⁺_o should result from Ca²⁺ block, so those values (Fig. 8 C) should best reflect the true residence time of Ca²⁺ in the pore. Thus, the apparent increase in the faster closed time with Ca²⁺ may reflect a transition from brief Ca²⁺-independent gating events to somewhat slower Ca²⁺ blocking events, rather than an effect of Ca²⁺ on fast gating kinetics.

Fig. 9 compiles estimates of the rate constants for Ca²⁺ entry and exit from three distinct experimental approaches: single channel kinetics, whole-cell noise analysis (“Frequency domain”), and whole-cell tail currents (“Time domain”). Estimates of the Ca²⁺ entry rate (expressed as second-order rate constants) depend little on voltage, and cluster around 3 × 10⁸ M⁻¹s⁻¹ (Fig. 9 A). The rate constant for Ca²⁺ exit is more voltage dependent, e-fold for 26 mV for the single-channel data with 10 μM Ca²⁺ (Fig. 9 B).

The rates estimated from whole-cell tail current kinetics agree qualitatively with the single-channel and noise analysis results, but are approximately twofold slower for entry and approximately twofold faster for exit (especially at 10 μM). These discrepancies are in the direction expected if the initial amplitude of the fast tail current component is underestimated, which is not unexpected for a relaxation with τ ∼ 0.2 ms (Fig. 6 D).

Effects of Ca²⁺_o and Ba²⁺_o on I-V Relations and Activation

The next goal of this study was to determine whether Ca²⁺_o and Ba²⁺_o modify channel gating, in addition to the effects on permeation considered above. We analyzed this by combining information from the I-V protocol (which reflects effects on both gating and on permeation) with the IIV protocol (which isolates effects on permeation). Fig. S5 illustrates sample records obtained with the I-V protocol upon changes in Ca²⁺_o and Ba²⁺_o, and averaged and normalized I-V relations are shown in Fig. 10. In most cases, the peak inward current shifted to more positive voltages as the divalent concentration was increased. However, I-V relations in 10 μM Ca²⁺_o were actually shifted to more negative voltages (compared with 100 nM Ca²⁺_o), opposite to the direction expected from surface charge effects.

Figure 10.

Effects of Ca²⁺_o and Ba²⁺_o on peak I-V relations. Values were averaged and normalized as described in Materials and methods. Ca²⁺_o (A and B) and Ba²⁺_o (C and D) were varied from 100 nM to 110 mM. 10–12 are based on data from the same cells as 2–5. Note that symbol and color coding for different concentrations is the same for Fig. 10 and Fig. 11, A–D.

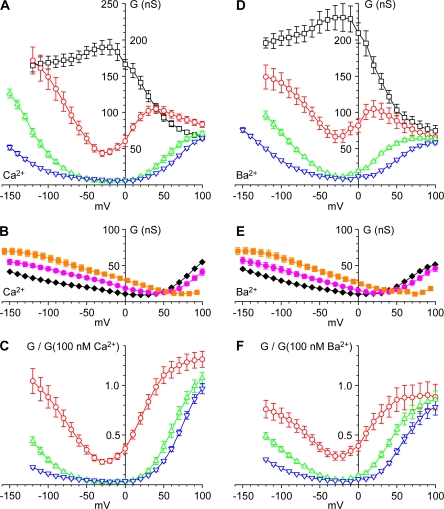
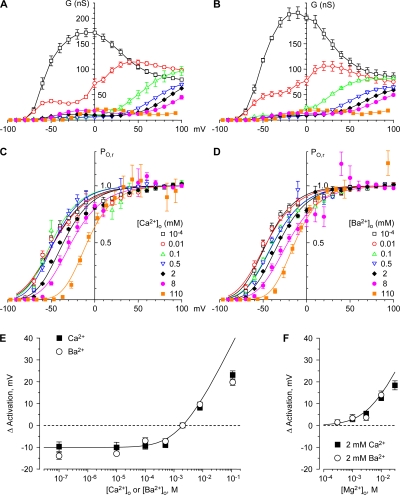
Many studies of calcium channel activation are based on chord conductances, measured from I-V relationships as in Fig. 10. However, the G-V relations are quite complex (Fig. 11, A and B) and do not remotely resemble the Boltzmann relation expected from simple models of channel activation, except in very limited voltage ranges (Fig. S6) (Jones, 2003). The main problem is that G-V is directly related to the extent of channel activation (i.e., open probability) only if the IIV is linear (Hodgkin and Huxley, 1952). For Ca_V3.1, the IIV is distinctly nonlinear under nearly all conditions (Fig. 2), invalidating that assumption.

Figure 11.

Effects of Ca²⁺_o, Ba²⁺_o, and Mg²⁺_o on gating. (A and B) Chord conductances; (C and D) channel activation. Activation was measured as the relative channel open probability (P_O,r) from the I-V/IIV ratio, normalized (see Materials and methods). Smooth curves in C and D are fits to fourth power Boltzmann relationships. (E and F) Shifts in activation with Ca²⁺_o or Ba²⁺_o (E) and Mg²⁺_o (F). Data are from Fig. S8 A (Ca²⁺_o and Ba²⁺_o) and Fig. S16 A (Mg²⁺_o), except that voltage shifts in Ba²⁺_o are defined with respect to 2 mM Ba²⁺_o (not 2 mM Ca²⁺_o). The smooth curve is the fit to Gouy-Chapman theory with a single uniform surface charge density (see Materials and methods).

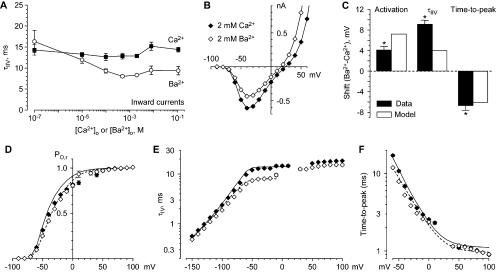
A more direct measure of channel activation is provided by the ratio of the peak current evoked by direct depolarization (as in Fig. 10), divided by the instantaneous current through fully activated channels (Fig. 2). Activation curves calculated by this method are shown in Fig. 11 (C and D). These relationships are also not perfectly described by a simple Boltzmann relationship, likely resulting from the complex macroscopic gating kinetics of Ca_V3.1 channels (Serrano et al., 1999). Fits to Boltzmann relations raised to the fourth power are shown in Fig. 11 (C and D). Although these fits are also not perfect (e.g., they systematically overestimate channel activation at the most negative voltages; Fig. S6, C and D), they are used in this study as an empirical measure of shifts in the voltage dependence of channel activation in different ionic conditions. Qualitatively, activation curves are similar at the lowest Ca²⁺_o (or Ba²⁺_o) concentrations, and shift toward more positive voltages at 2–110 mM. Ca²⁺_o and Ba²⁺_o also shifted other measures of channel gating, including τ_IIV and T_Peak (Supplemental Results; Figs. S7 and S8).

Fit of Activation Shifts to Gouy-Chapman Theory

Fig. 11 E shows a fit of Gouy-Chapman theory to effects of Ca²⁺_o and Ba²⁺_o on the activation curve. Comparable voltage shifts were also observed with Mg²⁺_o (Fig. 11 F; see also Figs. S11–S18). A value of 1 e⁻ per 98 Ų describes most of the data well, although at the highest concentrations the experimentally observed shifts were less than the theoretical curves. If activities were used (instead of concentrations), the best fit was 1 e⁻ per 91 Ų (unpublished data).

Faster Inactivation in Ba²⁺_o, and Effects on Gating Parameters

It has been previously noted that inactivation of Ca_V3.1 is faster in Ba²⁺_o than in Ca²⁺_o (Klugbauer et al., 1999), opposite to expectations for Ca²⁺-dependent inactivation. We find that inward, but not outward, currents inactivate more rapidly in Ba²⁺_o than in Ca²⁺_o (Fig. 12 A; Fig. S7). τ_Inact was 35 ± 2% faster in Ba²⁺_o at 2 mM (for inward currents averaged as in Fig. 12 A; P = 10⁻¹⁷). This analysis allows two novel conclusions. First, outward currents (carried by Na⁺) inactivate more slowly than inward currents in 2–110 mM Ba²⁺_o, comparable to inactivation of outward currents in 2–110 mM Ca²⁺_o, or of inward currents carried by Na⁺_o (100 nM and 10 μM Ca²⁺_o or Ba²⁺_o). Second, the effect of Ba²⁺_o on inactivation of inward currents correlates with block of current carried by Na⁺, since kinetics were intermediate at 10–100 μM Ba²⁺_o; the K_d for block by Ba²⁺_o was 4–5 μM at those voltages. This suggests that the rate of channel inactivation depends on the ion occupying the pore, with Ba²⁺ > Ca²⁺ ∼ Na⁺.

Differences in inactivation rate could appear to affect the voltage dependence of channel activation. Qualitatively, if channels inactivate more rapidly in Ba²⁺_o, fewer channels would be open when peak current is reached, which would decrease the measured channel activation, especially at more negative voltages (where activation is relatively slow). Faster inactivation could also shorten the time to peak current. And to the extent that τ_IIV depends on inactivation, it would be faster in Ba²⁺_o than in Ca²⁺_o. That is, faster inactivation in Ba²⁺_o would produce a downward shift of the activation, τ_IIV, and T_Peak curves, which would appear to be a rightward shift along the voltage axis for activation and τ_IIV, but a leftward shift for time-to-peak (see Fig. 12, D–F). We explored this interpretation by simulating the effect of faster inactivation on these measurements, using the Serrano et al. (1999) model for Ca_V3.1. The model parameters were varied to optimize the fit to the data of Fig. 12 (D–F), with only the microscopic inactivation rate constant allowed to differ between Ca²⁺_o and Ba²⁺_o (see Materials and methods). The fits to the data were not perfect, but it reproduced the key qualitative features (rightward shifts for activation and τ_IIV, leftward shift T_Peak), and the amplitudes of the shifts were reasonably close to the experimental values (Fig. 12 C). We conclude that the subtle differences in gating observed between Ca²⁺_o and Ba²⁺_o result primarily from the more rapid inactivation for inward currents with Ba²⁺_o.

DISCUSSION

We report effects on Ca_V3.1 T-type calcium channels of varying Ca²⁺ and Ba²⁺, over a wide range of concentration (100 nM to 110 mM) and voltage (−150 to +100 mV). One key feature of our experimental design was the use of IIV relations, to isolate effects on permeation from effects on channel gating. This study allows better comparison of ion selectivity in T channels to the classical results on L channels and other HVA calcium channels. In addition, Ca²⁺ and Ba²⁺ affect channel gating, largely as expected for screening surface charge, but pore occupancy by Ba²⁺ also speeds inactivation.

Ca²⁺_o vs. Ba²⁺_o: Permeation

Classically, T-type calcium channels cannot distinguish Ca²⁺ from Ba²⁺, in that inward currents are quite similar for the two ions. We confirm that basic observation (Fig. 2), although careful comparison demonstrates that inward currents are slightly smaller in Ba²⁺_o vs. Ca²⁺_o (Fig. S9). These results dramatically contrast with most HVA calcium channels, where currents are approximately twofold larger for Ba²⁺_o vs. Ca²⁺_o. Furthermore, we find that the pore binds Ca²⁺_o and Ba²⁺_o with similar apparent affinity, either for block of currents carried by Na⁺ or for permeation (Fig. 5 F).

However, some measures of selectivity report larger differences between Ca²⁺ and Ba²⁺. First, V_R was more positive with Ca²⁺_o, consistent with P_Ca/P_Ba = 2 based on GHK theory (Fig. 3). Second, outward currents are larger with 2 mM Ba²⁺_o vs. Ca²⁺_o near +60 mV, demonstrating weaker block of currents carried by Na⁺_i by Ba²⁺_o, although this effect is reduced at more strongly depolarized voltages (Fig. S9). Third, block by Mg²⁺_o is weaker with Ca²⁺_o, as reported previously (Serrano et al., 2000). This effect is also seen for other pore-blocking ions, including Y³⁺ (Obejero-Paz et al., 2004) and Ni²⁺ (Obejero-Paz et al., 2008). We conclude that a T-channel, like an L- or N-channel, can tell the difference between a Ca²⁺_o ion and a Ba²⁺_o ion. However, not all aspects of permeation and block are affected to the same extent by Ca²⁺_o and Ba²⁺_o. This may simply reflect the principle that “affinity” is a poorly defined property for a multiion pore. However, for L channels, the apparent K_d values are lower for Ca²⁺ than for Ba²⁺ for both permeation (Hess et al., 1986) and block (Wang et al., 2005). The selectivity of Ca_V3.1 for Ca²⁺ vs. Ba²⁺ seems to be most apparent when competition among ions is the strongest, e.g., near V_R, or when di- or trivalent pore blockers are present.

We find a GHK P_Ca/P_Ba = 2 (calculated as P_Ca/P_Na divided by P_Ba/P_Na), comparable to previous estimates for T channels (Fukushima and Hagiwara, 1985), but lower than L channels (P_Ca/P_Ba ∼ 4; Lee and Tsien, 1984).

One recent report found no significant difference in V_R between Ca²⁺ and Ba²⁺ for Ca_V3.1, with P_Ba/P_Ca = 0.95 (Shcheglovitov et al., 2007), possibly resulting from difficulty in measuring V_R because of contaminating currents in Xenopus oocytes with high K⁺_i. That study also reported K_d values for permeation by Ca²⁺ (4.2 mM) and Ba²⁺ (5.5 mM) based on analysis of I-V relationships, measurements that could be affected by gating as well as by permeation.

Another recent study found I_Ca/I_Ba = 1.9 at 10 mM (Cens et al., 2007), based on peak currents recorded during voltage ramps. In contrast, using the IIV protocol, we found I_Ca/I_Ba = 1.38 ± 0.02 (G_Ca/G_Ba = 1.24 ± 0.01) at −40 mV in 3 cells where 8 mM Ca²⁺ and Ba²⁺ were compared directly (Fig. S9, G–I). Cens et al. (2007) did not consider effects of Ca²⁺ or Ba²⁺ on gating (which increase Ca²⁺ currents with respect to Ba²⁺), and their results may also be affected by distortion of I-V curves by the use of voltage ramps for rapidly inactivating Ca_V3.1 channels.

Chord Conductance vs. Slope Conductance

Many features of our analysis exploit chord conductances. Historically, most studies on calcium channel permeation simply measured ionic currents, or used slope conductances, primarily because V_R can be difficult to measure for these highly Ca²⁺-selective channels. For Ca_V3.1 channels stably expressed in HEK 293 cells, we have previously demonstrated good current isolation (e. g., by the “envelope test”) over a very wide voltage range (Serrano et al., 1999; Obejero-Paz et al., 2004).

Chord conductances are directly related to ion permeation, by I = G (V − V_R). Chord conductances are always positive, while slope conductances can be negative, e.g. for strongly voltage-dependent block (Adelman and French, 1978). For the nonlinear IIV relationships observed for Ca_V3.1, slope conductances will be systematically larger, and more voltage-dependent, than chord conductances. This effect is small for the relatively linear IIV relationship observed with Na⁺ as charge carrier, but slope conductances are approximately twofold larger than chord conductance at 2 or 110 mM Ca²⁺ or Ba²⁺ (Fig. S21). Block by Mg²⁺ reduces the slope conductance to near zero at voltages and concentrations where block is far from complete (Fig. S21, E and F; compare to Fig. S12, C and D). We do not mean that it is incorrect to use slope conductances as a measure of ion permeation, but it is worth noting that chord and slope conductances can give substantially different numerical values.

Time-dependent Block by Ca²⁺_o

For most conditions in this study ion entry and exit from the pore are rapid with respect to the time course of gating. The exception was 3–10 μM Ca²⁺. From three different experimental approaches (single channel gating, noise analysis of macroscopic currents, and macroscopic tail currents), we estimate that Ca²⁺ blocked Ca_V3.1 channels at a bimolecular rate of 3 × 10⁸ M⁻¹s⁻¹, with little voltage dependence from −20 to −80 mV (Fig. 9). Ca²⁺ blocked whole-cell currents carried by Na⁺ through T channels in sensory neurons at 1.9 × 10⁸ M⁻¹s⁻¹ (Lux et al., 1990), and HVA channels at 1.4 × 10⁸ M⁻¹s⁻¹ (Carbone et al., 1997), although block deviated from bimolecular kinetics at high Ca²⁺ concentrations. Lansman et al. (1986) reported essentially voltage-independent block by Ca²⁺ at 4.5 × 10⁸ M⁻¹s⁻¹ for currents carried by Li⁺ through single L channels, which led to the idea that Ca²⁺ enters open channels at a diffusion-limited rate.

Time-dependent block by Ca²⁺ is visible only in a relatively narrow window of concentration and voltage. For example, the pseudo first-order Ca²⁺ entry rate would be 30 s⁻¹ at 100 nM Ca²⁺_o (slow with respect to channel gating, including inactivation) or 3,000 s⁻¹ at 0.1 mM Ca²⁺_o (not fully resolved by our voltage clamp). Detection of blocking kinetics also depends on the extent of block, which is weak at extreme voltages. We did not see evidence for time-dependent block in tail currents at 10 μM Ba²⁺; possible contributing factors include slightly weaker block by Ba²⁺, and a possible difference in Ba²⁺ entry rate.

Ca²⁺ block has a biphasic voltage dependence, becoming weaker either with strong depolarization or strong hyperpolarization (Fig. 4, C and F; Fig. 5 F). Qualitatively, this agrees with previous results on T channels (Fukushima and Hagiwara, 1985; Lux et al., 1990; Shcheglovitov et al., 2007) and HVA channels (Carbone et al., 1997). From −90 to −20 mV, voltage dependence results primarily from changes in exit rate (Fig. 9). At more depolarized voltages, we do not have separate measurements of entry vs. exit rates for Ca²⁺, but relief of Y³⁺ block by strong depolarization primarily reflected accelerated exit (Obejero-Paz et al., 2004).

Permeation Models and Mechanisms

Our results are consistent with the traditional view that calcium channel selectivity results from ion–ion competition in a single-file pore (Almers and McCleskey, 1984; Hess and Tsien, 1984; Yang et al., 1993), but also with alternative approaches such as Poisson-Nernst-Planck theory (Nonner and Eisenberg, 1998; Boda et al., 2006). The simple models used here, e.g., fitting V_R shifts to GHK theory (Fig. 3), and fitting the concentration dependence of chord conductances to the sum of block and permeation components (Fig. 5), are essentially empirical approaches to data analysis, as opposed to full theories for ion selectivity and permeation. Such analysis can also be applied to current–voltage relationships predicted by a particular quantitative model. We expect that the dataset reported here (Table S2) will be useful to constrain and test future quantitative descriptions of calcium channel permeation.

Measurement of Channel Activation

We also examined effects of Ca²⁺ and Ba²⁺ on channel gating, measuring channel activation as the relative open probability (P_O,r), the ratio of the peak current evoked by the I-V protocol to the maximally activated current (from the IIV protocol). Many studies on calcium channels use chord conductances as a measure of channel activation, but that is valid only if the instantaneous I-V for an open channel is linear. That is clearly not true for Ca_V3.1 (Fig. 2; see also Serrano et al., 1999, 2000). The voltage dependence of chord conductances from the I-V protocol differs dramatically from the expected Boltzmann-like relationship (Fig. 11, A and B). However, the G-V relationship in 2 mM Ca²⁺ is well described by a Boltzmann relationship, if data above −20 mV are not included. Compared with our P_O,r analysis, the V_1/2 is too negative by ∼13 mV, and the steepness of the activation curve is greatly exaggerated (Fig. S6). The “maximal” conductance in that analysis occurs at −20 mV, where a comparison of I-V and IIV protocols clearly demonstrates that channels are not maximally activated (Fig. S22).

The voltage dependence of block can affect voltage shifts measured from the position of peak current with the I-V protocol, or from chord conductances, so such measurements (Shcheglovitov et al., 2007) may not accurately measure shifts in channel gating. Conversely, measurement of fractional inhibition from the I-V protocol (using either currents or conductances) would not accurately estimate the extent of pore block, since that measurement would be affected by both block and by surface charge shifts. For example, measurements from the I-V protocol overestimate the extent of Mg²⁺_o block (and its voltage dependence) at voltages where the activation curve is shifted by Mg²⁺_o (analysis not shown), and the shift in peak inward current (Fig. S14, C and D) greatly exceeds the voltage shift measured using P_O,r (Fig. S16 A).

Channel activation is also shifted by extracellular protons, and the effect of H⁺_o is reduced by divalent cations (Talavera et al., 2003a). That is, reducing the pH from 7.2 (as used in the present study) might shift activation to more negative voltages, especially in low Ca²⁺_o. A differential effect of H⁺_o ions would tend to underestimate the effects of Ca²⁺_o, as measured at pH 7.2. This possibility remains to be evaluated.

Ca²⁺_o vs. Ba²⁺_o: Gating

Although Ca²⁺_o and Ba²⁺_o shifted activation similarly, direct comparison of our three measures of voltage dependence (P_O,r, τ_IIV, T_Peak) in 2 mM Ca²⁺_o vs. Ba²⁺_o showed subtle differences (Fig. 12, C–F). Simulations indicate that these differences can be explained by faster inactivation of inward currents in Ba²⁺_o. Kinetic coupling of activation to inactivation means that changes in either process can appear to affect the other, at the macroscopic level (Talavera and Nilius, 2006). It has long been appreciated that channel “activation curves” do not solely reflect the activation process for a rapidly inactivating channel (Stimers et al., 1985), and the time course of activation (including T_Peak) is also affected by inactivation (Gonoi and Hille, 1987).

The inactivation rate increased with Ba²⁺_o (Fig. 12 A), correlating with the concentration dependence of Ba²⁺_o block of Na⁺ current (Fig. 5, C and D). Therefore, we propose that Ba²⁺ occupancy of the pore speeds inactivation, compared with pores occupied by Na⁺ or Ca²⁺. Although there is ample precedent for effects on gating of pore occupancy by specific ions, it is not clear why Ba²⁺ would have this particular effect.

Surface Charge Effects on Gating of Ca²⁺ and Na⁺ Channels

Activation occurs at more positive voltages in Ca²⁺_o vs. Ba²⁺_o, for both Na⁺ channels (Hille et al., 1975; Ohmori and Yoshii, 1977; Hanck and Sheets, 1992) and HVA Ca²⁺_o channels (Ohmori and Yoshii, 1977; Wilson et al., 1983; Cota and Stefani, 1984; Byerly et al., 1985; Kass and Krafte, 1987; Ganitkevich et al., 1988; Zamponi and Snutch, 1996; Smith et al., 1993). Na⁺ channels also activate at more positive voltages with Ca²⁺_o vs. Mg²⁺_o (Frankenhaeuser and Hodgkin, 1957; Hille et al., 1975; Hanck and Sheets, 1992). It is striking that this is not true for the Ca_V3.1 T-channel, where activation was shifted similarly by Ca²⁺_o, Ba²⁺_o, and Mg²⁺_o (Fig. 11, E and F). Qualitatively, it has been noted previously that Ca_V3 channel activation is comparable between Ca²⁺_o and Ba²⁺_o (Klugbauer et al., 1999; Kaku et al., 2003), but a quantitative comparison of the concentration dependence does not seem to have been reported, and implications for the molecular basis of the surface charge have not been noted.

Why might surface charge effects for Ca_V3 channels differ from both Na⁺ and HVA Ca²⁺ channels? Evolutionarily, based on analysis of conservation of amino acid sequence, Ca_V3 channels are almost equidistant between Na⁺ channels vs. HVA (Ca_V1 and Ca_V2) channels. One known difference is that IQ and EF hand-like domains in the proximal C terminus are conserved among Na⁺ and HVA channels, but absent in Ca_V3. It seems highly unlikely that these intracellular domains are causally related to surface charge effects observed for extracellular cations, but this is a precedent for functional characteristics shared among Na⁺ and HVA channels, but not Ca_V3.

Our data are generally consistent with a classical Gouy-Chapman model, where ions shift channel activation by screening a uniform surface charge. In contrast, the larger voltage shifts with Ca²⁺_o have led to the suggestion that Ca²⁺_o can also bind to the surface charge, i.e., Gouy-Chapman-Stern theory (Hille et al., 1975; Byerly et al., 1985). It now seems abundantly clear that the “surface charge” is specific to a particular channel. For potassium channels, the surface charge may result primarily from charged groups on extracellular domains of the channel protein (Elinder and Arhem, 1999). This remains to be explored for calcium channels.