ARPGE: a computer program to automatically reconstruct the parent grains from electron backscatter diffraction data

A computer program has been written to reconstruct the parent grains from EBSD data of phase transition materials.

Abstract

A computer program called ARPGE written in Python uses the theoretical results generated by the computer program GenOVa to automatically reconstruct the parent grains from electron backscatter diffraction data obtained on phase transition materials with or without residual parent phase. The misorientations between daughter grains are identified with operators, the daughter grains are identified with indexed variants, the orientations of the parent grains are determined, and some statistics on the variants and operators are established. Some examples with martensitic transformations in iron and titanium alloys were treated. Variant selection phenomena were revealed.

1. Introduction

The mechanical properties of many materials, such as steels and titanium alloys, rely on a fine microstructure constituted of lath-shaped micro- or nanometric interconnected daughter grains generated by a phase transformation. Very often the transformation is complete and there is no retained parent phase, or only a very small content. However, knowledge of the parent grains is important in metallurgy. Let us consider one example. During the elaboration of martensitic steels, the impurities migrate at high temperature into the austenitic grains boundaries and, after the martensitic transformation, they form brittle intermetallic particles that are deleterious to the toughness (Cahn et al., 1992 ▶). Moreover, since the prior austenitic grain boundaries are often depleted in chromium, they are also more sensitive to corrosion. Consequently, the size of the prior austenitic grains is a key microstructural parameter in the mechanical models of martensitic steels. Knowledge of possible variant selection is also important in metallurgy and this phenomenon must be controlled in order to optimize the texture by thermo-mechanical treatments. For instance, in shape memory alloys, the mechanical properties come from variant selection during deformation or heating treatment (see, for example, Kaouache et al., 2006 ▶). Generally speaking, there is an important need in the metallurgical community to have a computer program that automatically reconstructs the parent grains and establishes statistics on the variant selection.

Electron backscatter diffraction (EBSD) is a technique used in scanning electron microscopy that allows phase identification and orientation mapping with an angular resolution of ∼1° and a spatial resolution of ∼10 nm. We have recently developed a method based on a general crystallographic theory (Cayron, 2006 ▶) to automatically reconstruct the parent grains from EBSD data of materials constituted only of daughter grains (Cayron et al., 2006 ▶). The aim of the present paper is to present a computer program called ARPGE, for automatic reconstruction of parent grains from EBSD data, which uses this method and integrates new functionalities. It reconstructs the parent grains, determines their orientation and texture, identifies the variants, and establishes some statistics that can help to understand the variant selection mechanisms. The software treats any structural phase transformation materials.

2. Description of the program

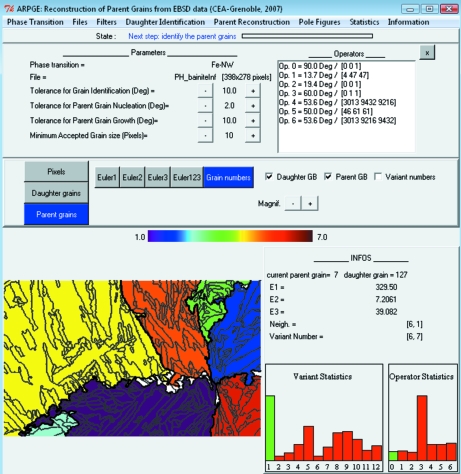
ARPGE has been written in Python, which is a multi-platform, interpreted and object-oriented language (Martelli, 2006 ▶; see also http://www.python.org/). The main menu of ARPGE, presented in Fig. 1 ▶, is constructed using the graphical user interface library TkInter. The program needs the following.

Figure 1.

Main menu of the ARPGE program with, for example, some austenitic grains reconstructed in a bainitic steel.

(i) The phase transformation data, i.e. the parent and daughter point groups, the orientation relationship, and the resulting theoretical groupoid composition table generated by the computer program GenOVa (Cayron, 2007 ▶). These data can be imported or created from the ‘Phase Transition’ menu.

(ii) The experimental EBSD map acquired with commercial EBSD equipment such as HKL or TSL and imported in the ‘Files’ menu.

The ‘Filters’ menu allows removal of ‘spikes’ (indexation errors) and dilation of the pixels to remove badly indexed areas. The ‘Daughter Identification’ menu allows us to identify the daughter grains according to a criterion on the misorientation angle (‘Tolerance for Grain Identification’) and to a criterion on the minimum number of pixels per grain (‘Minimum Accepted Grain size’). This reconstruction is performed in two steps, firstly by comparing only the Euler angles (leading to pre-grains) and secondly by checking if the misorientations between the pre-grains are close to a symmetry operation. This part of the program is not optimized and the calculations are quite long in comparison with commercial software. The new and optimized part is the ‘Parent Reconstruction’ menu. The program checks if the misorientations between neighboring daughter grains are close to the theoretical operators and, if the result is positive, it checks if the composition of these operators is in agreement with the theoretical groupoid composition table. This parent grain reconstruction is performed in two steps: a nucleation step with a low tolerance angle (usually 3–5°) and a growth step with a larger tolerance angle (usually 10–15°). These two angular parameters, ‘Tolerance for Parent Grain Nucleation’ and ‘Tolerance for Parent Grain Growth’, are the only parameters needed for the reconstruction. The details are reported by Cayron et al. (2006 ▶), but now the ‘tolerated misindexation’ parameter is not needed. The reconstruction is saved automatically and, if it is not complete, the user can continue the process by increasing the two tolerance angles. In general, one or two cycles are enough to reconstruct more than 80% of the map. The calculations are quite fast because they rely on comparison of integers and there is no need to solve any equation. For example, on a 1.5 GHz computer with 500 Mb RAM, it takes 10 min for a steel constituted of 100 martensitic grains reconstructed into six austenitic grains, and 1 h for a similar steel containing 1000 martensitic grains reconstructed into 100 austenitic grains.

In addition to the work of Cayron et al. (2006 ▶), ARPGE now integrates new possibilities. The variant indices are automatically calculated and can be seen in the map. These indices are integers between 1 and the number of variants. The number 1 is attributed to the largest daughter grain encountered during the nucleation step. The orientations of the parent grains are automatically determined and can be visualized with the ‘Pole Figures’ menu on stereographic or equal-area pole figures simply by double-clicking on the parent grains in the map. Special misorientations between the parent grains, such as Σ3 twins, can be determined. The global pole figure corresponding to the texture of the parent grains can also be drawn. In the ‘Statistics’ menu, the indices of variants and operators are represented on charts that allow us to see at first glance a possible variant selection phenomenon. The reconstructed parent data can be exported to files compatible with commercial computer programs.

3. Some examples

3.1. Bainitic/martensitic irons and steels

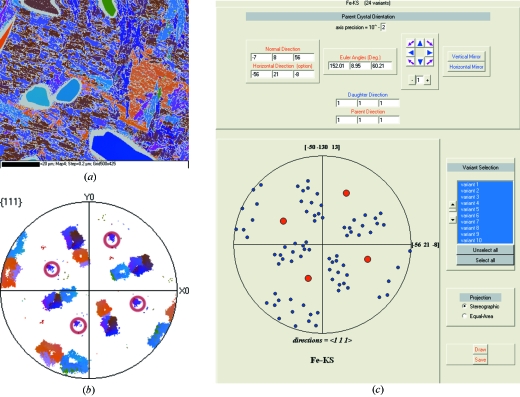
The first example is a martensitic iron from a meteorite (courtesy of J. Michael, Sandia National Laboratories, USA). The EBSD map has been acquired by detecting only the martensitic phase, i.e. the body-centered cubic (b.c.c.) structure. The austenitic phase, i.e. the face-centered cubic (f.c.c.) structure, was not considered at all. The orientations of the different martensitic grains are coded by colors representing the Euler angles and illustrated in the orientation map of Fig. 2 ▶(a) and in the associated pole figure (Fig. 2 ▶ b). ARPGE finds only one austenitic grain, whose orientation is indicated by the red circles superimposed on the pole figure (Fig. 2 ▶ b). One can check that this calculated orientation is the correct one by comparing the experimental pole figure (Fig. 2 ▶ b) of the martensitic grains with the theoretical pole figure simulated with the GenOVa program and reported in Fig. 2 ▶(c). One may also notice that the red circles corresponding to the calculated austenite orientation coincide with some experimental directions attributed to the martensite phase. The martensitic directions are not present in the theoretical simulation of Fig. 2(c) ▶. This is a result of a misindexation between the austenite and the martensite phases during the EBSD acquisition.1 Therefore, the coincidence between the reconstructed red circles and these experimental directions can be considered as another proof for the efficiency of the reconstruction.

Figure 2.

A martensitic iron (courtesy of J. Michael). (a) EBSD orientation map of the martensitic grains and (b) corresponding pole figure. ARPGE finds only one austenitic grain, whose orientation is indicated by the red circles superimposed on the pole figure. (c) According to that orientation, theoretical pole figure of the 24 variants (blue spots) in a Kurdjumov–Sachs orientation relationship with the parent crystal (red spots).

The second example is a bainitic steel (courtesy of P. H. Jouneau, INSA-Lyon, France). Since the proportion of residual austenite is more important in that material, both bainite (b.c.c.) and austenite (f.c.c.) phases have been taken into consideration during the EBSD acquisition. The quality map is presented in Fig. 3 ▶(a). The orientation of the retained austenite is given in Fig. 3 ▶(b). We then tested ARPGE to check if it could effectively find the austenitic grains and their orientations only from the bainitic data. Only the experimental bainitic orientations were loaded into the ARPGE program. Assuming a bainitic transformation with a Nishiyama–Wasserman (NW) orientation relationship, ARPGE finds six austenitic grains, represented in Fig. 3 ▶(c). Their orientations are given by the red spots in the pole figures. The experimental orientations of the retained austenite corresponding to these reconstructed areas are reported in Fig. 3 ▶(d). In that figure, we have also superimposed the calculated austenitic orientations of Fig. 3 ▶(c) by using red circles. All the experimental austenitic orientations are located inside the calculated red circles. This proves the efficiency and the high precision of the reconstruction algorithms used in ARPGE. Nevertheless, some other orientations have not been detected [blue arrows in Fig. 3 ▶(d) and other small dots]. These orientations correspond to twins of the austenitic grains 1, 3, 4 and 6 and also to bainite wrongly indexed as austenite (see footnote 1). By a careful examination of the data, we have concluded that the twins could not have been found because they have generated only ‘common’ variants. Let us explain. We have proved in §9.2 of Cayron (2006 ▶) that, assuming an NW orientation relationship, four variants are always sufficient to reconstruct without ambiguity the orientation of the austenitic crystal, and we have shown that an austenitic crystal can share three common bainitic variants with its Σ3 twin. These common variants are those encountered in the case of Fig. 3 ▶. We believe that the presence of only these common variants in the twinned austenite is not a coincidence but results from stress accommodation mechanisms during the bainitic transformation. Such a hypothesis would need deeper study. This example shows the intrinsic limit of our reconstruction program; there is no method based only on orientation measurements that allows the distinction between untwinned and twinned austenite if the twinning process generates only the three common variants.

Figure 3.

Bainitic steel (courtesy of P. H. Jouneau). (a) Quality index map. (b) Orientation map of the austenite phase. (c) ARPGE finds six austenitic grains (only the information on the bainitic phase has been taken into account in the reconstruction). The experimental orientations of the bainitic grains inside the reconstructed austenitic grains and the calculated orientations of the austenitic grains are represented by the 〈111〉 directions in the pole figures by blue and red spots, respectively. (d) The experimental orientations of the residual austenite corresponding to the six reconstructed grains are reported and the calculated orientations are superimposed with red circles. One may check the perfect agreement between the calculated and the experimental orientations of the austenitic grains. The other spots come from twinned austenite (blue arrows) and some bainitic grains misindexed as austenite.

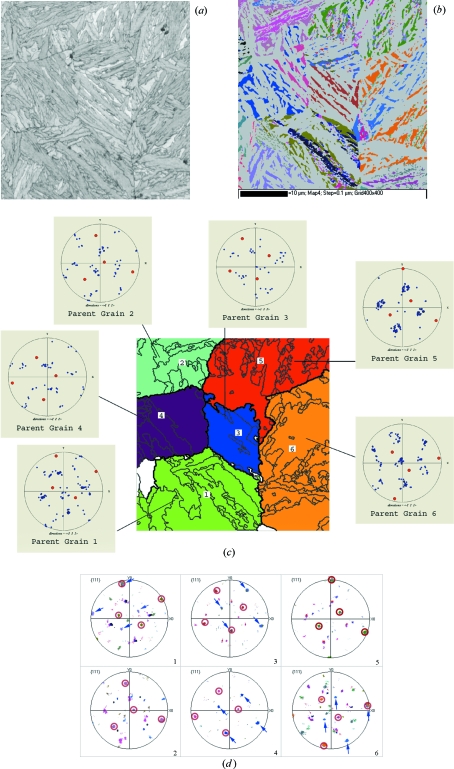
The third example is a martensitic steel used in nuclear pressured water reactors (courtesy of J. M. Gentzbittel, CEA-Grenoble, France). There is absolutely no residual austenite. The EBSD orientation map of the martensite is given in Fig. 4 ▶(a); the reconstructed austenite is presented in Fig. 4 ▶(b). More than 100 austenitic grains could be identified and their orientation determined. Some examples of the pole figures of the reconstructed austenitic grains are presented in Fig. 4 ▶(c). The reconstruction works even for small austenitic grains containing few martensitic grains (see grain 39 for example). The number of austenitic grains is enough to establish some statistics on the variant and operator indices, as illustrated in Fig. 4 ▶(d). The variant α₁ is the most frequent because the programs always choose the index 1 for the larger grain during the nucleation process. In future versions of ARPGE we could attribute a random index between 1 and the theoretical number of variants to suppress this effect. It may be noticed that the most frequent operator is O₃. This is a clear example of a variant selection phenomenon. Actually, this is not a surprise. The operator O₃ corresponds to a rotation of 60° around the [110]_α = [111]_γ direction (Cayron et al., 2006 ▶); it links the three variants that share a common (111)_γ plane (these three variants are also the ‘common’ variants for twinned austenite). The fact that the most frequent variants after the variant α₁ are the variants α₅ and α₉ results from the high frequency of operator 3 (material property), the high frequency of the variant α₁ (algorithm effect) and the fact that operator O₃ contains the arrows α₁₅ and α₁₉ (theory).

Figure 4.

Martensitic steel (courtesy of J. M. Gentzbittel). (a) Orientation map of the martensite. (b) Reconstructed austenite (the boundaries of the martensitic grains are not shown here for better visibility). (c) Pole figures of some of the reconstructed austenitic grains with their calculated orientations (red spots) and with the experimental orientations of the martensitic grains (blue spots). (d) Statistical bar charts on the distributions of the variant indices and operator indices (the percentages of encountered variants or operators are given as a function of their indices).

3.2. Titanium alloys

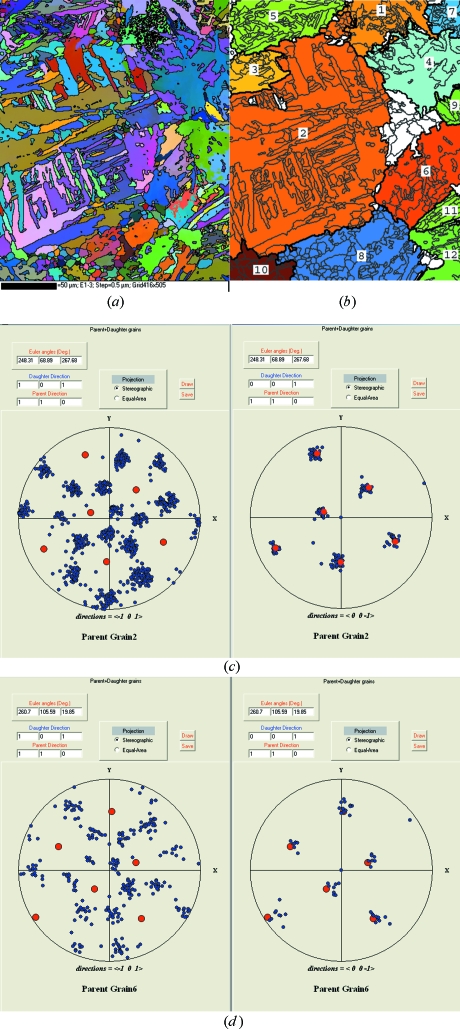
ARPGE has been written to work with any structural phase transition. We have checked, for instance, its performance for the Burgers transition where the parent cubic β phase is transformed into the daughter hexagonal α phase. The first example is a wrought titanium Ti-6Al-4V alloy used in the Vulcain engine of the Ariane 5 rocket. The EBSD orientation map of the α grains is given in Fig. 5 ▶(a), and the reconstructed parent β grains are presented in Fig. 5 ▶(b). Pole figures of two reconstructed grains are presented in Figs. 5 ▶(c) and 5 ▶(d). It can be seen that the calculated 〈110〉_β directions coincide with the experimental 〈001〉_α directions, in agreement with the Burgers orientation relationship. Moreover, the patterns formed by the α grains coincide with the theoretical GenOVa simulations (not presented here). The reconstruction took 10 min.

Figure 5.

Wrought titanium Ti-6Al-4V alloy. (a) EBSD orientation map of the α grains. (b) Reconstructed parent β grains. Pole figures of (c) grain 2 and (d) grain 6 with the projection of the 〈101〉_α directions (on the left) and 〈001〉_α directions (on the right).

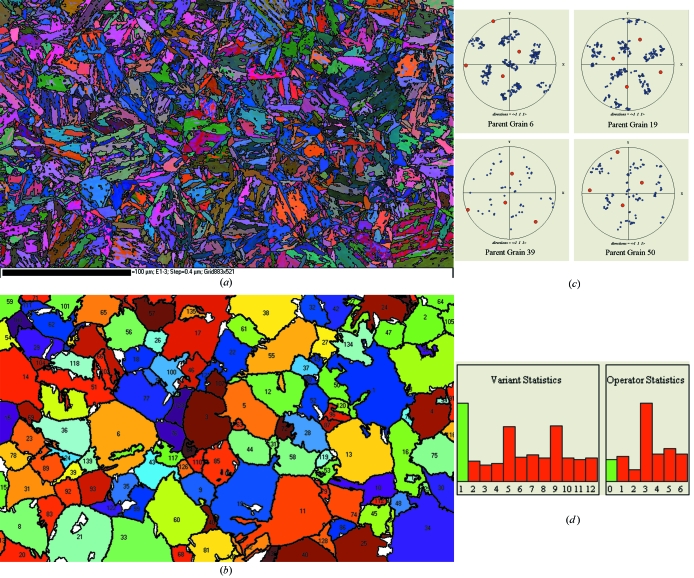
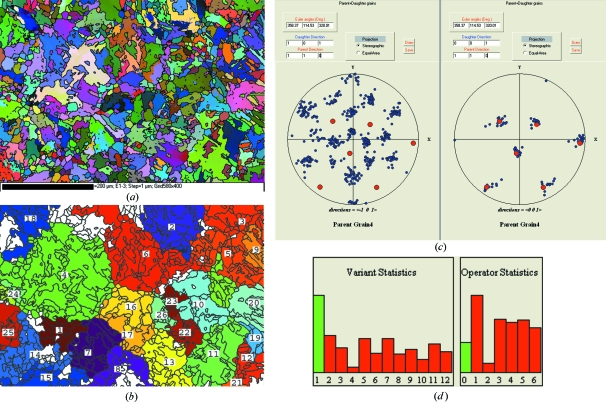
The last example is a Ti-6Al-4V titanium alloy elaborated by powder metallurgy and studied for the future engine Vinci of the Ariane 5 rocket. The EBSD orientation map of the α grains is given in Fig. 6 ▶(a), and the reconstructed parent β grains are presented in Fig. 6 ▶(b). Despite the presence of small highly deformed and dis­oriented α grains, the reconstruction seems to be correct. For example, one may check on the pole figure (Fig. 6 ▶ c) of the largest reconstructed grain that, here again, the calculated 〈110〉_β directions coincide with the experimental 〈001〉_α directions, in agreement with the Burgers orientation relationship. The reconstruction lasted 30 min. One may also notice in the statistics presented in Fig. 6 ▶(d) that the operator O₁ is the most frequent and that operator O₂ is nearly absent. This result is quite surprising. One would have expected to find a high proportion of operator O₂ because this operator corresponds to a rotation of 10.5° around the hexagonal c axis, i.e. the misorientation between the two variants that share a common (110)_β plane (see Table 4 of Cayron, 2006 ▶). A global understanding including the shape of the variants and the elastic field in the set of variants could probably explain such a feature.

Figure 6.

Powder metallurgy Ti-6Al-4V titanium alloy. (a) EBSD orientation map of the α grains. (b) Reconstructed parent β grains. (c) Pole figures of grain 4 with the projection of the 〈101〉_α and 〈001〉_α directions. (d) Statistical bar charts on the variant and operator indices.

4. Conclusions and perspectives

ARPGE is a program that reconstructs the parent grains from the data obtained on the EBSD maps of phase transition materials. There is no need for any retained parent phase. The program works for any structural phase transformation. We have checked its validity for martensitic and bainitic transitions in irons and steels and for Burgers transitions in titanium alloys. The first menus (‘Files’, ‘Filters’ and ‘Daughter Identification’) are the same, although less optimized and effective, as those of commercial EBSD software. The other menus are new. The principle of the method relies on checking the coherence of the operator composition (Cayron et al., 2006 ▶). The parent grains are reconstructed, their orientation calculated and the daughter grains are identified with indexed variants. Some statistical charts on the variant and operator indices are established. Variant selection phenomena can be easily visualized on these charts.