Abstract
To improve tertiary structure predictions of more difficult targets, the next generation of TASSER, TASSER_2.0, has been developed. TASSER_2.0 incorporates more accurate side-chain contact restraint predictions from a new approach, the composite-sequence method, based on consensus restraints generated by an improved threading algorithm, PROSPECTOR_3.5, which uses computationally evolved and wild-type template sequences as input. TASSER_2.0 was tested on a large-scale, benchmark set of 2591 nonhomologous, single domain proteins ≤200 residues that cover the Protein Data Bank at 35% pairwise sequence identity. Compared with the average fraction of accurately predicted side-chain contacts of 0.37 using PROSPECTOR_3.5 with wild-type template sequences, the average accuracy of the composite-sequence method increases to 0.60. The resulting TASSER_2.0 models are closer to their native structures, with an average root mean-square deviation of 4.99 Å compared to the 5.31 Å result of TASSER. Defining a successful prediction as a model with a root mean-square deviation to native <6.5 Å, the success rate of TASSER_2.0 (TASSER) for Medium targets (targets with good templates/poor alignments) is 74.3% (64.7%) and 40.8% (35.5%) for the Hard targets (incorrect templates/alignments). For Easy targets (good templates/alignments), the success rate slightly increases from 86.3% to 88.4%.
INTRODUCTION
Despite several decades of intense effort, the ability to predict the native structure of a protein from its amino acid sequence has not been fully achieved (1–4); nevertheless, three general approaches to protein structure prediction have been developed: comparative modeling (5–8), threading (9–11), and template-free methods (12–15). The basic ideas of comparative modeling and threading are identical, viz. identify a set of template proteins whose structure is related to the target sequence. To find such structurally related templates, comparative modeling relies on the evolutionary relationship between the target and template sequences (16), whereas threading aims to identify template proteins having a similar fold as the target sequence, irrespective of their evolutionary relationship (17). Essential to the success of any comparative modeling and threading method is the requirement that the Protein Data Bank (PDB) (18) contains structures related to that adopted by the target sequence. On the other hand, template-free methods are designed to predict the three-dimensional native structure of a protein without a priori knowledge of the structure that the target will adopt. Although in principle it is the most general approach, in practice, it is the least reliable (19).
Over the past several years, improvement in fold recognition algorithms that has enabled the identification of correct, but evolutionarily distantly related templates as well as the increase in the number of solved protein structures in the PDB, have made comparative modeling and threading the most successful prediction approaches (10,20). In addition, there are several studies that find that the current PDB library is complete because it can provide accurate templates for all compact single domain proteins (21–24). At least for individual domains, the prediction problem for the single domain proteins could be solved by the current PDB library if there were fold recognition tools that could recognize these correct templates and generate good alignments (25). However, for ∼1/3 of proteins that are weakly/nonhomologous to proteins in the PDB, this is not yet possible (26).
The recently developed protein structure prediction algorithm TASSER and its variants have shown a reasonable level of success for targets that are weakly or nonhomologous to templates in the PDB (26–31); have provided significant improvement over initial template alignments in comprehensive PDB benchmarking (28,29,32); have been applied to the structure prediction of identified all human G protein-coupled receptors (33), with encouraging results shown for the prediction of the tertiary structure of the β-adrenergic G protein-coupled receptor structure that was recently solved (34,35) (J. Skolnick, unpublished); and was among the top ranked algorithms in CASP7 (26,28,31,33,36). The original version of TASSER (26) takes the initial template alignments and predicted side-chain contact restraints provided by the threading algorithm, PROSPECTOR_3 (37), and then refines the structures from these initial templates. The overall performance of TASSER is quite dependent on the accuracy of the predicted side-chain contacts. In previous work, comprehensive benchmarking showed that TASSER can fold ∼2/3 of all non- or weakly homologous proteins ≤200 residues in length (26,36). Moreover, the resulting TASSER models were closer to the native structures than the initial threading templates. For the remaining ∼1/3 of proteins, the prediction accuracy of TASSER is significantly worse because PROSPECTOR_3 provides inaccurate template fragments and predicted side-chain contact restraints. Thus, improvement in this regime of target difficulty is sorely needed.
In this work, to improve the accuracy of the predicted contact restraints, we develop what to our knowledge is a new side-chain contact restraint prediction algorithm, the composite-sequence method, and incorporate this information into the next generation of TASSER, TASSER_2.0. The basic idea of the composite-sequence method is to generate predicted side-chain contacts by a number of approaches, and then obtain the consensus set of contacts with the expectation that these will be more accurate than any of the individual input sets. To generate one of these sets of predicted contacts, we evolve sequences optimized for each template structure using a structure-based scoring function that contains secondary structure, burial, and pair interaction potentials. The resulting set of sequences is used to generate sequence profiles used in an improved version of threading, PROSPECTOR_3.5. Then, by using consensus contacts extracted from the evolved-sequence method and those obtained from wild-type template sequences, the composite-sequence method, we find that there is a significant improvement in contact prediction accuracy. Yet, the coverage is sufficient that these more accurate contacts can be effectively used in TASSER_2.0. We apply TASSER_2.0 to a comprehensive, large-scale benchmark test set consisting of 2591 nonhomologous single domain proteins having ≤200 residues of which 772, 513, and 1306 are all α-, all β-, and α/β-proteins. In this benchmark, no template can have >30% sequence identity to the target sequence. (The list of 2591 single domain benchmark proteins is prepared as Supplementary Material, Data S1.) We compare the performance of TASSER_2.0 with the original TASSER algorithm and demonstrate significant improvement, especially for the more difficult targets.
METHOD
The original version of TASSER consists of template identification and side-chain contact restraint prediction by the threading algorithm PROSPECTOR_3, followed by structure assembly and final model selection (26). To generate more accurate predicted contact restraints, we develop the composite-sequence method that provides the more accurate predicted contact restraints to TASSER_2.0. TASSER_2.0 employs an additional contact restraint energy function to increase the influence of these more accurate contacts, but uses the same procedure for structure assembly and final model selection as TASSER. Since detailed descriptions of TASSER are available elsewhere (25,26,28), we just provide a brief overview.
Synthetic evolution of template sequences
For each template in the threading template library, we independently evolve a set of 80 sequences designed to minimize the energy of the sequence in its native template structure. For a given sequence, the energy is given by
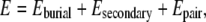 |
(1a) |
where
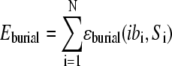 |
(1b) |
is a centrosymmetric, residue-dependent statistical burial potential (38), where the protein is divided into spherical shells of width equal to 1/3 the radius of gyration of the side-chain centers of mass (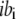 = 1,5), and
= 1,5), and 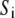 is the amino acid at position i = 1,N, with N the number of residues in the protein chain. The secondary structure potential is given by
is the amino acid at position i = 1,N, with N the number of residues in the protein chain. The secondary structure potential is given by
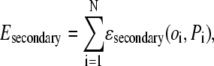 |
(1c) |
where oi (Pi) is the observed (predicted) secondary structure (helix, β, coil) of residue i. If oi = Pi, then
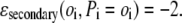 |
(1d) |
Otherwise,
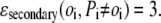 |
(1e) |
The secondary structure is predicted using a neural network-based approach that is logically the same as PSIPRED (39), but is designed to work on a single sequence (H. Zhou, unpublished). The approach was tested on a set of 820 nonhomologous sequences and has an average accuracy of 67%. Our purpose here is not to generate yet another neural network-based approach to secondary structure prediction, but to have one that is applicable for a single sequence rather than one that requires a multiple sequence alignment.
The pair potential is given by
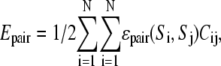 |
(1f) |
where 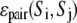 is a previously derived, orientation-independent, knowledge-based pair potential between amino acids
is a previously derived, orientation-independent, knowledge-based pair potential between amino acids 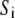 and
and 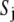 (40), and Cij = 1 if side chains i and j are in contact (a pair of side chains is in contact if any pair of their heavy atoms is within 4.5 Å) and Cij = 0 otherwise and is taken from the template structure and remains unchanged during the sequence evolution procedure.
(40), and Cij = 1 if side chains i and j are in contact (a pair of side chains is in contact if any pair of their heavy atoms is within 4.5 Å) and Cij = 0 otherwise and is taken from the template structure and remains unchanged during the sequence evolution procedure.
In practice, we start with the native sequence and using a genetic algorithm, evolve it to minimize the potential given by Eq. 1. The population consists of 75 members and is evolved for 500 generations. In each generation, each of the 75 sequences is randomly permuted (thus, the amino acid composition always matches the native sequence), and the 75 lowest energy sequences among the 75 parents and 75 children are selected. The set of sequences is evolved for 500 generations, after which the lowest energy sequence is stored. A total of 80 independently generated sequences are then collected. For the template library, the average sequence identity of the evolved sequences to the native sequence is 63%, with a standard deviation of 5%.
PROSPECTOR_3.5 algorithm
As described for PROSPECTOR_3 (9,37), PROSPECTOR_3.5 uses a set of four scoring functions and multiple iterations. Here, we first summarize the essential features and subsequent modifications in the original sequence profile scoring function utilized in the current version, PROSPECTOR_3.5, and then describe modifications to accommodate the evolved sequences whose generation was described in the previous section.
First pass using sequence profiles and secondary structure terms
In what follows, upper (lower) case characters I, J, (i,j) refer to the residue index in the target (template) structure, and jk refers to template structure number jk. The initial alignment uses a scoring function between target sequence residue I and template sequence j in template jk of the type (10,41)
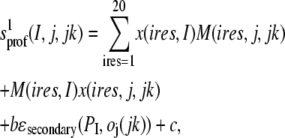 |
(2a) |
where the sum is over amino acid types, x(ires,I) (x(ires,j,jk)) is the fraction of residues of type ires at position I (j) in the target (template), and M(ires,I) is the corresponding PSI-BLAST MTX profile (42,43). 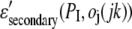 is the secondary structure energy for predicted secondary structure type, PI, and observed secondary structure,
is the secondary structure energy for predicted secondary structure type, PI, and observed secondary structure, 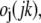 of residue j in template jk. Since we consider better scores to be more positive (as opposed to the previous section, where better energies are more negative),
of residue j in template jk. Since we consider better scores to be more positive (as opposed to the previous section, where better energies are more negative),
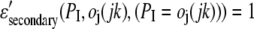 |
(2b) |
and
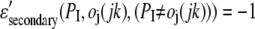 |
(2c) |
otherwise. b and c are constants that depend on the type of sequence profile used.
In the original formulation of PROSPECTOR_3 (37), we used two sets of sequence profiles: Those that are derived for all sets of sequences having between 35% and 90% pairwise sequence identity, the 3590 set (in Eq. 2a prof = 3 590), and those whose e value to the parent (target or template) sequence is ≤10, the e10 set (in Eq. 2a prof = e10). In all cases, the MTX profiles are those derived from the 3590 set of sequences. For the 3590 (e10) set, b = 0.7 (0.8) and c = 1.5(1.3).
We first generate a target-template sequence alignment using either the 3590 or e10 set of sequences. Then, we evaluate the score between the target residue I and residue j of template jk as
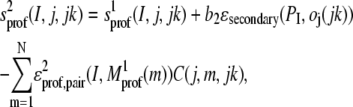 |
(3) |
where 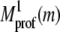 is the alignment of the mth template residue to the target sequence in template jk that was generated by the first pass using the sequence and secondary structure propensities of Eq. 2. C(j,m,jk) is the side-chain contact map of template jk. b2 = 0.4 (0.2) for the 3590 (e10) sequence profiles.
is the alignment of the mth template residue to the target sequence in template jk that was generated by the first pass using the sequence and secondary structure propensities of Eq. 2. C(j,m,jk) is the side-chain contact map of template jk. b2 = 0.4 (0.2) for the 3590 (e10) sequence profiles. 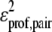 is the target's multiple sequence averaged, protein-specific pair potential (40).
is the target's multiple sequence averaged, protein-specific pair potential (40).
Alignments are generated using the local-global alignment extracted from dynamic programming (44,45). For the 3590 profiles, the gap opening and gap propagation penalties are −10.0 (−14.5) and −0.1 (−0.75) for the first (second) pass respectively. For the e10 profiles, the gap opening and gap propagation penalties are −7.0 (−14.0) and −05 (−1.05) for the first (second) pass, respectively. The final target-template score is evaluated as the difference between the score of the best alignment generated with the target sequence and the reverse order of the target sequence (46). This is designed to remove trivial composition dependent effects on scoring.
Second to fourth iteration with pair potentials and side-chain contact predictions
To generate contacts, for the top five scoring templates that have a Z-score >1.3 in each of the four scoring functions, the set of contacts is extracted. If a contact between residues I and I′ occurs in at least three of these templates, the total number of which is 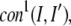 then it is counted as a predicted contact for the construction of the protein-specific pair potential used in the second iteration of Eq. 3 as follows,
then it is counted as a predicted contact for the construction of the protein-specific pair potential used in the second iteration of Eq. 3 as follows,
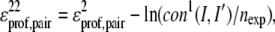 |
(4a) |
with nexp the expected number of contacts per residue if they are uniformly distributed, viz.
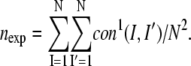 |
(4b) |
For the third and final iteration that includes the pair interaction contribution to the threading alignment, we repeat the above procedure but demand that a contact be present in at least four of the templates for the contact to be predicted.
Evolved and composite-sequence methods for contact prediction
The evolved-sequence method uses the identical formalism and parameters, but replaces the 3590 sequence profiles and MTX profiles in Eqs. 2–4 with the corresponding evolved sequence profiles. In practice, the alignments generated from the evolved-sequence method are more accurate than those using the wild-type template sequence profiles, but the coverage of the template is less. The average fraction of correctly predicted side-chain contacts over the benchmark set of proteins is 0.46, with the average fraction of predicted contacts per residue of 1.85. This compares favorably with the average fraction of correctly predicted contacts of 0.37 and coverage of 3.29 when the wild-type 3590 profiles are used. If we consider consensus contacts between the evolved sequence set and the original PROSPECTOR_3.5 predicted contacts, then the average fraction of accurately predicted contacts increases to 0.60, with the average number of contacts predicted per residue of 1.43. In what follows, we use the set of consensus-predicted contacts between PROSPECTOR_3.5 and the evolved-sequence version; we term this the composite-sequence method.
Structure assembly
The energy function in the original TASSER algorithm is composed of knowledge-based long- and short-range correlations, the propensity for predicted secondary structures extracted from PSIPRED (39), protein-specific pair interactions, and a residue-based solvent accessibility term (26,28,47). In TASSER_2.0, we introduce an additional contact restraint function to increase the effect of the new, and more accurate on average, contact restraints. For residues I and J predicted to be in contact using the composite-sequence method, their contact energy (Eadd) is defined by
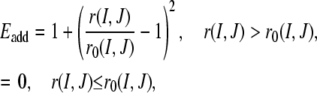 |
(5) |
where r(I,J) is the distance between the side-chain centers of mass of the Ith and Jth residues and r0(I,J) is the corresponding cutoff distance for a contact between their side-chain centers of mass.
TASSER_2.0 uses a protein representation composed of Cα atoms and the side-chain centers of mass. The aligned regions in the templates identified by PROSPECTOR_3.5 provide continuous fragments for assembly. For the unaligned regions provided by PROSPECTOR_3.5, we connect the continuous template fragments by random walk of Cα-Cα bond vectors to build an initial full-length model. From the initial full-length model, conformational space is searched by parallel hyperbolic Monte Carlo sampling (48), where 40 replicas are used, irrespective of target protein length.
Final model selection
After the structure assembly procedure is finished, the 14 lowest temperature replicas' trajectories are submitted to the structural clustering program, SPICKER (27). To assess the prediction, we compare the quality of the best among the top five TASSER_2.0 models with the best among the top five TASSER models as well as the best initial alignments from the PROSPECTOR_3.5 threading templates.
RESULTS AND DISCUSSION
Contact restraint prediction
According to the threading score significance and the consensus (if any) among the alignments of the top two templates, PROSPECTOR_3.5 categorizes target proteins as Easy, Medium, and Hard. This classification scheme indicates the relative confidence in the accuracy of prediction. From our previous work, the majority of Easy, Medium, and Hard sets have correct templates/alignments, correct templates with poor alignments, and incorrect templates/alignments, respectively (26). The Easy set has the highest predicted contact accuracy. Among the 2591 single domain benchmark proteins, PROSPECTOR_3.5 assigns 1802 proteins to the Easy set, 167 to the Medium set, and 622 to the Hard set (Data S1).
We calculate the fraction of accurately predicted contacts (Facc) by
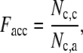 |
(6) |
where Nc,c is the number of common contacts in both the predicted contact restraints and the native structure, and Nc,a is the total number of the predicted contacts. In Table 1, we show the average fraction of accurate contacts, Facc, of the Easy, Medium, and Hard sets.  indicate the Facc from PROSPECTOR_3.5 and those from the composite-sequence method, respectively. Overall, the average
indicate the Facc from PROSPECTOR_3.5 and those from the composite-sequence method, respectively. Overall, the average 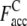 is 0.60, whereas the average
is 0.60, whereas the average 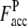 from PROSPECTOR_3.5 is 0.37. This shows that the composite-sequence method that takes consensus contacts generated by PROSPECTOR_3.5 using evolved and wild-type sequence profiles generates more accurate predicted contact restraints than those provided by the use of wild-type template sequence profiles alone. We note that a number of other methods, SVMcon (49), PROFcon (50), and Distill (51), reported an average accuracy of 0.3 in CASP7. For TASSER, this is too low to produce reasonably accurate models.
from PROSPECTOR_3.5 is 0.37. This shows that the composite-sequence method that takes consensus contacts generated by PROSPECTOR_3.5 using evolved and wild-type sequence profiles generates more accurate predicted contact restraints than those provided by the use of wild-type template sequence profiles alone. We note that a number of other methods, SVMcon (49), PROFcon (50), and Distill (51), reported an average accuracy of 0.3 in CASP7. For TASSER, this is too low to produce reasonably accurate models.
TABLE 1.
Fraction of accurately predicted contact restraints and predicted contacts per residue from the wild-type sequence and the composite-sequence methods
| Wild-type sequence method
|
Composite-sequence method
|
|||
|---|---|---|---|---|
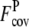 † †
|
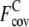 § §
|
|||
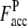 * [SD¶] * [SD¶] |
(contacts/residue) [SD] |
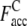 ‡ [SD] ‡ [SD] |
(contacts/residue) [SD] | |
| Easy set | 0.43 [0.15] | 3.75 [1.20] | 0.64 [0.19] | 1.87 [1.12] |
| Medium set | 0.30 [0.22] | 2.29 [0.93] | 0.51 [0.30] | 0.56 [0.51] |
| Hard set | 0.22 [0.17] | 2.25 [0.90] | 0.50 [0.34] | 0.25 [0.37] |
| All | 0.37 [0.18] | 3.29 [1.31] | 0.60 [0.25] | 1.43 [1.20] |
Average fraction of accurate predicted contacts using the wild-type template sequence profiles in PROSPECTOR_3.5.
Average fraction of predicted contacts per residue using the wild-type template sequence profiles in PROSPECTOR_3.5.
Average fraction of accurate predicted contacts from the composite-sequence method.
Average fraction of predicted contacts per residue from the composite-sequence method.
Standard deviation.
The Easy, Medium, and Hard sets have an average 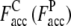 with ± SD (one standard deviation) of 0.64 ± 0.19 (0.43 ± 0.15), 0.51 ± 0.30 (0.30 ± 0.22), and 0.50 ± 0.34 (0.22 ± 0.17), respectively. Obviously, the accuracy of the predicted contact restraints of the composite-sequence method is significantly increased compared with those from use of the wild-type sequences alone in PROSPECTOR_3.5, irrespective of target difficulty. The statistical significance of the difference observed in the average fraction of accurate predicted contacts between the wild-type sequence method and composite-sequence method is also evaluated by a correlated two-tailed t-test (52) at a critical α-level set to a very restrictive 10−3. This t-test shows that for all levels of target difficulty, we can safely reject the null hypothesis that there is no significant change between composite-sequence method and wild sequence method (p-value of <10−300, 4.46 × 10−27, and 1.67 × 10−79 for the Easy, Medium, and Hard sets, respectively). Thus, we can safely conclude that the composite-sequence method increases the fraction of accurate predicted contacts. We especially note that the
with ± SD (one standard deviation) of 0.64 ± 0.19 (0.43 ± 0.15), 0.51 ± 0.30 (0.30 ± 0.22), and 0.50 ± 0.34 (0.22 ± 0.17), respectively. Obviously, the accuracy of the predicted contact restraints of the composite-sequence method is significantly increased compared with those from use of the wild-type sequences alone in PROSPECTOR_3.5, irrespective of target difficulty. The statistical significance of the difference observed in the average fraction of accurate predicted contacts between the wild-type sequence method and composite-sequence method is also evaluated by a correlated two-tailed t-test (52) at a critical α-level set to a very restrictive 10−3. This t-test shows that for all levels of target difficulty, we can safely reject the null hypothesis that there is no significant change between composite-sequence method and wild sequence method (p-value of <10−300, 4.46 × 10−27, and 1.67 × 10−79 for the Easy, Medium, and Hard sets, respectively). Thus, we can safely conclude that the composite-sequence method increases the fraction of accurate predicted contacts. We especially note that the 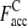 of 0.51 and 0.50 of the Medium and Hard sets is higher than
of 0.51 and 0.50 of the Medium and Hard sets is higher than 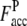 of 0.43 of the Easy set. We also calculate the fraction of predicted contacts per residue (Fcov = Nc,a/Nres, where Nres is the length of a target protein). As a trade-off for the significant improvement in contact accuracy, the average
of 0.43 of the Easy set. We also calculate the fraction of predicted contacts per residue (Fcov = Nc,a/Nres, where Nres is the length of a target protein). As a trade-off for the significant improvement in contact accuracy, the average 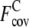 with ± SD of the composite-sequence method is reduced to 1.43 ± 1.20, compared with
with ± SD of the composite-sequence method is reduced to 1.43 ± 1.20, compared with 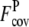 = 3.29 ± 1.31 when the wild-type 3590 template sequence profiles alone are used. For the Easy set, the average
= 3.29 ± 1.31 when the wild-type 3590 template sequence profiles alone are used. For the Easy set, the average 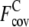 is 1.87 ± 1.12, whereas
is 1.87 ± 1.12, whereas 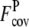 is 3.75 ± 1.20. For the Medium and Hard sets, the average
is 3.75 ± 1.20. For the Medium and Hard sets, the average 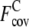 is also reduced to 0.56 ± 0.51 and 0.25 ± 0.37, compared with
is also reduced to 0.56 ± 0.51 and 0.25 ± 0.37, compared with 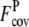 of 2.29 ± 0.93 and 2.25 ± 0.90, respectively. For all levels of target difficulty, the composite-sequence method provides more accurately predicted but fewer contacts per residue than the wild-type 3590 template sequence profiles.
of 2.29 ± 0.93 and 2.25 ± 0.90, respectively. For all levels of target difficulty, the composite-sequence method provides more accurately predicted but fewer contacts per residue than the wild-type 3590 template sequence profiles.
TASSER_2.0 refinement results
TASSER_2.0 uses the templates from PROSPECTOR_3.5 and predicted side-chain contact restraints from the composite-sequence method. In Table 2, we show the average root mean-square deviation (RMSD) to the native structure of the initial threading templates from PROSPECTOR_3.5 that uses the wild-type template sequence profiles, TASSER and TASSER_2.0 models. The mean target-template sequence identity is 19%, 16%, and 13% for Easy, Medium, and Hard sets, respectively. Overall, the average RMSD to the native structure of the TASSER models (± SD) is 4.73 ± 3.84 Å/5.31 ± 3.92 Å over the aligned regions/entire molecule, whereas the initial PROSPECTOR_3.5 templates have an average RMSD of 7.30 ± 5.44 Å over the aligned regions (the set of aligned residues in the PROSPECTOR_3.5 templates). The average RMSD of the TASSER_2.0 models is 4.42 ± 3.46 Å/4.99 ± 3.57 Å over the aligned regions/entire molecule, which is smaller than that of the TASSER models. This shows that the TASSER_2.0 models are closer to their native structures than either the TASSER models or the initial templates.
TABLE 2.
Comparison of models from TASSER_2.0, TASSER and PROSPECTOR_3.5
| 〈RMSD to the native〉, Å[SD*]
|
|||||||
|---|---|---|---|---|---|---|---|
| Num† | ID (%)‡ |
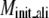 § §
|
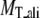 ¶ ¶
|
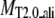 ‖ ‖
|
MT_all** | 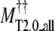 |
|
| Easy | 1802 | 19 | 5.60 [4.33] | 3.42 [2.55] | 3.27 [2.35] | 4.02 [2.80] | 3.86 [2.61] |
| Medium | 167 | 16 | 8.69 [5.16] | 5.39 [3.54] | 4.71 [2.77] | 5.82 [3.61] | 5.09 [2.87] |
| Hard | 622 | 13 | 11.87 [5.66] | 8.37 [4.57] | 7.69 [4.17] | 8.92 [4.48] | 8.24 [4.12] |
| All | 2591 | 17 | 7.30 [5.44] | 4.73 [3.84] | 4.42 [3.46] | 5.31 [3.92] | 4.99 [3.57] |
Standard deviation.
Number of target proteins in each category.
Average sequence identity of target-template sequences.
Average RMSD to the native structure of the initial PROSPECTOR_3.5 templates§, TASSER¶, and TASSER_2.0‖ models over the same aligned regions provided from PROSPECTOR_3.5.
Average RMSD to the native structure of TASSER** and TASSER_2.0†† models over the entire molecule.
As previously reported (26,28), for all levels of target difficulty, the average RMSD of the TASSER models is clearly smaller than that of initial templates from PROSPECTOR_3.5. For the Easy set, the TASSER_2.0 (TASSER) models have an average RMSD of 3.27 ± 2.35 Å/3.86 ± 2.61 Å (3.42 ± 2.55 Å/4.02 ± 2.80 Å) over the aligned region/entire molecule. For the Medium and Hard sets, the average RMSD of their TASSER_2.0 (TASSER) models is 4.71 ± 2.77 Å/5.09 ± 2.87 Å (5.39 ± 3.54 Å/5.82 ± 3.61 Å) and 7.69 ± 4.17 Å/8.24 ± 4.12 Å (8.37 ± 4.57 Å/8.92 ± 4.48 Å), respectively. To evaluate the statistical significance of the difference of the average RMSD between TASSER and TASSER_2.0, the correlated two-tailed t-test is also performed with a critical α-level set at a very restrictive 10−3. This t-test shows that there is a significant difference of average RMSD between TASSER and TASSER_2.0 models (p-value of 1.87 × 10−11, 3.10 × 10−4, and 1.40 × 10−15 for the Easy, Medium, and Hard sets, respectively) and we conclude that TASSER_2.0 improves the average RMSD compared with TASSER. We also calculate the TM-score that is also a measure of global protein structural similarity. The TM-score ranges from 0 to 1, with 0.30 the average value of the best structure alignment between a pair of randomly related protein structures independent of chain length (53), and when two structures are identical, their TM-score is 1.0. The average TM-score of the TASSER_2.0 (TASSER) models is 0.748 (0.743), 0.533 (0.516), and 0.460 (0.444) for the Easy, Medium, and Hard sets, respectively. These results show that irrespective of target difficulty: 1), the TASSER models become closer to the native structure than the initial templates and 2), TASSER_2.0, which incorporates more accurate predicted contact restraints than TASSER, also shows obvious improvement over TASSER as well as the initial template structures. The list of benchmark set proteins and results for all targets of TASSER and TASSER_2.0 models in the benchmark set may be found at http://cssb.biology.gatech.edu/skolnick/files/tasser2.0/.
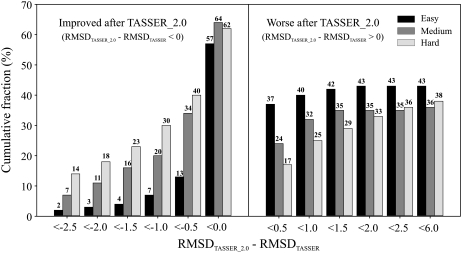
For a detailed comparison of the TASSER_2.0 and TASSER models, we show the histogram of the cumulative fraction of the RMSD difference between the TASSER_2.0 and TASSER models, ΔRMSD (RMSDTASSER_2.0 – RMSDTASSER) in Fig. 1. When the TASSER_2.0 model has a smaller RMSD than the TASSER model, ΔRMSD is negative. For the Easy set, 57% of the TASSER_2.0 models are closer to their native structures than the TASSER models. For the Medium and Hard sets, 64% and 62% of the TASSER_2.0 models have a smaller RMSD to native than the TASSER models. Among the improved cases, 22%, 53%, and 64% of the TASSER_2.0 models for the Easy, Medium, and Hard sets show an improvement in RMSD of more than 0.5 Å.
FIGURE 1.
Cumulative fraction of the RMSD difference between the TASSER_2.0 and TASSER models, RMSDTASSER_2.0 – RMSDTASSER, for the Easy, Medium, and Hard sets. When the TASSER_2.0 model has a smaller RMSD than the TASSER model, the difference is negative, indicating that TASSER_2.0 is better. When the difference is positive, TASSER_2.0 generates worse models because the RMSD of the TASSER model is smaller than the TASSER_2.0 model. The values of cumulative fraction (%) are shown in each histogram.
As already shown, using the wild-type template sequences in PROSPECTOR_3.5, the accuracy of the predicted contact restraints is quite dependent on the level of target difficulty, and for many cases, there is high contact coverage, but low accuracy. In this situation, the TASSER models that are generated with this large number (and fraction) of inaccurate contacts are highly frustrated and are far from their native structures. The composite-sequence method significantly increases the accuracy of contact restraints, irrespective of target difficulty. Even the Medium and Hard sets of the composite-sequence method have higher contact accuracy than that for the Easy set generated using wild-type sequence profiles, which has the most accurate contact restraints.
For the Easy set, their TASSER models are quite accurate because PROSPECTOR_3.5 provides a sufficient number of accurate contact restraints as well as correctly identified templates for the majority of cases. Thus, the opportunity for improvement by TASSER_2.0 is relatively small. On the other hand, for many Medium and Hard cases, the contact prediction accuracy in TASSER is quite low. By using the composite-sequence method to provide predicted contact restraints into TASSER_2.0, we significantly increase the contact accuracy and reduce the number of inaccurate contacts. Therefore, the conformational search is more efficient in finding structures that are closer to their native state.
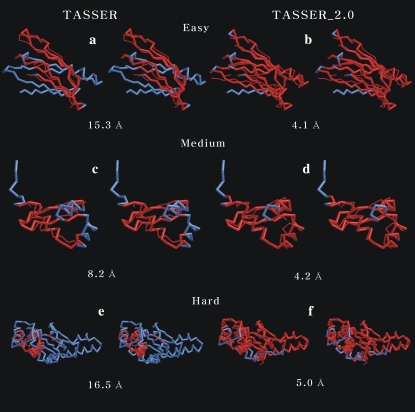
In Fig. 2, a–f, we show representative examples of the improvement of TASSER_2.0 over TASSER models. For the Easy set (Fig. 2, a and b; 1BM7A, 114 residues), the TASSER model has a RMSD to the native of 15.3 Å with 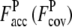 of 0.22 (1.50). The TASSER_2.0 model has a RMSD of 4.1 Å and
of 0.22 (1.50). The TASSER_2.0 model has a RMSD of 4.1 Å and 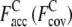 is 0.83 (0.69). For the Medium set (Fig. 2, c and d; 1XJHA, 62 residues), in TASSER_2.0, where
is 0.83 (0.69). For the Medium set (Fig. 2, c and d; 1XJHA, 62 residues), in TASSER_2.0, where 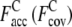 is 0.76 (0.34), the RMSD is smaller, 4.2 Å, as compared to the model generated by TASSER which has a RMSD of 8.2 Å due to the fact that
is 0.76 (0.34), the RMSD is smaller, 4.2 Å, as compared to the model generated by TASSER which has a RMSD of 8.2 Å due to the fact that 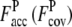 is 0.41 (1.16). For the Hard set (Fig. 2, e and f; 1KQ4A, 199 residues), the TASSER_2.0 model has a RMSD of 5.0 Å, compared with 16.5 Å for the TASSER model. The
is 0.41 (1.16). For the Hard set (Fig. 2, e and f; 1KQ4A, 199 residues), the TASSER_2.0 model has a RMSD of 5.0 Å, compared with 16.5 Å for the TASSER model. The 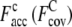 and
and 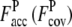 are 0.72 (0.87) and 0.40 (1.66), respectively, which shows the importance of improved accuracy at reasonable levels of structure coverage.
are 0.72 (0.87) and 0.40 (1.66), respectively, which shows the importance of improved accuracy at reasonable levels of structure coverage.
FIGURE 2.
Representative examples showing the improvement of the TASSER_2.0 models over the TASSER models for the Easy (1BM7A), Medium (1XJHA), and Hard (1KQ4A) sets. The thick (thin) line refers to the native structure (predicted model). The stereo images of TASSER and TASSER_2.0 models are on the left- and right-hand sides of the figure, respectively. Red indicates residue pairs having a distance <5 Å after the superposition of the predicted model onto the native structure. For the remainder of residues whose distance is ≥5 Å after superposition, the native structure is shown in blue (thick line). The RMSD to the native structure is shown below the models.
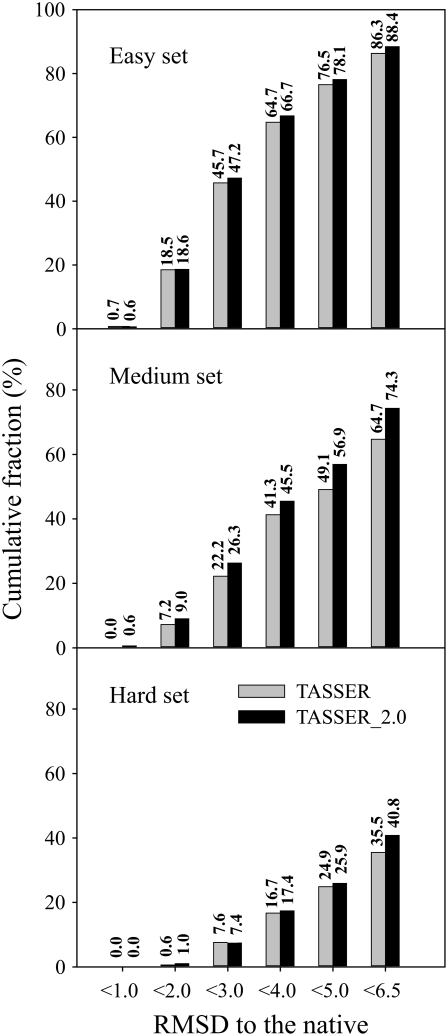
Fig. 3 shows a histogram of the RMSD distribution from TASSER and TASSER_2.0. To assess the results, we define a foldable protein as that when the RMSD to the native is <6.5 Å (26,28,36). TASSER_2.0 shows better performance than TASSER. For TASSER_2.0 (TASSER), the fraction of foldable proteins in the Medium set is 0.743 (0.647). This success rate decreases to 0.408 (0.355) for the Hard set. For the Easy set, TASSER_2.0 shows a success rate of 0.884, compared with 0.863 for TASSER. Overall, TASSER_2.0 has a higher fraction of foldable proteins of 0.761 as compared to 0.727 for TASSER.
FIGURE 3.
Cumulative fraction of proteins in the Easy, Medium, and Hard sets as a function of the RMSD to the native structure for the best of top five TASSER and TASSER_2.0 models.
In previous work, TASSERiter (36), which iteratively refines the original TASSER models, also showed improvement over TASSER. For the Easy, Medium, and Hard set proteins, their TASSER_2.0 (TASSERiter) models have an average RMSD to native of 3.86 Å (3.83 Å), 5.09 Å (4.90 Å), and 8.24 Å (8.44 Å) and a folding success rate of 0.884 (0.876), 0.743 (0.754), and 0.408(0.386), respectively. Comparing TASSER_2.0 with TASSERiter, the average RMSD of TASSER_2.0 is smaller than that of TASSERiter for the Hard set, whereas TASSER_2.0 has a slightly larger average RMSD for the Easy and Medium sets. For the Hard and Easy sets, TASSER_2.0 has a higher success rate than TASSERiter, whereas TASSER_2.0 has a marginally smaller success rate than TASSERiter for the Medium targets. These results show that TASSER_2.0 has comparable performance to TASSERiter (and is even better for the Hard set) but requires about a factor of 6 less simulation time.
We also calculate the fraction of proteins that are foldable (RMSDTASSER_2.0 < 6.5 Å) in TASSER_2.0 but not in TASSER (RMSDTASSER > 6.5 Å); 11% and 9% of the Medium and Hard proteins become foldable when TASSER_2.0 is used, whereas 3% of the Easy set targets show a corresponding improvement. Irrespective of target difficulty, TASSER_2.0 provides an increased fraction of foldable proteins, with the largest improvement seen for the Medium and Hard sets; the latter represents significant progress.
CONCLUSIONS
To improve the accuracy of TASSER, especially for difficult targets, we have developed the TASSER_2.0 algorithm that incorporates more accurate predicted side-chain restraints obtained from the composite-sequence contact prediction method. TASSER_2.0 was tested on a comprehensive, large-scale benchmark set consisting of 2591 nonhomologous single domain proteins (Data S1). TASSER_2.0 outperforms TASSER, especially for the Medium and Hard sets where the original contact prediction algorithm that uses wild-type template sequence profiles provides a large number of low accuracy contacts, whereas for many targets, the composite-sequence method provides contact predictions of acceptable accuracy and coverage. Therefore, TASSER_2.0 improves protein structure prediction quality especially for the more difficult targets; it also improves over the initial alignments from threading. Since the accuracy of TASSER_2.0 is strongly dependent on the accuracy of the predicted side-chain contacts, we plan in the near future to focus on the development of even more accurate tertiary restraint prediction approaches. What is encouraging is that the Medium targets are shifted to have the same quality as TASSER's more difficult Easy set targets, and the Hard targets, whose prediction quality was very poor in TASSER, show encouraging improvements. This suggests that for the most difficult targets, significant progress using template-based approaches to structure prediction can be made.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Acknowledgments
The authors thank Dr. Hongyi Zhou for developing the single sequence secondary structure prediction algorithm used for the evolution of template sequences, as well as for his very helpful comments and discussions about structural refinement, and Dr. Adrian K. Arakaki for help in preparation of the figures.
This research was supported in part by National Institutes of Health grant Nos. GM-48835 and GM-37408 and the Korea Research Foundation Grant funded by the Korean government (MOEHRD) (KRF-2005-214-C00146).
Editor: Ron Elber.
References
- 1.Murzin, A. G. 2001. Progress in protein structure prediction. Nat. Struct. Biol. 8:110–112. [DOI] [PubMed] [Google Scholar]
- 2.Pillardy, J., C. Czaplewski, A. Liwo, J. Lee, D. R. Ripoll, R. Kazmierkiewicz, S. Oldziej, W. J. Wedemeyer, K. D. Gibson, Y. A. Arnautova, J. Saunders, Y. J. Ye, and H. A. Scheraga. 2001. Recent improvements in prediction of protein structure by global optimization of a potential energy function. Proc. Natl. Acad. Sci. USA. 98:2329–2333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Moult, J., K. Fidelis, A. Kryshtafovych, B. Rost, T. Hubbard, and A. Tramontano. 2007. Critical assessment of methods of protein structure prediction-Round VII. Proteins. 69:3–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Skolnick, J. 2007. Protein Structure Prediction. The Encyclopedia of Life Sciences. In press.
- 5.Eswar, N., B. John, N. Mirkovic, A. Fiser, V. A. Ilyin, U. Pieper, A. C. Stuart, M. A. Marti-Renom, M. S. Madhusudhan, B. Yerkovich, and A. Sali. 2003. Tools for comparative protein structure modeling and analysis. Nucleic Acids Res. 13:3375–3380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rai, B., and A. Fiser. 2006. Multiple mapping method: a novel approach to the sequence-to-structure alignment problem in comparative protein structure modeling. Proteins. 63:644–661. [DOI] [PubMed] [Google Scholar]
- 7.Dunbrack, R. L. 2006. Sequence comparison and protein structure prediction. Curr. Opin. Struct. Biol. 16:374–384. [DOI] [PubMed] [Google Scholar]
- 8.Han, R., A. Leo-Macias, D. Zerbino, U. Bastolla, B. Contreras-Moreira, and A. R. Ortiz. 2007. An efficient conformational sampling method for homology modeling. Proteins. 71:175–188. [DOI] [PubMed] [Google Scholar]
- 9.Skolnick, J., and D. Kihara. 2001. Defrosting the frozen approximation: PROSPECTOR-a new approach to threading. Proteins. 42:319–332. [PubMed] [Google Scholar]
- 10.Zhou, H., and Y. Zhou. 2005. SPARKS 2 and SP3 servers in CASP6. Proteins. 61:152–156. [DOI] [PubMed] [Google Scholar]
- 11.Xu, J., F. Jiao, and L. Yu. 2007. Protein structure prediction using threading. Methods Mol. Biol. 413:91–122. [DOI] [PubMed] [Google Scholar]
- 12.Hardin, C., T. V. Pogorelov, and Z. Luthey-Schulten. 2002. Ab initio protein structure prediction. Curr. Opin. Struct. Biol. 12:176–181. [DOI] [PubMed] [Google Scholar]
- 13.Zhang, Y., A. Kolinski, and J. Skolnick. 2003. TOUCHSTONE II: a new approach to ab initio protein structure prediction. Biophys. J. 85:1145–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Jauch, R., H. C. Yeo, P. R. Kolatkar, and N. D. Clarke. 2007. Assessment of CASP7 structure predictions for template free targets. Proteins. 69:57–67. [DOI] [PubMed] [Google Scholar]
- 15.Zhou, H., and J. Skolnick. 2007. Ab initio protein structure prediction using chunk-TASSER. Biophys. J. 93:1510–1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sali, A., and T. L. Blundell. 1993. Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 234:779–815. [DOI] [PubMed] [Google Scholar]
- 17.Bowie, J. U., R. Luthy, and D. Eisenberg. 1991. A method to identify protein sequences that fold into a known three-dimensional structures. Science. 253:164–170. [DOI] [PubMed] [Google Scholar]
- 18.Bernstein, F. C., T. F. Koetzle, G. J. Williams, E. F. Meyer, Jr., M. D. Brice, J. R. Rodgers, O. Kennard, T. Shimanouchi, and M. Tasumi. 1977. The Protein Data Bank: a computer-based archival file for macromolecular structures. J. Mol. Biol. 112:535–542. [DOI] [PubMed] [Google Scholar]
- 19.Simons, K. T., C. Strauss, and D. Baker. 2001. Prospects for ab initio protein structural genomics. J. Mol. Biol. 306:1191–1199. [DOI] [PubMed] [Google Scholar]
- 20.Shan, Y., G. Wang, and H. X. Zhou. 2001. Fold recognition and accurate query-template alignment by a combination of PSI-BLAST and threading. Proteins. 42:23–37. [DOI] [PubMed] [Google Scholar]
- 21.Marti-Renom, M. A., A. Stuart, A. Fiser, R. Sanchez, F. Melo, and A. Sali. 2000. Comparative protein structure modeling of genes and genomes. Annu. Rev. Biophys. Biomol. Struct. 29:291–325. [DOI] [PubMed] [Google Scholar]
- 22.Yang, A. S., and B. Honig. 2000. An integrated approach to the analysis and modeling of protein sequences and structures. I. protein structural alignment and a quantitative measure for protein structural distance. J. Mol. Biol. 301:665–678. [DOI] [PubMed] [Google Scholar]
- 23.Kihara, D., and J. Skolnick. 2003. The PDB is a covering set of small protein structures. J. Mol. Biol. 334:793–802. [DOI] [PubMed] [Google Scholar]
- 24.Zhang, Y., I. Hubner, A. K. Arakaki, E. Shakhnovich, and J. Skolnick. 2006. On the origin and highly likely completeness of single-domain protein structures. Proc. Natl. Acad. Sci. USA. 103:2605–2610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang, Y., and J. Skolnick. 2005. The protein structure prediction problem could be solved using the current PDB library. Proc. Natl. Acad. Sci. USA. 102:1029–1034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhang, Y., and J. Skolnick. 2004. Automated structure prediction of weakly homologous proteins on a genomic scale. Proc. Natl. Acad. Sci. USA. 101:7594–7599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhang, Y., and J. Skolnick. 2004. SPICKER: a clustering approach to identify near-native protein folds. J. Comput. Chem. 25:865–871. [DOI] [PubMed] [Google Scholar]
- 28.Zhang, Y., and J. Skolnick. 2004. Tertiary structure prediction on a comprehensive benchmark on medium to large size proteins. Biophys. J. 87:2647–2655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhang, Y., A. K. Arakaki, and J. Skolnick. 2005. TASSER: an automated method for the prediction of protein tertiary structures in CASP6. Proteins. 61:91–98. [DOI] [PubMed] [Google Scholar]
- 30.Lee, S. Y., Y. Zhang, and J. Skolnick. 2006. TASSER-based refinement of NMR structures. Proteins. 63:451–456. [DOI] [PubMed] [Google Scholar]
- 31.Zhou, H., S. B. Pandit, S. Y. Lee, J. Borreguero, H. Chen, L. Wroblewska, and J. Skolnick. 2007. Analysis of TASSER-based CASP7 protein structure prediction results. Proteins. 69(Suppl. 8):90–97. [DOI] [PubMed] [Google Scholar]
- 32.Pandit, S. B., Y. Zhang, and J. Skolnick. 2006. TASSER-Lite: an automated tool for protein comparative modeling. Biophys. J. 91:4180–4190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhang, Y., M. DeVries, and J. Skolnick. 2006. Structure modeling of all identified G protein-coupled receptors in the human genome. PLos Comput. Biol. 2:88–99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Day, P. W., S. G. Rasmussen, C. Parnot, J. J. Fung, A. Masood, T. S. Kobilka, X. J. Yao, H. J. Choi, W. I. Weis, D. K. Rohrer, and B. K. Kobilka. 2007. A monoclonal antibody for G protein-coupled receptor crystallography. Nat. Methods. 4:927–929. [DOI] [PubMed] [Google Scholar]
- 35.Rosenbaum, D. M., V. Cherezov, M. A. Hanson, S. G. Rasmussen, F. S. Thian, T. S. Kobilka, H. J. Choi, X. J. Yao, W. I. Weis, R. C. Stevens, and B. K. Kobilka. 2007. GPCR engineering yields high-resolution structural insights into beta2-adrenergic receptor function. Science. 318:1266–1273. [DOI] [PubMed] [Google Scholar]
- 36.Lee, S. Y., and J. Skolnick. 2007. Development and benchmarking of TASSERiter for the iterative improvement of protein structure predictions. Proteins. 68:39–47. [DOI] [PubMed] [Google Scholar]
- 37.Skolnick, J., D. Kihara, and Y. Zhang. 2004. Development and large scale benchmark testing of the PROSPECTOR_3 threading algorithm. Proteins. 56:502–518. [DOI] [PubMed] [Google Scholar]
- 38.Skolnick, J., A. Kolinski, and A. R. Ortiz. 1997. MONSSTER: a method for folding globular proteins with a small number of distance restraints. J. Mol. Biol. 265:217–241. [DOI] [PubMed] [Google Scholar]
- 39.Jones, D. T. 1999. Protein secondary structure prediction based on position-specific scoring matrices. J. Mol. Biol. 292:195–202. [DOI] [PubMed] [Google Scholar]
- 40.Skolnick, J., A. Kolinski, and A. Ortiz. 2000. Derivation of protein-specific pair potentials based on weak sequence fragment similarity. Proteins. 38:3–16. [PubMed] [Google Scholar]
- 41.Edgar, R. C., and K. Sjolander. 2004. A comparison of scoring functions for protein sequence profile alignment. Bioinformatics. 20:1301–1308. [DOI] [PubMed] [Google Scholar]
- 42.Altschul, S. F., and E. V. Koonin. 1998. Iterated profile searches with PSI-BLAST-a tool for discovery in protein databases. Trends Biochem. Sci. 23:444–447. [DOI] [PubMed] [Google Scholar]
- 43.Zhou, H., and Y. Zhou. 2005. Fold recognition by combining sequence profiles derived from evolution and from depth-dependent structural alignment of fragments. Proteins. 58:321–328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Smith, T. F., and M. S. Waterman. 1981. Identification of common molecular subsequences. J. Mol. Biol. 147:195–197. [DOI] [PubMed] [Google Scholar]
- 45.Needleman, S. B., and C. D. Wunsch. 1970. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 48:443–453. [DOI] [PubMed] [Google Scholar]
- 46.Karplus, K., and B. Hu. 2001. Evaluation of protein multiple alignments by SAM-T99 using the BAliBASE multiple alignment test set. Bioinformatics. 17:713–720. [DOI] [PubMed] [Google Scholar]
- 47.Wu, S., J. Skolnick, and Y. Zhang. 2007. Ab initio modeling of small proteins by iterative TASSER simulations. BMC Biol. 5:17–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zhang, Y., D. Kihara, and J. Skolnick. 2002. Local energy landscape flattening: parallel hyperbolic Monte Carlo sampling of protein folding. Proteins. 48:192–201. [DOI] [PubMed] [Google Scholar]
- 49.Cheng, J., and P. Baldi. 2007. Improved residue contact prediction using support vector machines and a large feature set. BMC Bioinformatics. 8:113–121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Punta, M., and B. Rost. 2005. PROFcon: novel prediction of long-range contacts. Bioinformatics. 21:2960–2968. [DOI] [PubMed] [Google Scholar]
- 51.Bau, D., A. J. Martin, C. Mooney, A. Vullo, I. Walsh, and G. Pollastri. 2006. Distill: a suite of web servers for the prediction of one-, two- and three-dimensional structural features of proteins. BMC Bioinformatics. 7:402–409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Witt, P. L., and P. McGrain. 1985. Compared two sample means t tests. Phys. Ther. 65:1730–1733. [DOI] [PubMed] [Google Scholar]
- 53.Zhang, Y., and J. Skolnick. 2004. Scoring function for automated assessment of protein structure template quality. Proteins. 57:702–710. [DOI] [PubMed] [Google Scholar]