Abstract
Some theorists have argued that the immediate recency effect observed in free recall reflects the emptying out of the contents of a short-term memory buffer (Davelaar, Goshen-Gottstein, Ashkenazi, Haarmann, & Usher, 2005). Others have argued that immediate recency reflects the properties of temporal context used to cue free recall (Howard & Kahana, 2002). We examined immediate free recall of lists with an item from the middle of the list repeated at or near the end. If associative processes contribute to immediate recency, as predicted by the temporal context account, the neighbors of the initial presentation of the repeated item should show enhanced recall at the initial stages of immediate recall. Recall transitions early in output—and even the initiation of recall itself—showed evidence for temporally-defined associations that resemble those observed in recall from long-term memory. These results have strong implications for models of the immediate recency effect in free recall.
After more than thirty years of debate, no consensus exists as to the nature of the recency effect observed in the immediate recall of a list of words. Theorists in the 1960s and early 1970s (e.g. Atkinson & Shiffrin, 1968; Glanzer, 1972) argued that the recall of items presented just a few seconds ago was accomplished by emptying out the contents of a short-term buffer, or short-term store (STS). The discovery of the long-term recency effect observed in delayed recall when a distractor intervenes between each item in the list (Bjork & Whitten, 1974; Glenberg et al., 1980) raised questions about the scope of buffer models of recency. After a period of debate about the empirical status of the long-term recency effect (e.g. Healy & Parker, 2001; Thapar & Greene, 1993; Watkins, Neath, & Sechler, 1989) a consensus emerged that the long-term recency effect cannot be accounted for by classical notions of STS. This is not to say, however, that the existence of the long-term recency effect contradicts the STS account of immediate recency—Atkinson and Shiffrin (1968) certainly never claimed that displacement from STS was the only cause of forgetting (Raaijmakers, 1993). However, the existence of the long-term recency effect raised the possibility that the immediate and long-term recency effects share a common mechanism (Greene, 1986).
Models that have attempted to provide a common explanation for both immediate and long-term recency have fallen into two classes. Models based on distinctiveness argue that the memories exist on a temporal dimension (Brown, Neath, & Chater, unpublished manuscript; Murdock, 1960; Nairne, Neath, Serra, & Byun, 1997; Neath & Brown, 2006; Neath & Crowder, 1990). Long-term recency in this framework is explained as something analogous to a Weber-Fechner law for memory retrieval, in which the end-of-list items stand out from their neighbors if they were presented even further in the past. Contextual variability models have also been proposed to account for the long-term recency effect. The starting point for these models is that explicit retrieval of items from memory relies on a mental representation that is part of the participants’ experience in learning the list but separate from the items on the list per se. Anderson and Bower (1972), drawing on Estes (1955), postulated that the encoding context of adjacent lists should be more similar to each other than lists that are separated by a longer duration (see also Mensink & Raaijmakers, 1988; Yntema & Trask, 1963). This idea of variable encoding context resonated with some early theorists considering the long-term recency effect (Glenberg et al., 1980); perhaps a gradually-changing encoding environment could account for the long-term recency effect within temporally-extended lists as well.
The major limitation of both contextual variability and distinctiveness accounts of the long-term recency effect is that they cannot readily explain the temporally-defined associations that form between words presented in a series. Kahana (1996) introduced the lag-CRP to measure the probability of free recall transitions as a function of the difference in the encoding serial positions, or lag, between the two items. These temporally-defined associations have been shown to exhibit a contiguity effect; items presented close together in the list tend to be associated. They also exhibit an asymmetry such that forward recall transitions are more likely than backward recall transitions. These properties have been observed across all the major episodic recall paradigms (see Kahana, Howard, & Polyn, in press, for a review).
Whereas variable context models do not have a natural means to predict temporally-defined associations, buffer models naturally predict them if the strength of the connection in long-term memory between items that are active together in the buffer is incremented as in the search of associative memory (SAM) implementation of the buffer model (SAM, Raaijmakers & Shiffrin, 1980). This buffer account of temporally-defined associations suffers from the same potential weakness as does the buffer account of recency effects—temporally-defined associations are also observed in continual-distractor free recall, in which a delay filled with a demanding distractor intervenes between all the items in the list (Howard & Kahana, 1999). If STS is not readily able to explain the long-term recency effect because of the end-of-list distractor, how is it possible that items could be maintained across the inter-item distractor interval to allow associations to form between those items?
Howard and Kahana (1999) proposed a retrieved context model in which a variable context signal is recovered by the recalled items. According to this view, when an item is recalled, it retrieves the state of the contextual signal that obtained when the item was originally presented. This retrieved contextual signal is used as a cue for recall of other items. This retrieved context overlaps to some extent with the encoding context of nearby items in a way analogous to the way test context overlaps with the encoding context of items from the end of the list in generating the long-term recency effect. According to this view, the temporally-defined associations observed in continual-distractor free recall are analogous to a long-term recency effect in which recency is measured relative to the just-recalled item. Howard and Kahana refined and formalized this idea in the temporal context model (TCM, Howard, Fotedar, Datey, & Hasselmo, 2005; Howard & Kahana, 2002; Howard, Kahana, & Wingfield, 2006).
One of the problems that needs to be solved in implementing a retrieved context model is the decision about when to recover context and when to evolve context randomly. TCM solves this problem by assuming that retrieval always takes place, even during study. Context evolves as a consequence of list items recovering pre-experimental contextual information. In a randomly-assembled list of words, these uncorrelated contexts mimic the random variation in a variable context model. However, when an item is repeated, retrieval of context induces a correlation between the recovered context and the state of context that obtained when the item was initially studied, leading to contiguity effects. That is, according to TCM, temporal context changes gradually from moment to moment during both study and test as a consequence of the retrieval of prior states of context by items, both studied and recalled. In TCM, repetition of an item can trigger recall of contextual features that were present during prior encounters with that item. Because these features are part of the encoding context of the repeated items’ neighbors, this facilitates recall of items that were previously studied close in time to the repeated item—a contiguity effect. This logic should hold regardless of whether the repetition is the consequence of recalling an item or as a consequence of a repeated study presentation in the list. Moreover, this contiguity effect should be observed not only during the later stages of delayed recall but even during the early stages of immediate recall.
Recently, Davelaar et al. (2005) argued that the framework provided by TCM is insuffcient to describe dissociations between immediate recency and the long-term recency effect (see also Talmi, Grady, Goshen-Gottstein, & Moscovitch, 2005). In order to explain these dissociations while also explaining the persistence of recency and contiguity effects across a delay, Davelaar et al. (2005) proposed a hybrid model in which a sophisticated variant of a buffer model of STS was combined with a variable context model of long-term store (LTS). As in classic buffer models, Davelaar et al. (2005) attribute the heightened lag-CRP in the early stages of immediate recall to the initial dumping of active items from the short-term memory buffer responsible for the immediate recency effect. Because the items present in the buffer at the time of test will tend to be from the end of the list, successively recalled items early in output will tend to be from nearby serial positions, leading to a contiguity effect. Notably, like previous buffer models, this account argues that the lag-CRP at early stages of immediate free recall is not a consequence of associative processes between successive recalls. That is, according to buffer models of immediate recency, recall of one item from short-term store does not cause recall of the next. Rather the contiguity effect is due to the property that items from nearby serial positions—in particular the end of the list—happen to occupy the buffer.
Although buffer models and TCM share the prediction that there should be contiguity effects in the early stages of immediate free recall, they are differentiated by their prediction about whether the mechanism giving rise to these contiguity effects is genuinely associative or not. Buffer models, including both the hybrid model (Davelaar et al., 2005) and SAM (Raaijmakers & Shiffrin, 1980), predict that the contiguity effect observed in the lag-CRP in the early stages of free recall should be non-associative. In contrast, TCM predicts that even in the early stages of immediate free recall, recall of an item can recover contextual information that contributes to the observed contiguity effects. According to TCM, there is a causal relationship between recall of one item and recall of the next, even in immediate recency. In order to differentiate these accounts of immediate recency, we examined the effect of repeating an item from the middle of the list near the end of a list on immediate recency.
Experiment
To assess whether temporally-defined associative processes play a role in immediate recency we examined immediate free recall of lists in which an item from the middle of the list was repeated at or near the end of the list. Recall of these experimental lists was compared with control lists that did not include a repeated item.
If TCM’s account of serial position effects applies to immediate free recall, then repetition of an item from the middle of the list should result in a recall advantage for neighbors of that item relative to control lists during the first several output positions of the immediate recency effect. When the repeated item is recalled at early output positions, it should recover contextual information from the original presentation of the item. This, in turn will result in a boost in the probability of recall for neighbors of the original presentation of the repeated item. For instance, if the repeated item was presented at serial position 5 and at the end of the list, then recall of the repeated item should be followed by enhanced recall of items from positions 4 and 6 over more remote neighbors of the repeated item (e.g. 3 or 7).
Further, TCM predicts that a similar advantage for the neighbors of the repeated item should be observed in recall initiation. That is, if the fifth item is repeated in the last serial position, then the repetition should recover contextual information similar to that observed when the item was initially presented. This information should be part of the contextual cue that is used to initiate immediate free recall. Because the overlap between this contextual signal and the encoding contexts of the items determines the cue strengths on the first recall attempt, this should result in a boost in the probability of initiating immediate free recall with the fourth or sixth item.
Method
Subjects performed immediate recall of 48 ten-item lists presented under conditions designed to discourage rehearsal. Half of the lists were experimental lists with a repeated item from one of four conditions; each experimental condition contributed 6 lists. In the 5,9 condition, the item presented in serial position 5 was repeated at serial position 9. In the 5,10 condition, the item presented in serial position 5 was repeated in serial position 10. Conditions 6,9 and 6,10 repeated the item from serial position 6 in serial position 9 and serial position 10 respectively. The other half of the lists were control lists, without any repeated items. Control lists were included to provide a baseline for performance attributable to the recency effect.1 We will attribute the discrepancy between experimental and control conditions to associative processes mediated by the repeated item. The items composing each list and the order of conditions was randomized separately for each subject.
The selection of experimental conditions was done to minimize strategic factors that might result in different amounts of attention at various serial positions in anticipation of a repeated item. The use of both 5,X and 6,X conditions (as well as the fact that half the lists did not include a repeated item) prevented the participants from anticipating that the item at one particular serial position would be repeated. The use of both X,9 and X,10 conditions made it such that participants would not take the presence of a repeated item as a proxy for a recall initiation cue. Further, the fact that half of the lists contained no repetitions at all would presumably mitigate strategic processing surrounding repeated items.
Participants
Two-hundred-ninety-four participants participated for course credit in an introductory psychology class at Syracuse University.
Materials
Study lists consisted words chosen without replacement from the noun subset of the Toronto word pool (Friendly, Franklin, Hoffman, & Rubin, 1982). Lists were chosen separately for each subject. Control lists consisted of ten distinct items. Experimental lists consisted of nine unique words, one of which was repeated appropriate to the condition as described above.
Procedure
Each study word was presented both auditorally and visually. For each study word, participants were required to press one of the control keys to indicate whether the word was concrete or abstract. If participants did not respond within 1200 ms the computer would buzz and advance to the next word in the list. When participants responded within 1200 ms, their answer was recorded and the next word followed after a delay of 500 ms.
After the last item was erased from the screen (typically following a response to the orienting task), the screen remained blank for 500 ms. Following this, a row of asterisks was displayed for 400 ms. Simultaneously an auditory signal was played over the speaker indicating that participants were to recall as many items from the list in any order. Participants were then given 30 s for verbal free recall. Vocal responses were recorded for later scoring with an off-line semi-automated parsing algorithm. At the very end of the session, participants were given five minutes for a surprise final free recall test. The results of the final free recall session are discussed elsewhere (Howard, Youker, & Venkatadass, submitted).
Results and Discussion
Orienting task
The vast majority of participants performed very well on the orienting task. Three participants who responded to less than.8 of the study words were excluded from further analysis. The remainder of the participants responded to .949 ± .002 (M ± SE) of the items. The mean response time, averaged across participants, to the orienting probes was 812 ± 4 ms. The average standard deviation of the response time was 139 ± 1 ms. To assess the quality of participants’ responses to the orienting task, we calculated the correlation between participants’ concrete/abstract judgments and ratings of concreteness reported by Friendly et al. (1982). The average correlation was.569 ± .007, with a range from.13 to.76. Even the lowest of these correlations was significantly different from zero at the.001 level. We conclude that participants attended to the orienting task, suggesting that resources available for rehearsal would be minimized.
Traditional serial position analyses
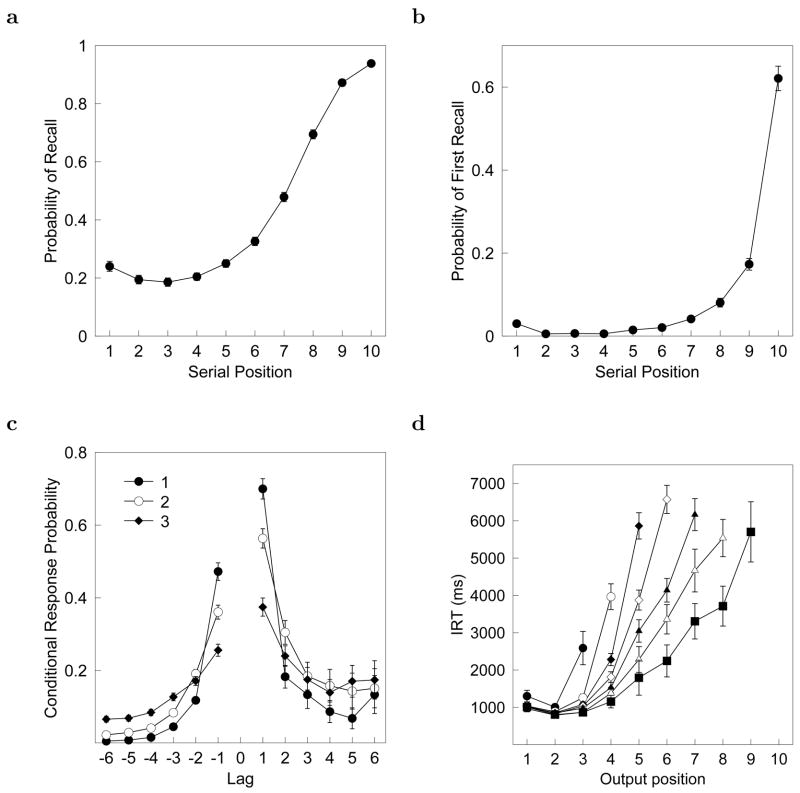
We conducted a series of analyses on the control data to illustrate benchmark findings from immediate free recall. Figure 1a shows the serial position curve (probability of recall as a function of serial position) for the control data. Although the serial position curve shows a pronounced recency effect typical of immediate free recall experiments, the primacy effect is much more modest than one would expect from studies in which no effort was made to disrupt rehearsal (e.g. Murdock, 1962). The lack of a primacy effect in the serial position curve suggests that the orienting task and rapid self-paced presentation time were successful in disrupting rehearsal.
Figure 1.
The recency effect in the control condition. a. Serial position curve. b. Probability of first recall (PFR) curve. c. The conditional response probability as a function of lag (lag-CRP) for the first three output positions. d. Growth of inter-response time (IRT) curves. Different curves correspond to trials in which different numbers of items were recalled. Error bars are 95% confidence intervals on all panels. Note: a and b also appear in Figure 1 of Howard, Youker, and Venkatadass (submitted).
Serial position curves for all experimental conditions are shown in Table 1. Although there is some evidence for associative effects in the probability of recall for the neighbors of the repeated item, these findings could reflect recall from long-term memory rather than immediate recency.
Table 1.
Probability of recall for each serial position and each condition. Numbers in parentheses are 95% confidence intervals.
| Serial Position | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cond | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Cont | .24(.02) | .19(.01) | .18(.01) | .20(.01) | .25(.01) | .33(.01) | .48(.02) | .69(.02) | .87(.01) | .94(.01) | |
| 5,9 | .23(.02) | .21(.02) | .19(.02) | .21(.02) | .92(.01) | .38(.03) | .53(.03) | .68(.02) | — | .94(.01) | |
| 5,10 | .24(.02) | .19(.02) | .18(.02) | .20(.02) | .94(.01) | .36(.03) | .53(.03) | .71(.02) | .85(.02) | — | |
| 6,9 | .23(.02) | .17(.02) | .21(.02) | .21(.02) | .28(.02) | .93(.01) | .58(.02) | .71(.02) | — | .94(.01) | |
| 5,10 | .22(.02) | .18(.02) | .18(.02) | .20(.02) | .27(.02) | .95(.01) | .54(.03) | .74(.02) | .88(.02) | — | |
Previous work has characterized the initiation of recall in immediate recency using the probability of first recall (PFR), a serial position curve calculated for the very first recall participants make. Figure 1b shows the PFR curve calculated for the control condition. As can be seen from the Figure, the dominant feature is a monotonically decaying recency effect. While this finding is consistent with other free recall experiments with verbal responses and orienting tasks designed to minimize rehearsal (Howard & Kahana, 1999; Kahana, Howard, Zaromb, & Wingfield, 2002), other immediate free recall experiments have observed a “plateau” at the end of the list (see the re-analysis of Murdock, 1962 and Murdock & Okada, 1970 in Laming, 1999). The plateau is more consistent with what one might expect from retrieval from a fixed capacity STS with a random item selection rule to initiate recall.
Figure 1c shows the lag-CRP separated for successive output positions. The curve labeled “1” in Figure 1c describes the transition from the first word recalled to the second word recalled. Similarly, the curve labeled “2” shows the lag-CRP for the transition between the word recalled second and the word recalled third. Consistent with prior findings (Howard & Kahana, 1999; Kahana, 1996), Figure 1c shows that the lag-CRP gradually decreases in magnitude as recall progresses over the first several output positions. The lag-CRP observed at output position 3 is similar to the contiguity effects observed at later output positions in immediate free recall and in delayed recall (Howard & Kahana, 1999; Kahana, 1996; Kahana et al., 2002) in other studies.
Figure 1d shows the growth in inter-response times (IRTs) as a function of output position calculated for the control conditions. The IRT is the delay between the time of onset of recall of one word and the onset of its successor. For the purpose of this analysis, we defined the IRT for the first recall as the amount of time from the onset of the recall cue to the initiation of verbal recall of the first item. The curves are separated according to how many words the participant recalled on any particular trial. The analysis in Figure 1d did not treat intrusions or repeated recalls differently from correct recalls. Consistent with prior work (Murdock & Okada, 1970), the first several recalls are quite fast, followed by a rapid rise in the recall of subsequent items, consistent with a transition from fast retrieval from STS to slower retrieval from LTS (Raaijmakers & Shiffrin, 1980). If this interpretation is correct, Figure 1d suggests that the first three or so recalls are from the buffer on the vast majority of trials on the control lists.
In sum, Figure 1 illustrates that the data from the control condition shows all the hallmarks of immediate recency observed in previous work. It is possible that although immediate recall of the control lists uses retrieval from STS, the inclusion of a repeated item somehow causes subjects to rely on long-term memory in the early stages of immediate free recall.
Associations in early recall transitions
We conducted a series of analyses on the recall transitions in the early stages of immediate recency to determine if associative effects contribute to these transitions and, if so, to determine whether the properties of these temporally-defined associations correspond to those observed in recall from long-term memory (Kahana, 1996; Kahana et al., in press, see also Figure 1c, output position 3). For these analyses, we observed the first two recall transitions—the transition from the first-recalled word to the word recalled second and the transition from the second-recalled word to the word recalled third. If temporally-defined associations contribute to these recalls, then we would expect to see an excess of recalls to the neighbors of the first presentation of the repeated item in the experimental conditions. For example, in condition 5,10, we would expect to see an excess of transitions to serial position 6 and serial position 4 above what we would expect from a purely recency-based account.
For each of the experimental conditions, we restricted our attention to instances in which the repeated item was the first word in a recall transition and the second item was a correct recall. For each experimental condition, we calculated a separate control measure from the data from the control condition. In this control analysis, we used exactly the same analysis as we used for the corresponding control condition, but relative to transitions from the serial position in the control list corresponding to the serial position of the second repetition of the item in the experimental condition.2 For instance, in calculating the control measure for the 5,9 condition, we would calculate the probability of recall following recall of the ninth item from the control list in the first two output positions.
To allow direct comparison with the experimental condition we also excluded transitions in which the second member of the pair was presented in the serial position of the first presentation of the repeated item. For example, in calculating the control measure for the 5,9 condition, we did not include transitions from the ninth item to the fifth item.
The control measure for each experimental condition estimates the probability of a transition to each serial position that would be expected as a consequence of recency, and also any associative processes relative to the serial position of the second presentation of the repeated item. Any discrepancy between the experimental and control measures around the serial position of the first presentation of the repeated item should be due to temporally-defined associations between the repeated item and the neighbors from its initial presentation.
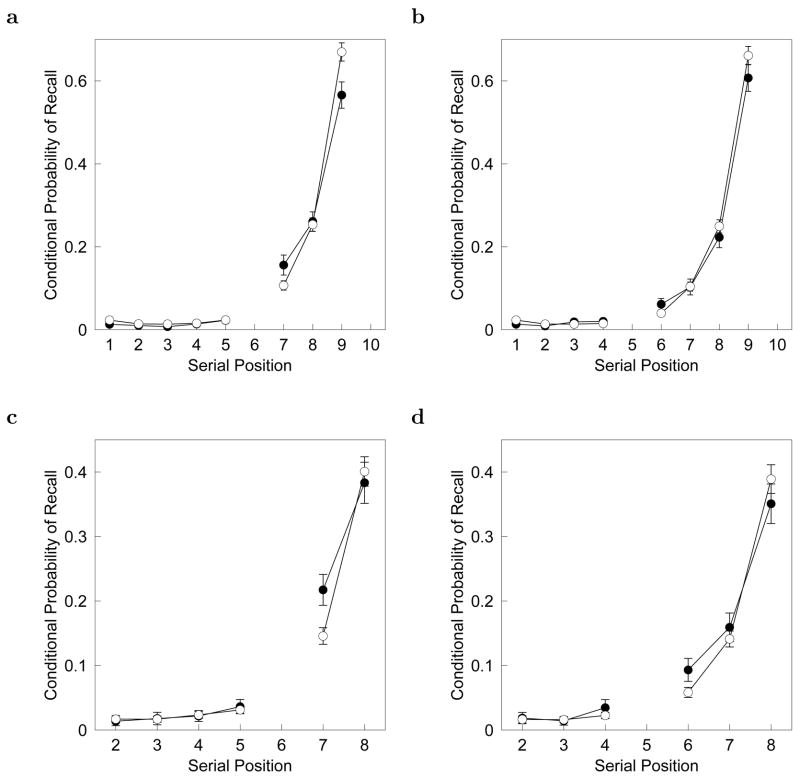
Figure 2 shows the results of this analysis for each of the four experimental conditions and the corresponding analysis of the control condition data. The most prominent feature of these data is the pronounced recency effect that extends several serial positions. In addition to the recency effect, however, there also appears to be an increase in the probability of a recall transition from the repeated item to the neighbors of the initial presentation of the repeated item. For instance, in Figure 2a, which displays data from the 6,10 condition, there appears to be an increase in the probability of recall transitions to serial position 7 over what was observed in the control data. Examining the curves in Figure 2, one is readily convinced that there is an associative advantage for serial positions that followed the initial presentation of the repeated items. There are also hints that an effect is observed for the items that preceded the initial presentation of the repeated item. In order to quantify these impressions, as well as examine the nature of these associations in isolation from the recency effect, we undertook subsequent analyses.
Figure 2.
Probability of a recall transition in the first two output positions from the repeated item to each serial position. Each panel shows data from one experimental condition (filled circles) with the corresponding analysis of the data from the control condition (open circles). a. Condition 6,10. b. Condition 5,10. c. Condition 6,9. d. Condition 5,9. Note the change in axes for conditions 6,9 and 5,9 compared to conditions 6,10 and 5,10. Error bars in all panels are 95% confidence intervals.
The goals of this lag analysis were to collapse the data observed in Figure 2 across conditions and examine the effect of lag to the initial presentation of the repeated item. For instance, if we are examining condition 5,10, the lag to serial position 6 is defined as +1 because item 6 immediately followed the initial presentation of the repeated item, which came at serial position 5. Similarly, the lag to serial position 3 would be −2 because item 3 preceded the initial presentation of the repeated item in condition 5,10 by two serial positions.
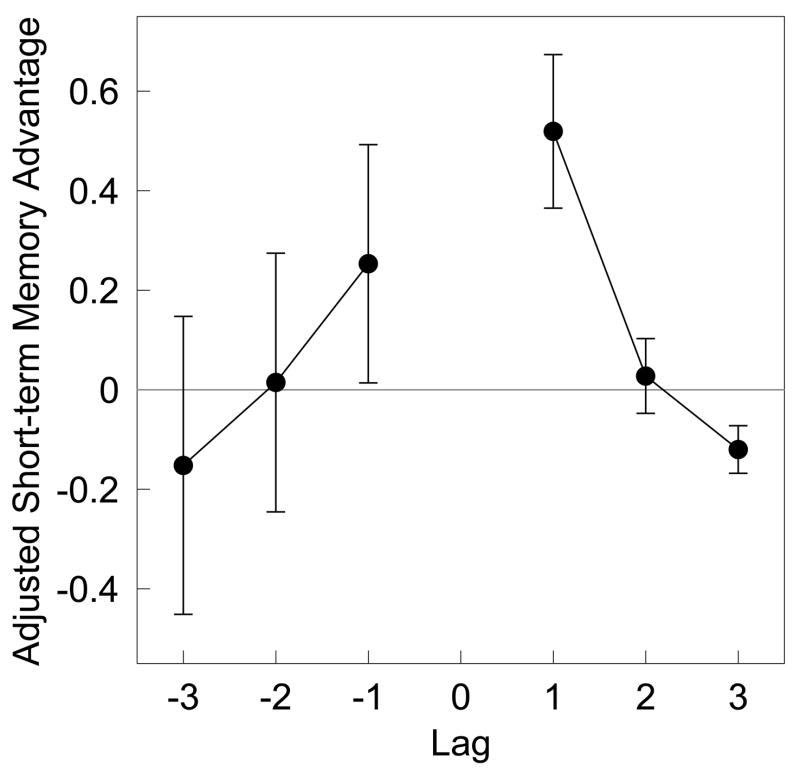
Lags from different conditions correspond to different serial positions. We took several steps to control for the recency effect in collapsing the data in Figure 2 across conditions. We first calculated the difference between each participant’s experimental measure and his or her control measure at each serial position for each condition. We then divided the difference score from each condition by the mean of the control data in that serial position before averaging each lag across conditions. The result is a number that describes the change in the probability of a recall transition from the repeated item to the neighbors of its initial presentation attributable to associative processes expressed. This value is the magnitude of the associative effect expressed as a proportion of the value expected from the control data. For instance, a value of.1 for a particular lag would mean that across conditions, recall transitions from the repeated item to the item in the appropriate serial position were 10% more likely than the value at that serial position estimated from the control data. The control data includes the effect of recency and any associative influence attributable to the item in the serial position corresponding to the repeated item in the corresponding experimental list. Finally, we note that the nature of this measure is such that a positive value at one lag results in a negative value at another lag. Because only one item can be recalled at any transition, if a transition to one item becomes more likely, transitions to other items are necessarily less likely.
Figure 3 shows the results of this lag analysis. The similarity of the shape of the curve in Figure 3 and the shape of lag-CRP curves observed in standard free recall from long-term memory (e.g. Kahana, 1996; Kahana et al., 2002, see also later output positions in Figure 1c) is striking. The hallmarks of transitions in episodic recall are a contiguity effect, shown here as a peak around zero and an asymmetry, shown as an increase in recall transitions to lags in the forward direction (e.g. +1) over transitions in the backward direction (e.g. −1). These properties have been illustrated extensively in a number of studies from all of the major episodic recall paradigms (see Kahana et al., in press, for a review). To determine if the apparent effect of lag is reliable, we calculated a linear regression in each recall direction for each participant. The average slope of the regression in the forward direction, −0.32 ± .04 was highly significant, t(289) = 7.25, p <.001, indicating a strong effect of lag on recall transitions in the forward direction. The average slope of the regression to lag in the backward direction, 0.20 ±.09, was also significantly different from zero, t(289) = 2.15, p <.05, indicating that there was also an effect of lag on recall transitions in the backward direction taken in isolation. The fact that there was an effect of lag for both forward and backward recall transitions, and that these effects went in opposite directions, rule out a confound with recency—such a confound would be expected to result in a lag effect in one direction or the other, but not both.
Figure 3.
Associations in the first two output positions of immediate recall after controlling for the effect of recency. See text for details. Error bars are 95% confidence intervals.
The lag analysis reveals that although the advantage for neighbors of the initial presentation of the repeated item may be small in absolute terms (Figure 2), the relative magnitude of the effect is considerable—words that immediately followed the initial presentation of the repeated item are about 50% more likely to be recalled following recall of the repeated item than one would expect from the control data. The apparent decrease at more remote lags is a consequence of the zero-sum nature of this measure—if the probability of recalling one item on a particular recall attempt is enhanced, the probability of recalling other items is necessarily decreased.
Associative processes in recall initiation
The foregoing analyses were able to isolate a temporally-defined associative effect in the early stages of immediate recall that was not attributable to recency per se. A parsimonious explanation of these findings is that associative mechanisms that give rise to temporally-defined associations are present even in immediate recency, in contrast with the predictions of extant models of STS (Atkinson & Shiffrin, 1968; Davelaar et al., 2005; Kahana, 1996).
The claim that the first two recall transitions ought to be from the short-term buffer, if that account is correct, seems reasonable on its face (Figure 1). One could argue, however, that even these very early recall transitions from one of the last two items in the list are contaminated by long-term memory processes. To control for this possibility, we examined the effects of repetition on the initiation of recall. That is, if the cue for immediate recency is temporal context, along the lines proposed by Howard and Kahana (2002), then there should be some advantage for the neighbors of the repeated item in starting recall, even though no items have yet been recalled.
Before describing these analyses and their results, we describe the tendency to recall the repeated item first. This effect is perhaps interesting in its own right and is important for motivating some aspects of the associative analyses that are presented later.
Table 2 shows the probability of first recall for the repeated item in the various experimental conditions in the column labeled “Repeated.” The column labeled “Control sum” gives the PFR that would be expected from summing the PFR from the corresponding serial positions in the control condition. For instance, the control sum for condition 5,9 is the sum of the PFRs for serial positions 5 and 9 from the control condition. In all four experimental conditions the PFR for the repeated item was significantly larger than would be expected by adding the corresponding serial positions from the control condition. This finding is not predicted by traditional buffer models of STS without elaboration. If the probability of an item entering the buffer is higher if a copy of that item is already present in STS, this result might make sense. However, Atkinson and Shiffrin (1968) used precisely the opposite assumption in describing effects in continuous paired associate learning.
Table 2.
The probability of recalling the repeated item in each first experimental condition at the first output position and the sum of the probability of first recall for the corresponding serial positions from the control condition.
| Condition | Repeated | Control sum | t(289) |
|---|---|---|---|
| 6,10 | .78 | .65 | 11.10 |
| 5,10 | .77 | .64 | 11.06 |
| 6,9 | .28 | .19 | 6.61 |
| 5,9 | .26 | .19 | 6.56 |
Our goal is to assess any boost in the PFR for the neighbors of the initial presentation of the repeated item. We will restrict our attention to conditions X,10 because the effect of the repeated item on recall initiation should presumably be greater if the repetition immediately precedes recall.3 Moreover, because our interest was in properties of the recency effect, we tried to eliminate participants who might have been engaging in serial recall on some percentage of trials from the analyses. We excluded all participants who had a PFR of greater than 0.1 for the first serial position. This left 276 participants for the subsequent analyses.4
In order to compare the PFR from the experimental conditions to the control data, we first need to compensate for the super-additivity of the effect of repetition on recall initiation; because the PFR is constrained to sum to 1.0, a super-additive increase in the PFR for the repeated item will pull down the PFR for the other items in the experimental condition relative to the corresponding items in the control condition. To this end, we renormalized the experimental PFRs so that the sum of the renormalized PFRs for the non-repeated items summed to 1 for each participant. This was not possible in cases where the participant always recalled the repeated item first in one of the experimental conditions. Because the participants only received 6 trials in each of the experimental conditions, this excluded a relatively large number of participants from the subsequent analyses. A total of one-hundred-forty-nine participants recalled the repeated item first on every trial for either condition 5,10 or 6,10. After renormalizing the PFRs from the experimental conditions, we calculated a renormalized version of the control PFR for each of the experimental conditions. For instance, in calculating the control for condition 5,10 we renormalized the control PFR omitting serial position 5 and 10 so that each participants’ renormalized PFR summed to 1.0; five participants recalled the last item first on every control trial, making renormalization impossible.
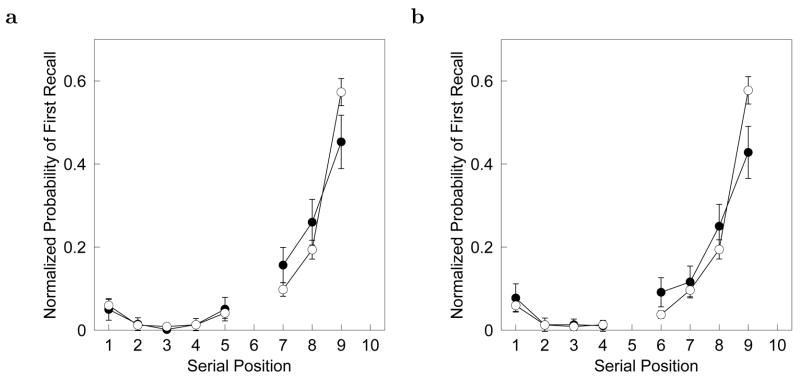
Figure 4 shows the renormalized PFR and the corresponding renormalized control PFR for the two experimental conditions in which the repeated item appeared in the last serial position. Again, the most obvious feature of these data is the pronounced recency effect that extends over essentially the entire list. In addition to the recency effect, there also appears to be an advantage for the neighbors of the repeated item over the control PFRs in the forward direction. For instance, in panel a of Figure 4, there appears to be an advantage for serial position 7 in the experimental data relative to the control analysis.
Figure 4.
Renormalized probability of first recall curves and corresponding control measures from the X,10 conditions. Data from experimental conditions is shown with filled circles. The corresponding control PFRs are shown with open circles. a. Condition 6,10. b. Condition 5,10. Error bars reflect 95% confidence intervals.
To systematically compare the effect of lag on the renormalized PFR across conditions we conducted a lag analysis. The relationship between this analysis and the renormalized PFR shown in Figure 4 is precisely analogous to the relationship between the lag analysis of recall transitions from early output positions shown in Figure 3 and the transitions as a function of serial position shown in Figure 2. Our goal is to re-express the advantage for neighbors of the initial presentation of the repeated item on recall initiation as a function of lag in a way that controls for the effects of recency and allows us to collapse across conditions.
Accordingly, we first calculated the difference between the renormalized PFR and the corresponding control renormalized PFR for each participant at each serial position. Before averaging across conditions, we divided each of these difference scores by the mean of the control renormalized PFR for that serial position. Because our interest was in comparing lags to each other, we only included data from participants who recalled at least one item with lag in the range −3 to +3 (inclusive) first in at least one of the experimental conditions. Our reasoning was that participants who did not contribute at least one recall initiation to the lag analysis did not convey any information about the relative probability of recalling items as a function of lag. At this stage of the analysis, 125 participants remained.
Finally, after averaging across conditions, we excluded outliers by removing any values for any lag that were more than four standard deviations from the mean. This excluded a total of four points across the six lags analyzed, one from lag −3, two from lag −2 and one from lag −1.
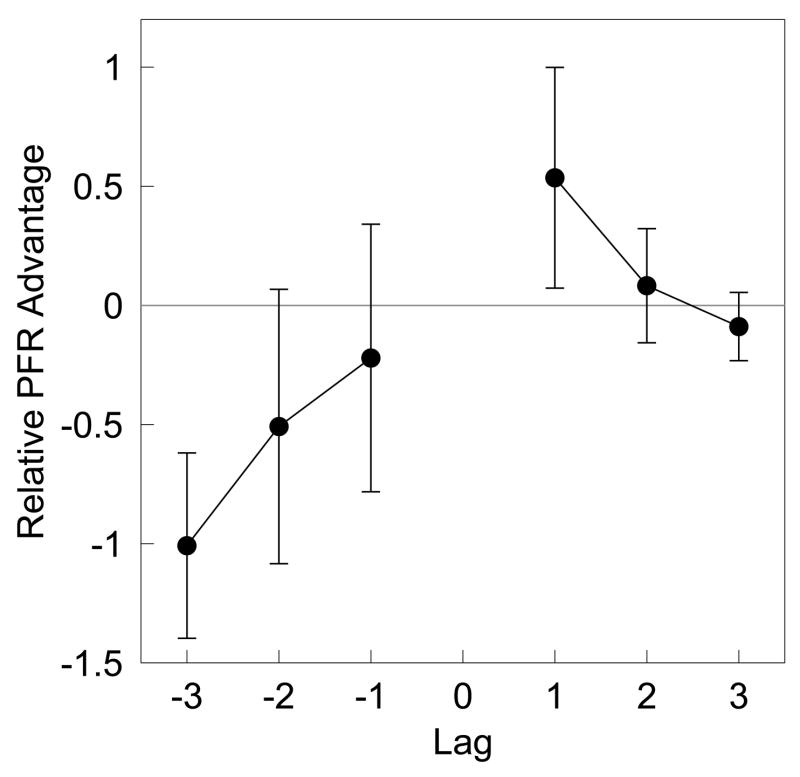
Figure 5 shows the results of the lag analysis collapsed across the X,10 conditions. It appears that there is an effect of lag to the initial presentation of the repeated item on the renormalized PFR, particularly in the forward direction. This impression was confirmed by a hierarchical linear regression of relative PFR advantage to lags in the forward direction (+1 to +3 inclusive). The mean slope in the forward direction was −.3 ±.1, t(124) = 2.45, p <.02. Considering the lags in the backward direction (−1 to −3, inclusive), the mean slope of a regression of relative PFR advantage to lag,.30 ±.16 did not quite reach significance, t(120) = 1.86, p =.065. However, the difference between the forward and backward slopes, taking into account the difference in sign was highly significant, t(120) = 2.96, p <.005. This last finding is particularly important because it indicates that the pattern of results could not be a consequence of a confound of lag with recency; although one might imagine recency producing an artifactual effect of lag in one direction or another, such an artifact would not go in opposite directions before and after the repeated item. The finding of different slopes in the forward vs backward direction indicate that the curve in Figure 5 is peaked around zero, strongly suggesting an associative effect of item repetition on recall initiation.
Figure 5.
Associative effects in initiation of immediate recall. The normalized difference in the PFR averaged over conditions 5,10 and 6,10 as a function of lag to the first occurrence of the repeated item. Error bars are 95% confidence intervals. See text for details.
General Discussion
Multiple mechanisms have been proposed to account for the recency effect in immediate free recall. Extant models based on sustained activation of end-of-list items in a short-term buffer (Atkinson & Shiffrin, 1968; Davelaar et al., 2005; Raaijmakers & Shiffrin, 1980) predict that temporally-defined associations should not contribute to recall initiation nor to the recall transitions at early output positions. In contrast, TCM (Howard & Kahana, 2002; Howard et al., 2006) predicts that temporally-defined associations should contribute to immediate recall in addition to the recency effect per se. We evaluated the qualitative predictions of these two types of models by comparing immediate recall in lists where an item from the middle of the list was repeated near the end of the list to immediate recall from control lists that did not contain a repeated item. If immediate recency is in fact associative, then we would expect an advantage for the neighbors of the initial presentation of the repeated item over the corresponding serial positions in control lists.
Counter to the predictions of buffer-based accounts of immediate recency, we observed associative effects in both recall transitions during immediate recency (Figure 2) and even in the initiation of immediate recall (Figure 4). When examined as a function of lag, the form of the associative effects observed in immediate recency (Figures 3 and 5) bore a strong resemblance to lag-CRPs observed in recall from long-term memory, which manifest both contiguity and an asymmetry effects (see Kahana et al., in press, for a review). This is consistent with the hypothesis that the same mechanisms that account for temporally-defined associations in recall from long-term memory are active in immediate recall.
Theoretical implications
The implications of the present study are quite clear—retrieval in immediate recency is influenced by temporally-defined associations. Buffer models of immediate recency (Davelaar et al., 2005; Kahana, 1996; Raaijmakers & Shiffrin, 1980; Sirotin, Kimball, & Kahana, 2005) predict that associative processes should not contribute to the early stages of immediate free recall. Although the present data are inconsistent with buffer models of immediate recency, it may be possible to elaborate these models to accommodate our findings. For example, one could propose that associative processes operate in establishing the occupancy of STS. That is, buffer models can handle associative effects in recall initiation if repetition of an item automatically recovers information its neighbors into STS. This recovery of other items into STS is reminiscent of the recovery of contextual information that is central to TCM. If this change were made to a buffer model, this would also lend itself to having a non-integral buffer capacity—or perhaps partial buffer occupancy. This is also reminiscent of TCM, which postulates a gradually-changing state of temporal context.
Another possibility is LTS contributes to the initiation of immediate free recall. This could explain the present findings if retrieval from LTS is associative, as hypothesized by the SAM model (Raaijmakers & Shiffrin, 1980). The contiguity effect observed in the lag-CRP, according to SAM is an associative process between recall of items in long-term memory (Kahana, 1996). However, in the hybrid model, items that are co-active in the buffer do not become associated with each other. Instead, contiguity effects in long-term memory are caused by a gradually changing context signal that serves to cue item recall. The context signal in the hybrid model evolves autonomously and independently of the items being recalled. That is, in the Davelaar et al. (2005) model, the lag-CRP from neither short-term nor long-term memory results from genuine associations between items, so that it cannot explain the present results as a consequence of contamination from LTS.
The present results were predicted by the theoretical framework offered by TCM. In TCM, temporal associations arise from the effect items have on the current state of temporal context, which serves as the cue for recall. In TCM, recall or repetition of an item retrieves the contextual elements that were part of nearby items’ encoding contexts. Because contextual drift is caused by retrieved context, temporally-defined associations should result from repetition of items within the list or recall of an item in the early stages of an immediate test. TCM predicts asymmetric temporally-defined associations at both early and late output positions in immediate free recall.
In TCM, asymmetry in temporally-defined associations is a natural consequence of the way in which items recover contextual states. When an item is repeated, the input it causes is composed of two associative components. One of these components is consistent with the effect the item had on the state of context when it was initially presented. These contextual elements persisted during list presentation so that they formed part of the contextual cue for items that followed the initial presentation of the repeated item. This accounts for the forward asymmetry in the lag-CRP. According to TCM the backward-going part of the lag-CRP is a consequence of the repeated item being bound to and subsequently recovering the contextual elements from its initial presentation. This recovered context overlaps with the contextual cue for items that preceded the initial presentation of the repeated item, resulting in a backward association. Because context changes gradually, the recovered contextual state also overlaps with the contextual cue for subsequent items, resulting in a symmetric retrieval cue. The effect of these different aspects of retrieved context have been extensively described elsewhere (Howard et al., 2005, 2006).
Whither short-term store
Atkinson and Shiffrin (1968) identified the contents of STS with the set of items currently being rehearsed. In this view, access to STS and the selection of which items to maintain is controlled by external strategic factors. For instance, Atkinson and Shiffrin (1968) described a number of different experiments using a continuous paired-associates task. These experiments were modeled using different rules for access to the buffer and different drop-out rules depending on the strategic pressures of the particular variant of the task. Attentional and strategic factors at study lead to effects on memory retrieval by modulating inter-item associations and associations to context (Raaijmakers & Shiffrin, 1980), or, more generally, the amount of information transferred to LTS (Atkinson & Shiffrin, 1968).
Studies of overt rehearsal (Brodie & Murdock, 1977; Rundus, 1971; Ward, Woodward, Stevens, & Stinson, 2003; Ward & Tan, 2004) have attempted to examine the contents of the rehearsal buffer by instructing participants to rehearse out loud during study. Overt rehearsal behaves very much like free recall itself. Laming (2006), in reanalyzing overt rehearsal data collected by Murdock and Metcalfe (1978), was able to predict the particular item recalled at multiple output positions in immediate free recall. Laming (2006) postulated that the process that gave rise to recall was similar to the process that gave rise to rehearsals and that subjects remembered the items in the order they were rehearsed. The fact that these assumptions were as successful as they were in predicting immediate free recalls suggests that rehearsal and free recall reflect similar retrieval mechanisms. While it is certainly the case that rehearsals have a causal effect on subsequent free recall, it is not at all clear that this necessitates postulating a memory store that “contains” the items in the current rehearsal set. Perhaps it is preferable to describe the rehearsal set as the output of memory retrieval that occurs during presentation of the study list. In this view, rehearsal, rather than reflecting the contents of a memory receptacle, is just free recall that happens during the list.
Davelaar et al. (2005) did not identify the contents of their short-term store with rehearsal. They did argue that properties of immediate free recall required a separate memory store based on sustained item activation. This activation-based short-term memory was contrasted with more lasting forms of memory which were identified with a weight-based memory. This parallel finds an analog in TCM, in which the current state of context can be seen as an activation-based representation of recent events (Howard et al., 2005) while the matrices enabling states of context to cue items can be seen as longer-lasting weight-based memory. Moreover, it is possible that TCM could describe characteristic effects from immediate free recall if equipped with a somewhat elaborated retrieval rule. Although the terminology used to describe buffer models and TCM are very different, if one identifies the state of the temporal context vector with STS there are really only two salient differences between the two. First, whereas items drop out of the buffer in a sudden all-or-none fashion, information decays gradually from the temporal context vector. Second, whereas an item always causes the same input to the buffer each time it is presented, the input to the temporal context vector caused by an item changes as it is repeated in different contexts.
Conclusions
Short-term buffer models of immediate recency propose that the first several recalls in immediate free recall simply reflect dumping of items from the buffer. We examined the role of associative processes in immediate recency using lists with an item from the middle of the list repeated at or near the end of the list. By closely examining recall transitions from early output positions and recall initiation we established that associative processes affect recall in immediate recency. These temporally-defined associations bear a strong resemblance to those observed in delayed free recall and continual-distractor free recall. These findings suggest that a unified account of recency across time scales, at least out to the scale of tens of seconds, remains a viable possibility.
Acknowledgments
The authors wish to acknowledge MH069938 to MWH and 2-MH55687 to MJK. Thanks to Aditya Datey for assistance with programming, to Bing Jing, Diana Hobbins, Donna Bridge, Tess Youker, and Michael Zaremba for data collection and to Paul Verhaeghen for helpful discussions. Send correspondence to Marc Howard, Syracuse University, 430 Huntington Hall, Syracuse, NY 13244-2340, marc AT memory DOT syr DOT edu.
Footnotes
The control lists also control for any encoding strategies participants might adopt in the middle serial positions as a consequence of noticing that some items are repeated.
One could argue that it would be more appropriate to include both serial positions as first members of the pairs in calculating the control measure. We chose to use only the second item to avoid contamination from putative long-term memory retrieval. We also conducted these control measures allowing first recalls from either of the repeated serial positions. This did not alter the conclusions.
If TCM is correct, then the effect of the context retrieved by the next-to-last item on recall initiation should be substantially less than the effect of the context retrieved by the last item on recall initiation. There is no reliable effect of the lag (relative to either of the repetitions of the item) on the PFR when the next-to-last item is repeated, consistent with what one would expect by reducing the signal-to-noise ratio. When one collapses over X,9 conditions and X,10 conditions, one gets essentially the same findings as reported here, albeit with more noise.
For the subjects we included, the first item was recalled first on a little less than.03 of the trials. Even for the 14 subjects we excluded for initiating recall at the first serial position above.10, they started recall with the first item on only 21% of trials. The infrequency of adopting a serial recall strategy means that it cannot have a substantial bearing on whether immediate recency reflects a dump from STS on the vast majority of trials.
Contributor Information
Kenneth A. Norman, Department of Psychology, Princeton University
Michael J. Kahana, Department of Psychology, University of Pennsylvania
References
- Anderson JR, Bower GH. Recognition and retrieval processes in free recall. Psychological Review. 1972;79(2):97–123. [Google Scholar]
- Atkinson RC, Shiffrin RM. Human memory: A proposed system and its control processes. In: Spence KW, Spence JT, editors. The psychology of learning and motivation. Vol. 2. New York: Academic Press; 1968. pp. 89–105. [Google Scholar]
- Bjork RA, Whitten WB. Recency-sensitive retrieval processes in long-term free recall. Cognitive Psychology. 1974;6:173–189. [Google Scholar]
- Brodie DA, Murdock BB. Effects of presentation time on nominal and functional serial position curves in free recall. Journal of Verbal Learning and Verbal Behavior. 1977;16:185–200. [Google Scholar]
- Brown GDA, Neath I, Chater N. A ratio model of scale-invariant memory and identification unpublished manuscript. [Google Scholar]
- Davelaar EJ, Goshen-Gottstein Y, Ashkenazi A, Haarmann HJ, Usher M. The demise of short-term memory revisited: empirical and computational investigations of recency effects. Psychological Review. 2005;112(1):3–42. doi: 10.1037/0033-295X.112.1.3. [DOI] [PubMed] [Google Scholar]
- Estes WK. Statistical theory of spontaneous recovery and regression. Psychological Review. 1955;62:145–154. doi: 10.1037/h0048509. [DOI] [PubMed] [Google Scholar]
- Friendly M, Franklin PE, Hoffman D, Rubin DC. The Toronto Word Pool: Norms for imagery, concreteness, orthographic variables, and grammatical usage for 1,080 words. Behavior Research Methods and Instrumentation. 1982;14:375–399. [Google Scholar]
- Glanzer M. Storage mechanisms in recall. In: Spence KW, Spence JT, editors. The psychology of learning and motivation. New York: Academic Press; 1972. pp. 129–193. [Google Scholar]
- Glenberg AM, Bradley MM, Stevenson JA, Kraus TA, Tkachuk MJ, Gretz AL. A two-process account of long-term serial position effects. Journal of Experimental Psychology: Human Learning and Memory. 1980;6:355–369. [Google Scholar]
- Greene RL. Sources of recency effects in free recall. Psychological Bulletin. 1986;99:221–228. [Google Scholar]
- Healy AF, Parker JT. Serial position effects in semantic memory: Reconstructing the order of U. S. presidents and vice presidents. In: Roediger HL, Nairne JS, editors. The nature of remembering: Essays in honor of Robert G. Crowder. Washington, DC: American Psychological Association; 2001. pp. 171–188. [Google Scholar]
- Howard MW, Fotedar MS, Datey AV, Hasselmo ME. The temporal context model in spatial navigation and relational learning: Toward a common explanation of medial temporal lobe function across domains. Psychological Review. 2005;112(1):75–116. doi: 10.1037/0033-295X.112.1.75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard MW, Kahana MJ. Contextual variability and serial position effects in free recall. Journal of Experimental Psychology : Learning, Memory, and Cognition. 1999;25:923–941. doi: 10.1037//0278-7393.25.4.923. [DOI] [PubMed] [Google Scholar]
- Howard MW, Kahana MJ. A distributed representation of temporal context. Journal of Mathematical Psychology. 2002;46(3):269–299. [Google Scholar]
- Howard MW, Kahana MJ, Wingfield A. Aging and contextual binding: Modeling recency and lag-recency effects with the temporal context model. Psychonomic Bulletin & Review. 2006;13:439–445. doi: 10.3758/bf03193867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard MW, Youker TE, Venkatadass V. The persistence of memory: Contiguity effects across several minutes. doi: 10.3758/pbr.15.1.58. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahana MJ. Associative retrieval processes in free recall. Memory & Cognition. 1996;24:103–109. doi: 10.3758/bf03197276. [DOI] [PubMed] [Google Scholar]
- Kahana MJ, Howard M, Polyn S. Associative processes in episodic memory. In: Roediger HL, editor. Learning and memory - a comprehensive reference. in press; Elsevier; [Google Scholar]
- Kahana MJ, Howard MW, Zaromb F, Wingfield A. Age dissociates recency and lag-recency effects in free recall. Journal of Experimental Psychology : Learning, Memory, and Cognition. 2002;28:530–540. doi: 10.1037//0278-7393.28.3.530. [DOI] [PubMed] [Google Scholar]
- Laming D. Testing the idea of distinct storage mechanisms in memory. International Journal of Psychology. 1999;34(56):419–426. [Google Scholar]
- Laming D. Predicting free recalls. Journal of Experimental Psychology : Learning, Memory, and Cognition. 2006;32(5):1146–1163. doi: 10.1037/0278-7393.32.5.1146. [DOI] [PubMed] [Google Scholar]
- Mensink GJM, Raaijmakers JGW. A model for interference and forgetting. Psychological Review. 1988;95:434–55. [Google Scholar]
- Murdock BB. The distinctiveness of stimuli. Psychological Review. 1960;67:16–31. doi: 10.1037/h0042382. [DOI] [PubMed] [Google Scholar]
- Murdock BB. The serial position effect of free recall. Journal of Experimental Psychology. 1962;64:482–488. [Google Scholar]
- Murdock BB, Metcalfe J. Controlled rehearsal in single- trial free recall. Journal of Verbal Learning and Verbal Behavior. 1978;17:309–324. [Google Scholar]
- Murdock BB, Okada R. Interresponse times in single- trial free recall. Journal of Verbal Learning and Verbal Behavior. 1970;86:263–267. [Google Scholar]
- Nairne JS, Neath I, Serra M, Byun E. Positional distinctiveness and the ratio rule in free recall. Journal of Memory and Language. 1997;37:155–166. [Google Scholar]
- Neath I, Brown GDA. SIMPLE: Further applications of a local distinctiveness model of memory. In: Ross BH, editor. The psychology of learning and motivation. San Diego, CA: Academic Press; 2006. [Google Scholar]
- Neath I, Crowder RG. Schedules of presentation and temporal distinctiveness in human memory. Journal of Experimental Psychology : Learning, Memory, and Cognition. 1990;16:316–327. doi: 10.1037//0278-7393.16.2.316. [DOI] [PubMed] [Google Scholar]
- Raaijmakers JGW. The story of the two-store model of memory: Past criticisms, current status, and future directions. In: Meyer D, Kornblum S, editors. Attention and performance. xiv. Cambridge, MA: MIT Press; 1993. pp. 467–488. [Google Scholar]
- Raaijmakers JGW, Shiffrin RM. SAM: A theory of probabilistic search of associative memory. In: Bower GH, editor. The psychology of learning and motivation: Advances in research and theory. Vol. 14. New York: Academic Press; 1980. pp. 207–262. [Google Scholar]
- Rundus D. An analysis of rehearsal processes in free recall. Journal of Experimental Psychology. 1971;89:63–77. [Google Scholar]
- Sirotin YB, Kimball DR, Kahana MJ. Going beyond a single list: Modeling the effects of prior experience on episodic free recall. Psychonomic Bulletin & Review. 2005;12:787–805. doi: 10.3758/bf03196773. [DOI] [PubMed] [Google Scholar]
- Talmi D, Grady CL, Goshen-Gottstein Y, Moscovitch M. Neuroimaging the serial position curve: A test of single-store versus dual-store models. Psychological Science. 2005;16(9):716–23. doi: 10.1111/j.1467-9280.2005.01601.x. [DOI] [PubMed] [Google Scholar]
- Thapar A, Greene RL. Evidence against a short-term- store account of long-term recency effects. Memory & Cognition. 1993;21:329–337. doi: 10.3758/bf03208265. [DOI] [PubMed] [Google Scholar]
- Ward G, Tan L. The effect of the length of to-be-remembered lists and intervening lists on free recall: a reexamination using overt rehearsal. Journal of Experimental Psychology : Learning, Memory, and Cognition. 2004;30(6):1196–210. doi: 10.1037/0278-7393.30.6.1196. [DOI] [PubMed] [Google Scholar]
- Ward G, Woodward G, Stevens A, Stinson C. Using overt rehearsals to explain word frequency effects in free recall. Journal of Experimental Psychology : Learning, Memory, and Cognition. 2003;29(2):186–210. doi: 10.1037/0278-7393.29.2.186. [DOI] [PubMed] [Google Scholar]
- Watkins MJ, Neath I, Sechler ES. Recency effect in recall of a word list when an immediate memory task is performed after each word presentation. American Journal of Psychology. 1989;102:265–270. [PubMed] [Google Scholar]
- Yntema DB, Trask FP. Recall as a search process. Journal of Verbal Learning and Verbal Behavior. 1963;2:65–74. [Google Scholar]