Time and Frequency Characteristics of Purkinje Cell Complex Spikes in the Awake Monkey Performing a Nonperiodic Task

Abstract

A number of studies have been interpreted to support the view that the inferior olive climbing fibers send periodic signals to the cerebellum to time and pace behavior. In a direct test of this hypothesis in macaques performing nonperiodic tasks, we analyzed continuous recordings of complex spikes from the lateral cerebellar hemisphere. We found no periodicity outside of a 100-ms relative refractory period.

INTRODUCTION

Several kinds of evidence motivate hypotheses that propose clock-like behavior of the inferior olive (IO) (for review, see Kitazawa and Wolpert 2005). First, clinical disorders involving IO can lead to pathologic tremors (Albin 1998; Deuschl and Wilms 2002; Rieder et al. 2003). Second, oscillatory membrane potentials of individual IO neurons have been repeatedly observed in vitro (Bal and McCormick 1997; Lampl and Yarom 1993, 1997; Llinas and Yarom 1981, 1986), although in many preparations they occur only 10% of the time. Third, in acute animal experiments, the drug harmaline induced tremor as well as periodic IO cellular discharges, linking the structure and function together (DeMontginy and Lamarre 1975; Headley et al. 1976; Lamarre et al. 1971; Llinas and Volkind 1987; Weiss 1982). Fourth, in a few experiments in awake moving animals, complex spikes (CSs) generated by IO have at times been noted to be periodic (Armstrong and Rawson 1979; Bloedel and Ebner 1984; Gellman et al. 1985; Lang et al. 1996; Llinas and Sasaki 1989). Nevertheless, these conclusions are based foremost on single-cell signaling of IO neurons in anesthetized animals, decerebrate animals, or tissue slice preparations (Benardo and Foster 1986; Bloedel and Ebner 1984; Chorev et al. 2007; Lang et al. 1996, 1997; Llinas and Sasaki 1989; Sasaki et al. 1989; Sugihara et al. 1995; Welsh et al. 1995).

In awake performing animals, single-cell recordings are for the most part inconsistent and contradictory in supporting the periodic clock hypothesis. Only in studies of Lang et al. (1999) was there occasional periodic IO discharge during rest periods in awake rats. S. S. Smith (1998) noted task-related periodic Purkinje cell CS activity in awake walking rats but no such periodic discharge during rest periods. Keating and Thach (1995, 1997) noted “no clock-like activity” in the CS output of Purkinje cells in monkeys performing nonperiodic tasks. What is the frequency of complex spikes during behavior? Does this frequency change over time or is it fixed? Is periodicity (when observed) transient or persistent? Is the phase of the periodicity time locked to a task or to a universal clock signal? None of the mentioned studies that claim existence of IO periodicity provide statistics on the characteristics of these periodicities. We addressed these questions with a variety of new quantitative and statistical analyses to characterize complex spike firing during normal behavior in awake trained macaques. We found no periodicity as such during these conditions.

METHODS

Animal task

Surgical and experimental procedures were in accordance with National Institutes of Health and U. S. Department of Agriculture guidelines and were approved by the Animal Studies Committee at Washington University School of Medicine. The experiments were originally designed for studies of visuo-motor adaptation and learning tasks and took place in three different experiments conducted by three different experimenters (authors BG, SN, and JK). The data presented here are from the same animals for which data were presented in the previous reports. We retrospectively looked back at the database of all such recordings and identified any continuous recording that had available CSs, irrespective of the animal performance on the tasks. The spike times were then exported to text files for further analysis.

Three rhesus monkeys (A, B, and C) were trained on one of two different types of visuo-motor response tasks: tasks 1 or 2. In task 1 (previously described in Greger et al. 2004), during each trial, the animal (monkey A or B) was visually cued to make a rapid natural reach movement from an initial hold position (with both hands on the handles of our apparatus) to a visual target and to return immediately to the original on-hold hands-on-apparatus position before being rewarded. In task 2 (previously described in Keating and Thach 1995), the animal (monkey C) was trained to track a visual target on a screen using flexion extension wrist movements. Several weeks prior to any recording, each monkey was fitted (under full anesthesia) with a recording chamber and head bolts. Each recording included many individual trials under different visuo-motor adaptation paradigms described previously (see also Norris 2004) as well as the intervening non-task-related periods; all were recorded in a continuous fashion. The time intervals were randomized between the start of consecutive trials, movement prompts, and reward delivery as previously described. The tasks therefore contained no inherent periodicity. Some of the data from monkey C (task 2) were previously included in a subset of recordings published by Keating and Thach (1995). Here we only used recordings that were made continuously (not from concatenated segments as previously reported).

Animal data collection

Single-unit recordings were made stereo-tactically from the right lateral cerebellar lobe of the monkeys in a head-restrained system. Each cell was individually identified and monitored throughout each recording session based on the shape of simple and CS wave forms as viewed on an oscilloscope (see Greger et al. 2004; Norris et al. 2004).

In task 1, the signals from the electrodes were amplified, filtered, and digitally recorded for local off-line analysis. The digitally recorded waveforms were converted to spike time points by template matching (performed by independent runs for simple spikes and CSs) using Cambridge Electronic Design's Spike2 software. In task 2, the CSs were identified using window filtering before the spike times were digitally recorded using Spike2 software. For all recordings, the spike times and the experimental parameters were stored on digital storage media. Additionally, for many of the recordings in task 1, the digitized high-resolution full electrical potential wave-forms were also stored for subsequent verification. We were concerned that the isolation of action potentials might vary across time. To be certain that potential variations in isolation did not bias our results and conclusions, we analyzed all units that were digitally marked in different ways (see Fig. 1), classified them into types I–VI (see Table 1) and compared the results. In sum, potential variability in isolation did not support exceptions to the main conclusions.

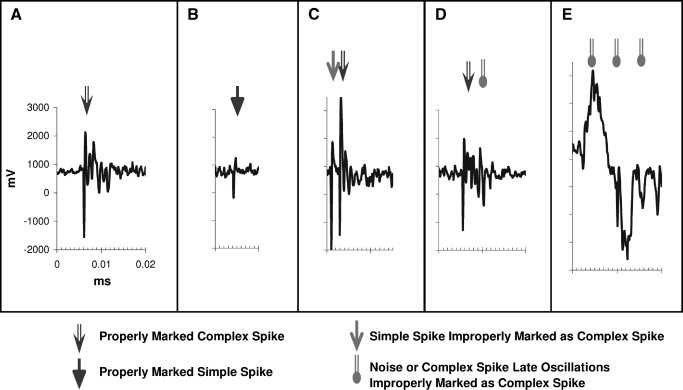
FIG. 1.

Examples of Single Unit Potential Waveforms. Plots show examples of appropriately marked (and miss-marked) Complex Spikes. A simple spike example is also included. All plots are made on the same scale. A: shows the scaling bars, an example of a good Complex Spike waveform properly identified. B: an example of a properly identified Simple Spike. C: an example of a miss-marked Complex Spike. The detection algorithm properly identified the second Complex Spike, but erroneously also identified the preceding Simple Spike as a Complex Spike (presumably because of size of the waveform, background noise, and oscillations from the following Complex Spike). D: an example of a Complex Spike double marked because of the noise in the oscillations. E: an example of background noise marked as Complex Spikes (there may be Simple Spikes hidden in the noise).

TABLE 1.

Categories of auto-correlograms observed among the CS recordings

Cell Type	Cells Counts				Description
		Animal				Total
	A	B	C
Type I	26	3	9	38	No peaks within the first 100 ms. The rest of each auto-correlogram is very uniform.
Type II	5	7	4	16	Some early (<20 ms) peaks, followed by a trough up to 100 ms. The rest (above 100 ms) appear uniform.
Type III	20	3	0	23	A large early peak (often in the first 5 ms bin), followed by a period of reduced baseline up to the 100 ms. Beyond the 100 ms region appear uniform.
Type IV	8	5	10	23	Auto-correlogram peaks within the first 0–50 ms followed by a gradual decline in the baseline auto-correlogram.
Type V	14	5	9	28	Auto-correlograms looks very uniform for the entire 5 second time span.
Type VI	9	11	5	25	Reduced Baseline Auto-correlograms (but not zero) up to 100 ms, followed by a uniform baseline.
Not Classified	4	1	9	14	Auto-correlograms were too sparse for us to judge their shapes, or (in one case) results appeared clearly erroneous.
Total	86	35	46	167

Descriptions of different categories of auto-correlograms observed among the CS recordings. See Figures (2) and (4) for pattern summaries.

Basic spike statistics

For each recording, we calculated the recording length, total spike count, mean, median, maximum and minimum interspike intervals, and instantaneous firing rates. We then plotted the instantaneous firing rates and interspike intervals as a function of time (firing rate profiles). Additionally, we produced interspike interval histograms and instantaneous firing rate histograms for each recording. These basic statistics were used for verification of spike events, comparisons of event profiles, and evaluation of the fidelity of recordings across time.

Autocorrelogram analysis

One-sided spike time autocorrelograms of individual spike trains were computed using custom software with 5-ms binning intervals and 1,024 bins (up to just over a 5-s time lag). Zero time lag (self-spike interaction) peaks were not included. The binning was done with respect to each reference spike time after the autocorrelogram function was calculated (the data were not prebinned) to minimize a prebinning artifact. Note that the selected 5-ms bin size is smaller than the 7 ms expected duration of a CS. The autocorrelogram computations were verified using data with known autocorrelogram peaks and by comparison with the Spike2 software's built-in autocorrelogram function. For comparison and reporting purposes, we normalized (scaled) the y axis of the autocorrelograms by dividing each autocorrelogram by its corresponding recording length and scaled the autocorrelograms by one over the bin size (1/0.005 s.). The x axis was not scaled. Fast Fourier transform (FFT) of each cell's autocorrelogram was calculated and the results were verified using data with known frequency and using FFT functions from other commercial software packages.

Time-frequency spectral analysis (Gabor transform)

The Gabor transform (Bastiaans 1981; Gabor 1946) characterizes the power spectrum of a signal as a function of time. It is similar to applying a Fourier transform repeatedly to sequential fixed length segments of data. However, because it is done in the complex domain (accounting both for amplitude and phase), it accounts for phase and history of spike occurrences. More precisely, the Gabor transform is a time-dependent Gaussian windowing procedure (wavelet) applied to the Fourier transform that results in fixed interval and slightly overlapping wavelets. It transforms the signal recorded in the time domain into smaller fixed-size time segments. Then it performs a frequency spectral analysis at each time segment interval while preserving signal phase characteristics with respect to an absolute recording time. It is defined by the equation

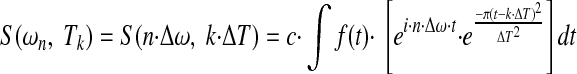(1)

where the entire recording period T_total for a time dependent function f(t) is broken up into K many equal ΔT segments at T_k intervals, and the entire frequency spectrum is broken into N many equal Δω segments at ω_n intervals. The constant c is a scaling constant. The parameters ΔT and Δω are inversely related to one another by the relationship: Δω = 2·π/ΔT. The discretized version of this equation when each spike event is treated as a Dirac delta function at time t_j results in

(2)

In contrast to the Gabor transform, the complete Fourier transform fully projects a time-dependent signal into the frequency domain at a frequency resolution related to the total recording length. Instead of projecting a signal from time domain into frequency domain en block, the Gabor transform (as in Eqs. 1 and 2) breaks the signal into conjoint time-frequency segments at fixed step sizes of ΔT and Δω intervals. The time-dependent information is at the cost of frequency resolution by a factor of k = T_total/ΔT. Other wavelet based methods use related techniques for breaking up a data set into conjoint time frequency segments using different windowing methods and/or various time and/or frequency sampling periods (e.g., using a variable step size ΔT and proportionately sizing Δω).

We used custom software for performing the analysis described by Eq. 2 and verified our analysis using data with known frequencies (neural and simulations). The theoretical upper frequency limit (Nyquist limit) for these neural recordings is not particularly meaningful. The actual time resolution of the electrical waveforms from which spike times were calculated was >10 kHz. Because CSs seem to have a mean interspike interval of ∼1 s and an average action-potential duration of 7 ms, the higher end of our frequency spectrum has little practical meaning. Nevertheless we included frequency spectrum data ≤100 Hz for demonstration purposes (this will become clear in the following text). We computed the results using a 5.0-s sampling interval in one trial (ΔT = 5 s., Δω = 0.2 Hz) as well as a 2.0-s sampling interval (ΔT = 2 s., Δω = 0.5 Hz) on a second run (i.e., the spectrum data were calculated for each 2.0- or 5.0-s block of data at each 2.0- or 5.0-s intervals). These window size choices were based on the low firing rates of CSs (with mean interspike time difference of 1 to 2 s), which require larger windows to capture any periodicity in a meaningful way, the use of autocorrelograms in our analysis to adequately explore the local temporal features of our signal at intervals <5.0 s, and our interest in exploring frequency properties of the signal within the 10-Hz range with a frequency resolution of <1.0 Hz in keeping with previous reports.

The result of the Gabor transform calculated in this way is a series of complex numbers as a function of frequency at each sampled time point. Therefore for each conjoint time-frequency data point, we have both spectral amplitude as well as phase. We could therefore further analyze the signal in various ways looking at time-frequency distribution or even evolution of the signal.

For our data, the sparseness of CS events, even within the larger 5.0-s time window, made any conjoint three-dimensional time-frequency spectral analysis plots of the signal meaningless. Across time, the power fluctuated too much and, per 5.0-s epoch, usually remained around noise levels. In other words there were many 5-s windows where only one or two spike events occurred in them as would be expected from a natural Poisson process with a 1-spike/s mean event rate.

In the frequency domain, there are different ways of summarizing, across time the power-spectrum distribution of the signal. One way is to look at the mean power distribution in each of the Gabor transform sampling time windows, using averaging to make-up for the weak signal amplitude. Thus we calculated a per-time-segment or per-epoch power spectrum as a function of the sampling time (ignoring the phase). We then looked at the average per epoch power spectrum across the entire duration of each recording. We calculated this value and called it the ISUM (for independent sums). Note that ISUM signals that have different phases across different epochs, such as transient periodicities of weak amplitude, will be quite noticeable.

Another way of summarizing the power distribution is to look at the distribution of power in the entire recording en block, much the same way as a complete Fourier transform of the signal would. We achieved this more efficiently (albeit at a frequency resolution cost) by summing the complex Gabor transform terms for each frequency across time. We converted this value to the amplitude of the power terms. Finally, this power distribution was normalized for the total recording length by dividing the power over time. We called this the CSUM (for complex sum). Note that in CSUM, unlike ISUM, signals that have the same frequency but different phases across epochs will largely cancel each other out.

For each of our recordings we calculated the ISUM and CSUM for both sizes of sampling windows of 2.0 and 5.0 s. Note that ISUM is sensitive to recurring weak periodicities of various phases, such as one would expect from a particular task dependent periodic signal generator. Alternatively, the CSUM is sensitive to weak periodicities with a fixed phase such as one would expect from a true clock.

RESULTS

Results overview

Figure 1 represents the digital marking of the analog wave forms of complex and simple spikes (A and B) and possible artifacts (C–E), and Table 1 summarizes the classification scheme of these marked recordings. Figure 2, H–M, shows the autocorrelograms of individual recordings thus marked and classified. Figure 3 depicts one representative recording and the steps in its analysis. We isolated CS data from a total of 167 Purkinje cells. In the first section in the following text, we present the temporal characteristics of CSs. Most of this analysis is focused on the examination of inter-spike intervals and autocorrelation of CSs. In the second section, we present the spectral characteristics of the same recordings. Using the various analyses we were unable to detect periodicity in any one of the recorded neurons.

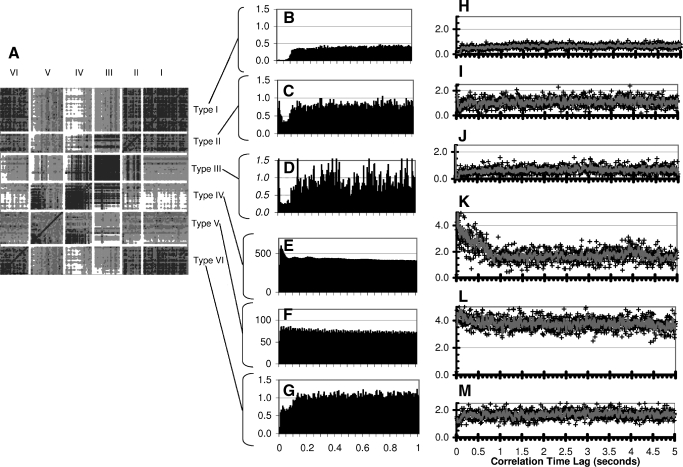
FIG. 2.

Shape Similarity Comparison among Auto-correlograms A: results of cluster Analysis of the Auto-correlograms based on 1-r Pearson correlation using a complete linkage analysis method. The diagonal dark line is the line of identity (recording compared to itself). Auto-correlograms were corrected only for the total recording length before comparison. For each small square, darker shading reflects higher similarity in a comparison pair. The recordings are sorted along each axis, first based on our assigned autocorrelation type, and then by the median Complex Spike Instantaneous Firing Rate. Blank areas are placed between the types for easier visualization. B–G: average of all auto-correlograms in each classification type. H–M: each panel shows examples of one type of auto-correlogram using our classification. For clarity, examples are chosen from longer recordings with more sample points. Each marked point represents the amplitude of scaled auto-correlogram peak at that latency. The line represents a smoothing of each adjacent four data points to help visualize the results (given our small bin size of 5 ms). H: type I example shows no activity during 100 ms refractory period. I: type II and J: type III have early transient peaks, then a 100 ms refractory period followed by flat correlation regions. Type II and III differ by amplitude of the early peak and activity during the first 100 ms. K: type IV recordings have a very short refractory period followed by a gradual decent in the autocorrelogram up to 1 s or longer. L: type V recordings have a flat baseline and no notable 100 ms refractory period. M: type VI recordings have a decrease overall amplitude up to 100 ms refractory period followed by a flat area above the 100 ms refractory region.

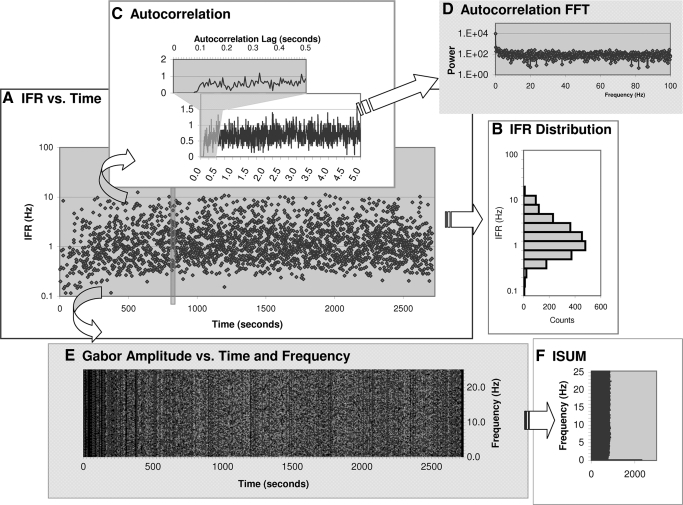
FIG. 3.

An Example of Analysis Steps. Each recording was analyzed individually with regards to both temporal and spectral structure. This figure is an example of a Type I cell. A: Instantaneous Firing Rate (IFR)—on a log-scale—is plotted vs. recording time. Note that the recording contained little data before the 1200-s mark. B: a histogram of IFR distribution (also on log scale). C: scaled (for recording length and bin-size) auto-correlogram of the spike times. Recording time is from the first to the last spike time occurrence, which in this recording excludes the period of inactivity up to the 1200-s mark. Inset shows the period before 0.5 s in greater detail. D: Fourier transform of auto-correlogram in (C). E: amplitude of the Gabor transform for each frequency and time step using a 5.0 s time window. Lighter shading reflects higher amplitudes. For the DC term the amplitude is the number of spikes occurring in that time step. Due to space limitation this plot only shows the results up to 25 Hz. The phase of the Gabor transform and the remainder of frequencies up are computed but not plotted. F: ISUM (sum of Gabor amplitudes for each frequency) from D is plotted on a log amplitude scale.

CS temporal firing profile group characteristics

Some notable trends emerged among each of the recording type classes. Recordings of the cells with best signal isolation (Fig. 1, A–C) as well as the group average demonstrated a mean autocorrelogram per bin spike count of 0.5 and a relative refractory period of 100 ms before the first recorded autocorrelogram spike. After the 100 ms lack of autocorrelogram peak activity, the remainder of each autocorrelogram was quite uniform, even ≤5 s.

We had anticipated these autocorrelographic findings (the 100-ms early trough and the lack of periodicity) from the interspike interval (ISI) histograms and the instantaneous firing rate histograms of our spike data.

Analysis of differences among CS temporal firing profiles

Because we had the digitized single-unit recording waveforms of full recorded electrical events for many of our cells, we could go back and look for the sources of the early bin events in the autocorrelograms and ISI distribution profile for various cells belonging to various classification types. For every available case, we looked back at the raw electrical waveform for every pair of spikes with an ISI interval of <20 ms. We also reviewed a sampling of recorded CSs from those cells judged best isolated (Fig. 1, A–C). In total, we identified >3,500 such short-latency repeat spike events among 35 recordings (representing 4.5% of all complex spikes in those 35 representative recordings). Figure 1 shows several such examples, along with examples of higher quality simple and complex spikes. In this analysis, every repeat spike event marking in a pair that occurred at a time of <10 ms reflected an erroneous double marking of the normal oscillations within the same CS waveform (for example Fig. 1D) or a simple spike preceding a CS and marked as a earlier CS (Fig. 1C).

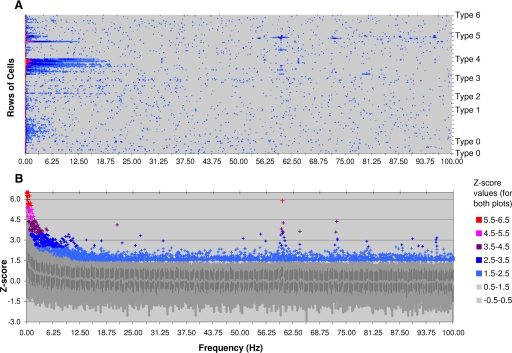
FIG. 4.

Fast Fourier Transform (FFT) results from all the autocorrelograms. A FFT was computed and then normalized for each recording individually. For comparison purposes, the normalization is done first, by taking the logarithm of the Power of the auto-correlogram FFT. For Each log-Power-FFT we calculated the mean and standard deviation above the DC term. These results are used to compute the Z-score (number of standard deviations from the mean) for each log-Power-FFT with respect to its own power spectrum. A: in this panel the Z-scale values for each auto-correlogram-FFT is plotted vs. frequency. Each row along the y-axis represents a different recording. The recordings are sorted by Type (I–VI and 0 for unclassified), and then by highest to lowest mean firing rates (from top to bottom). Note that 60 Hz noise is most identifiable in Type IV and V cells. Also, note a smearing of higher z-scores around 10 Hz in only one Type V recording. B: statistical plot of the same data as in (A). Frequency is marked along the x-axis as before. The y-axis shows the distribution of z-scores among all the recordings for each frequency. The heavy line in the middle shows the median z-scores for each frequency. The shaded bars and area show the 0, 20, 80, and 99 percentile regions, respectively, from low to high. Individual z scores greater than 2.5 standard deviations and above 99 percentile are individually plotted using the same color coding scheme as in A. Note the correspondence of individual outlier values to the recordings in A.

Spectral analysis via autocorrelogram FFTs

We computed FFT of each individual autocorrelogram (Fig. 4). For comparison across recordings, each cell's FFT power spectrum was converted to a log scale and normalized on a z-scale (number of SDs from the mean log power above DC term with respect to its own log power mean and SD excluding DC). Figure 4A shows the complete normalized power spectrums from all the cells in our recordings plotted on a z scale. Figure 4B shows the per frequency distribution of 95% of z-score values and the outliers, comparing the z scores among all recordings. As can be seen in the figures, depending on the classification type, most of the power in these recordings is localized to the DC portion, or in a continuum from the DC portion into low frequency regions. The power spectra appear uniform and without any dominant frequency terms across most of the recordings.

Spectral analysis via Gabor transforms

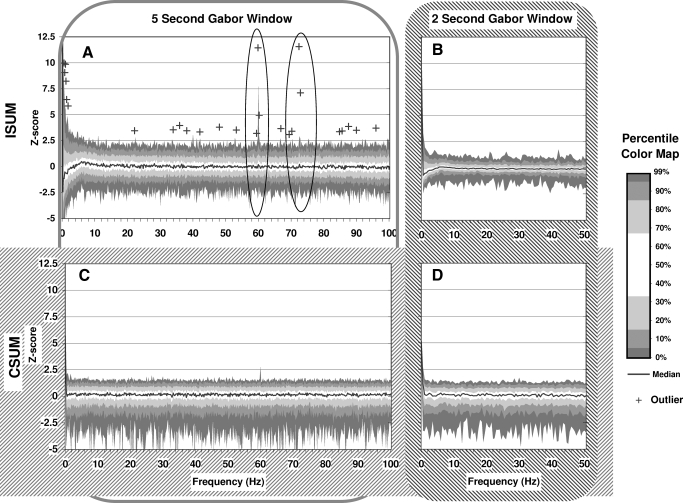
While the autocorrelograms looked at recurrent fixed interval relationships among the spikes in a spike train, the Gabor transform data allowed the analysis of the frequency components across time (Fig. 5). Again, these results are summarized in different ways looking for recurrent periodicities of various phases (via ISUM) or recurrent periodicities of fixed phase (via CSUM) for different time windows. For each cell, we had four summarized Gabor spectral plots: the ISUM and CSUM, each calculated once at 2.0- and once at 5.0-s time windows. For comparison across cells, we normalized the power spectra from individual recordings in a manner similar to that used above when normalizing autocorrelogram FFT on a log-power z scale. This normalized the peak-by-peak variability of each power-spectrum plot to its own overall variability and baseline power. We then compared all the normalized power spectra by looking at the distribution of spectral peaks at each frequency point from among all recordings. Figure 5 summarizes these results. Similar to the autocorrelogram FFT plots, the only notable peaks occur at 60 Hz and for the ISUM plot at 75 Hz.

FIG. 5.

Gabor Transform Distribution of Frequencies. Gabor transform summaries for all recordings were calculated and are plotted in four different ways (A, B, C, and D). For each recording, Gabor transforms were calculated using both 2.0 s (A and C) and 5.0 s time windows (B and D). For each window size, the results were summarized by summing the values of Gabor transforms across time, once by summing the amplitudes (ISUM, A and B) and once summing the complex value Gabor transform results (CSUM, C and D) before converting results to amplitudes. For comparison, the Gabor transform resulting ISUM and CSUM power spectrum plots were normalized to their own baseline log-power on a Zscale similar to auto-correlogram FFT plots. The Z-score percentile plots (A individual outliers) are plotted here comparing individual frequency terms across all recordings.

In summary, using the Gabor transform direct spectral analysis, similar to the FFT analysis of autocorrelograms, we still saw no evidence of a physiological cerebellar clock even for long observation periods.

DISCUSSION

What makes a true clock a clock is not mere transient periodicity but rather its fixed phase and fixed frequency properties. In the circadian rhythm and the menstrual cycles of mammals, there exist well-timed, endogenous periodic signals. Thus true biological clocks of even several daylong periodicities exist. However, one has to demonstrate and clarify the spectral characteristics of any periodicity before making claims regarding its nature and characteristics. We have performed such analyses on IO signals as measured in the CS of PCs. In our recordings, during nonperiodic tasks (to avoid correlational confounds), we saw no evidence of any physiological CS periodic discharge. Our results held true for all recordings, measured using both the autocorrelographic method and the direct spectral Gabor transform method. These data provide evidence in awake monkeys performing a nonperiodic task that CS activity does not display any intermittent or continuous periodic discharge patterns.

Our data contrast with other reports mentioned in the introduction that have noted persistent or rest period periodic IO discharges. The study by S. S. Smith (1998) is also consistent with our data, showing no periodic IO discharge during rest periods. Additionally, during the Smith stepping task, the frequency of IO discharge depended on the task. This task-dependent change in IO activity is consistent with other published results (Kim et al. 1987; Lamarre and Puil 1974).

The physical explanation for the 10- to 12-Hz periodicity that many authors have observed thus in our view remains open and conjectural. Many published results hint at the fact that a 10-Hz IO discharge is not a preferred discharge frequency of these neurons but rather their maximal saturated frequency response. Armstrong and Rawson (1979), recording in awake but inactive cats, reported occasional high-frequency bursts of “as many as eight [CSs] in 1 s,” but these high rates only lasted 1–2 s and “autocorrelograms revealed no longer term regularity or rhythmicity.” Gellman et al. (1985) noted only rare 10-Hz discharge rates from sensory provoked IO neurons: “olivary cells generally responded only to the transient phase of a stimulus. Thus repeated stimulation evoked repeated responses provided that the 100-ms refractory period was respected.” These reports suggest then that a 10- to 12-Hz periodicity may be the maximal firing rates of these neurons. The corresponding 80- to 100-ms refractory period is notable in our data and data published by numerous other authors (Keating and Thach 1995; Lang et al. 1997, 1999; Llinas and Sasaki 1989; Llinas and Volkind 1987; Sasaki et al. 1989), where its duration seems to be closer to 80 ms in some anesthetized preparations. In our data, we clearly observe a 100-ms refractory period in type I cells, but also note it in type II, III, and VI cells as well.

It may be that the 10-Hz firing response rates of these neurons is reflective of the saturation kinetics of the IO neurons with a 100-ms refractory period. The idea that reaching saturation kinetics of a neuron based on its refractory period may lead to false periodicity in autocorrelograms is not new (Bar-Gad et al. 2001). An additional piece of evidence supporting this hypothesis is in observations by Llinas and Sasaki (1989). The preparation they used included anesthetized rats that were further treated with Harmaline, a known producer of IO rhythmicity. When these presumably maximally driven cells (under nonphysiological circumstances) were further stimulated, they could only produce further spikes in phase with the stimulation. More interestingly, stimulations out of phase with the rhythmic patterns of these neurons delayed the onset of the next rhythmic burst pattern. This suggests that stimulations during the refractory periods prolonged the refractory periods even further, preventing further spike occurrence. Thus one may expect 10- to 12-Hz IO periodicity during periods of increased overall stimulation and firing.

A candidate driving IO 10-Hz periodicity may be extrinsic inputs that either push IO to its maximal firing because of a 100-ms refractory period or are inherently from periodic sources such as a rhythmically firing thalamus. The two main inputs to IO include an excitatory pathway via mesendiancephalic region and an inhibitory input via deep cerebellar nuclei. Ruigork and Voogd (1995) demonstrated that stimulation at the mesendiancephalic junction produces, first, a short-latency action potential in IO, followed—in >50% of cases—by a second, long-latency action potential at a delay of between 120 and 300 ms. Although a 100-ms refractory period may explain the significant delay in the occurrence of the second spike, it does not explain why it occurs long after the input has been withdrawn. Furthermore, Lang (2001) reported that obstruction of this excitatory pathway via local blockade of glutamatergic synaptic transmission in IO paradoxically enhanced IO periodicity, while, not unexpectedly, reducing its overall firing rate. In another paper, Lang et al. (1996) reported that blockade of cerebellar nuclear originated GABAergic input increased the firing rate of these neurons while also enhancing their periodicity but at a lower frequency of 5–6 Hz. While these observations hint that periodicity of IO membrane potential is at least partly an inherently local intrinsic phenomenon, a simultaneous double blockade experiment (for both excitatory and inhibitory pathways) has not been reported.

Moreover, a 100-ms refractory period does not explain the lower (5–6 Hz) discharge frequencies. Llinas and Yarom (1981) concluded that IO oscillations are due to intrinsic conductance or connectivity (via gap junctions) of IO neurons. They later (Llinas and Yarom 1986) demonstrated the propensity of IO neurons to oscillate at two different frequency regions, one driven by depolarizing currents at a lower frequency of ∼6 Hz and another driven by hyper-polarizing currents at a frequency of ∼10–12 Hz. They concluded that IO oscillatory behavior was due to local ionic conductance and local gap junctions, which allowed the periodicity to persist and even be quantized into local domains. Welsh and Llinas (1997) suggested this was a “pace-making” signal for activating synergistic muscle groups. Smith (1998) also concluded that the task-dependent periodicity of IO is, in fact, the evidence for the role of this pace maker in timed motor behavior. The term pace-maker, even more than the term clock, suggests that in the view of these authors, IO periodicity is akin to cardiac pace-maker cells in the sino-atrial node, although with two preferred frequencies. Therefore one should expect to find either a preferred modulated frequency of these neurons, such as in the range of the two frequency regimes found by Llinas and Yarom (1986), or a select un-modulated, fixed, preferred frequency during normal physiological function of IO (as would be necessary for coupled oscillator models). We, however, see no evidence of IO output periodicity in our data that would support either of these two conclusions, even at the lower 5- to 6-Hz frequency range.

The 80- to 100-ms refractory period between IO-generated CSs may reflect some interesting dynamics of the olivo-cerebellar circuit. The time window of cerebellar LTD appears to be most significant within 0–100 ms between parallel fiber activity and the occurrence of a complex spike (Karachot et al. 1994). Learning of timing in rabbit eye-blink conditional response (presumably via the same circuitry) also only takes place up to a 100-ms interstimulus delay (Schneiderman and Gormezano 1964; Smith et al. 1969). A 150-ms lag appears to exist between increased simple spike activity and before the arrival of a complex spike (Miall et al. 1998). It is as though the circuit is built to inherently avoid producing a second spike after the occurrence of an IO generated spike to avoid interference with the time window for plasticity. Such a system may require intrinsic memory of 100 ms to keep account of any important signals that arrive while it is in a refractory cycle. The late activated long latency action potential that Ruigork and Voogd (1995) observed in IO might be the signature of this intrinsic memory mechanism. In fact, the more curious question is how this system avoids oscillations despite its strong substrate for doing so? Similar arguments can be extended to synchrony as well. Note, if multiple IO units fired synchronously, large areas of the cerebellar cortex and nuclei (which incidentally would be most related to the task being executed) would become nonfunctional at once. Recent computational work suggests that olivary gap junctions may synchronize the input rather than the neuronal output, limiting the potential IO influence on synchronizing complex spike activity (Kistler and De Zeeuw 2005). This circuit may therefore have an intrinsic need to be de-synchronized, rather than synchronized, and to avoid oscillations to remain functional. Indeed Schweighofer et al. (1999) used a modeling paradigm to demonstrate that cerebellar gap junctions may indeed de-synchronize IO neurons. A timing device may still be at work but as a 100-ms time keeper built to avoid dysfunctional performance or learning.

What we conclude from these data is that under the normal physiological conditions of awake animals performing nonperiodic tasks, IO firing is not periodic. This may not necessarily preclude IO from having transient task-related periodicities such as during maximal firing response or during periodic tasks (such as in walking, Smith 1998). We draw this conclusion despite other observations that IO neurons in vitro appear to have at least a potential to oscillate at two preferred frequencies of 5–6 and 10–12 Hz. These in vitro oscillations do not have a clear functional significance, and future work is necessary to understand these nonphysiologic properties of the IO.

GRANTS

This research was funded by National Institute of Neurological Disorders and Stroke Grant R01 NS-12777.