Calcium Dynamics and Vasomotion in Arteries Subject to Isometric, Isobaric, and Isotonic Conditions

Abstract

In vitro, different techniques are used to study the smooth muscle cells' calcium dynamics and contraction/relaxation mechanisms on arteries. Most experimental studies use either an isometric or an isobaric setup. However, in vivo, a blood vessel is neither isobaric nor isometric nor isotonic, as it is continuously submitted to intraluminal pressure variations arising from heart beat. We use a theoretical model of the smooth muscle calcium and arterial radius dynamics to determine whether results may be considerably different depending on the experimental conditions (isometric, isobaric, isotonic, or cyclic pressure variations). We show that isobaric conditions appear to be more realistic than isometric or isotonic situations, as the calcium dynamics is similar under cyclic intraluminal pressure variations (in vivo-like situation) and under a constant pressure (isobaric situation). The arterial contraction is less pronounced in isotonic than in isobaric conditions, and the vasoconstrictor sensitivity higher in isometric than isobaric or isotonic conditions, in agreement with experimental observations. Interestingly, the model predicts that isometric conditions may generate artifacts like the coexistence of multiple stable states. We have verified this model prediction experimentally using rat mesenteric arteries mounted on a wire myograph and stimulated with phenylephrine.

INTRODUCTION

The regulation of hemodynamics by variations of the arterial diameter results from the contraction of smooth muscle cells (SMCs) present in the muscular arterial wall. The SMC contraction is due to an increase in the cytosolic calcium concentration (1–4), and calcium increases result from the presence of vasoconstrictors. Vasomotion consists of cyclic diameter variations of muscular arteries or arterioles that are not a consequence of heart beat, respiration, or neuronal input, but result from calcium oscillations in the SMCs (5–8).

A blood vessel is continuously exposed to intraluminal pressure variations arising from heart beat. In vivo, a vessel is therefore neither submitted to constant pressure ( i.e., isobaric conditions), nor to constant radius (i.e., isometric conditions), nor to constant tension (i.e., isotonic conditions). However, most in vitro experimental studies on calcium dynamics, contraction/relaxation mechanisms, and vasomotion of arterial segments make use either of an isobaric (9–11) or an isometric (6,12,13) setup. These setups allow to control, respectively, the intraluminal pressure and measure arterial diameter variations, or to control the arterial diameter and measure tension or pressure variations. Experiments can be performed either on wire-mounted (wire myograph) or pressurized cannulated arterial preparations.

Tanko et al. (14,15) and VanBavel and Mulvany (16) report an enhanced vascular sensitivity to vasoconstrictor during isometric compared to isobaric loading on pressurized cannulated arterial segments. Similarly, on arterial rings mounted on a wire myograph, McPherson (17) found that vascular reactivity to the α-adrenoceptor agonist methoxamine was significantly higher under isometric than under isobaric or isotonic conditions. In addition, the maximum response to methoxamine, in terms of diameter change, was always greater under isobaric than under isotonic conditions.

The aim of this study is to analyze, theoretically, whether there may be important differences in the results (calcium dynamics, contraction, and vasomotion of arteries) depending on the kind of experimental conditions: isometric, isobaric, or isotonic. We have previously developed a model describing the calcium dynamics of a coupled population of SMCs and the resulting arterial diameter variations (18). This model is used here to perform a bifurcation analysis of the mean SMC calcium concentration and vessel radius in the isometric, isobaric, and isotonic cases. We compare these cases to a more in vivo-like situation where the artery is exposed to cyclic pressure variations. The differences in the results arising from these various conditions are analyzed and compared to experimental results in the literature. Moreover, an experiment with rat mesenteric arteries mounted on a myograph and stimulated with increasing and decreasing concentrations of phenylephrine (PE) is performed to confirm a model prediction under isometric conditions, for which no experimental comparison has been found in the literature.

METHODS

Mathematical model

The model is composed of equations describing the mean SMC calcium dynamics, the smooth muscle stress development, and the vessel radius dynamics. All model equations are taken from our previous article (18) and are briefly discussed here.

Calcium dynamics

The SMC calcium dynamics is described by five variables: the calcium concentration in the cytosol c, the calcium concentration in the sarcoplasmic reticulum s, the cell membrane potential v, the open-state probability w of calcium-activated potassium channels, and the IP₃ concentration I:

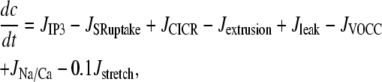(1)

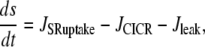(2)

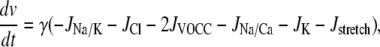(3)

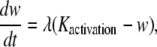(4)

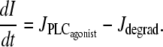(5)

The precise expressions of the various terms appearing in this set of nonlinear differential equations are given in the Appendix. The term J_stretch, modeling stretch-activated channels (SACs), is given by

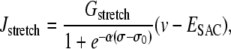(6)

where G_stretch is the whole-cell conductance for SACs, E_SAC the SAC reversal potential, α the slope of stress dependence of the SAC activation sigmoidal, and σ₀ the half-point of the SAC activation sigmoidal. The arterial wall stress σ is written differently depending on the conditions studied (see below). SACs increase the cytosolic calcium level by promoting a direct influx of extracellular calcium (Eq. 1) and by depolarizing the SMCs (Eq. 3), which leads to a calcium influx through voltage-operated calcium channels. The coefficient 0.1 of in Eq. 1 takes into account that calcium is a divalent ion and carries ∼20% of the total SAC current (19).

An increase in the SMC vasoconstrictor concentration is simulated by an increase of the agonist-activated phospholipase C (PLC) rate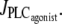

Active stress dynamics

Calcium and force development in SMCs are related by the cross-bridge phosphorylation and latch state model of Hai and Murphy (20). In this model, an elevated calcium level induces a contraction through the formation of cross bridges between actin and myosin filaments. There are four possible states for myosin: free nonphosphorylated cross bridges (M); free phosphorylated cross bridges (Mp); attached phosphorylated cross bridges (AMp); and attached dephosphorylated latch bridges (AM). The dynamics of the fraction of myosin in a particular state is given by

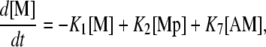(7)

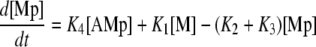(8)

(9)

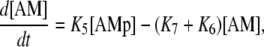(10)

where the rate constants K_n (n = 1, …, 7) regulate the phosphorylation and bridge formation. The only nonconstant parameter K₁ ≡ K₆ is related to the cytosolic calcium concentration

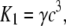(11)

where γ is a constant characterizing the sensitivity of the contractile apparatus to calcium. Active stress is directly proportional to the fraction of attached cross bridges [AM] + [AMp].

Vessel radius dynamics

The vessel radius is computed by considering the equilibrium of tangential forces in the wall (Laplace law): σ = pr/h = σ_p + σ_a + σ_v, where p is the intraluminal pressure; r is the inner vessel radius; h is the vessel wall thickness; σ_p is the elastic stress; σ_a is the active stress; and σ_v is the viscous stress. Viscous stress is given by σ_v = ηdr/dt, where η is the wall viscosity coefficient. The time evolution of the inner vessel radius r is then given by (21)

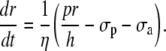(12)

Depending on the value of the radius, the expressions for σ_p are (21)

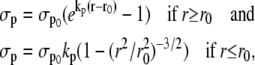(13)

where r₀ is the unstressed radius. Active stress σ_a is directly proportional to the fraction of attached cross bridges [AM] + [AMp], and is dependent on the vessel external radius (21)

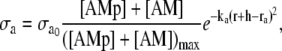(14)

where 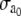is the maximal active stress and ([AMp] + [AM])_max the maximal fraction of attached cross bridges. The expression for the wall thickness h is written by assuming that the wall is incompressible and the vessel length constant, i.e., the wall volume, is assumed constant (22):

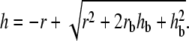(15)

Isobaric conditions

Isobaric conditions are generated using a fixed pressure p. With Laplace law σ = pr/h, the term J_stretch modeling SACs is given by Koenigsberger et al. (18) as

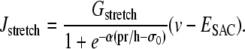(16)

Isometric conditions

Isometric conditions are generated by fixing the arterial radius, i.e., by setting Eq. 12 to zero: 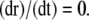The term J_stretch modeling SACs is then given by

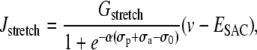(17)

where the vessel radius r is a fixed parameter in terms σ_p (Eq. 13) and σ_a (Eq. 14).

Isotonic conditions

Isotonic conditions are generated by fixing the arterial tension T = pr (Laplace law). Eq. 12 is then written as

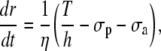(18)

where the wall tension T is a constant. The term J_stretch modeling SACs is then given by

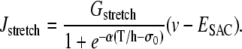(19)

Cyclic pressure variations

In vivo, the pressure is subject to cyclic variations arising from heart beats. This is modeled by considering sinusoidal pressure p variations

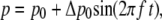(20)

where p₀ is the mean pressure, Δp₀ the oscillation amplitude, and f the oscillation frequency. These cyclic pressure variations arise in term J_stretch (Eq. 16) and in Eq. 12. The meanings and values of all parameters are given in Tables 1 and 2.

TABLE 1.

Parameter values for the SMC model

Parameter	Description	Value
F	Maximal rate of activation dependent calcium influx.	0.23 μM/s
Kr	Half saturation constant for agonist-dependent calcium entry.	1 μM
GCa	Whole cell conductance for VOCCs.	0.00129 μM mV−1 s−1
vCa1	Reversal potential for VOCCs.	100.0 mV
vCa2	Half-point of the VOCC activation sigmoidal.	−24.0 mV
RCa	Maximum slope of the VOCC activation sigmoidal.	8.5 mV
GNa/Ca	Whole cell conductance for Na+/Ca2+ exchange.	0.007 μM mV−1 s−1
cNa/Ca	Half-point for activation of Na+/Ca2+ exchange by Ca2+.	0.5 μM
vNa/Ca	Reversal potential for the Na+/Ca2+ exchanger.	−30.0 mV
B	SR uptake rate constant.	2.025 μM/s
cb	Half-point of the SR ATPase activation sigmoidal.	1.0 μM
C	CICR rate constant.	55 μM/s
sc	Half-point of the CICR Ca2+ efflux sigmoidal.	2.0 μM
cc	Half-point of the CICR activation sigmoidal.	0.9 μM
D	Rate constant for Ca2+ extrusion by the ATPase pump.	0.08 s−1
vd	Intercept of voltage dependence of extrusion ATPase.	−100.0 mV
Rd	Slope of voltage dependence of extrusion ATPase.	250.0 mV
L	Leak from SR rate constant.	0.025 s−1
Gstretch	Whole cell conductance for SACs.	0.0061 μM mV−1 s−1
ESAC	Reversal potential for SACs.	−18 mV
α	Slope of stress dependence of the SAC activation sigmoidal.	0.0074 mmHg−1
σ0	Half-point of the SAC activation sigmoidal.	500 mmHg
γ	Scaling factor relating net movement of ion fluxes to the membrane potential (inversely related to cell capacitance).	1970 mV/μM
FNa/K	Net whole cell flux via the Na+-K+-ATPase.	0.2 μM/s
GCl	Whole cell conductance for Cl− current.	0.00134 μM mV−1 s−1
vCl	Reversal potential for Cl− channels.	−25.0 mV
GK	Whole cell conductance for K+ efflux.	0.002 μM mV−1 s−1
vK	Reversal potential for K+.	−94.0 mV
λ	Rate constant for net KCa channel opening.	45.0
cw	Translation factor for Ca2+ dependence of KCa channel activation sigmoidal.	0 μM
β	Translation factor for membrane potential dependence of KCa channel activation sigmoidal.	0.13 μM2
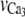	Half-point for the KCa channel activation sigmoidal.	−27.0 mV
RK	Maximum slope of the KCa activation sigmoidal.	12.0 mV
k	Rate constant of IP3 degradation.	0.1 s−1

TABLE 2.

Parameter values for contraction

Parameter	Description	Value
K2	Rate constant for phosphorylation and bridge formation.	0.5 s−1
K3	Rate constant for phosphorylation and bridge formation.	0.4 s−1
K4	Rate constant for phosphorylation and bridge formation.	0.1 s−1
K5	Rate constant for phosphorylation and bridge formation.	0.5 s−1
K7	Rate constant for phosphorylation and bridge formation.	0.1 s−1
([AMp] + [AM])max	Maximal fraction of attached cross bridges.	0.8
γ	Phosphorylation coefficient.	17 μM−3s−1
η	Viscosity coefficient.	10 mmHg s
σp0	Elastic stress.	0.0191 mmHg
kp	Elastic coefficient.	0.15 μm−1
r0	Unstressed radius.	50 μm
σa0	Maximal active stress.	1.8 · 105 N/m2
ka	Muscular coefficient.	0.0006 μm
ra	Optimal radius for active stress.	95 μm
rb	Basal radius.	56.3 μm
hb	Basal thickness.	15 μm
p0	Mean pressure.	100 mmHg
Δp0	Pressure oscillation amplitude.	20 mmHg
f	Pressure oscillation frequency.	1 Hz

Numerical methods

The model equations were solved using a fourth-order Runge-Kutta method. The software AUTO implemented in XPPAUT (23) was used for bifurcation diagrams. All stable solutions indicated by AUTO have been found in our numerical simulations.

Experimental methods

Isometric force measurement

Male Sprague-Dawley rats aged 6–10 weeks, and weighing 200–350 g were obtained at the animal house of the University of Geneva and treated in agreement with the Care of Animals (edited by “l'Académie Suisse des Sciences Médicales” and “la Société Hélvétique des Sciences Naturelles”). Rats were anesthetized with 2-bromo-2-chloro-1,1,1-trifluoroethane (halothane), and then the neck was disrupted. The mesentery was isolated and a first-order mesenteric artery was dissected from the mesenteric vascular bed. The blood vessel was cleaned of surrounding tissues and cut to obtain a ring of 2 mm length in a buffered Krebs solution (at room temperature) of the following composition (mM): NaCl 118.7, KCl 4.7, CaCl₂ 2.5, MgSO₄ 1.2, KH₂PO₄ 1.2, NaHCO₃ 24.8, D-glucose 10.1, pH 7.4 and aerated with 95% O₂ and 5% CO₂ gas mixture. The ring was incubated for isometric tension recording in a Mulvany microvessel Myograph (Multimyograph, model 610 M, Danish Myo Technology A/S, Aarhus, Denmark). The stainless steel organ bath had a volume of 5 ml. It contained warmed (37°C) and oxygenated (95% O₂, 5% CO₂) Krebs-Ringer buffer. The ring was threaded on two stainless wires (40 μm diameter). One of the wires was connected to the lever of a force-displacement transducer to record the isometric force developed by the ring. Recorded data were digitized with an analog-digital interface (MacLab, World Precision Instrument, Sarasota, FL) and then stored on the hard disk of a MacIntosh compatible computer. A commercially available and validated software program (MacLab System, World Precision Instrument) was used to analyze these data.

Study design

A passive resting tension of 0.3 mN was initially applied and the rings were allowed to stabilize for 45 min. The incubation bath was perfused at 20 ml/min with an increasing concentration of PE from 0 to 100 μM then a decreasing concentration from 100 to 0 μM PE. This concentration gradient was built up in the following manner. A conic flask (Erlenmeyer) containing 590 ml of 100 μM PE in Krebs solution was connected by polyethylene tubing to a cylindrical bottle containing 900 ml Krebs solution without PE continuously mixed with a magnetic stirrer. A peristaltic pump pumped in this bottle the solution for bath perfusion. By communicating vessels principle, the solution level was the same in the Erlenmeyer and in the cylinder. Thus, the PE solution progressively flowed into the cylinder. This creates an exponential increase of PE concentration in the cylinder and consequently in the bath. Then the system was inverted, and the perfusion solution was pumped in the Erlenmeyer that contained 100 μM PE. This solution was then progressively diluted by the Krebs solution coming from the cylinder.

RESULTS AND DISCUSSION

Isometric, isobaric, and isotonic conditions

Bifurcation diagrams

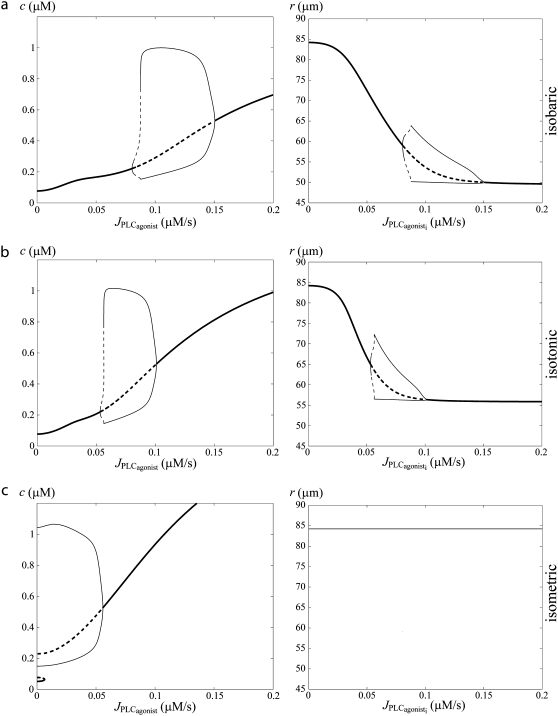
Fig. 1 a gives bifurcation diagrams of the cytosolic calcium concentration c and of the vessel radius r with respect to the agonist-activated PLC-rate, 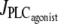in isobaric conditions (constant pressure p = 80 mmHg). At low values of 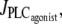i.e., at low vasoconstrictor concentration, the cytosolic calcium level is in a stable steady state (domain I). Increasing the vasoconstrictor concentration, the calcium concentration and the vessel contraction increase, and a Hopf bifurcation occurs: the steady state becomes unstable and the calcium level begins to oscillate, giving rise to an oscillating radius, thus vasomotion (domain II). The mean calcium level and the oscillation frequency essentially become higher and the mean radius smaller with increasing values of 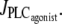Note that for a small range of 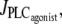the branch of periodic orbits is unstable. This unstable part is delimited by period doubling bifurcations, and period doubling solutions are found for the corresponding small range of 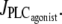Finally, the diagram of Fig. 1 a has another Hopf bifurcation from which the steady state becomes stable again (domain III). The cytosolic calcium level is high and no longer oscillates, and the radius is constant and small.

FIGURE 1.

Bifurcation diagrams of the calcium concentration c (left column) and the vessel radius (right column) with respect to the agonist-activated PLC-rate, 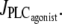(Thick solid line) Stable rest state; (thick dashed line) unstable rest state; (thin solid line) minima and maxima of stable oscillations; and (thin dashed line) minima and maxima of unstable oscillations. (a) Isobaric case (the constant pressure p = 80 mmHg corresponds to that of the isometric and isobaric cases at 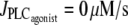). (b) Isotonic case (the constant tension T = pr corresponds to that of the isometric and isobaric cases at 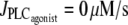). (c) Isometric case (the constant radius r = 84.225 μm corresponds to that of the isobaric and isotonic cases at ).

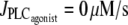Fig. 1, b and c, gives the corresponding bifurcation diagrams in isotonic and isometric conditions, respectively. In this figure, the radii in the absence of vasoconstrictor are the same, i.e., the isometric radius is chosen in order that the isometric circumferential stress equals the isobaric and isotonic stress pr/h = T/h at 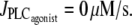The differences of the bifurcation diagrams arising from different conditions (isobaric, isotonic, or isometric) are discussed below.

Vasoconstrictor sensitivity

The calcium level is higher and the three domains of Fig. 1 are shifted to the left in isometric with respect to isobaric or isotonic conditions. In isobaric preparations, the vessel contraction after a vasoconstrictor concentration rise diminishes the circumferential stress pr/h. This reduces the SAC conductance (Eq. 16), decreasing the direct calcium influx through SACs and the calcium influx through voltage-operated calcium channels (VOCCs) because of a smaller cell depolarization. In isotonic conditions, the stress T/h also slightly decreases with a rise in the vasoconstrictor concentration, since the arterial thickness increases during contraction (Eq. 15). In the isometric case, there is no such counterregulatory mechanism after an increase in the vasoconstrictor concentration. Indeed a vasoconstrictor concentration elevation significantly increases the active stress σ_a and thus the total stress, thereby enhancing the calcium influx through SACs. This leads to a higher vasoconstrictor sensitivity and a lower vasoconstrictor concentration threshold necessary for vasomotion in isometric conditions. This is in agreement with the experimental observations of Tanko et al. (14), VanBavel and Mulvany (16), and McPerson (17) reporting an enhanced vascular sensitivity to vasoconstrictor in isometric compared to isobaric or isotonic conditions. Thus, higher vasoconstrictor concentrations should be used to induce vasomotion in isobaric and isotonic conditions. Note that in the isotonic case, the three domains of Fig. 1 are also slightly shifted to the left with respect to the isobaric case. Starting from identical initial conditions at 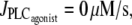the isotonic stress T/h becomes actually higher than the isobaric stress pr/h at a given vasoconstrictor concentration, since T is a constant and r decreases with increasing vasoconstrictor concentrations.

Contraction amplitude

The mean contraction is less pronounced in isotonic than in isobaric conditions, i.e., the mean arterial radius is smaller at a given vasoconstrictor concentration (compare panels b and c in Fig. 1). This result is in agreement with the experimental findings of McPherson (17). In our model, this is a consequence of the fact that at a given nonzero vasoconstrictor concentration, term T/h in Eq. 18 is higher than term pr/h in Eq. 12.

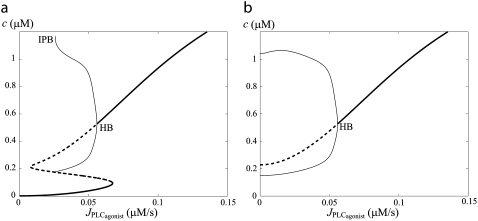
Multistability

Under isometric conditions, several stables states may coexist at a given vasoconstrictor concentration (multistability, see Fig. 1 c at 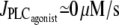). Depending on the radius value, this multistability is more or less pronounced or even absent. Fig. 2 gives bifurcation diagrams of the cytosolic calcium concentration with respect to the agonist-activated PLC-rate, 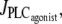at two different radius values in isometric conditions. The branch of periodic orbits emanates from an infinite period bifurcation (Fig. 2 a), and terminates via a Hopf bifurcation. Note that, in Fig. 2 b, domain I does not exist (no multistability); i.e., for this radius value, vasomotion is always obtained in the absence of vasoconstrictor.

FIGURE 2.

Bifurcation diagrams of the calcium concentration c with respect to the agonist-activated PLC-rate, 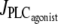in isometric conditions. (Thick solid line) Stable rest state; (thick dashed line) unstable rest state; (thin solid line) minima and maxima of stable oscillations; (thin dashed line) minima and maxima of unstable oscillations; (HB) Hopf bifurcation; and (IPB) infinite period bifurcation. (a) r = 77.205 μm. (b) r = 86 μm.

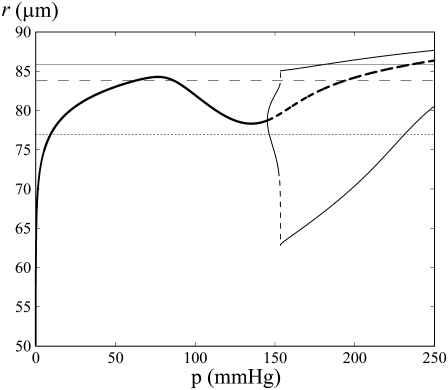
This multistability can be explained intuitively by considering the radius dynamics with respect to pressure at a fixed vasoconstrictor concentration (see Fig. 3). At low pressure, the radius increases with pressure. For a certain pressure range, the radius decreases with increasing pressure, a phenomenon called the myogenic response. The myogenic response is often obtained experimentally and has been first observed by Bayliss (24). The radius decreases when active stress σ_a dominates the term pr/h in Eq. 12. This is caused by a significant increase in the open probability of the SAC (and thus the calcium level) after a pressure increase. At high pressure, the radius increases again with pressure. Indeed, the open probability of the SAC is then nearly one, resulting in low calcium and σ_a variations after a pressure increase. The dominant term in Eq. 12 becomes again pr/h, causing a radius increase. A vessel presenting a myogenic response has the property that multiple values of pressure or circumferential stress pr/h correspond to a given radius value r and vasoconstrictor concentration (Fig. 3). Therefore, several states of calcium concentration may coexist in isometric conditions. In Fig. 1 c and Fig. 2, a and b, the solutions of the bifurcation diagram at 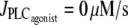correspond to the ones given by the intersection of the horizontal dashed line (for Fig. 1 c), the dotted line (for Fig. 2 a), and the shaded line (for Fig. 2 b) with the branch of solutions in Fig. 3. Experimentally, one would then expect to observe different behaviors at a given vasoconstrictor concentration depending on the initial conditions. Note that there is no multistability if the vessel presents no myogenic response, i.e., if the conductance of the SACs is small.

FIGURE 3.

Bifurcation diagram of the vessel radius r with respect to pressure in the absence of vasoconstrictor (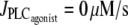). The intersections of the branch of solutions with the horizontal dashed, dotted, and shaded lines give the solutions of the bifurcation diagram at 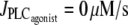for Fig. 1 c and Fig. 2, a and b, respectively.

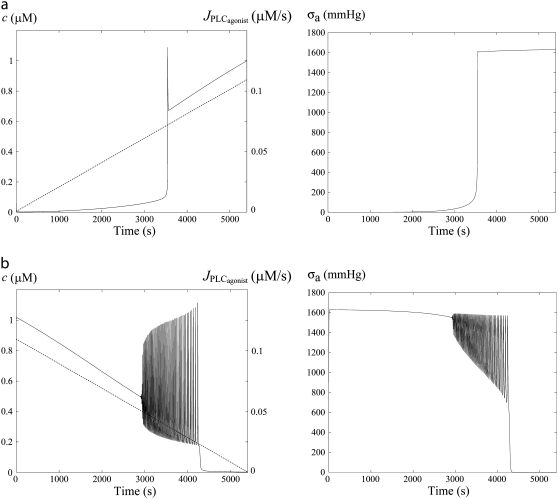
Fig. 4 gives the time evolution of the SMC calcium concentration c and active stress σ_a during a continuous linear vasoconstrictor concentration change (increase of 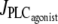from 0 to 0.11 μM/s in Fig. 4 a and decrease of 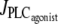from 0.11 to 0 μM/s in Fig. 4 b) at a fixed radius of r = 77.205 μm (same radius value than in Fig. 2 a). Note that the active stress σ_a rapidly reaches its maximal value due to a saturation of the fraction of attached cross bridges. Indeed, increases of the calcium concentration exceeding ∼0.8 μM no longer result in active stress σ_a variations. Such high calcium concentration variations that do not bring about stress and radius variations have been observed experimentally (8). In this figure, the multistability manifests itself as a sudden steep calcium increase (Fig. 4 a) or decrease (Fig. 4 b). Such a discontinuity or sudden steep increase in a concentration-response curve has also been observed experimentally (Fig. 6 of (16)). Note that on Fig. 4 a the vasomotion domain of Fig. 2 a has been missed due to the coexistence of stable and oscillatory states. Indeed, at 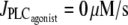the calcium concentration is in domain I (no multistability), and stays on the same branch after an increase in 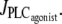When this branch becomes unstable, the calcium concentration directly jumps to domain III. In Fig. 4 b, the vasoconstrictor concentration is linearly decreased, allowing us to obtain the vasomotion domain. Indeed, the calcium concentration is initially in domain III, and stays on the same branch after a decrease in 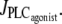A stable branch of periodic orbits is emanating from this branch via a Hopf bifurcation (see Fig. 2 a). When this branch of periodic orbits terminates, the calcium concentration jumps to the stable steady-state branch (domain I). This result suggests that experimentally existing vasomotion domains may be missed in isometric conditions when performing concentration-response curves. Different vessel radius values and the effects of a vasoconstrictor concentration increase and decrease should be studied to ensure that a possible vasomotion domain has not been missed.

FIGURE 4.

Time evolution of the SMC calcium concentration (left column, solid curve) and active stress (right column) during a continuous vasoconstrictor concentration change (left column, dotted line) at a fixed radius of r = 77.205 μm (same radius as in Fig. 2 a). (a) The agonist-activated PLC-rate, 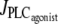is increased linearly from 0 to 0.11 μM/s. (b) 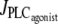is decreased linearly from 0.11 to 0 μM/s.

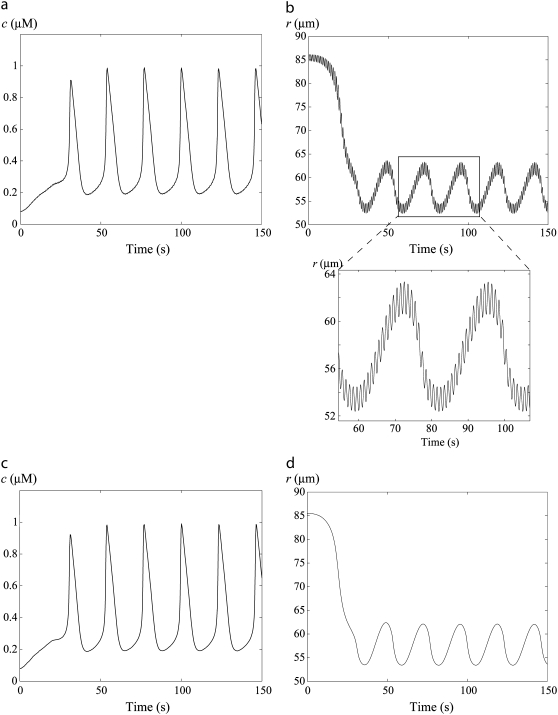
FIGURE 6.

Time evolution of the SMC calcium concentration (a and c) and the vessel radius r (b and d) at 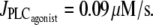In panels a and b, the pressure is subject to sinusoidal variations with a mean value of p₀ = 100 mmHg. In panels c and d, the pressure is kept constant at 100 mmHg. The simulations start from the equilibrium state of the vessel in the absence of vasoconstrictor.

On vessels where the myogenic response is less pronounced, which may be the case in presence of endothelium (18), the domain of multistability and thus the probability of missing a vasomotion domain become smaller. This result may also provide an explanation why, in some experimental studies, vasomotion is not observed in isometric conditions in the absence of endothelium (6,12,13).

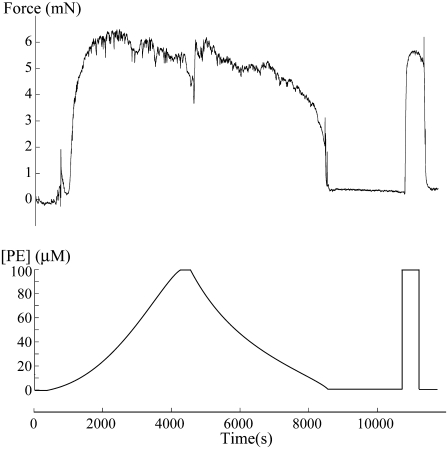
We have performed an experiment to confirm the model prediction that concentration response curves under isometric conditions are different if the vasoconstrictor concentration is increased or decreased (Fig. 5). Four out of four experiments with a rat mesenteric arterial ring mounted on a myograph showed a sudden steep increase in isometric force during a continuous PE concentration increase. During the PE concentration decrease, the shape of the isometric force curve was different with a smoother decrease (n = 4), as predicted previously by the model (Fig. 4). Note that, just before the PE decrease, there is a change in the vessel tone resulting from the interruption of the pump. All experiments (n = 4), therefore, showed the expected different time evolution of the isometric force during a PE increase or decrease. However, only one vessel exhibited vasomotion, and this vasomotion occurred in the ascending and not in the descending part of the curve. In the model, the existence and the location of the vasomotion domain is dependent on the isometric radius value chosen (compare Fig. 1 c and panels a and b of Fig. 2), and on our particular choice of model parameters (18). Indeed, changes in some parameters can shift the vasomotion domain (18,25).

FIGURE 5.

Isometric force measurement in a rat mesenteric arterial ring. At the beginning of the acquisition, the PE concentration was continuously increased from 0 μM to 100 μM. Then the pump was stopped for ∼6 min before the PE concentration was continuously decreased from 100 μM to 0 μM. After ∼15 min in a 0 μM PE solution, the responsiveness of the ring was checked with 100 μM of PE.

Cyclic pressure variations

Fig. 6 shows time-course simulations in the vasomotion domain of the calcium and radius dynamics of an artery subject to cyclic pressure variations (Fig. 6, a and b) and to a constant pressure of 100 mmHg (Fig. 6, c and d). With the parameter values for p₀, Δp₀, and f chosen (Table 2), Fig. 6, a and b, mimics a situation where blood pressure oscillates between a diastolic value of 80 mmHg and a systolic value of 120 mmHg, at a frequency corresponding to 60 heart beats per minute. On Fig. 6 b, vessel radius variations resulting from the pressure oscillations can be seen, in agreement with experimental observations (26). The calcium dynamics is not changed significantly in SMCs subject to a constant pressure p₀ compared to SMCs experiencing sinusoidal pressure variations with the same mean pressure p₀ (compare Fig. 6, panels a and c)). Only if the pressure oscillation frequency is similar to the vasomotion frequency (which is not physiological), is the calcium dynamics affected by becoming more chaotic (data not shown).

Discussion of model hypotheses

In this study, we have only considered the calcium dynamics of a single SMC, representing the mean smooth muscle calcium concentration of the arterial wall. The corresponding calcium dynamics in large populations of SMCs has been analyzed in our previous articles (18,25,27). Moreover, we have not taken into account the endothelium, as in our model the endothelium plays only a modulatory role. We have previously studied its precise effects (25,28).

We have assumed that the only effect of stress is to activate SACs without considering other possible mechanosensitive pathways. It has, for example, also been suggested that stress may activate the calcium release from the intracellular stores (29). This other possible pathway can be modeled by increasing the terms J_IP3 or J_CICR. This does not qualitatively change our results, as the cytosolic calcium concentration is then also increased and the three domains are shifted to the left (results not shown).

In our model, calcium and active force development are related by the cross-bridge phosphorylation model of Hai and Murphy (20). We have not introduced any cross-bridge velocity in this model (30), as the bifurcation diagrams represent the attractors (steady-state solution, periodical solution) to which the dynamical system converges after a certain time. The cross-bridge velocity does not intervene in the calculation of the steady-state solution (zero velocity), and the position of the oscillatory vasomotion domain coincides with the unstable part of the steady state. Within the oscillatory domain, the cross-bridge velocity can be neglected. Indeed, the oscillation frequency (ranging from 0.018 to 0.075 Hz (18)) is smaller than the smallest cross-bridge formation rate constants (Table 2), and therefore the spatial distribution of the cross-bridges AM and AMp approach the steady-state distribution at all times (30). The inclusion of the cross-bridge velocity is only important if one is interested in the time evolution of the dynamical system before it has converged to the attractors (31).

An in vivo condition has been mimicked by considering cyclic pressure variations, which is a considerable simplification. For instance, in vivo, different types of vasoconstrictors are released simultaneously, and this release often occurs in a pulsatile way (32). However, our aim here was to compare, in terms of wall stress, different experimental conditions. Note that Fig. 6, a and b, would be slightly changed if the cross-bridge velocity had been taken into account. Indeed, the high frequency arterial radius oscillations resulting from heartbeat would then decrease active force development (30). However, this effect is limited (30), as the amplitude of these radius oscillations is small (<2%). An analysis of this effect would need further investigations, and the inclusion of cross-bridge velocity would require a model based on partial differential equations (30,31).

The main conclusions (vasoconstrictor sensitivity, multistability) of our study are not qualitatively dependent on the precise model characteristics and parameter values. Indeed, the coexistence of multiple states under isometric conditions is only a consequence of the vessel presenting a myogenic response, and the enhanced vasoconstrictor sensitivity in isometric conditions results from a higher arterial wall stress. Our model results are in agreement with experimental findings in the literature. The multistability that may manifest itself by different concentration-response curves depending whether the vasoconstrictor concentration is increased or decreased has been verified experimentally in this study, as we have not found any experimental confirmation of this important model prediction in the literature.

CONCLUSION

We have compared bifurcation diagrams of the smooth muscle mean calcium concentration and of the arterial radius in isometric, isobaric, and isotonic conditions, and we have analyzed the effects of cyclic pressure variations. Having in mind that we have neglected the cross-bridge velocity during the cyclic pressure variations, we have shown that isobaric conditions seem the most realistic, as the calcium dynamics is similar under cyclic pressure variations (in vivo-like situation) and under a constant pressure (isobaric situation). The contraction is less pronounced in isotonic than in isobaric conditions, in agreement with experimental findings. Isometric conditions may considerably change the calcium dynamics. The sensitivity to vasoconstrictor of SMCs is higher in isometric than isobaric or isotonic conditions, in agreement with experimental observations. The threshold vasoconstrictor concentration necessary for vasomotion is therefore higher in isobaric than isometric setups. The model predicts that isometric conditions may generate some artifacts, and care should be taken in the interpretation of experimental results. Indeed, the model suggests that isometric conditions may generate the coexistence of multiple stable states. This prediction is independent of the precise model characteristics and parameter values and is only a consequence of the vessel presenting a myogenic response. The multistability may bring about the condition that an existing vasomotion domain is missed in a concentration-response curve to vasoconstrictor, and that this curve is different depending upon whether the vasoconstrictor concentration is increased or decreased.

APPENDIX A: DETAILS OF THE MATHEMATICAL MODEL

The various terms appearing in Eqs. 1–5 are described by the following expressions as presented previously (18,25,27). The calcium flux

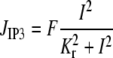(21)

models the calcium release from IP₃ sensitive stores,

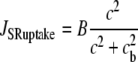(22)

models the SR/ER uptake,

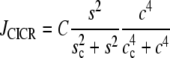(23)

describes the calcium-induced calcium release (CICR),

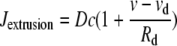(24)

is the calcium extrusion by Ca²⁺-ATPase pumps,

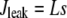(25)

corresponds to the leak from the SR,

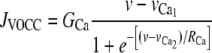(26)

is the calcium influx through VOCCs, and

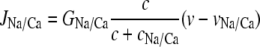(27)

is the Na⁺/Ca²⁺ exchange. The term

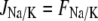(28)

is the Na⁺-K⁺-ATPase,

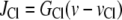(29)

models the chloride channels,

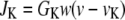(30)

is the K⁺ efflux,

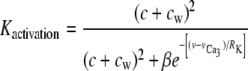(31)

describes the calcium and voltage activation of K⁺ channels, and the IP₃ flux

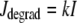(32)

models the IP₃ degradation. The constant 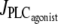is the rate of PLC activated by agonists. The parameter values for the SMC model are given in Table 1.