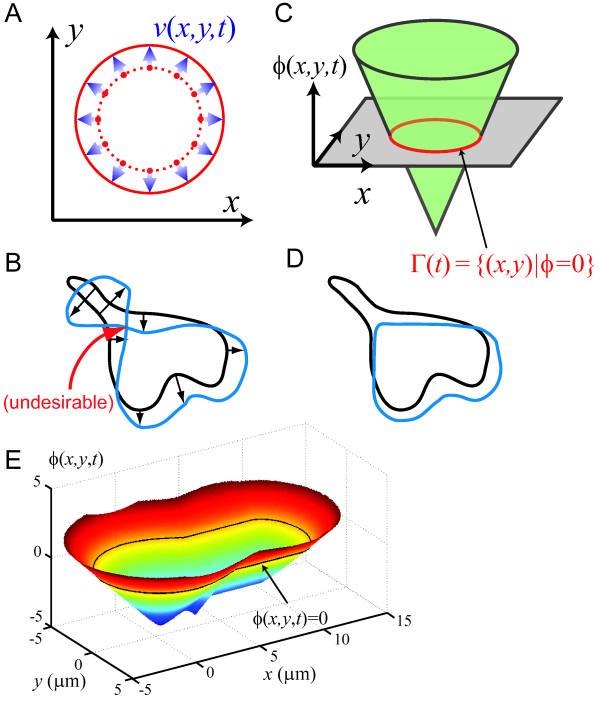
Figure 1.

Introduction to level set methods. A. The traditional method of tracking moving boundaries involves discretization of the boundary (dotted red) into a set of points, moving each point x = (x, y) according to the local velocity (v(x, t)), leading to a new boundary at the new locations (solid red). B. Difficulties can arise, however, when the geometry of the boundary becomes irregular. In this case, the point tracking method often fails to preserve the boundary topology. Special attention is required to resolve these errors, increasing computational costs. C. In the Level Set Method (LSM), the boundary Γ(t) is embedded into a higher dimensional potential function (ϕ(x, t)) as the zero-contour. Γ(t)moves as ϕ(x, t)evolves in time. D. Because the boundary is defined implicitly, the LSM framework overcomes some of the difficulties of boundary point tracking. E. This example illustrates how an arbitrary cell shape (black contour) can be embedded into a signed distance function to form the level set potential function ϕ(x, t). In this case, the potential function is given by the Euclidean distance to the cell boundary, with positive (resp. negative) sign when outside (resp. inside) the cell.