Survival of the Currently Fittest: Genetics of Rainbow Trout Survival Across Time and Space

Abstract

As a fitness trait, survival is assumed to exhibit low heritability due to strong selection eroding genetic variation and/or spatio-temporal variation in mortality agents reducing genetic and increasing residual variation. The latter phenomenon in particular may contribute to low heritability in multigeneration data, even if certain cohorts exhibit significant genetic variation. Analysis of survival data from 10 year classes of rainbow trout reared at three test stations showed that treating survival as a single trait across all generations resulted in low heritability (h² = 0.08–0.17). However, when heritabilities were estimated from homogeneous generation and test station-specific cohorts, a wide range of heritability values was revealed (h² = 0.04–0.71). Of 64 genetic correlations between different cohorts, 20 were positive, but 16 were significantly negative, confirming that genetic architecture of survival is not stable across generations and environments. These results reveal the existence of hidden genetic variation for survival and demonstrate that treating survival as one trait over several generations may not reveal its true genetic architecture. Negative genetic correlations between cohorts indicate that overall survival has limited potential to predict general resistance, and care should be taken when using it as selection criterion.

FITNESS traits such as survival and fecundity are commonly assumed to have low or close to zero heritability (Fisher 1930; Mousseau and Roff 1987; Roff and Mousseau 1987; Price and Schluter 1991; Merilä and Sheldon 1999; Coltman et al. 2005). Genetic analyses of survival have typically supported this assumption by finding little evidence of genetic variation from diverse taxonomic groups both in farmed (e.g., Van Arendonk et al. 1996; Knol et al. 2002; Goyache et al. 2003; Casellas et al. 2007) and in wild animals (e.g., Futuyma et al. 1995; Campbell 1997). However, in some instances moderate to high heritabilities for survival have also been found (e.g., Robison and Luempert 1984; Ernande et al. 2004; Kenway et al. 2006). Even with fairly low heritability of survival, animal breeding programs have produced slow but significant long-term genetic improvement in survival, contributing to increased animal welfare and economic profitability (Knol et al. 2002; Goyache et al. 2003).

The low heritability of survival is generally hypothesized to be a result of strong selection on this important fitness component, reducing additive genetic variance for survival (Fisher 1930; Mousseau and Roff 1987; Roff and Mousseau 1987). Additionally, it is not evident that multiple agents of mortality (e.g., different diseases, predators, physiological effects) share common genetic determination, thus possibly lowering survival heritability by reducing genetic variance and/or increasing residual variance (Price and Schluter 1991; Houle 1992; Hoffmann and Merilä 1999; Merilä and Sheldon 1999). The latter phenomenon in particular may occur when heritability of survival is estimated across large multigeneration data sets. Parents and offspring may experience different mortality factors that have clear heritable effects, resulting in moderate survival heritability within both cohorts. However, if the mortality factors do not share a common genetic basis, there will be a low parent–offspring regression that will contribute to a low heritability across the whole multigeneration data, even if there is heritable variation within both cohorts. This creates a situation where significant genetic variation existing within specific cohorts is hidden. This possibility, however, has remained unexplored.

For survival, an example of such hidden genetic variation could be a situation, where during certain years mortality is caused by a single major factor (e.g., a specific disease) for which there exists high genetic variation, while during other years, there may be multiple mortality factors and heritability is therefore low. It is well established that different environments affect heritability of traits (Hoffmann and Merilä 1999; Kause and Morin 2001; Charmantier and Garant 2005). Moreover, different cohorts (e.g., generations, herds, test stations) may experience different mortality factors that each display significant genetic variation, but the factors may be weakly or even negatively correlated with each other. Resistance to different mortality factors would then display genetic trade-offs (Gjøen et al. 1997; Cotter et al. 2004; Henryon et al. 2005; Luong and Polak 2007). In such a case, heritability from the whole combined data set may produce a zero-heritability estimate, even when cohort factors are correctly modeled in the statistical analysis.

To test for the existence of hidden genetic variation for survival, we analyzed extensive data on survival of rainbow trout (Oncorhynchus mykiss Walbaum) collected from 10 year classes of the Finnish national breeding program. The benefit of using rainbow trout to test our hypotheses is that due to the semiwild production environment, trout are exposed to natural variability in climate conditions, diseases, and parasites that create extensive spatial and generation-to-generation variability in mortality factors. Fish breeding programs also have discrete generations and distinct production environments. For instance, in addition to the abiotic environment differences, freshwater and sea have diseases that are specific to each environment. This differs from terrestrial farm animals that are often held under more standardized environmental conditions, and distinguishing separate generations and effects of different environments is more difficult. In wild animals, multigeneration pedigreed populations have only recently become available for genetic analysis (Quinn et al. 2006; Kruuk and Hill 2008) but recording of survival remains a challenge.

In this study, we first estimated heritability of survival in two environments across the whole data set, to find out whether or not the assumption of low heritability for overall survival is fulfilled. Second, to assess whether or not the genetic architecture of survival remains stable through space and time, the whole data were split into separate generations and three test stations, and cohort-specific heritabilities as well as genetic correlations between survival in different cohorts were estimated.

METHODS

The data originated from the Finnish national rainbow trout breeding program maintained by the Finnish Game and Fisheries Research Institute and MTT Agrifood Research Finland at the Tervo freshwater nucleus station in Central Finland (Kause et al. 2005).

Population structure:

The data included 121,905 individuals with observations originating from 10 year classes from 1995 to 2004 reared at one to three test stations located either in freshwater or in the sea (Table 1). A total of 1159 ancestors without observations and fertilized in 1989, 1990, 1992, and 1993 were included to complete the pedigree. The fish belonged to three subpopulations (PopI, PopIIa, and PopIIb; Table 1) with three to four successive generations. Each year class consisted of 109–341 full-sib families generated from 48–168 sires and 79–252 dams, mated using either nested paternal or partial factorial designs. The total numbers of fish within each year class were 4459–13,643 in the freshwater station and 1456–5165 in the sea stations (Tables 1 and 2). All populations share a common base population from which parents were sampled in 1989 for PopI and in 1990 for PopIIa and PopIIb. PopIIa and PopIIb diverged after one generation, with generations in 1996 and 1997 sharing six sires and 23 dams born in 1993. Population structure is detailed in Table 1.

TABLE 1.

Population structure and mating designs

Population/generation	Fertilization year	Sires	Dams	Mean (range) dams per sire	Mean (range) sires per dam	Full-sib families	Family tanks	Sea test stations
Population I
1	1995	92	272	3.0 (1–5)	1.0 (1–1)	272	370	—
2	1998	71	128	1.8 (1–4)	1.0 (1–1)	128	132	—
3	2001	121	154	2.5 (1–6)	2.0 (1–3)	303	303	2
4	2004	130	93	1.9 (1–5)	2.7 (1–4)	250	250	2
Population IIa
1	1996	75	150	2.0 (1–4)	1.0 (1–1)	150	150	—
2	1999	48	109	2.3 (1–4)	1.0 (1–1)	109	150	2
3	2002	113	139	2.5 (1–6)	2.1 (1–3)	287	287	1
Population IIb
1	1997	65	79	2.9 (1–5)	2.4 (1–3)	191	228	—
2	2000	98	122	2.0 (1–5)	1.6 (1–3)	200	200	2
3	2003	168	155	2.0 (1–5)	2.2 (1–3)	341	341	2

TABLE 2.

Trait abbreviations, sample sizes, heritabilities (h²), common environment effects (c²) and their standard errors (SE), genetic (V_G) and phenotypic (V_P) variances estimated across the whole freshwater or sea data (OverallF and OverallS, respectively) and in cohort-specific split data (G95T-G03B)

Population/fertilization year	Locationa	Trait	Sample size	Survival (%)	c2 ± SE	h2 ± SE	VG	VP
All	F	OverallF	81499	72	0.05 ± 0.00	0.17 ± 0.02	0.0258	0.1975
All	Sa + Sb	OverallS	40405	71	0.04 ± 0.00	0.08 ± 0.02	0.0156	0.1934
PopI
1995	F	G95F	13643	80	0.04 ± 0.01	0.22 ± 0.05	0.0176	0.1634
1998	F	G98F	6096	74	0.03 ± 0.02	0.37 ± 0.11	0.0399	0.1962
2001	F	G01F	8399	50	0.02 ± 0.01	0.19 ± 0.04	0.0296	0.2504
2001	Sa	G01Sa	3929	58	0.00 ± 0.01	0.10 ± 0.03	0.0147	0.2451
2001	Sb	G01Sb	3948	54	0.03 ± 0.01	0.12 ± 0.05	0.0190	0.2495
2004	F	G04F	7501	71	0.00 ± 0.01	0.10 ± 0.03	0.0115	0.2076
2004	Sa	G04Sa	3748	79	0.01 ± 0.01	0.07 ± 0.04	0.0059	0.1662
2004	Sb	G04Sb	3745	88	0.02 ± 0.01	0.04 ± 0.05	0.0017	0.1050
PopIIa
1996	F	G96F	7480	78	0.01 ± 0.01	0.20 ± 0.06	0.0172	0.1712
1999	F	G99F	4459	74	0.00 ± 0.01	0.71 ± 0.11	0.0819	0.2121
1999	Sa	G99Sa	1863	68	0.01 ± 0.02	0.68 ± 0.13	0.0980	0.2463
1999	Sb	G99Sb	1770	71	0.04 ± 0.02	0.32 ± 0.10	0.0395	0.2184
2002	F	G02F	5503	65	0.06 ± 0.02	0.24 ± 0.07	0.0331	0.2280
2002	Sa	G02Sa	1456	60	0.00 ± 0.02	0.27 ± 0.10	0.0414	0.2447
PopIIb
1997	F	G97F	10262	73	0.04 ± 0.01	0.18 ± 0.05	0.0172	0.1683
2000	F	G00F	7916	77	0.04 ± 0.01	0.38 ± 0.08	0.0378	0.1901
2000	Sa	G00Sa	4932	80	0.04 ± 0.01	0.34 ± 0.08	0.0268	0.1642
2000	Sb	G00Sb	4798	75	0.01 ± 0.01	0.45 ± 0.08	0.0479	0.1983
2003	F	G03F	10240	71	0.03 ± 0.01	0.35 ± 0.05	0.0438	0.2178
2003	Sa	G03Sa	5051	56	0.02 ± 0.01	0.20 ± 0.05	0.0320	0.2509
2003	Sb	G03Sb	5165	84	0.05 ± 0.01	0.70 ± 0.11	0.0454	0.1453

Values significantly different from zero are in italics.

^aF, Tervo freshwater nucleus station; Sa, Sb, sea test stations.

Rearing procedures:

The parents for each generation were selected on the basis of their estimated breeding values for growth (since 1992), maturity age (2001), external appearance (2001), fillet color (2003), and cataract by Diplostomum parasite (2003) (Kause et al. 2005). Parental fish were mated at the Tervo freshwater nucleus station during April–June. Full-sib egg batches were incubated separately, and at the eyed-egg stage, each full-sib family was transferred to one or two indoor 150-liter family tanks (Table 1). Eggs hatched in July. During the winter after hatching, fingerlings were removed from the family tanks and individually tagged with passive integrated transponders (Trovan, Germany).

After tagging, the fish were transferred to an outdoor raceway at the freshwater station and/or sent to one or two Baltic Sea test stations (Table 1). At the freshwater station the fish were held in a flow-through earth-bottomed raceway. All sea stations were located in southwest Finland within a maximum distance of 163 km from each other, but they were not the same ones from generation to generation. At the sea stations, the fish were reared under commercial farming conditions in a net pen. All fish were fed commercial fish feed pellets throughout the rearing cycle. The rearing procedure is detailed by Kause et al. (2005).

Trait definitions:

The survival data were collected after the tagged fish had spent one growing season either at the freshwater or at the sea station. At the end of the growing season, all fish remaining were captured and their individual tags recorded. The fish that survived from tagging to the end of the growing season were scored as survived (= 0), while fish not present in the end were coded as missing (= 1).

To estimate heritability over all generations, a trait “overall survival” was defined as survival at the freshwater station (trait OverallF, Table 2) and survival at the sea stations (trait OverallS, Table 2) across all generations. To estimate cohort-specific genetic architecture, the data were next split into 21 separate survival traits, by defining survival in each generation and in each of the three test stations as separate traits (Table 2).

Genetic analysis:

Heritabilities and genetic correlations between cohorts for survival were estimated using restricted maximum-likelihood and multitrait animal models (DMU-AI software; Madsen and Jensen 2008).

The model for overall survival at the freshwater station was

(1)

and for overall survival at the sea stations was

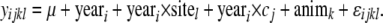(2)

The 21 generation- and test-stationwise traits were modeled as

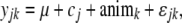(3)

where μ is a mean of a given trait, year_i is the fixed effect of fertilization year (i = 10 years), year_i × c_j is the random interaction effect of birth year with common environment effect shared by full sibs before tagging (j = number of family tanks), year_i × site_l is the fixed interaction effect of birth year and sea test station (l = 2 sites), anim_k is the random genetic animal effect (k = number of animals), and ɛ is a random error term. The common environment effect was modeled separately for each birth year because each tank does not have a consistent effect every year.

Both overall survival traits were analyzed simultaneously in a single two-trait analysis using models 1 and 2, respectively. These models estimate genetic (co)variation of the traits in the whole population because all animals originated from the same base population. Heritabilities and genetic correlations for generation- and test-stationwise analysis were derived from one multitrait model (using model 3) run performed separately for each population, resulting in eight, six, and seven trait runs for PopI, PopIIa, and PopIIb, respectively. Because within a population, all cohort- and generation-specific traits were included in a single multitrait run, the potential effect of selection bias on variance components should be reduced (Ouweltjes et al. 1988).

Heritability was quantified as h² = V_G(V_G + V_C + V_R)⁻¹, where V_G is genetic variation, V_C variation due to common environment, and V_R residual variation. Although genetic variance is assumed to be mainly due to additive genetic effects, the potential effects of dominance and epistasis cannot, however, be excluded. The common environment effect was quantified as c² = V_C(V_C + V_G + V_R)⁻¹. In addition to common environment effects of full sibs, V_C may potentially include parts of dominance variance. Asymptotic standard errors for genetic parameters were computed on the basis of a Taylor series approximation (Madsen and Jensen 2008).

Heritabilities estimated by the linear model were transformed to the underlying liability scale using the formula of Dempster and Lerner (1950). Genetic correlations of binary traits estimated using linear models are unbiased (Mäntysaari et al. 1991). Because only one survival trait was recorded from each individual, residual covariance was set to zero when calculating all the correlations. Moreover, when calculating genetic correlations across generations, covariance due to the common environment was set to zero.

Genetic covariance between survival in different generations was assessed in two ways. First, genetic correlations between generations were estimated. Second, for a subset of the cohorts, a correlation was calculated between the breeding values of parents estimated either from the observations of their own generation or from those of their offspring's generation only (Ødegård et al. 2007). The latter can be regarded as realized breeding values of the parents. A correlation between the two types of breeding values was calculated for the parental individuals contributing to the offspring generation (n = 144–364 parents in each generation). The model for estimating breeding values was the same as the above used for the split data (model 3).

Furthermore, to enhance the visualization of genetic correlation matrices, a principal component analysis was conducted (Rao 1964). The principal components for each population were calculated separately from their estimated full genetic correlation matrices. The analysis (PROC PRINCOMP) was conducted using SAS v. 9.1.3 (Sas 2005).

RESULTS

Overall survival—whole data:

As expected, heritability for overall survival across all generations and subpopulations was low (Table 2). In the sea, heritability was low but significantly different from zero (h² = 0.08 ± 0.02). At the freshwater station, heritability was 0.17 ± 0.02 (Table 2). Genetic correlation between freshwater and sea was positive and significantly different from both zero and unity (r_G = 0.58, 95% confidence interval = 0.39–0.76), indicating moderate genotype–environment interaction.

Cohortwise survival—split data:

Heritabilities within cohorts:

When all generations and test stations were analyzed as separate traits, an extensive variability in the heritability values was revealed, the 21 individual heritabilities ranging from 0.04 to 0.71 (Table 2). The highest heritabilities were in the generations 1999, 2000, and 2003. The means of the individual heritabilities (0.29 and 0.30 at freshwater and sea stations, respectively) were higher than the heritabilities for overall survival.

Genetic correlations between generations:

Of the 46 genetic correlations across generations, 8 were significantly positive (range 0.39–0.89), 16 significantly negative (range −0.97– −0.45), and 22 did not differ from zero (range −0.54–0.54; Table 3). Similar to the variation in heritabilities, this suggests again that the genetic architecture of survival does vary between generations. In addition to being correlations across generations, some of these correlations are also between test stations in different generations.

TABLE 3.

Genetic correlations and their standard errors between generations and test stations in three subpopulations

	G95F	G98F	G01F	G01Sa	G01Sb	G04F	G04Sa
PopI
G98F	0.48 ± 0.27
G01F	0.21 ± 0.43	0.52 ± 0.19
G01Sa	−0.20 ± 0.56	0.02 ± 0.28	0.29 ± 0.16
G01Sb	−0.38 ± 0.68	0.24 ± 0.31	0.39 ± 0.17	0.90 ± 0.19
G04F	0.47 ± 0.90	0.22 ± 0.42	0.13 ± 0.24	0.73 ± 0.27	0.48 ± 0.32
G04Sa	−0.48 ± 1.04	0.13 ± 0.51	−0.15 ± 0.31	0.70 ± 0.36	0.82 ± 0.40	0.38 ± 0.24
G04Sb	−0.34 ± 1.36	−0.53 ± 0.72	−0.54 ± 0.47	0.19 ± 0.54	0.07 ± 0.58	0.17 ± 0.33	0.37 ± 0.46
	G96F	G99F	G99Sa	G99Sb	G02F
PopIIa
G99F	−0.83 ± 0.18
G99Sa	−0.72 ± 0.22	0.97 ± 0.04
G99Sb	−0.74 ± 0.28	0.95 ± 0.09	0.94 ± 0.11
G02F	0.54 ± 0.40	−0.45 ± 0.22	−0.40 ± 0.24	−0.41 ± 0.30
G02Sa	0.89 ± 0.41	−0.91 ± 0.18	−0.85 ± 0.24	−0.90 ± 0.32	0.71 ± 0.19
	G97F	G00F	G00Sa	G00Sb	G03F	G03Sa
PopIIb
G00F	0.49 ± 0.24
G00Sa	0.61 ± 0.24	0.93 ± 0.07
G00Sb	0.49 ± 0.23	0.89 ± 0.06	0.98 ± 0.05
G03F	−0.51 ± 0.30	−0.84 ± 0.11	−0.96 ± 0.11	−0.97 ± 0.08
G03Sa	−0.03 ± 0.36	−0.69 ± 0.17	−0.58 ± 0.20	−0.61 ± 0.17	0.68 ± 0.10
G03Sb	−0.20 ± 0.32	−0.75 ± 0.13	−0.86 ± 0.13	−0.93 ± 0.10	0.94 ± 0.05	0.73 ± 0.09

Trait definitions are in Table 2. Correlations significantly different from zero in are in italics (95% confidence intervals do not include zero).

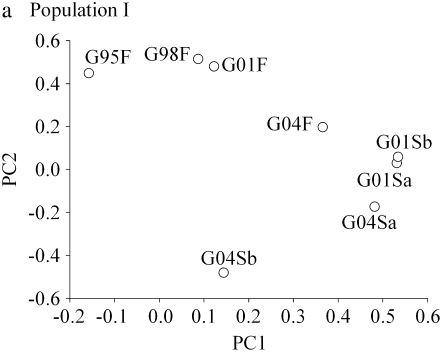
When the results are examined within each population, clear patterns emerge for the negative correlations (Table 3). In PopI, genetic correlations between generations at the freshwater station were positive (mean correlation = 0.34, range 0.13–0.52), whereas the negative correlations occurred only between the freshwater station and the sea stations (mean correlation between generations = −0.08, range −0.54–0.73). This result was also clearly visualized by the results of the principal component analysis on the full genetic correlation table for this population (Figure 1a). When the first two principal components were plotted, the freshwater traits were located in the top left-hand corner, whereas the seawater traits were located in the bottom right-hand corner. That two principal components were needed to clearly separate fresh- and seawater environments is logical because each of the two first principal components explained 30–40% of the variation (Table 4).

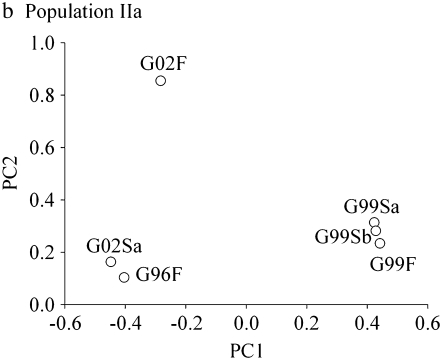
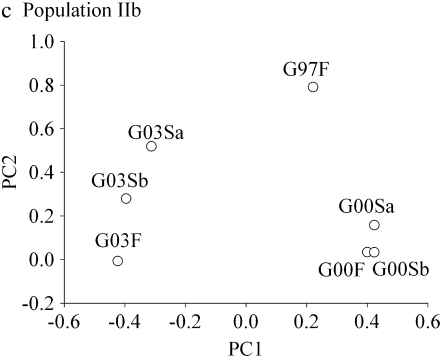
Figure 1.—

Individual survival traits plotted along the first and second principal component axes for each population. Trait abbreviations are given in Table 2.

TABLE 4.

Principal component analysis of the full genetic correlation matrices for the three populations

PC	Eigenvalue	Prop%	Cum%
PopI
1	3.22	40.3	40.3
2	2.47	30.9	71.2
3	1.29	16.1	87.3
4	0.68	8.6	95.9
PopIIa
1	4.82	80.3	80.3
2	0.80	13.3	93.6
3	0.29	4.9	98.5
4	0.08	1.3	99.8
PopIIb
1	5.37	76.7	76.7
2	1.08	15.4	92.1
3	0.36	5.1	97.2
4	0.19	2.7	99.9

For each of the first four principal components (PC), eigenvalues, proportion of variance explained (Prop%), and cumulative explanation percentage (Cum%) are given.

The patterns of both PopIIa and PopIIb differed from that of PopI, but do resemble each other. Both PopIIa and PopIIb were characterized by a single generation that is negatively correlated with the other generations. In PopIIa, the genetic correlations between 1996 and 2002 were positive [r_G (SE): G96F vs. G02F, 0.54 (0.40); G96F vs. G02Sa, 0.89 (0.41)], but these generations were negatively correlated with 1999 (mean genetic correlation = −0.69, range −0.91– −0.40; Table 3). The first principal component explained 80.3% of the variance (Table 4) and clearly separated generation 1999 from the two others (Figure 1b).

Similarly to the pattern found in PopIIa, in PopIIb the generation 2003 correlated negatively with generations 1997 and 2000 (mean correlation = −0.66, range −0.91– −0.40; Table 3) and the generations 1997 and 2000 were significantly positively correlated with each other (range 0.49–0.61; Table 3). Again most of the variation was explained by the first principal component (76.7%) and in the plot of the first and second principal components the generation 2003 formed its own cluster (Table 4, Figure 1c).

Correlations between breeding values calculated from parental and offspring generations:

In general, correlations of breeding values produced results similar to the genetic correlations between generations, revealing both significant negative and positive correlations (Table 5). Of 18 correlations for breeding values, 6 were significantly positive, 5 significantly negative, and 7 nonsignificantly different from zero.

TABLE 5.

Comparison of genetic correlations (r_G) with correlations between breeding values estimated from parental and offspring generation observations (r_S)

Parent trait	Offspring trait	rG	rS
PopI
G95F	G98F	0.48	0.04
G98F	G01F	0.52	0.44
G98F	G01Sa	0.02	0.17
G98F	G01Sb	0.24	0.34
G01F	G04F	0.13	0.08
G01F	G04Sa	−0.15	−0.08
G01F	G04Sb	−0.54	−0.13
PopIIa
G96F	G99F	−0.83	−0.25
G96F	G99Sa	−0.72	−0.19
G96F	G99Sb	−0.74	−0.13
G99F	G02F	−0.45	−0.39
G99F	G02Sa	−0.91	−0.24
PopIIb
G97F	G00F	0.49	0.14
G97F	G00Sa	0.61	0.36
G97F	G00Sb	0.49	−0.11
G00F	G03F	−0.84	0.07
G00F	G03Sa	−0.69	−0.05
G00F	G03Sb	−0.75	0.14

Trait definitions are in Table 2. r_G, genetic correlation between two cohorts; values with their standard errors are shown in Table 3. r_S, Spearman's correlation between breeding values estimated from parental generation observations in the freshwater station and their next generation progeny reared at three test stations. Values significantly different from zero are in italics.

In PopI and PopIIa, genetic correlations and correlations between breeding values were the same sign and produced similar patterns. For PopIIb, in two of six cases the genetic correlations were significantly negative but the correlations between breeding values were significantly positive (Table 5). Generally, the two methods produced similar results.

Genetic correlations between test stations within generations:

In general, genetic correlations between the test stations within generations were much more stable and more positive than those between generations (Table 3). Of the 16 genetic correlations calculated between the test stations within generations, 12 were significantly positive (range 0.39–0.98), of which 9 did not differ from unity. Four correlations were positive but not significantly different from zero (range 0.17–0.38; Table 3). In line with the analysis of overall survival across the whole data, these results substantiate that survival exhibits moderate genotype–environment interaction and that the genetic architecture of survival varies from test station to test station.

DISCUSSION

On the basis of our genetic analysis of multigeneration data from the pedigreed population of rainbow trout, we showed that genetic architecture of survival is not stable across generations and environments. Moreover, even negative genetic correlations can occur between survival in distinct cohorts. Spatio-temporal variation in genetic architecture for this closely related fitness trait resulted in low heritability for overall survival across the whole data set, hiding significant genetic variation in specific cohorts.

Revealing hidden genetic variation:

When survival in each of the two environments was regarded as a single trait across all generations, overall survival showed low heritability in both environments (freshwater h² = 0.17 ± 0.02, sea h² = 0.08 ± 0.02). While significantly different from zero, these heritability values are still in accordance with the hypothesis of low heritability for fitness-related traits (Fisher 1930; Mousseau and Roff 1987; Roff and Mousseau 1987; Price and Schluter 1991; Merilä and Sheldon 1999; Coltman et al. 2005). For instance, the review by Mousseau and Roff (1987) showed mean heritability of 0.26 for life-history traits assumed to be under strong selection and heritability of 0.46 for morphological traits assumed to be under weaker selection.

Our results confirm the assumption that the low heritability for overall survival may occur because there are different mortality factors in separate cohorts that do not share common genetic determination, thus blurring consistent differences between genotypes across cohorts. However, when our data were analyzed separately for each generation and test station, large variability in heritability values was revealed, the maximum heritability value being 0.71. Consequently, the genetic background of survival was not homogenous across the cohorts, and treating survival as one trait over several generations may hide its true genetic architecture. These statements are highlighted further by the fact that many of the genetic correlations across the generations were low or negative. By splitting the data into homogeneous cohorts, we were able to reveal genetic variation that would otherwise have been hidden. Similarly, in a study of selection response in the beginning of the Nile tilapia (Oreochromis niloticus) breeding program, Charo-Karisa et al. (2006) reported varying heritability of survival for the three generations (range 0.03–0.14). The reader should note that also the differences between the generations in mating ratios and population structure as well as sampling error may produce minor variation in the heritability estimates. However, these factors alone cannot explain the huge variability observed.

Furthermore, it is possible, yet speculative, that selection may have eroded genetic variation from overall survival, even if its component traits show high genetic variation. It is well established that separate components of survival, such as mortality against specific diseases or parasites, may display negative genetic correlations, facilitating the maintenance of genetic variation in the component traits (Gjøen et al. 1997; Cotter et al. 2004; Henryon et al. 2005; Leimu and Koricheva 2006; Ødegård et al. 2007).

Despite the well-justified logic that selection, genetic drift, and mutations modify genetic architecture of traits (Fisher 1930; Kimura 1958; Falconer 1960), early predictive evolutionary quantitative genetic models assumed that genetic architecture of traits remains unchanged (Lande 1979). However, several experimental approaches have since illustrated the way heritabilities and genetic correlations are modified in time and space. First, the impact of selection on genetic architecture has been assessed using artificial selection experiments (Shaw et al. 1995) and by comparing genetics of behavioral, morphological, and life-history traits assumed to be under different selection pressures (Gustafsson 1986; Mousseau and Roff 1987; Roff and Mousseau 1987; Kruuk et al. 2000). Second, the effects of mutation have been studied within laboratory populations (Houle et al. 1996; Camara and Pigliucci 1999). Third, comparative studies have examined the way genetic architecture has evolved at macroevolutionary timescales (Kause et al. 2001; Steppan et al. 2002). Fourth, genetic architecture has been shown to vary with environment quality (Kause and Morin 2001; Sgró and Hoffmann 2004; Charmantier and Garant 2005; Roff and Fairbairn 2007). Fifth, it has been shown that trait variation depends on its position in a trait hierarchy, where high-level life-history traits may accumulate genetic and/or environmental variation of the lower-level morphological and behavioral traits influencing them (Price and Schluter 1991; Houle 1992; Kause et al. 1999). Accordingly, currently the question is under which conditions, and why, does the genetic architecture evolve and vary (Steppan et al. 2002).

Our study is most closely related to the fourth and fifth categories. However, the originality of our study is that the variability of genetic characteristics of survival depends on trait expression, i.e., variation in factors causing mortality in the first place. Survival differs from conventional traits due to its complex origin. Especially crucial is that survival is influenced by underlying component traits whose expression may vary in time and space. Interestingly, it can be further envisioned that the magnitude of the genetic effect of a mortality factor may depend on the type and number of previous mortality factors. The correlation between them in particular will determine whether the new factor will magnify or cancel out the genetic variation induced by the previous factors. Although survival is defined and measured similarly throughout the study, it is a product of multiple (and mostly unknown) factors that may vary in their incidence between environments and generations. It is logical to assume that this phenomenon is also applicable to other traits with similar multicausal determination yet with a simple trait definition. Indeed, our findings of heterogeneity in genetic (co)variances across generations substantiate results by Kause et al. (2007), who found that the heritability of rainbow trout deformations is elevated only during the years when deformations are found in uncommonly high incidence and that these generations are negatively genetically correlated with other generations.

Is survival a measure of general resistance?

For animal breeders, a common goal is to select animals that have general resistance or robustness against multiple environmental disturbances, stressors, and mortality factors. This topic is currently becoming a major target of research because it strongly contributes to increased animal welfare and ability to manage animals across a wide range of environments (Mulder and Bijma 2005; Pertoldi et al. 2007). Likewise, in the wild, robustness influences the fitness of individuals, making understanding of robustness genetics and its developmental mechanisms of importance for evolutionary biology (Félix and Wagner 2008). With the advent of advanced molecular tools (Schwartz et al. 2007), it is now possible to assess and monitor genetic parameters of survival and other previously logistically unfeasible traits also in wild animal populations.

When survival data are collected over a large number of generations, overall survival is a potential easy measure of general resistance, given that genetic correlations between different cohorts are positive. In our analysis, many of the genetic correlations between generations and test stations were positive, but some specific cohorts displayed strong negative genetic correlations with the other cohorts. The negative correlations occurred systematically with certain generations (1999 and 2003 in PopIIa and PopIIb, respectively) or between freshwater and sea stations (PopI). Negative genetic correlations are genetic trade-offs, where the genetic background increasing survival in the presence of certain mortality factor(s) may reduce survival in the presence of another factor(s). Genetic trade-offs between resistance to different diseases have indeed been found in rainbow trout (Henryon et al. 2005) and Atlantic salmon (Gjøen et al. 1997).

These results imply that overall survival is not a perfect measure of general resistance, and care should be taken when using it as a selection criterion. In the worst-case scenario, resistance to a single factor may be reduced when selection is based on overall survival or survival in a single abnormal year. This may even lead to maladaptations in certain environments. An example of general resistance is presented in the meta-analysis by Leimu and Koricheva (2006), who found that genetic correlations between plant resistance to multiple natural enemies were mainly positive. Similarly, inbred lines or clones of aphids (Ferrari et al. 2001) and Daphnia (Decaestecker et al. 2003) have been shown to be resistant to several parasite, parasitoid, or pathogen species. In humans it has been suggested that some genotypes are less susceptible to multiple disorders (Rzhetsky et al. 2007).

The genetic correlations between freshwater and sea environments were positive in the overall analysis as well as in the cohortwise analyses. This suggests that to some extent the same genetic architecture is responsible for survival in different environments, in which different mortality factors may prevail. In contrast to the between-generation correlations, within generations there were no negative genetic correlations between the test stations. This may be understandable because within a generation, all paternal and maternal families experience similar initial conditions, including initial growth and potential diseases, which is likely to make correlations between environments positive rather than negative within a generation. For example, if the main mortality factor during a certain year is an infectious disease that has already attacked the fish during fingerling growth, family differences against this disease will create positive genetic correlations across all the test stations when mortality occurs during grow-out period. Such shared initial events do not influence genetic correlations calculated across generations.

In this study, principal components were used to visualize the patterns of the large correlation tables. As suggested by a reviewer, also direct estimates of genetic principal components could have been estimated from the raw data (Kirkpatrick and Meyer 2004; Meyer and Kirkpatrick 2005; Hine and Blows 2006). Using this approach, it is possible to identify the number of underlying latent variables and their genetic variation, generating the observed multiple genetic correlations (e.g., Blows et al. 2004; Mezey and Houle 2005). This would provide an additional vigorous way to quantify the degree of genetic variation for general resistance and robustness.

In conclusion, the results have two important implications. First, survival, a low-heritability trait closely related to fitness, displayed both zero and very high heritabilities when the data were split to more homogeneous cohorts. This implies that spatio-temporal variation may hide the underlying genetic architecture of overall survival. Second, overall survival across generations did not accurately measure general resistance or robustness, because some specific generations displayed strong negative genetic correlations with the other cohorts. Our study highlights the unique genetic characteristics that survival can have.