Renal blood flow and dynamic autoregulation in conscious mice

Abstract

Autoregulation of renal blood flow (RBF) occurs via myogenic and tubuloglomerular feedback (TGF) mechanisms that are engaged by pressure changes within preglomerular arteries and by tubular flow and content, respectively. Our understanding of autoregulatory function in the kidney largely stems from experiments in anesthetized animals where renal perfusion pressure is precisely controlled. However, normally occurring variations in blood pressure are sufficient to engage both myogenic and TGF mechanisms, making the assessment of autoregulatory function in conscious animals of significant value. To our knowledge, no studies have evaluated the dynamics of RBF in conscious mice. Therefore, we used spectral analysis of blood pressure and RBF and identified dynamic operational characteristics of the myogenic and TGF mechanisms in conscious, freely moving mice instrumented with ultrasound flow probes and arterial catheters. The myogenic response generates a distinct resonance peak in transfer gain at 0.31 ± 0.01 Hz. Myogenic-dependent attenuation of RBF oscillations, indicative of active autoregulation, is apparent as a trough in gain below 0.3 Hz (−6.5 ± 1.3 dB) and a strong positive phase peak (93 ± 9 deg), which are abolished by amlodipine infusion. Operation of TGF produces a local maximum in gain at 0.05 ± 0.01 Hz and a positive phase peak (62.3 ± 12.3 deg), both of which are eliminated by infusion of furosemide. Administration of amlodipine eliminated both myogenic and TGF signature peaks, whereas furosemide shifted the myogenic phase peak to a slower operational frequency. These data indicate that myogenic and TGF dynamics may be used to investigate the effectiveness of renal autoregulatory mechanisms in conscious mice.

blood flow to the kidneys is maintained constant when blood pressure (BP) fluctuates. This process, termed autoregulation, is achieved by active mechanisms and is essential for the maintenance of body salt and fluid homeostasis and for the protection of the glomeruli from pressure-induced injury (30). Active stabilization of renal blood flow (RBF) (and therefore glomerular filtration rate, GFR) is largely controlled by regulation of preglomerular vascular resistance through changes in the diameter of the afferent arterioles and to a lesser extent the interlobular arteries (16, 44). Two major mechanisms mediate autoregulation of RBF, the myogenic response and tubuloglomerular feedback (TGF). The myogenic mechanism is an intrinsic property of the vascular smooth muscle to contract in response to increases in pressure and to relax in response to decreases in arterial pressure (9, 18, 19). TGF regulates preglomerular vascular resistance in response to changes in distal tubular fluid composition and flow (8, 9, 18, 19, 30). Together these mechanisms work in concert (8) to maintain a constant RBF and GFR across a range of renal perfusion pressures (39).

The general principle governing studies designed to assess autoregulation of RBF involves measurement of RBF in response to changes in renal perfusion pressure (9, 26). The characteristics of the input signal (change in renal perfusion pressure) varies with experimental design and dictates the type of information that can be obtained. Frequently, changes in renal perfusion pressure are imposed externally and require extensive instrumentation of the anesthetized animal. When pressure changes are imposed in a “ladder” fashion, allowing pressure and flow to reach equilibrium between steps, only steady-state responses of the overall autoregulatory machinery are assessed (2). When information about the interaction between the myogenic response and TGF and their respective contribution to renal autoregulation is of interest, pressure “ramps” or single steps are imposed, and the kinetic properties of autoregulatory mechanisms can be assessed (49). However, these studies are largely performed in the anesthetized animals, including mice (15, 27). In conscious, freely moving animals, BP varies continuously (24, 38). Such spontaneous BP fluctuations are sufficient to engage renal autoregulatory mechanisms; therefore, methods designed to assess RBF autoregulation under dynamic conditions have been successfully used in experimental animals in the conscious state, but not in mice (9, 19, 48).

Studies using chronically implanted RBF probes and arterial catheters for direct and simultaneous measurements of RBF and arterial pressure in conscious animals can provide useful data to describe oscillatory phenomena that occur in both pressure and flow (2, 14, 48). Periodic components of either BP or RBF signals appear as discrete peaks in the power spectrum (9, 45). Bearing on the aforementioned principle that changes in RBF in response to variations in pressure may be used to describe autoregulation, one can consider spontaneous oscillations in BP as the input and the corresponding oscillations in flow as the output of a transfer function that describes the operation of autoregulatory mechanisms (9). One major advantage of this approach is that physiological variations of BP are used, and the animals are conscious and freely moving. The other major advantage of this technique is that it allows investigation of the dynamic properties of the autoregulation, which can provide information about the mechanisms involved (9, 18, 19).

Studies of RBF dynamics in rats (2, 8, 9, 13, 14, 42) or larger mammals (dogs) (48) with normal or hydronephrotic (16) kidneys, as well as in vitro studies of isolated kidneys (29), isolated perfused juxtamedullary preparations (47), or afferent arterioles (25) have consistently shown that the two autoregulatory mechanisms have distinct dynamic properties, with a faster myogenic response and a slower TGF. The response time of the myogenic mechanism is generally <10 s, whereas TGF takes a minimum of 30 s to completion (26). These differences are due to longer lags in the sensing and transduction of the variable detected by TGF compared with the myogenic mechanism (tubular flow vs. transmural pressure, respectively) (9). Operation of the TGF also generates sustained oscillations in tubular pressure under free-flow or stop-flow conditions (28). When power spectra and transfer function between BP and RBF are assessed, these differences in dynamics result in characteristic “signatures” that allow identification of the operating characteristics of either myogenic or TGF mechanisms, in terms of rate, efficiency, interaction, and contribution to overall autoregulation (2, 9, 14, 20).

Although this methodology has been applied to animals ranging from dogs to rats (9, 26, 39), to date, there have been no studies evaluating RBF or RBF autoregulation in conscious freely moving mice. Given the current wealth of genetic models available, development of such a methodology to assess renal autoregulation in mice could be highly significant and very useful. In this study, we describe a method to measure RBF and assess dynamic autoregulation in conscious chronically instrumented mice. We combined spectral analysis of BP and RBF with pharmacological inhibition of myogenic and/or TGF mechanisms with the purpose of confirming the specificity of the dynamic parameters identified. To our knowledge, this is the first ever report of measuring RBF and/or using spectral analysis to evaluate RBF autoregulation in conscious mice.

METHODS

Animal preparation.

Adult (>30 wk of age) female inbred New Zealand White mice (NZW/LacJ; Jackson Laboratories, Bar Harbor, ME) were used for this study. Mice were placed in an induction chamber containing isoflurane anesthesia and thereafter maintained on isoflurane (1.5–2% in oxygen, delivered through a mask) for the duration of the surgery. Submandibular and dorsal hair was shaved with an electric shaver followed by the application of depilatory lotion to remove any residual hair. The surgical sites were prepared with a 70% ethanol solution. Body temperature of the mouse was maintained at 37°C throughout the procedure using a heating pad.

Arterial and venous catheters.

A carotid artery catheter was placed in the left common carotid to monitor mean arterial pressure directly as previously described (41). Catheters were heated and stretched to create an even taper with Renapulse (Braintree Scientific, Braintree, MA) tubing. A 1-cm segment of the catheter was inserted in the artery. Venous catheters implanted in the right jugular vein were made with microrenathane (MRE040; Braintree Scientific) that was slightly tapered by heat. The venous catheter was advanced ∼2 cm in the vein. Once in place, ligatures were tied around the catheter to hold it in place. A drop of 3M Vetbond (St. Paul, MN) was added to the insertion site to further anchor the catheter and prevent blood seepage.

Both catheters were tunneled subcutaneously to the nape of the neck and exteriorized through an incision located between the scapulas. Polyethylene Intramedic tubing (PE-240; Fisher Scientific) was cut to a 1.5-cm length and flanged at one end with heat. Both arterial and venous catheters were passed through the tubing, and the flange was sutured in place with 6-0 silk. The submandibular incision through which the placement of the catheters occurred was sutured with 6-0 silk suture.

Chronic RBF probe.

An ∼1-cm incision was made through the skin and muscle dorsal to the right kidney. Retractors (model no. 17003-03; Fine Science Tools, Foster City, CA) were used to separate the tissue and expose the kidney. Cotton-tipped applicators (model no. 14-960-3P; Fisher Scientific) were used to blunt dissect the connective and adipose tissue to clearly expose the renal artery and vein. When approaching from this side, the renal artery is positioned on top of the renal vein. The connective tissue between the artery and vein was completely or near completely removed using the cotton swabs. Use of this method dramatically reduced the potential to puncture the fragile renal vein and usually allowed sufficient dissection to position the perivascular flow probe. If difficulties arose in completely clearing the connective tissue between the artery and vein, a no. 5 forceps with a 45-degree angle (Fine Science Tools) was placed carefully between the two vessels and then gently opened to complete the dissection.

In preparation for placement of the flow probe, a subcutaneous “tunnel” was created between the renal incision site and the nape of the neck where the catheters were externalized. The chronic flow probe (0.5PSB; Transonic Systems, Ithaca, NY) consists of the probe head and a four-pin connector located at opposite ends of a 4-cm cable. The four-pin connector was passed subcutaneously to the nape of the neck at which time it was pressure fitted through a disposable skin button (model no. AAPL103; Transonic Systems). The connector was attached to the flowmeter via an extension cable to monitor flow during the procedure. The probe head was then positioned around the renal artery with attention paid to avoid kinking the vessel. Once a stable flow was achieved, the cable connecting the probe head and four-pin connector was sutured in place by passing 6-0 silk through the muscle wall and around the cable. Next, the retractors were removed, and Surgilube (E. Fougera, Melville, NY) was topically applied around the probe head to act as a coupling gel for the ultrasound signal. A 0.5-cm² section of Mersilene Mesh (Ethicon, Somerville, NJ) was used to wrap the probe head. Once completed, Kwik-Sil (World Precision Instruments, Sarasota, FL) elastomer was used to fill in around the mesh and probe head. Once the elastomer was set, 6-0 silk was used to suture the muscle and skin layers.

The final step was to secure the skin button in place between the scapulas. This was done by suturing the skin to the button using 4-0 silk via the four premade holes in the skin button. We attach the skin button at four additional points (passing the needle directly through the skin button) and have found that this greatly enhances the long-term stability of the skin button. Subcutaneous administration of carprofen (5 mg/kg) was given for postoperative analgesia.

Experimental protocol.

Animals were given 24 h to recover from the surgery. The four-pin connector was attached to the flowmeter cable, the signal of which was passed through a bridge amplifier and a Power Lab (ADInstruments, Colorado Springs, CO) to view and record the signal using a computerized chart recorder (Chart v5.5.3; ADInstruments). The arterial catheter was connected to a fluid-filled pressure transducer (Deltran II; Utah Medical Products, Midvale, UT) for continuous monitoring of arterial pressure. Both arterial pressure and RBF were sampled at a rate of 1,000 cycles/s for a minimum of 60 min to obtain basal pressure and flow. After baseline data were recorded, a bolus intravenous infusion of either the calcium channel blocker amlodipine (3 mg/kg) or the NaK2Cl cotransporter antagonist furosemide (1 mg/kg) was administered via the jugular vein catheter. These concentrations are within the ranges described to cause renal vasodilation (23) and inhibit TGF mechanism (37) in rats. BP and RBF were monitored for at least 30 min following the infusion.

Measurement of dynamic autoregulation.

Data analysis was performed using an automated Matlab (R12; Mathworks, Natick, MA) routine. The continuous BP signal was approximated using the Fast Fourier Transform as a sum of sine waves. The RBF was processed in a similar manner, and the relationship between the fractional variations in each signal (input to output) was determined at each individual frequency. BP and RBF data were obtained at a sampling rate of 1,000 Hz. Time-series data were visually inspected, and stationary subsegments of 20–30 min in duration were selected from each data set and used for further analysis. The selection ensured that the signal was free of artifacts related to movement of the animal. The resulting series were resampled at 20 Hz. A low pass filter was used to eliminate aliasing at frequencies below 10 Hz. Power spectra for BP and RBF were calculated using Welch's averaged periodogram on segments of 2,048 data points, with 50% overlapping, using a Hanning window. These parameters allowed a frequency resolution of 0.009 Hz. The admittance function was calculated as the ratio of the cross spectrum of BP (BP) and RBF to the BP power spectrum. Coherence between the two signals was also calculated as well as the magnitude and phase angle of the admittance function. The fractional gain in admittance was obtained by normalizing the admittance gain by the conductance computed over the selected segments. The natural frequencies of myogenic and TGF mechanisms were determined from their characteristic behavior identifiable in fractional gain and phase angle, as previously described for conscious rats or dogs between 0.1–0.4 Hz (myogenic) and 0.025–0.1 Hz (TGF) (9). The frequencies of the myogenic and TGF mechanisms were confirmed by inhibition of vasoactivity (amlodipine) and specific blockade of the TGF mechanism (furosemide), which resulted in attenuation of the peaks in fractional gain and phase angle at the respective frequencies.

Statistical analysis.

Spectral densities of BP and RBF, fractional gain in admittance, phase angle, and coherence are plotted for frequencies up to 1 Hz, for clarity. Standard errors, as depicted by the vertical lines in Figs. 1–3, were calculated at each frequency from the spectra of individual animals. For statistical comparisons, the peak in fractional gain and the peak value of the phase angle corresponding to the operation of the myogenic mechanism were calculated from spectra of individual animals between frequencies of 0.1–0.4 Hz and averaged. Similarly, the local maximum in gain and the associated peak in phase angle generated by the TGF mechanism were calculated between frequencies of 0.025–0.1 Hz and averaged. When no peaks were identified, these calculations were not performed (Table 1). Also, the maximal reduction in gain at frequencies below the myogenic resonance frequency (found at ∼0.31 Hz in normal mice) was calculated. To characterize the presence of 1/f pattern in BP and RBF, we calculated the β-coefficient as the slope of the linear regression of the logarithm of power density of BP and RBF on the logarithm of frequency up to 1 Hz. A value of β between 0.5 and 1.5 is considered to reflect a 1/f process (33). Statistical comparisons between groups were performed by one-way analysis of variance followed by the Newman-Keul's post hoc test for multiple comparisons, and values were considered statistically different at P < 0.05.

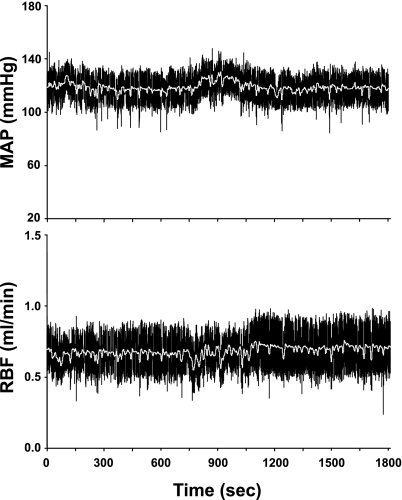
Fig. 1.

Example of raw blood pressure and renal blood flow data collected at 1,000 Hz in a conscious mouse.

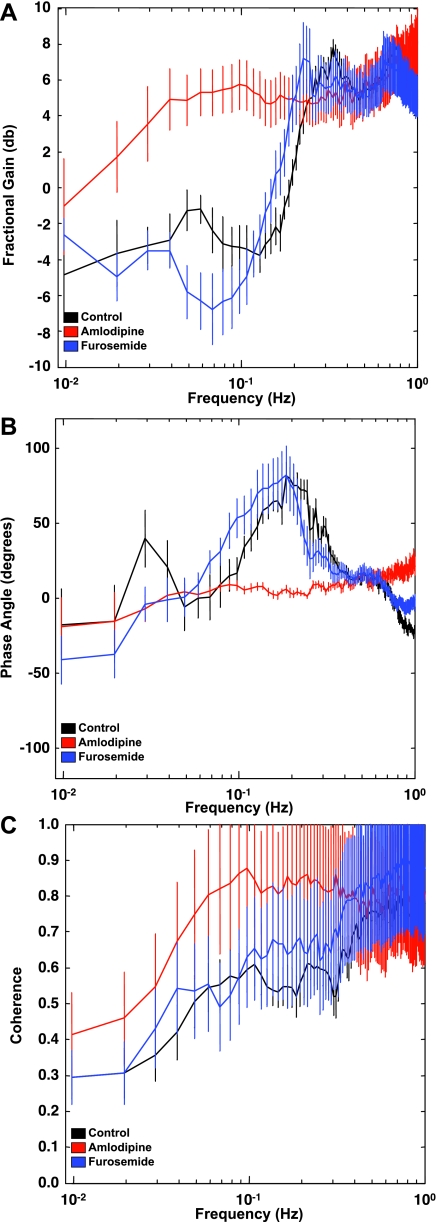
Fig. 3.

A: fractional gain in conscious mice under control conditions or after a bolus iv infusion of amlodipine or furosemide. B: phase angle in conscious mice under control conditions or after a bolus iv infusion of amlodipine or furosemide. C: coherence between blood pressure and RBF signals in conscious mice under control conditions or after a bolus iv infusion of amlodipine or furosemide.

Table 1.

Summary data

	Control	Amlodipine	Furosemide
n	13	6	6
MAP, mmHg	110±4	77±3*†	113±6
RBF, ml/min	0.83±0.06	0.63±0.10	0.74±0.08
Myo peak, Hz	0.31±0.01	ND	0.27±0.03
TGF peak, Hz	0.05±0.01	ND	ND
Myo phase, degrees	93.4±9.12	15.31±1.48*†	90.21±9.34
TGF phase, degrees	62.3±12.31	13.10±2.66*†	55.29±8.45
Myo trough gain, dB	−6.54±1.32	4.14±1.18*†	−7.51±2.17

Data are means ± SE; n, no. of experiments. MAP, mean arterial pressure; RBF, renal blood flow; Myo, myogenic; TGF, tubuloglomerular feedback.

^*P < 0.05 vs. control.

^†P < 0.01 vs. furosemide. ND, not detectable.

RESULTS

Under basal conditions, mean arterial pressure in mice was 110 ± 4 mmHg (n = 13), and RBF was 0.83 ± 0.06 ml/min (n = 13, raw RBF not corrected for kidney weight). Conductance was 7.5 ± 0.4 μl·min⁻¹·mmHg⁻¹. A sample of a raw BP and RBF tracing is shown in Fig. 1. Acute infusion of furosemide to block the TGF mechanism did not significantly alter BP, RBF, or conductance (6.5 ± 0.6 μl·min⁻¹·mmHg⁻¹). In mice that were administered an acute infusion of amlodipine, BP was reduced. Although RBF tended to be lower after amlodipine, this did not reach a statistically significant difference. Calculated conductance for these animals was not different (7.9 ± 1.0 μl·min⁻¹·mmHg⁻¹) compared with controls. The BP and blood flow data are summarized in Table 1.

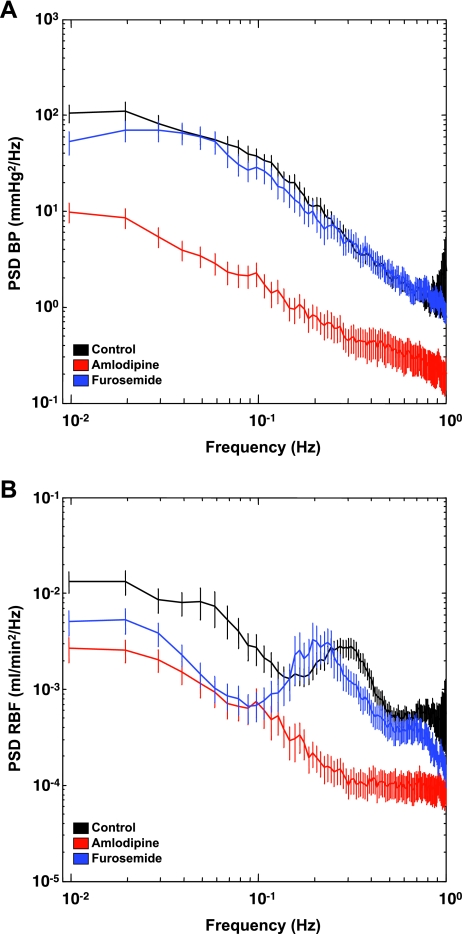
We used a Fast Fourier Transform of raw BP and RBF data to generate individual power spectra (Fig. 2, A and B). The black tracing represents basal conditions. Administration of amlodipine significantly reduced BP variability at frequencies below 1 Hz, whereas furosemide did not affect this parameter. The power spectrum for RBF displays a distinct peak at ∼0.3 Hz in the control animals (Fig. 2B). This peak was abolished by amlodipine but not furosemide. Spectral power of BP and RBF was higher at lower frequencies, consistent with the 1/f pattern previously described for most biological signals (33). The β-coefficient for BP was 1.34 ± 0.08 for control, 0.99 ± 0.1 for amlodipine, and 1.1 ± 0.05 for furosemide (P < 0.05, control vs. amlodipine). The β-coefficient for RBF was 0.86 ± 0.06 for control, 0.85 ± 0.10 for amlodipine, and 0.69 ± 0.09 for furosemide (P > 0.05).

Fig. 2.

Power spectral analysis of blood pressure (A) and renal blood flow (RBF; B) in conscious mice under control conditions or after a bolus iv infusion of amlodipine or furosemide. The RBF power spectrum shows a distinct peak in the frequency rage of 0.1–0.4 Hz that is abolished by amlodipine infusion. Black trace, basal conditions; red trace, amlodipine; blue trace, furosemide.

Fractional gain in admittance displayed two distinct peaks at 0.31 ± 0.01 Hz and at 0.05 ± 0.01 Hz in control animals. Also, there was a strong reduction in gain between 0.3 and 0.1 Hz (Fig. 3A), suggestive of active autoregulation generated by the faster myogenic mechanism. Amlodipine abolished both the peaks and the trough, and the gain displayed a monotonic decline toward 0 dB at the lowest frequencies resolved (Fig. 3A). This is indicative of passive transmission of pressure fluctuations in flow when active Ca²⁺-dependent vasoconstriction is blocked. The local maximum in gain at 0.05 Hz was abolished by acute infusion of furosemide (Fig. 3A), suggesting involvement of the TGF mechanism in the generation of this peak. In addition, a peak in gain was apparent at ∼0.7 Hz and was abolished by amlodipine but not furosemide infusion.

Figure 3B shows positive phase peaks at 0.21 ± 0.01 and 0.06 ± 0.01 Hz, corresponding with the sharp decrease in admittance gain and suggestive of the operation of myogenic and TGF mechanisms, respectively. Acute infusion of furosemide abolished the positive phase peak associated with TGF, whereas amlodipine infusion abolished both peaks, and phase angle remained close to zero across the frequency range. Infusion of furosemide also reduced the frequency at which the myogenic peak in phase occurred (0.21 ± 0.01 vs. 0.17 ± 0.01 Hz, P < 0.05, control vs. furosemide). A phase transition from positive to negative was apparent at 0.7 Hz, corresponding to the local maximum in gain, which was removed by amlodipine administration.

Coherence (Fig. 3C) is an index of the extent to which the pressure and flow signals are linearly related. Coherence values of at least 0.5 are required for reliable conclusions to be drawn from transfer function analysis, since linearity is an inherent assumption. The coherence between pressure and flow in our conscious mice is near one at frequencies >0.5 Hz (Fig. 3C). At frequencies <0.3 Hz, coherence declines but remains >0.5 until ∼0.05 Hz, when another decline becomes apparent.

DISCUSSION

In the present study, we outline an experimental protocol that demonstrates the feasibility of measuring RBF and mean arterial pressure in the conscious mouse. In addition, we demonstrate that assessment of dynamic RBF autoregulation can be achieved in mice using spectral analysis. To our knowledge, this is the first paper to report values of RBF in the conscious mouse and the first to perform analyses of dynamic autoregulation of RBF in the conscious mouse. Therefore, it is our hope that this study will be of use for investigators as they continue to take advantage of the wealth of genetic mouse models to examine the effect of specific genes on RBF autoregulation.

The use of spectral analysis to examine dynamic properties of complex physiological systems, including pressure and flow, is not a new technology. This method has been validated in larger rodent species such as rats and rabbits and in higher mammals such as dogs and recently reviewed by Cupples and Braam (9) and others (2, 18, 19, 26). The major advantage of this approach is that it allows assessment of the dynamic properties of renal autoregulation [changes in RBF (output) in response to spontaneous fluctuations in BP (input)] at multiple time points in conscious, unrestrained animals (2, 9). The data that are presented here for the first time in conscious mice are consistent with what has been reported in these other species. Importantly, we show that the operating frequencies of the myogenic and TGF peaks are similar in mice compared with rats, rabbits, and dogs (9, 26). The similar operating frequency for these regulatory mechanisms (along with pharmacological blockade by amlodipine and furosemide) helps to validate the utility of this approach in mice.

The transfer function analysis between BP and RBF allowed us to identify the dynamic operational characteristics of the renal autoregulatory mechanisms in the conscious mouse. A pattern of reduction in gain combined with a positive phase angle peak is consistent with the operation of an autoregulatory mechanism that acts to stabilize the output (RBF) in response to variations in input (BP) (9). The signature of the faster myogenic mechanism is apparent as a sharp reduction in gain together with a positive phase peak at frequencies below 0.3 Hz. These dynamic characteristics are similar to those previously described in conscious rats or dogs (9). The myogenic mechanism has been shown to generate feedback oscillations at its operating frequency. A peak in gain indicates amplification of RBF oscillations in response to pressure and suggests the presence of a resonance phenomenon (2, 9, 26). In our studies, a peak in admittance gain was also apparent at ∼0.3 Hz, indicative of myogenic-dependent resonance. The myogenic vasoconstrictor response requires intracellular Ca²⁺ entry (36). Blockade of L-type Ca²⁺ channels with dihydropiridines, such as amlodipine, abrogates this response in isolated arterioles in vitro (14). Moreover, chronic administration of Ca²⁺ channel blockers to the rat model of remnant kidney impairs renal autoregulation and promotes pressure-induced renal injury (14). We found that acute infusion of amlodipine abolished the reduction in gain and the corresponding peak in phase at frequencies between 0.1 and 0.3 Hz, consistent with inhibition of the myogenic mechanism.

Similar to many other species, the BP power spectrum in our study follows a 1/f pattern with no apparent peak, suggesting that no single mechanism dominates BP regulation in the conscious mouse (33). While 1/f noise is also apparent in the RBF spectrum, a unique characteristic of the RBF power spectrum from conscious mice is that an oscillation in RBF corresponding with the resonance peak of the myogenic response (∼0.3 Hz) is evident. Although feedback mechanisms operate with the same frequency in the afferent vasculature of different glomeruli, the oscillations they generate are not typically in phase, and no distinct oscillation appears in the total RBF (18, 19). There are two potential interpretations to the presence of this peak in the power spectrum of RBF in our study. First, the data can be interpreted to mean that the myogenic mechanism in preglomerular vasculature of nephrons in the mouse kidney operate in phase, thus generating a strong oscillation in total RBF, for reasons that are not clear. A similar oscillation in total RBF at the operating frequency of the myogenic mechanism becomes apparent in rats only under gas anesthesia (10). Previous studies of spontaneous oscillations in tubular pressure in rats found TGF-dependent synchronization in nephrons supplied by the same interlobular artery (17, 50). Recently, wavelet analysis applied to free-flow tubular pressure oscillations in normotensive rats indicated that synchronization arises not only for the TGF-induced oscillations but also for those induced by the operation of the myogenic mechanism (46). Our linear analysis techniques do not allow the detection of synchronization by conducted responses between subsets of nephrons. In any case, our results indicate that myogenic oscillations in individual nephrons, which occur within a narrow frequency range, may become apparent as a peak in the RBF spectrum. This may be due to the small number of nephrons in the mouse kidney [between 7,000 and 13,000 (7, 11, 21)]. On the other hand, it is possible that the peak in the RBF power spectrum represents an oscillation that is completely unrelated to a physiological regulatory mechanism. We believe that the latter is unlikely, however, given that this peak occurs at a similar frequency as the myogenic resonance peak apparent in admittance gain spectra. Moreover, the peak is abolished by treatment with amlodipine, but not furosemide. Therefore, we are confident that this represents the myogenic mechanism and that, in the mouse, the myogenic response is synchronous among individual vessel segments in the kidney.

We found that the operation of the TGF causes a local gain maximum at ∼0.05 Hz and a positive phase peak at frequencies below 0.05 Hz in the conscious mice. Similar patterns were found by investigators in larger species (9, 48). The local maximum in gain is thought to be generated by feedback oscillations induced by TGF at its operating frequency (19). Infusion of furosemide, known to block TGF (22, 43), abolished both the gain and the phase peaks, further confirming their TGF-related generation. Amlodipine also abolished dynamic signatures of TGF operation. This is expected since Ca²⁺ entry is required for TGF-induced changes in preglomerular conductance.

The signature of an autonomous oscillator was identified in the transfer function analysis, both as a distinct peak in gain and a sharp transition of phase angle from positive to negative. The operation of this oscillator was apparent at 0.7 Hz. Although other investigators observed this phenomenon in conscious rats, especially associated with hypertension (1, 9), its origin or functional significance remains elusive. Since we found that amlodipine infusion abolished both its gain peak and phase transition, we speculate that this oscillation is vascular in nature and requires Ca²⁺ entry for its manifestation.

Coherence between BP and RBF was higher than 0.5 at frequencies above 0.05 Hz, which validates transfer function analysis as performed in our study. Due to the complex interactions between autoregulatory mechanisms, analysis of frequency-dependent coherence may prove informative. We found that coherence was close to one at higher frequencies, whereas it declined sharply at ∼0.3 Hz and furthermore after 0.05 Hz, the operating frequencies of the myogenic and TGF mechanisms, respectively. Amlodipine treatment removed the stepwise decrease in coherence corresponding with the operating frequency of the myogenic response (0.3 Hz). The relative decrease in coherence at frequencies below 0.05 Hz is thought to reflect nonlinearity in the RBF dynamics, generated by the interaction of the two mechanisms (19).

This technique based on Fast Fourier transformations to investigate autoregulation of RBF has proven valuable and reliable in other animal models. In the present study we successfully used it for the identification of dynamic operational characteristics of the renal autoregulatory mechanisms in conscious mice. However, to perform such an analysis, there are important assumptions made and potential limitations to be considered. For example, at frequencies slower than 0.04 Hz (which should reflect the combined contribution of the myogenic and TGF mechanisms to overall autoregulation), the gain reaches a minimum of approximately −5 dB. This indicates an ∼55% autoregulation, which is lower than levels reported in steady-state experiments (∼90%) (1, 2, 14). One apparent explanation for such discrepancy is that steady-state techniques average out all dynamic components of the signals while dynamic approaches do not take into consideration the average values. Also, the lower estimate of autoregulation by linear dynamic techniques may be due to nonlinearities in the operation of either myogenic or TGF mechanisms, to the nonlinear interaction between them (19), or finally to the influence of nonautoregulatory influences on RBF (9), as reflected by the low coherence in that frequency band. Seminal studies from the laboratories of Marsh, Holstein-Rathlou, and Chon (3, 4, 31) have focused on the nonlinear dynamics of renal autoregulatory mechanisms and their interaction. Using nonlinear modeling with higher-order Volterra-Wiener kernels applied to BP-RBF data from rats, they demonstrated nonlinear properties of TGF as well as nonlinear crosstalk between the myogenic response and TGF. More advanced analytical techniques and mathematical models (34, 35), such as principal dynamic modes (32), stochastic recurrent neural networks for nonlinear autoregressive models (5), bispectrum (6, 40), double wavelet analysis (35), and the histogram of improved annealed competition of expert time frequency (12), are being applied to detect interactions between the two autoregulatory mechanisms. Whereas the physiological significance of the complex interactions between the two autoregulatory mechanisms remains elusive, we hope that the approaches delineated in the present study will provide the basis for even more comprehensive evaluation of the dynamics of renal autoregulation in mice amenable to genetic manipulation. In our study, using a linear approach, we were able to detect a significant impairment of autoregulatory efficiency following amlodipine administration (gain values >0 dB). Several investigators have suggested that the peaks in transfer gain resulting from resonance oscillations induced by the feedback mechanisms may be used as an indication of the strength of those mechanisms (1, 2, 14). While this assertion is still debatable, it is clear that the reduction in gain at frequencies below resonance (at least in the case of the myogenic mechanism) can be taken as a quantifiable parameter of myogenic autoregulation (9, 26, 39, 48). Indeed, we found that the trough in gain at frequencies immediately below the resonance frequency of the myogenic mechanism (<0.3 Hz) was completely abolished by amlodipine (gain became positive) but was not affected by furosemide. Experimental and modeling studies suggested frequency modulation of the myogenic response by the TGF, due to quadratic phase and frequency coupling between the two dynamic mechanisms (34, 40). In our study, during furosemide infusion, we were able to detect a reduction in the frequency at which the myogenic signature peak in phase occurred, which provides functional evidence that the myogenic mechanism may operate slower when TGF is blocked.

Taken together, we have demonstrated the feasibility of assessing dynamic autoregulation of RBF in the conscious mouse. This is the first study, to our knowledge, to adapt this methodology to mice. We propose that, in light of the large number of genetic mouse models available for study, spectral analysis of BP and RBF will prove to be a valuable tool for evaluating the effect of specific genes on myogenic and TGF mechanisms.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grant HL-085907 (M. J. Ryan) and American Heart Association National Scientist Development Grant 0830416N (R. Iliescu).