Abstract
Cells are dynamical systems of biomolecular interactions that process information from their environment to mount diverse yet specific responses. A key property of many self-organized systems is that of criticality: a state of a system in which, on average, perturbations are neither dampened nor amplified, but are propagated over long temporal or spatial scales. Criticality enables the coordination of complex macroscopic behaviors that strike an optimal balance between stability and adaptability. It has long been hypothesized that biological systems are critical. Here, we address this hypothesis experimentally for system-wide gene expression dynamics in the macrophage. To this end, we have developed a method, based on algorithmic information theory, to assess macrophage criticality, and we have validated the method on networks with known properties. Using global gene expression data from macrophages stimulated with a variety of Toll-like receptor agonists, we found that macrophage dynamics are indeed critical, providing the most compelling evidence to date for this general principle of dynamics in biological systems.
Keywords: complex systems, normalized compression distance, information theory
Many complex systems are capable of undergoing a phase transition between a disorganized and an organized state. This phenomenon has been observed in enzyme kinetics (1), growth of bacterial populations (2), foraging in ant colonies (3), brain activity (4), and traffic flow on the Internet (5). A system that is operating near such a phase transition is said to be critical. At equilibrium, this transition will occur at a critical value of a system parameter, such as the Curie temperature in a ferromagnet, below which the system can maintain spontaneous magnetization. Nonequilibrium systems, however, are capable of self-organizing to such a critical state, whereby complex behavior can emerge in a robust manner without fine-tuning the details of the system (6, 7).
A hallmark of critical behavior is the spontaneous emergence of complex and coordinated macroscopic behavior in the form of long-range spatial or temporal correlations. Such coordination across many scales enables information to propagate over time from one part of the system to another with a high degree of specificity and sensitivity. For example, measurements of human brain oscillations revealed such critical dynamics of neural networks, implying their ability to effectively propagate information and rapidly reorganize (8). Similarly, measurements of computer network traffic indicate that the Internet exhibits critical dynamics, accordingly, suggesting optimal information transfer (9, 10). Many other complex systems, such as financial markets (11), forest fires (12), neuronal networks supporting our senses (13), and biological macroevolution (14) have been shown to self-organize to a critical state.
A living cell is a complex dynamical system of interacting biomolecules. While this system exhibits stability even in varying environments, it is also capable of changing states and in so doing make decisions in response to specific changes in its environment, such as the initiation of cellular differentiation upon exposure to certain stimuli. Therein lies a delicate balance between stability and adaptability. Too much stability—a characteristic of ordered behavior—and the system cannot respond to changes, rendering it inflexible. Too much sensitivity—a feature of chaotic behavior—and the system loses its ability to maintain one or more stable steady states necessary for executing orderly cellular functions.
Such exquisite molecular decision-making is exemplified by the macrophage, a cornerstone cell type of the innate immune system and a key regulator of the inflammatory response. Batteries of cell surface receptors, such as the Toll-like receptors (TLRs), recognize different pathogen-associated molecular patterns and propagate that information through intracellular molecular networks (15). By combining the information associated with each of these molecular patterns, the macrophage triggers distinct (but overlapping) signal transduction pathways that lead to distinct gene expression programs (“bar codes”) corresponding to the specific invading microorganism. The macrophage uses this information to undergo a series of distinct functional state changes, resulting in cytoskeletal rearrangements, production of reactive oxygen and nitrogen intermediates, release of toxic peptides used to kill the pathogen, antigen presentation that activates specific T cells, and secretion of proinflammatory cytokines that further instruct the adaptive immune response. To carry out such complex and coordinated responses to the wide diversity of molecular patterns, the information read by the cell needs to flow through its molecular networks without being lost or degraded. The nature of this information flow constitutes the focus of our study.
It has long been hypothesized that living cells, as manifestations of their underlying networks of molecular interactions, are poised at the critical boundary between an organized and a disorganized state (16). Recently, several analytic approaches applied to gene expression datasets support the “life on the edge of chaos” hypothesis (17–19). If this hypothesis is true, criticality is a result of the cell's ability to coordinate complex behaviors while maintaining stability and robustness in a variable environment. More importantly, it represents a manifestation of a general principle governing the dynamics of living systems, placing them into a broader class of self-organized systems that are governed by the same universal principles. The equivalent principle in the study of the network architecture (i.e., structure) is the scale-free property (power-law degree distribution) shared by most real-world networks (20). Just as scale-free networks are extremely robust to random perturbations and are highly susceptible to specific targeted perturbations (attacks) (21), networks that are critical are also dynamically stable under most random perturbations, but undergo global state changes, such as macrophage activation, in response to targeted perturbations.
Quantifying Information Processing and Flow
Using an information-theoretic approach, we demonstrate that the macrophage exhibits dynamics in the critical regime at the boundary between order and chaos, providing the most compelling evidence to date for this general principle of dynamics in biological networks. Because sufficiently detailed quantitative descriptions of global system dynamics are not yet within reach (22), standard time-series analysis methods of detecting long-range (power-law) temporal correlations that are characteristic of critical systems (23) are not suitable for studying macrophage criticality. Instead, we approached the question of criticality from the perspective of information flow through a molecular network in the absence of a detailed description of the network itself. Recent studies have demonstrated that neglecting the details of biochemical interactions in favor of more coarse-grained statistical descriptions of large-scale dynamics can yield fundamental new insights into global regulatory information flow and signaling structure of complex molecular systems (24–26).
Consider two stimuli that transiently place the molecular system into two different states, where a state of a system at a given time is defined as the collective activity of its components, such as mRNA concentrations. If we can quantify the difference between the information content of these two states, we can then ask how this information difference changes as the system proceeds forward in time. Information loss can occur in two different ways. On the one hand, the successor states of the system may tend to be more similar than their predecessor states, leading to informational convergence. In contrast, the successor states may become more dissimilar, resulting in informational divergence. In the former case, the system forfeits discriminatory sensitivity in that it tends to “forget” the differences that distinguish different stimuli. In the latter case, robustness is killed because even small differences get amplified, making it difficult or impossible to reliably propagate information over time. In terms of information dynamics, critical behavior represents precisely the point of minimal information loss—neither convergence nor divergence—and thus a balance between adaptability and stability.
To quantitatively study this tradeoff, we required a means of measuring the difference in the information content of two different system states so that we could examine whether this information tends to get attenuated or amplified by the dynamical system. Our basic tool, and a recent development in the field of information theory, is the universal information distance (27, 28), which can be applied to any two objects stored on a computer (e.g., networks, genome sequences, or in our case, macrophage system states). This distance uniquely specifies the informational difference between two objects and is defined in terms of the Kolmogorov complexity. The Kolmogorov complexity, K(x), of an object x is defined to be the length of a shortest program to output x on a universal computer (i.e., on an “all-purpose” machine) (29). Intuitively, K(x) represents the minimal amount of information required to generate x by any effective process and can be thought of as the ultimately compressed form of x.
Although the universal information distance, like the Kolmogorov complexity itself, is not computable, it can nonetheless be approximated by real-world data compressors (herein, gzip) to yield the normalized compression distance (NCD) (28, 30), defined as
where C(x) is the compressed size of x and xy is the concatenation of the strings x and y. It is easy to see that if x and y are identical, then C(x) = C(y) and because it is trivial to compress two identical strings, C(xy) = C(x) = C(y), resulting in the NCD being close to zero. At the other extreme, if x and y are random and independently generated from the same distribution, then C(x) ≈ C(y) and C(xy) ≈ C(x) + C(y), resulting in the NCD being close to one. Cilibrasi and Vitányi (30) have demonstrated that the NCD can be used for clustering a variety of datasets with remarkable success, approximating the provable optimality of the (theoretical) universal information distance.
Analysis of Macrophage Information Dynamics
To study the information flow in the macrophage, we used time-course transcriptional measurement data from murine bone marrow-derived macrophages treated with six TLR agonists: lipopolysaccharide (LPS), PAM2, PAM3, poly(I·C), R848, and unmethylated CpG-containing oligodeoxynucleotide, representing different pathogen-associated molecular patterns (PAMPs). Each time-course experiment consisted of five time-point measurements (ten for LPS) and was biologically replicated two to four times, depending on the stimulus, yielding a total of 35 network state measurements (consisting of 9,941 differentially expressed genes) from a total of 94 microarrays after combining replicates [see supporting information (SI) Appendix for details].
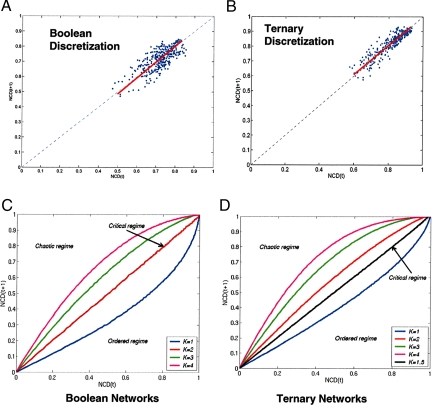
We then computed the NCD for every pair of time-point measurements for which there are successor time-point pairs, and we plotted it versus the NCD computed from the successor states. For example, the NCD between the two time-point measurements, say, LPS/20 min and PAM2/40 min, would be plotted against the NCD between the measurements LPS/40 min and PAM2/60 min, respectively. This procedure allows us to observe how the difference between the information content of any two system states, possibly in response to different stimuli, changes over time. Because NCD is normalized to be in the range [0, 1], a scatter plot that lies below the main diagonal would indicate a general tendency for informational convergence or ordered behavior. Conversely, a scatter plot above the main diagonal would indicate divergence or chaotic behavior. Our main result (Fig. 1 A and B) is that this scatter plot lies closely along the main diagonal with a slope of 1, indicating that the underlying dynamical network of the macrophage is operating in the critical regime.
Fig. 1.
Estimated information-based measure of order and chaos for gene expression in murine macrophage cells stimulated with various TLR-like stimuli. (A and B) The measure is discretized into two (A) and three (B) expression levels (k-means). The x axis value of each data point is the NCD between two expression states. The y axis value of a data point is the NCD of the expression states for the same two experiments at the next time point of the experiment. The red line shows the least-squares fit of the data points, with residual distances being orthogonal to the main diagonal. The data show critical behavior for both binarized and ternarized expression data sets. (C and D) Information-based measure for order and chaos computed for random Boolean networks (K = 1, 2, 3, 4; K = 2 corresponds to the critical regime) (C), and random ternary networks (K = 1, 1.5, 2, 3, and 4; K = 1.5 corresponds to the critical regime) (D).
MATLAB (MathWorks) implementation of the data analysis algorithms is available from the authors upon request.
Validation of the Information Theoretic Order Parameter
The slope of this scatter plot can be considered as an information-based measure of order and chaos that closely parallels the well known Derrida curve (16, 31) in Boolean networks and the Lyapunov exponent (23) in continuous dynamical systems. However, such order parameters are defined in terms of the system's response to only the smallest perturbations, making their use with gene expression data problematic. For example, the Derrida curve, which consists of plotting the Hamming distance (the number of bits that are different) between two states at time t versus the Hamming distance between their successor states at time t + 1, is only indicative of the system's dynamical regime by its slope at the origin. An additional difficulty is that the Hamming distance is only meaningful in the binary domain, and a different measure would need to be used for, say, ternarized data. By contrast, the NCD-based approach used here can be used as is, because it only captures the relative information flow between states and their successors. See SI Appendix for an extended discussion of these issues and a plot of the Hamming distance-based Derrida curve applied to the macrophage data, which also supports critical behavior.
We performed four different studies to validate our approach. First, to be sure that our conclusions were not biased by the number of discretization levels, we performed our analysis with binary as well as ternary discretization (Fig. 1 A and B). It was important to demonstrate criticality with both binary and ternary discretization levels to verify that the somewhat arbitrary choice of discretization level did not affect the results. Second, we repeated the analysis by using two different methods of combining biological replicates. In all cases, we obtained consistent results (see SI Appendix). Third, we decided to determine whether the particular time sampling of our microarray data could affect the conclusions of the analysis. On the basis of a simulation analysis, we found that ordered, chaotic, or critical behavior can be observed over arbitrary time steps (see SI Appendix). Finally, it was necessary to validate the approach in classes of Boolean and ternary networks for which there are well established notions of ordered, chaotic, and critical dynamics (32). Different degree distributions and their known parameter values were used to generate networks in ordered, chaotic, and critical regimes. We found that the measure correctly determined the dynamical regimes for all network ensembles tested (Fig. 1 C and D), with results for additional topologies and degree distributions in SI Appendix. Thus, our approach was validated by each of these studies.
To be convinced that no artifact or trivial reason was behind the data being clustered around the criticality line, we decided to see whether noncritical behavior could be attained by disabling a key regulator of the TLR-mediated response of the macrophage. There are two ways that a departure from criticality could happen. Either the system may no longer be able to respond to certain external information, making the observed responses ordered or relatively insensitive to stimuli, or the system may no longer be able to control its response, rendering it chaotic or hypersensitive to stimuli. To test these alternatives, we performed the NCD-based analysis on an additional time-course data set from macrophages in which an important immune regulator (ATF3) has been knocked out. ATF3 was recently shown to be a negative regulator of the innate immune response, and ATF3−/− macrophages exhibited a significantly amplified pro-inflammatory response as measured by the increased production of several cytokines (33). Further, ATF3−/− mice were more susceptible to endotoxic shock and succumbed much more quickly than wild-type mice when challenged with LPS. The NCD-based analysis indicated that the response of ATF3−/− macrophages to the selected pathogen-associated molecular patterns deviated from criticality in a statistically significant manner, displaying slightly chaotic dynamics (see SI Appendix). This finding demonstrates that noncritical behavior can be observed with this type of analysis.
Conclusions
Our information-based approach revealed that the macrophage exhibits critical dynamics as reflected by global gene expression changes and thus demonstrates its ability to coordinate complex behavior with minimal information loss. The competing selection pressures on the macrophage to have diversity of immune responses yet maintain homeostatic stability must have caused it to evolve the specific dynamic trait of criticality. It will be important to study the evolutionary mechanisms that could have given rise to critical behavior in biological systems (34). Our study also highlights the utility of information-theoretic approaches for analyzing complex biological systems in circumstances where global and detailed quantitative measurements of system behavior are not available or may not be possible to generate.
Supplementary Material
ACKNOWLEDGMENTS.
This work was supported by National Institutes of Health grants GM070600 (I.S. and S.A.K.), GM072855 (I.S.), and P50 GM076547 (L.H. and I.S.); Consejo Nacional de Ciencia y Tecnología Grant P47836-F and Programa de Apoyo a Proyectos de Investigación e Innovación Grant IN-112407–3 (M.A.); Academy of Finland Projects 213462 (O.Y.-H.) and 120411 and 122973 (M.N.); and American Cancer Society Grant PF-06-062-01-MGO (N.D.P.).
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/cgi/content/full/0711525105/DC1.
References
- 1.Murray JD. Mathematical Biology. New York: Springer; 2002. [Google Scholar]
- 2.Nicolis G, Prigogine I. Self-Organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations. New York: Wiley; 1977. [Google Scholar]
- 3.Beekman M, Sumpter DJT, Ratnieks FLW. Phase transition between disordered and ordered foraging in Pharaoh's ants. Proc Natl Acad Sci USA. 2001;98:9703–9706. doi: 10.1073/pnas.161285298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kelso JAS, Bressler SL, Buchanan S, DeGuzman GC, Ding M, et al. A phase transition in human brain and behavior. Phys Lett A. 1992;169:134–144. [Google Scholar]
- 5.Takayasu M, Takayasu H, Fukuda K. Dynamic phase transition observed in the Internet traffic flow. Physica A. 2000;277:248–255. [Google Scholar]
- 6.Bak P, Tang C, Wiesenfeld K. Self-organized criticality: An explanation of the 1/f noise. Phys Rev Lett. 1987;59:381–384. doi: 10.1103/PhysRevLett.59.381. [DOI] [PubMed] [Google Scholar]
- 7.Bak P. How Nature Works: The Science of Self-Organized Criticality. New York: Copernicus; 1996. [Google Scholar]
- 8.Linkenkaer-Hansen K, Nikouline VV, Palva JM, Ilmoniemi RJ. Long-range temporal correlations and scaling behavior in human brain oscillations. J Neurosci. 2001;21:1370–1377. doi: 10.1523/JNEUROSCI.21-04-01370.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Valverde S, Sole RV. Self-organized critical traffic in parallel computer networks. Physica A. 2002;312:636–648. [Google Scholar]
- 10.Fukuda K, Takayasu H, Takayasu M. Origin of critical behavior in Ethernet traffic. Physica A. 2000;287:289–301. [Google Scholar]
- 11.Lux T, Marchesi M. Scaling and criticality in a stochastic multi-agent model of a financial market. Nature. 1999;397:498–500. [Google Scholar]
- 12.Malamud BD, Morein G, Turcotte DL. Forest fires: An example of self-organized critical behavior. Science. 1998;281:1840–1842. doi: 10.1126/science.281.5384.1840. [DOI] [PubMed] [Google Scholar]
- 13.Kinouchi O, Copelli M. Optimal dynamical range of excitable networks at criticality. Nat Phys. 2006;2:348–351. [Google Scholar]
- 14.Sneppen K, Bak P, Flyvbjerg H, Jensen MH. Evolution as a self-organized critical phenomenon. Proc Natl Acad Sci USA. 1995;92:5209–5213. doi: 10.1073/pnas.92.11.5209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Underhill DM, Ozinsky A. Phagocytosis of microbes: Complexity in action. Annu Rev Immunol. 2002;20:825–852. doi: 10.1146/annurev.immunol.20.103001.114744. [DOI] [PubMed] [Google Scholar]
- 16.Kauffman SA. The Origins of Order: Self Organization and Selection in Evolution. New York: Oxford Univ Press; 1993. [Google Scholar]
- 17.Serra R, Villani M, Semeria A. Genetic network models and statistical properties of gene expression data in knock-out experiments. J Theor Biol. 2004;227:149–157. doi: 10.1016/j.jtbi.2003.10.018. [DOI] [PubMed] [Google Scholar]
- 18.Shmulevich I, Kauffman SA, Aldana M. Eukaryotic cells are dynamically ordered or critical but not chaotic. Proc Natl Acad Sci USA. 2005;102:13439–13444. doi: 10.1073/pnas.0506771102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ramo P, Kesseli J, Yli-Harja O. Perturbation avalanches and criticality in gene regulatory networks. J Theor Biol. 2006;242:164–170. doi: 10.1016/j.jtbi.2006.02.011. [DOI] [PubMed] [Google Scholar]
- 20.Barabasi AL, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 21.Albert R, Jeong H, Barabasi AL. Error and attack tolerance of complex networks. Nature. 2000;406:378–382. doi: 10.1038/35019019. [DOI] [PubMed] [Google Scholar]
- 22.Bornholdt S. Systems biology. Less is more in modeling large genetic networks. Science. 2005;310:449–451. doi: 10.1126/science.1119959. [DOI] [PubMed] [Google Scholar]
- 23.Sprott JC. Chaos and time-series analysis. Oxford: Oxford Univ Press; 2003. [Google Scholar]
- 24.Brandman O, Ferrell JE, Jr, Li R, Meyer T. Interlinked fast and slow positive feedback loops drive reliable cell decisions. Science. 2005;310:496–498. doi: 10.1126/science.1113834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ma'ayan A, Jenkins SL, Neves S, Hasseldine A, Grace E, et al. Formation of regulatory patterns during signal propagation in a mammalian cellular network. Science. 2005;309:1078–1083. doi: 10.1126/science.1108876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li F, Long T, Lu Y, Ouyang Q, Tang C. The yeast cell-cycle network is robustly designed. Proc Natl Acad Sci USA. 2004;101:4781–4786. doi: 10.1073/pnas.0305937101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bennett CH, Gacs P, Li M, Vitányi PMB, Zurek WH. Information distance. IEEE T Inform Theory. 1998;44:1407–1423. [Google Scholar]
- 28.Li M, Xin C, Xin L, Bin M, Vitányi PMB. The similarity metric. IEEE T Inform Theory. 2004;50:3250–3264. [Google Scholar]
- 29.Li M, Vitányi PMB. An Introduction to Kolmogorov Complexity and Its Applications. New York: Springer; 1997. [Google Scholar]
- 30.Cilibrasi R, Vitányi PMB. Clustering by compression. IEEE T Inform Theory. 2005;51:1523–1545. [Google Scholar]
- 31.Derrida B, Pomeau Y. Random networks of automata: A simple annealed approximation. Europhys Lett. 1986;1:45–49. [Google Scholar]
- 32.Aldana M, Coppersmith S, Kadanoff LP. In: Perspectives and Problems in Nonlinear Science. Kaplan E, Marsden JE, Sreenivasan KR, editors. New York: Springer; 2002. pp. 23–89. [Google Scholar]
- 33.Gilchrist M, Thorsson V, Li B, Rust AG, Korb M, et al. Systems biology approaches identify ATF3 as a negative regulator of Toll-like receptor 4. Nature. 2006;441:173–178. doi: 10.1038/nature04768. [DOI] [PubMed] [Google Scholar]
- 34.Bornholdt S, Rohlf T. Topological evolution of dynamical networks: Global criticality from local dynamics. Phys Rev Lett. 2000;84:6114–6117. doi: 10.1103/PhysRevLett.84.6114. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.