Two Characteristic Regimes in Frequency-Dependent Dynamic Reorientation of Fibroblasts on Cyclically Stretched Substrates

Abstract

Cells adherent on a cyclically stretched substrate with a periodically varying uniaxial strain are known to dynamically reorient nearly perpendicular to the strain direction. We investigate the dynamic reorientation of rat embryonic and human fibroblast cells over a range of stretching frequency from 0.0001 to 20 s⁻¹ and strain amplitude from 1% to 15%. We report quantitative measurements that show that the mean cell orientation changes exponentially with a frequency-dependent characteristic time from 1 to 5 h. At subconfluent cell densities, this characteristic time for reorientation shows two characteristic regimes as a function of frequency. For frequencies below 1 s⁻¹, the characteristic time decreases with a power law as the frequency increases. For frequencies above 1 s⁻¹, it saturates at a constant value. In addition, a minimum threshold frequency is found below that no significant cell reorientation occurs. Our results are consistent for the two different fibroblast types and indicate a saturation of molecular mechanisms of mechanotransduction or response machinery for subconfluent cells within the frequency regime under investigation. For confluent cell layers, we observe similar behaviors of reorientation under cyclic stretch but no saturation in the characteristic time with frequency, suggesting that cell-cell contacts can play an important role in the response machinery of cells under mechanical strain.

INTRODUCTION

Mechanical signals play important roles in many fundamental cell functions, influencing for example, the proliferation, differentiation, and migration of cells and thereby regulating important processes such as bone and cartilage growth, wound healing, and angiogenesis (1). These processes depend on the responses of cells to mechanical forces generated either by the contractile cytoskeleton-motor protein complex of the cells themselves or by external stresses (2–4). Many aspects of biochemical mechanotransduction and subsequent responses are not known in detail, yet a profound understanding of cell responses to mechanical signals is important for basic biological science (5,6).

Different methods have been developed to investigate the influence of mechanical signals on cells (7). One common method of examining cell responses to mechanical stress is the use of flexible membranes as culture substrates (8,9). Cells adherent on an expandable elastomeric substrate coated with extracellular matrix molecules like fibronectin or collagen can be exposed to a mechanical strain (10). One general experimental observation is that cells respond differently when the substrate is subjected to a constant static strain as compared to a periodically varying strain. For static strain, cells tend to align themselves parallel to the direction of stretch (11,12). In contrast, several studies have shown that cells on cyclically stretched substrates tend to reorient themselves nearly perpendicular to the direction of stretch (10,13–19). At the same time, the actin cytoskeleton is reorganized perpendicular to the stretch direction (20–22). Such an orientation response has been found in many different cell types such as endothelial cells, osteoblasts, or fibroblasts. The results support the common hypothesis that cell alignment is an avoidance reaction of the cells to stretching via interactions with the extracellular matrix by focal contacts and their mechanical link to the cytoskeleton (23). Despite many experimental studies, only limited information about the dynamics of cell reorientation is available to this date, due partly to experimental limitations with life-cell imaging. For example, Neidlinger-Wilke et al. (18) showed that fibroblasts tend to reorient within the first 3 h during cyclic stretch. Liu et al. (24) showed a frequency dependence for the alignment of arterial smooth muscle cells observed in time steps of 3 h. There is still a lack of detailed quantitative examination of the temporal behavior of cells under cyclic stretch, although such information could be helpful for understanding the molecular mechanisms involved and is crucial for theoretical modeling (25). This study is aimed at investigating the effects of strain frequency and strain amplitude on the temporal dynamics of cell reorientation. We conducted experimental measurements with high temporal resolution and show a novel biphasic behavior of the characteristic time of cell reorganization in the frequency range from 0.0001 to 20 s⁻¹. This biphasic behavior, which is characteristic of both types of fibroblast cells at subconfluent densities, was not observed in experiments on a confluent layer of cells, suggesting that cell-cell contacts can play an important role in mechanosensing (4,26,27). In addition to these novel results on the frequency dependence, we also examined the temporal response at different strain amplitudes. Previous studies of Neidlinger-Wilke et al. (28) showed that the final degree of perpendicular cell alignment increases with the stretch amplitude and Dartsch et al. (13) observed a certain threshold amplitude between 2% and 3.5% below which no reorientation occurred for smooth muscle cells. For the first time, to our knowledge, we found a linear dependence of the characteristic time of cell reorientation on the strain amplitude. We believe our results provide new insights into the behaviors of cells under cyclic stretch by showing both threshold and saturation strain frequencies, as well as a threshold strain amplitude characteristic of cell responses to mechanical signals. These critical values should be based on limitations in molecular mechanisms that are still not fully understood. Our results may motivate further development and verifications of several physical models on cell reorientation (25,29–32).

MATERIALS AND METHODS

Cell culture

As model systems, we used two different fibroblast cell types, REF 52 cells (rat embryonic fibroblasts) and HDF cells (human dermal fibroblasts). Both cell types were cultured in Dulbecco modified Eagle's medium (Gibco Laboratories, Eggenstein, Germany) supplemented with 10% fetal bovine serum and 2 mM L-glutamin (Gibco) at 37°C and 5% CO₂. REF cells were kindly provided by Benjamin Geiger (Weizmann Institute of Science). The HDF cells were kindly provided by Dieter Kaufmann (University of Ulm). Only HDF cells of low passage number between 4 and 12 were used. The cells were cultured in 25 cm² flasks (Nunc, Roskilde, Denmark) until a subconfluent stage was reached. The media was changed every 2–3 days and for detaching, 0.25% trypsin/1 mM ethylenediaminetetraacetic acid was used.

Cell stretching device and experiment

A customized stretching device was developed in our laboratory to apply periodical mechanical strain to an elastomeric membrane that served as cell culture substrate. The setup consists of two brushless servo motors (Faulhaber, Schönaich, Germany) allowing for stretching the membrane via a mechanical construction of eccentric tappets and con-rods. To move the whole setup in x and y direction, the device is attached on a manual self-made x-y stage. The stretching device is mounted on a motorized inverted light microscope (Axiovert 200M, 10×/0.25Ph1 objective, Zeiss, Jena, Germany) that is equipped with a CCD-camera (PCO Sensicam, Kelheim, Germany). The microscope is placed inside an environmental chamber to control temperature and CO₂ concentration of the atmosphere. The stretching device, the motorized components of the microscope, and the image acquisition by the camera are controlled by a self-developed software routine embedded in Image Pro 6.2 (Media Cybernetics, Bethesda, MD).

The cells were plated on a 20 × 20 mm poly(dimethylsiloxane) (PDMS) (Sylgard 184, Corning, Midland, MI) membrane with an elastic modulus of ∼1 MPa. The suitability of PDMS dishes for cell culture was shown for example by Neidlinger-Wilke et al. (10) and Lee et al. (33). The chamber is made by casting PDMS in a plexiglas mold at a ratio of elastomer and cross linker of 10:1. After curing for 12 h (65°C), the deformable chamber is clamped in the custom-made stretching device designed for periodic stretching of the membrane in one direction (uniaxial strain). The periodic strain is set to be always tensile with a magnitude equal to A=A₀ (1+ sin2πft)/2, thus having no compression phase in the loading process. A₀ is the maximum amplitude, f the stretching frequency (Fig. 1). Dirt on the membrane surface and polystyrene beads were used to measure the homogeneity of the strain field in the center region of the membrane before each experiment. Measurements were done in the relaxed and stretched states of the membrane. To check if the stretch is transferred to the cells adhering on the surface, deformation of the cells were also measured in both relaxed and stretched states. Analysis of the strain field was carried out by Image Pro measuring several displacement vectors.

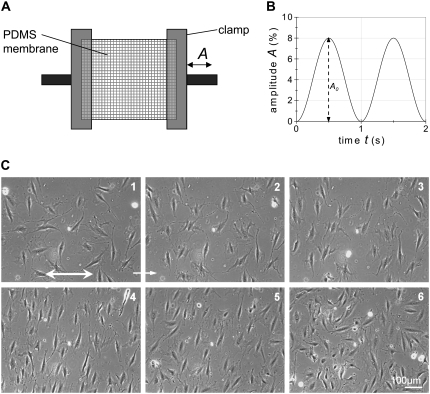
FIGURE 1.

(A) Schematic drawing of the experimental setup. An elastic membrane is clamped and periodically elongated in x direction with the time-dependent amplitude A. The time-course of A is given in (B) as an example with the maximal amplitude A₀ = 8% and a frequency f = 1 s⁻¹. (C) Light microscopy image sequence of REF cells adhering to a cyclically stretched substrate at strain amplitude A = 8% and strain frequency f = 10 s⁻¹. Each image corresponds to a particular time, t, after the start of stretching: 1 (t = 0); 2 (t = 30 min); 3 (t = 100 min); 4 (t = 500 min); 5 (t = 625 min); 6 (t = 1050 min). The substrate was stretched in the x-direction (double arrow in image 1). After 500 min (4) the applied stretch was stopped and the subsequent relaxation was observed (5 and 6). The cell number increases in the course of the experiments due to cell division and the cells migrate (see Movie S1).

Before the experiments, the stretching chambers were sterilized with ethanol and washed several times with phosphate buffered saline, and were incubated overnight (12–14 h) with a 5 μg/ml Fibronectin solution (Sigma). The HDF cells were plated at a density of 50 cells/mm², whereas the REF52 cells were plated at two different cell densities: a subconfluent density of 50 cells /mm² and a confluent layer of 100 cells/mm². To avoid bacteria contamination, 100 U/mL of penicillin-streptomycin (Gibco) was added to the medium. The cells were cultivated on the substrates for 24 h before starting the experiments. Markers in the center region of the stretching chambers were used to find the same position on the membrane in all experiments.

The field of view under the microscope gives the possibility to observe between 25 and 30 HDF cells. In the case of REF52, one can observe between 35 and 40 cells at a low density and more than 80 cells at a high density.

A stretching frequency between 0.0001 s⁻¹ and 20 s⁻¹ and a stretching amplitude between 1% and 15%, were selected in each experiment. To avoid wrinkles on the substrate surface, the clamped substrate was set under a small static prestrain. The experiment was started after 2 h, so that the cells could accommodate to the prestrain. During the experiment, the cells were under physiological conditions (37°C, 5% CO₂, high humidity) and phase contrast images were acquired in the nonstrained position at intervals of 100 s. Each image was focused before acquisition by a software-based auto focusing routine. The periodic strain was stopped after 30,000 s and the cells were observed for further 35,000 s.

Image analyses

Cell orientation was measured via the image processing software ImageJ (34). Phase contrast images were taken out from the time-lapse movies and the outline of each cell was marked. Small tethers of the cells were neglected in this process; only the coarse cell body was marked. An image processing macro was used to fit an ellipse to each elongated cell outline. The macro gives results like the orientation angle φ of the long axis of a cell with respect to the strain direction, the minor and major axes of the ellipse, and the total cell area. These data are used to calculate the mean value and SE of, for example, the orientation of cells for each chosen point of time (Origin Lab 7.5, Microcal, Northampton, MA).

Quantification of data

To quantify the cellular response to stretching, the density distribution 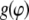of the cell orientation angle and the order parameter (16,35)

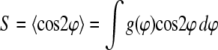(1)

was calculated from the image sequences using between 30 and 50 cells per experiment. It follows from the above definition that 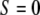if the cells are randomly orientated, 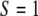if they are parallel oriented, and 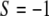if they are perpendicularly oriented with respect to the stretching direction (see Na et al. (37) for further details about the order parameter). Following a procedure based on a stochastic differential equation (16,35) and the definition of this order parameter, we derived from a series the following exponential expression to evaluate the time dependence of the order parameter,

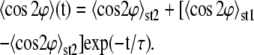(2)

This equation indicates that, starting at a stationary state 〈cos 2φ〉_st1, a new steady state 〈cos2φ〉_st2 is reached over a characteristic time τ of dynamic cell reorientation. In our experiments the characteristic time τ was determined by matching Eq. 2 to the experimental data via a least-square fit using Origin Lab software (Microcal).

RESULTS

Verification of strain field

The characterization of the strain field in the center region of the PDMS surface showed an almost homogeneous strain distribution. The stretching of the membrane creates a biaxial strain at the center described by a longitudinal elongation and a transverse contraction. At strain amplitudes of 2%, 6%, 8%, 12.5%, and 15%, the measured values of strain are close to those expected of the specific eccentric tappets. For instance, a theoretical applied strain of 8% resulted in a measured longitudinal elongation of 7.99 ± 0.7%, with a transverse contraction of 1.55 ± 0.1%. Measurements of the most distant points of typical cell outlines parallel and perpendicular to the strain direction in both relaxed and strained positions yield a longitudinal cell elongation of 7.54 ± 0.7% and a cell contraction of 0.99 ± 0.1%. These values are appropriate and the ratio between the elongation and contraction is almost constant.

Time course of reorientation

Cells of both types, REF and HDF, adhering to the elastomeric substrates were initially oriented in random directions, corresponding to an initial order parameter around S = 0, with slight fluctuations similar to that seen in the control experiments without an applied strain. The fluctuations resulting from random migrations of cells typically have an amplitude smaller than S = 0.2.

Starting the stretching experiment, the cells began to orient themselves perpendicular to the uniaxial stretching direction (Fig. 1, images 1–4). The cell density increases due to cell divisions during the experiment and cells migrate that can be seen in the time lapse movie (Supplementary Material, Movie S1). After the periodic strain was stopped at t = 30,000 s (Fig. 1, image 5 and 6), we found that the REF cells started to realign in random directions. In contrast, the HDF cells remained perpendicular to the strain direction over the full observation time of 35,000 s.

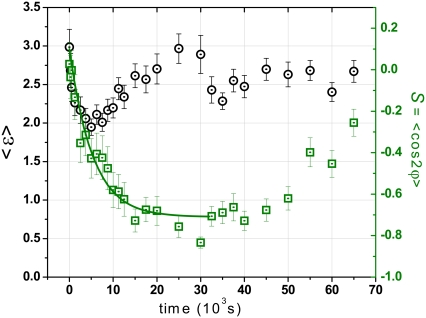
One representative example of cell alignment is shown in Fig. 2, where the mean order parameter S and mean cell elongation 〈ɛ〉 (average of the ratio between the major and minor axes of an elliptical cell outline) are plotted as a function of time to show the dynamic evolution of the shape and orientation of the cells. Initially, the orientation of the cell ensemble is nearly random (S ≈ 0) and the mean cell elongation is 〈ɛ〉 ≈ 3. After the periodic strain is switched on (f = 2 s⁻¹, A = 8%), the cells became slightly rounded with a smaller elongation of 〈ɛ〉 ≈ 2 in the first 100 min. After this period, the cells started to elongate again in a new direction to a mean elongation of about 〈ɛ〉 = 3.0. When the periodic stretching is switched off after 30,000 s, the mean elongation decreases to a new stationary value of ∼2.7. The order parameter S changes in correlation with 〈ɛ〉 as the cells change their orientation perpendicular to the applied strain. Correspondingly, S changes exponentially from an initial value of S ≈ 0.08 to a new steady state order parameter of S ≈ −0.75. After the periodic strain was stopped, we observed a random migration of the REF cells in random orientations. In contrast, the HDF cells showed qualitatively similar behaviors as long as the periodic strain is applied; however, hardly any reorientation of the HDF cells occurs after the strain was stopped.

FIGURE 2.

Evolution of the mean elongation 〈ɛ〉 (○) and the orientation order parameter S (□) as a function of time for REF cells on cyclically stretched substrate at strain frequency f = 2 s⁻¹ and amplitude A = 8%. The strain was applied at 0 s and stopped after 30 × 10³ s.

Dependence on strain frequency

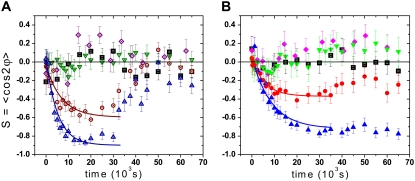
To investigate the frequency-dependence of cell response, we measured the characteristic time for various strain frequencies from 0.0001 s⁻¹ to 20 s⁻¹. In particular, we applied cyclic strains of frequencies at 0.0001 s⁻¹, 0.001 s⁻¹, 0.01 s⁻¹, 0.05 s⁻¹, 0.1 s⁻¹, 0.25 s⁻¹, 0.5 s⁻¹, 1.0 s⁻¹, 2.0 s⁻¹, 5.0 s⁻¹, 10.0 s⁻¹, and 20.0 s⁻¹. Typical examples for the dynamic change of the order parameter as a function of frequency are shown in Fig. 3. The orientation change occurs faster at high frequencies (Fig. 3, triangles) than at low frequencies (Fig. 3, circles), and the new steady state value of S is higher at higher frequencies. Below a certain threshold frequency f_t1, depending on the cell type, we found that the cells no longer respond to the cyclic stretching and no reorientation is observed (Fig. 3, down triangles); in this case, the cell response is comparable to that in the control experiment where the mean cell orientation fluctuates around S = 0 (Fig. 3, squares). Only at frequencies higher than the threshold value (f > f_t1) do cells change to a perpendicular orientation with time (Fig. 3, circles and up triangles). The observed threshold frequency seemed to be cell-type dependent: it was found to be f_t1 ≈ 0.01 s⁻¹ for the REF cells and f_t1 ≈ 0.1 s⁻¹ for the HDF cells (Fig. 3, down triangles). Experiments with frequencies smaller than f_t1, which means from 0.01 s⁻¹ to 0.0001 s⁻¹ for the REF cells and from 0.1 s⁻¹ to 0.0001 s⁻¹ for the HDF cells, did not generate a significant reorientation response. This observation holds true for both cell densities of 50 cells/mm² and 100 cells/mm² as shown in Fig. 3 A (diamonds).

FIGURE 3.

Exponential decrease of the order parameter S from a random orientation (S ≈ 0) to a saturation value at different stretching frequencies (A, REF cells; B, HDF cells). Four frequencies are considered for each type of cells taking into account 30–50 cells per experiment. For REF cells, we considered 0.25 s⁻¹(○) and 15 s⁻¹ (Δ), at which the cells actively reoriented perpendicular to the strain direction, and the threshold frequency 0.01 s⁻¹ (∇) and the lowest frequency 0.0001 s⁻¹ (⋄), at which the cells did not show significant response to the cyclic strain. For HDF cells, we considered two active frequencies 0.5 s⁻¹ (circle) and 20 s⁻¹ (up triangle), the threshold frequency 0.1 s⁻¹ (down triangle) and the lowest frequency 0.0001 s⁻¹ (diamond). The data for control experiments (▪) with no mechanical strain are plotted for comparison. Error bars are the SD of the mean value. The characteristic time τ is determined via an exponential fit of the experimental curves. Note that the REF cells return to random alignment whereas the HDF cells stay in perpendicular direction after the stretching is switched off (t = 30 × 10³ s). The cell density is 100 cells/mm² at f ≈ 0.0001 s⁻¹ for the REF cells and 50 cells/mm² for all other frequencies.

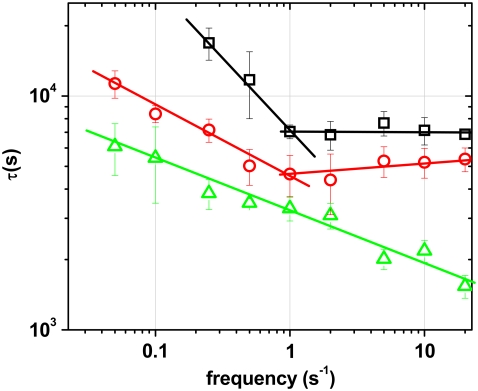
All experimental data were fitted with the exponential expression given in Eq. 2. The results for experiments with frequencies between the lower threshold f_t1 and 20 s⁻¹ shows two distinct regimes for the characteristic time τ for both cell types (Fig. 4) seeded at a subconfluent density. A frequency dependent regime with a power law decrease of τ is followed by a nearly constant regime where an increase in f no longer induces a faster response. This biphasic behavior of the temporal response is universal for both cell types as shown in Fig. 4. The threshold frequency f_t2 between the two phases is ∼1 s⁻¹ for both cell types (Fig. 4). Although the general features of the biphasic temporal behavior are similar for both cell types, the REF cells respond significantly faster than the HDF cells at all frequencies.

FIGURE 4.

Biphasic characteristics of dynamic cell reorientation for subconfluent cells (□ and ○). The characteristic time τ decreases for f < 1 s⁻¹ and then remains constant for f > 1 s⁻¹. Reorientation of HDF cells (□) is slower than that of REF cells (○) for all frequencies. The threshold frequency for the onset of cellular response is higher for the HDF cells than for the REF cells. At higher cell density (confluent), the characteristic time continues to decrease with a power law and shows no constant regime (▵).

For a confluent cell layer with cell-cell contacts, we did not observe the biphasic temporal behavior. The characteristic time continued to decrease with a power law up to the frequency of 20 s⁻¹, with no saturation visible (Fig. 4, triangle), i.e., an increase in frequency always leads to a faster reorientation. The threshold frequency of f_t1 ≈ 0.01 s⁻¹ seems to be independent of cell density for the REF cells. The confluent REF cells returned to random orientations after the periodic stretch was stopped.

Dependence on strain amplitude

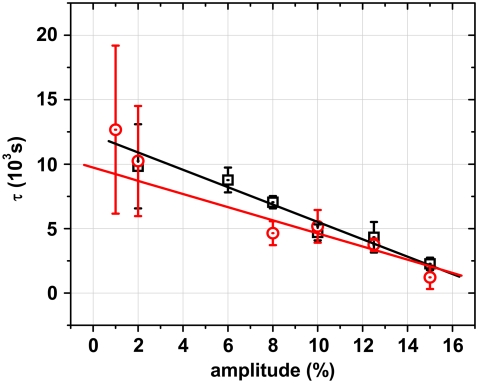
Besides the observed frequency dependence of reorientation during cyclic stretch for different cell types and cell densities, we also examined the effect of stretching amplitude on reorientation. The change of the order parameter in these experiments looks similar to that shown in Fig. 3. However, there is no significant difference in the time course of reorientation between REF and HDF cells for all strain amplitudes. For both cell types, the characteristic time for the change in S depends linearly on the strain amplitude as shown in Fig. 5. The reorientation happens faster at higher strain amplitudes. The reorientation time is about 10 times faster at a strain amplitude of 15% than at 2%. Independent of the strain amplitude, the orientations of the REF cells returned to random after the strain is stopped, whereas the HDF cells remained in the perpendicular orientation. The threshold amplitude below that no cellular orientation response was observed is 1% for the REF cells and 2% for the HDF cells.

FIGURE 5.

The characteristic time τ of cell reorientation decreases linearly as a function of strain amplitude at a strain frequency of 1 s⁻¹. The threshold amplitude for reorientation is 2% for the HDF cells (□) and 1% for the REF52 cells (○). The effect of strain amplitude is similar for both cell types.

DISCUSSION

Research during the last decades has identified various effects of periodic stretch on cells, including cell reorientation and cytoskeleton modification (10,13–22). In particular, the effect of strain amplitude on cell reorientation has been identified but only a few studies examined the frequency dependence of cell orientation response. Kaspar et al. (36) investigated if the number of applied load cycles and the frequency of uniaxial strain have an effect on proliferation of human osteoblast-like cells. Using a periodic stimulus for bone cells, they found a frequency and cycle number dependent proliferative response of human osteoblast-like cells with an optimal frequency of 1 Hz. Liu et al. (24) noted that smooth muscle cells stretched with the same amplitude showed changes in alignment depending on the tested frequencies of 0.5 s⁻¹, 1 s⁻¹, 1.5 s⁻¹, and 2 s⁻¹. They concluded that the frequency is an important regulatory factor for smooth muscle cell alignment and served as an independent signal from amplitude and duration. Their studies, however, did not measure the time course of reorientation in detail with rather crude time steps of several hours. In our study, rat and human fibroblasts were stretched with the different magnitudes at a specific duration of cyclic strain (∼8 h), and different stretching frequency. Using an order parameter to quantify the cell orientation, we could show that the dynamic orientation of the cells perpendicular to the stretch direction depends on the frequency. In addition, we achieved a very high time resolution by carrying out the experiments on top of a microscope. In contrast, other studies typically observe only one time point at the end of the experiments (10,15) or carried out experiments with low temporal resolution of many minutes (18,22). To our knowledge, this study is the first detailed study of the effects of stretching amplitude and frequency on the temporal dynamics of cell reorientation on a cyclic stretched substrate.

Exponential behavior in cell reorientation

Cell reorientation requires a continuous remodeling of focal adhesions and actin cytoskeleton (22,37,38). The actin stress fibers need to be depolymerized and polymerized in a new direction to establish a new equilibrium after an adaptive process. Similar processes are required for the focal adhesions. A continuous remodeling of focal adhesion sites is needed in cell migration, reorientation and shape changes. The temporal dynamics of these processes should correspond with the exponential time course of reorientation observed in our experiments. Cells in our experiments became slightly rounded in the beginning of reorientation but elongated again in a new direction around the characteristic time of reorientation. The onset of these processes is visible within a few minutes (Fig. 2) and last between 60 and 120 min for the REF cells when cells reached a new steady state in the cell orientation. This is consistent with observation of focal adhesion remodeling within minutes after applying a cyclic stretch to vascular smooth muscle cells observed by Na et al. (37). They observed an increase in cell stiffness within 2 min and suggest that this is due to an increase in stretch of the original stress fibers and partially to the assembly of new less stretched stress fibers. In the further progress (30 min) they suggest an increasing replacement of highly prestressed fibers with new less stretched filaments consistent with a decrease in cell stiffness. The newly formed stress fibers are orientated perpendicular to the stretch as observed by other groups if a cyclic stretch is applied. Hayakawa et al. (22) observed a perpendicular reorganization of actin stress fibers of rat smooth muscle cells within a time of 45–60 min similar to observation with endothelial cells by Yoshigi et al. (39) that also observed a higher density of stress fibers after 30 min. For the same cell type a similar result for the time for reorientation of actin stress fiber was obtained by Katsumi et al. (40), however, they applied a static stretch of 8% found an increased orientation in direction of strain after 30 and 60 min. It is assumed that at such time scales a new mechanical “homeostasis” is reached (37). This was also seen in single stretch experiments by Mizutani et al. (41). They observed an instant chance in cellular stiffness in response to a single elongating or compressing, however, recovery to the initial stiffness took 2 h, and then stabilized. This is a comparable time scale to our observed REF cell reorganization in particular if one assumes that actin reorganization occurs before drastic cell shape changes are visible (39,42) and a new steady state is reached exponentially. In addition, differences in reorientation time might result from the use of different cell types. That can be supported by the even slower response of the HDF cells. After adjusting themselves to a new orientation, the cells start to rebuild the cytoskeleton and elongate along the new orientation. For both cell types we get the same characteristic for the dynamic behavior during cyclic stretch. The exponential characteristic is independent of the amplitude or the frequency if both signals are above a certain threshold. The essential features of reorientation are the same for both cell types; however, the threshold frequency f_t1 and the characteristic time of reorientation are significantly different. Our results show that the REF cells have a ten times lower frequency threshold of reorientation than the HDF cells, and reorientation is always faster for REF than for HDF. Measurement of F- and G-Actin content could show if and how much the cells differ in their cytoskeleton constitution (24). Alternatively, a similar approach as carried out by Na et al. (37) could show the differences in initial cell mechanical properties and stiffening and actin filament turnover at cyclic by AFM indention measurements. Further analysis of random migration of cells may also provide some insights in the cytoskeleton turn-around and see if and how it is correlated to the differences observed in our experiments.

Frequency dependence

For a subconfluent cell density of ∼50 cells/mm², we observed two distinctive regimes for the frequency dependence of the characteristic time of reorientation. The characteristic time decreases with a power law from a threshold frequency at which a response first becomes visible to a saturation frequency of ∼1 s⁻¹. For frequencies above 1 s⁻¹, we observed a regime of constant characteristic time in which an increase in frequency does not accelerate cell reorientation. It seems that the molecular machinery of either sensory or actuation type has reached a saturation level at frequencies above 1 s⁻¹ and can not react faster.

One might speculate about the molecular origin of the lower threshold frequency and the saturation frequency f = 1 s⁻¹. Mechanosensing requires by definition an element that responds to an applied mechanical stimulus; however, there is yet to be a fully accepted detailed understanding on what cellular components measure specific mechanical signals (4,6). Elements known to play important roles in response to mechanical signals include cadherin in cell-cell contacts and integrins (and other focal adhesion proteins) in cell-substrate contacts (26,27).

Other studies have shown that the cytoskeletal architecture of cells tends to remodel in response to stretching (22,38), which is an active cellular process controlled by signaling proteins; it has also been shown that the level of Rho activity controls the extent and direction of orientation of stress fibers in stretched cells and thus their elongation. Rho GTPase is known to be activated by integrin triggered pathways (43). It is possible that the Rho pathway activation might have been saturated at frequencies above 1 s⁻¹. Kaunas et al. (38) showed that stress fiber orientation is dependent of both, the amplitude of the stretching and the Rho pathway. Expression of active RhoV14 enhanced the alignment of the stress fibers perpendicular to the strain, with Rho pathway inhibition, stress fiber became aligned parallel to the strain. Ideally, FRET measurements similar to Katsumi et al. (40) could proof the activation of Rho that is supposed to happen early in the response and a possible saturation effect at high frequencies.

Alternatively, the reorganization of focal adhesions and the actin cytoskeleton itself might be a limiting factor. Although typical time scales of focal adhesion formation and actin remodeling are of the order of 3–90 min (39,40,44), stretching may influence directionality of protein polymerization or de-polymerization (22). Fast compression, for example, can lead to disassembly of actin fibers within a minute (45). In contrast to the experiments with subconfluent cell densities (50 cells/mm²), we did not find a two-regime behavior for experiments with a confluent cell layer (100 cells/mm²). In addition, the reorientation time is always shorter for confluent cells than for isolated cells. It seems that in the former case the molecular machinery is not in saturation, which might be due to the fact that cell-cell contacts via cadherins are now present in addition to cell-matrix contacts via integrins. Integrins in focal adhesions are not the only cell membrane sites at which mechanochemical conversion could happen. It is known that mechanical forces can be similarly transmitted to the cytoskeleton by cadherins (26,27,46), thus providing an additional mechanical sensing mechanism if such contacts are present at higher cell densities. Further studies with specific inhibition of one or the other pathway and observation of the reorientation kinetics could prove this hypothesis. It should be mentioned that the increased in reorientation speed at high cell densities would rather proof that the signaling (e.g., by integrins) is in saturation at lower cell densities for frequencies above 1 s⁻¹.

Furthermore, our experiments may be helpful for the further development of biophysically motivated modeling aimed to improve our understanding of mechanically induced cell responses. There is currently no realistic theoretical model for the actual force sensing mechanisms and the internal reorganization of cellular components associated with the cellular response to stretch. On the other hand, a number of initial modeling approaches have been proposed to take into account different degrees of molecular details in predicting certain aspects of the cell orientation in response to periodic stretching (29,30,32,37).

A recent model approach in cell mechanics presents a “tensional homeostasis” assuming that cells try to keep constant certain mechanical properties such as an optimal internal stress (38). Based on such an idea, one model describes the cell as an elastic dipole interacting with a periodic external strain field (25), while assuming that an intrinsic relaxation time exists for the remodeling and readjustment of the cell orientation. This relaxation time is of unknown magnitude and corresponds to the reorganization of actin stress fibers and focal adhesions. The theoretical model of De et al. (25) predicts how the combination of active cellular forces due to i), the reorganization of the cytoskeleton; and ii), the elastic forces exerted by the matrix, determines cellular orientation in the presence of both static and dynamic strains. At high frequencies, the cells align nearly perpendicular to the stress because they do not have sufficient time to relax the forces due to their reorganization; they cannot instantaneously follow the external stress and can only respond to its time average. Therefore, the cell response and the characteristic time are almost frequency independent as seen from our experiments. However, with decreasing frequency, the characteristic time for cell orientation response increases because the cells do have sufficient time to relax and reorganize their cytoskeleton to establish the optimal stress (set point) in the adjacent matrix.

In the low frequency regime, where the cellular orientation is predicted to be more parallel to the external stress, internal cellular relaxation plays a crucial role and eventually sets the characteristic time of the steady state alignment. Our experiments show a qualitative agreement with the theoretical predictions that intuitively explain our observed bi-phasic characteristic frequency regimes (25). We did not detect a significant alignment in the direction parallel to the strain for very low frequencies (0.0001 s⁻¹ and 0.001 s⁻¹), in contrast to other experiments (11,40,47) and model predictions (25). We assume that this difference might be explained by the cellular environment in our experiments where the cells were cultured on rather stiff PDMS substrates (Young's modulus ∼1 MPa) coated with a low concentration of fibronectin whereas Eastwood et al. (11) used a rather thick collagen lattice. The parallel orientation they observed might be due to a mechanical alignment of collagen fibers and subsequent contact guidance of the fibroblast cells (46). However, preliminary experiments in our group with a different cell type (human mesenchymal stem cells) show a parallel orientation at low frequencies that show a cell type specific response. Of course, our experiments can not prove the model but experimental data and model show some consistency and our results may give important insight for further directions of a physical motivated understanding of these cell mechanical phenomena.

Besides the investigation of the frequency dependence of reorientation dynamics, we also studied the effect of strain amplitude on the orientation kinetics at a constant frequency. Previous studies indicated that cells align more perpendicular to the stretch direction with an increase in strain amplitude (16,28), but these studies did not show any data of the reorientation dynamics. In contrast to the biphasic behavior of the characteristic time associated with frequency variation, we did not observe a similar biphasic behavior associated with strain amplitude. Instead, we observed a negative linear relation between the characteristic time and the strain amplitude. No saturation was observed for strains up to 16%. These results may indicate that frequency and amplitude are independent signals for the kinetics of cell response.

In summery, our results show an exponential reorientation characteristics and a biphasic frequency-dependent response to cyclic strain in two cells types. We observed a cell-type dependent lower threshold frequency below which no reorientation occurred and a saturation in temporal response at frequencies above 1 s⁻¹. Our results may provide a basis for further modeling of cellular response to cyclic stretching. Experiments with cells expressing fluorescent-protein tagged actin and focal adhesion proteins should provide further insights into the molecular mechanisms associated with these issues.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.