Peptide Aggregation in Finite Systems

Abstract

Universal features of the peptide aggregation process suggest a common mechanism, with a first-order phase transition in aqueous solutions of the peptides being the driving force. Small system sizes strongly affect the stability of the minor phase in the two-phase region. We show manifestations of this effect in aqueous solutions of fragments of the islet amyloid polypeptide, using computer simulation methods and invoking various approaches in characterizing clustering and aggregate formation. These systems with peptide concentrations deeply inside the immiscibility region show two distinct stable states, which interchange with time: one state contains a peptide aggregate; and the other state has an aggregate that is noticeably dissolved. The first state is relevant for macroscopic systems, whereas the second one is artificial. At a fixed concentration, the occurrence probability of the aggregate state vanishes upon decreasing the system size, thus indicating the necessity to apply a finite size-scaling for meaningful studies of peptide aggregation by simulations. The effect observed may be one of the factors responsible for the difference between intracellular and extracellular aggregation and fibrillization of polypeptides. The finite size of biological cells or their compartments may be playing a decisive role in hampering intracellular aggregation of highly insoluble amyloidogenic proteins, whereas aggregation is unavoidable in the extracellular space at the same peptide concentration.

INTRODUCTION

Aggregation of biomolecules, such as proteins, in aqueous environment is a common phenomenon involved in various biologically important processes. There are many universal features of the aggregation process of proteins in liquid water (1–5). Aggregation is a cooperative process, which occurs when the concentration of the biomolecule exceeds a certain critical value. This critical concentration depends on the chemical structure of the biomolecule, the temperature, ionic strength, pH, etc. The aggregation process shows the features typical for nucleation processes in a system undergoing a first-order phase transition in the two-phase region (such as condensation of an oversaturated vapor). In particular, the lag time of aggregation decreases with increasing concentration or upon adding seeds of the organic-rich (proteinaceous) phase. The aggregation behavior of proteins in liquid water is similar to the demixing phase transition of aqueous solutions of organic molecules. Many aqueous solutions of simple organic molecules (pyridines, tetrahydrofuran, etc.) show demixing upon heating (6,7). Aqueous solutions of large polymeric macromolecules (poly-n-isopropylacrylamide, polyoxyethylene, etc.) also show demixing upon heating, accompanied by drastic changes of the polymer conformation (8–10). Quite similarly, aggregation and precipitation of proteins accompanying (or accompanied by) marked conformational changes also occurs upon heating. Thus, the occurrence of the first-order demixing phase transition in aqueous solutions of proteins may not be surprising, as it is a common phenomenon for binary systems.

Upon demixing, aqueous solutions of organic molecules separate into a water-rich phase and an organic-rich phase. When the thermodynamic conditions are close to ambient conditions, the water-rich phase is a liquid phase. The state of the organic-rich phase depends mainly on the phase state of the corresponding organic substance at ambient conditions. It may be a vapor phase (for example, in water-methane mixture), a liquid phase (for example, in aqueous solutions of pyridines), or an amorphous (solidlike) phase (aqueous solutions of macromolecules). Dry biomolecular substances are typically in an amorphous state at ambient conditions. Therefore, upon demixing, their aqueous solutions separate into a liquid water-rich phase with the critical concentration mentioned above, and a solidlike organic-rich phase, which may be amorphous or ordered (crystalline or fibrillar).

Simulation studies can provide an efficient tool to characterize the aggregation and conformational changes of biomolecules in water at a molecular level. However, any simulation study is unavoidably affected by the finite size of the simulated system, and the evolution of the system properties toward those in the macroscopic limit should be understood and taken properly into account. The possible occurrence of a phase transitions in the system studied must also be taken into account by the choice of an appropriate ensemble. Nowadays, simulation studies of aggregation of biomolecules can be performed only in simple ensembles, such as those with constant volume or constant pressure. Typically, these simulations are performed at conditions of strong oversaturation, i.e., deeply inside the concentration range, where the system undergoes demixing. When the size of the system being in the two-phase state is finite, the behavior of the minor phase noticeably differs from that encountered in the corresponding macroscopic system (11–16). For example, in a macroscopic one-component fluid, the oversaturated vapor separates into coexisting liquid and vapor phases, such as a liquid droplet surrounded by a saturated vapor. When the fluid volume is finite, a new stable state emerges at the same density: an evaporated (at least partially) droplet surrounded by oversaturated vapor. The state with droplet and the state without droplet are both stable and replace each other with time. The occurrence probability of these states is determined by the level of the oversaturation and by the system size. An increase of the system size eventually stabilizes the droplet state, which is the only stable state in the macroscopic limit. A state without droplet is just an artificial state, whose properties have no relation to those expected in the macroscopic limit.

A similar behavior of aqueous solution of peptides in small volumes may be expected at concentrations exceeding the solubility limit. To our knowledge, this factor has not yet been considered in the simulation studies of aggregation phenomena in biosystems. The main goal of our study is to estimate to what extent the finite size of the simulated system distorts the aggregation behavior of the peptides in the simulation studies. A rather small number of biomolecules can be used in simulation studies of aggregation currently, and a full application of the finite size scaling is possible in a long-term perspective, only. Therefore, it is important to find an efficient way to distinguish between the state which is relevant to the macroscopic system and the artificial state caused by the finite system size. This should provide a possibility to account for this distorting effect of the artificial state at least partially. The achievement of this goal requires the development of suitable methods, which allow the characterization of the degree of aggregation of the peptides.

In silico, the finite size of the simulated system is just an obstructive factor, which complicates obtaining information relevant for macroscopic systems. However, a small volume might be an intrinsic property of real systems of interest, such as biological cells or small pores. Thus one would expect that the aggregation of peptides inside and outside biological cells, respectively, may be essentially different, being more pronounced in the latter case. The cytoplasm of cells contains a very high total concentration of proteins, nucleic acids, lipids, and supramolecular assemblies of these constituents. Taken together, these macromolecules occupy some 30% of the total cytoplasmic volume. Hence, a higher level of macromolecular crowding and an increasing role of surface effects are expected to make intracellular protein aggregation different from the extracellular one. The finite size of biological cells may be another factor, which can lead to distinct differences of intracellular and extracellular aggregation of peptides. This is an additional motivation for this study.

To study the effect of a finite system size on the aggregation of peptides, we chose aqueous solutions of amyloidogenic peptides, which are highly insoluble in water. Aggregation and subsequent amyloid formation is a central phenomenon in a number of diseases, such as Alzheimer's, Parkinson's, and type II Diabetes Mellitus, and seems to be the key factor in the development of the symptoms of these diseases (17). Upon formation of amyloid fibrils, the protein molecules adopt ordered, stacked cross-β-sheet structures (4,17–19). Numerous aspects of amyloid fibril formation remain unclear. Even in experimental studies in vitro, the factors, which facilitate or suppress formation of ordered peptide aggregates, are still little understood. In vivo, additional complications arise from the extensive presence of surfaces and from the possible confinement of peptides in small biological compartments, such as biological cells.

In this article, we study the effect of the system size and the effect of concentration on peptide aggregation in liquid water. Different methods, which allow the characterization of the degree of peptide aggregation, are proposed. We have found that peptide aggregation, as well as various properties of the peptide-water system, are highly sensitive to the system size and concentration, as expected for any phase transition. We discuss the possibility to account for these factors in simulation studies of aggregation phenomena in liquid water and the possible effect of the finite size of biological cells on the character of intracellular peptide aggregation.

SYSTEMS AND METHODS

Aqueous solutions of amyloidogenic fragments of the islet amyloid polypeptide IAPP (residues 15–19) were simulated at T = 330 K and P = 1 atm using Nosé-Hoover temperature coupling and Parrinello-Rahman pressure coupling. Molecular dynamics simulations were carried out with the GROMACS software package (20), with the TIP3P model for water and a modified AMBER force field (21) for the peptides. The N- and C-terminus of the peptide fragments were capped with acetyl- and methylamide-group, respectively. Periodic boundary conditions were applied and simulation runs were performed with 2-fs time steps. The number of peptides (N_p) in the simulation box varied from 1 to 56 and the number of water molecules (N_w) varied from ∼600–30,000. A total of 12 peptide-water systems were studied (see Table 1). The peptide weight concentration, C, is effectively equal to zero in the case of a single peptide in a simulation box, representing an infinite dilution, and varied from ∼2.5 to 42% in systems with N_p > 1. Accordingly, the lateral size, L, of the cubic simulation box was in the range of 2.7–9.9 nm. Initial configurations of these systems were prepared by random insertion of peptides in a cubic box with liquid water such that the shortest peptide-peptide distance exceeds some minimal value, which depends on concentration. Subsequently, water molecules overlapping with peptides were deleted. From 1 to 10 different initial configurations were used for different systems. Equilibration periods, estimated from the time evolution of various system parameters, varied from 10 to 25 ns, depending on the system size and peptide concentration (22). Configurations were saved every 2–5 ps and equilibration periods were excluded from the analysis.

TABLE 1.

Peptide-water systems studied

Np	Nw	C, %	L, nm	nr	ttot, ns	tpr, ns
1	591	5.81	2.69	10	300	250
3	1591	6.43	3.74	5	250	200
3	751	12.72	2.97	5	250	200
6	8600	2.48	6.50	5	100	75
6	3536	5.82	6.50	3	300	225
6	1480	12.87	3.73	3	600	525
6	626	25.89	2.93	3	300	225
12	6448	6.35	5.97	3	450	375
12	3079	12.72	4.75	6	660	570
12	1232	26.20	3.67	3	150	120
12	586	42.74	3.08	1	160	150
56	29,702	6.43	9.93	1	145	100

Parameters of the simulation systems studied: number of peptides N_p; number of water molecules N_w; peptide concentration C (weight percent); lateral box size L; number of independent simulation runs n^r; total simulation time t^tot; and total time of trajectories used in the analysis t^pr.

Analysis of peptide clustering was performed based on different criteria for the connectivity between two peptides (see below). One hydrophobic contact between two peptides exists, when a distance between two heavy atoms involved does not exceed the sum of their Van der Waals radii plus 2.8 Å. Clustering analysis allows distinguishing of the largest peptide cluster. We calculated the radius of gyration R_gyr of the largest peptide cluster, as well as its maximal extension L_max, measured as the maximal distance between two heavy atoms of peptides in the cluster. The secondary structure was determined using corresponding distributions of dihedral angles φ and ψ in the Ramachandran plot. A residue was considered as contributing to α-helices, when −110° ≤ φ ≤ −30° and −90° ≤ ψ ≤ −10°; to β-sheets, when −180° ≤ φ ≤ −100° and 60° ≤ ψ ≤ 180°; and to polyproline II structures, when −100° ≤ φ ≤ −30° and 60° ≤ ψ ≤ 180°. The solvent-accessible surface area of all peptides was obtained with a probe radius of 1.4 Å. Water molecules were considered as belonging to the hydration shell of the peptides, when the shortest distance between their oxygen atoms and the heavy atoms of the peptides does not exceed 4.5 Å. The peptide-peptide and peptide-water hydrogen bonds (H-bonds) were identified using the following criteria: an H-bond exists if the distance between donor and acceptor does not exceed 0.35 nm and if the donor-hydrogen-acceptor angle exceeds 120°.

Characterization of peptide aggregation

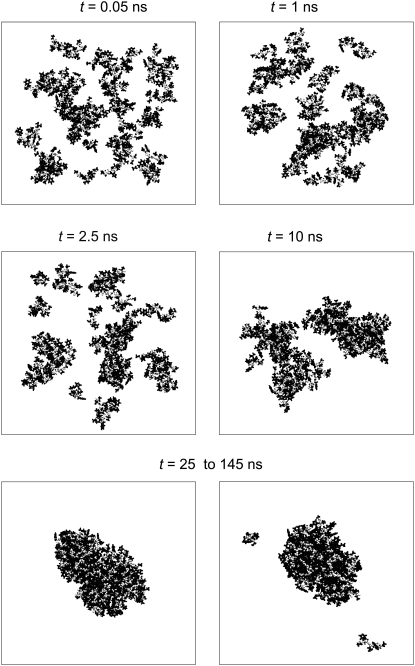
In the largest system studied (N_p = 56), the nucleation process can be seen at t < 25 ns (Fig. 1). Within 0.05 ns, initially randomly distributed peptides form well-distinguished clusters. These clusters grow and merge with time (see snapshots at t = 1 ns and at t = 2.5 ns) and two large droplets can be seen at t = 10 ns (Fig. 1). Finally, the nucleation process is completed and the system is equilibrated at t ≈ 25 ns. Due to the high peptide concentration used (C ≈ 6%) and the extremely low expected critical peptide concentration (C < 10⁻⁶), all peptides should belong to the organic-rich phase (peptide aggregate) almost permanently. However, the system shows two stable states, which interchange with time:

• State 1. All peptides are in one large cluster (lower-left panel in Fig. 1).

• State 2. Few peptides split from the large cluster (lower-right panel in Fig. 1).

This behavior is quite similar to that of finite Lennard-Jones fluids at constant density in the two-phase region (see Fig. 8 in Ref. (13)) or finite Ising magnets at constant magnetization in the two-phase region (see Fig. 3 in Ref. (16)). Only state 1 has an analogy with the macroscopic limit. State 2 is an artifact of the finite size of the simulation box and it does not exist in the macroscopic limit. It is to be noted that for the considered system with 56 peptides, an artificial state does not affect the system properties significantly, since the largest aggregate includes the vast majority of peptides permanently.

FIGURE 1.

Time evolution of peptide clustering in the system with N_p = 56 and C ≈ 6%. After the nucleation process (t < 25 ns), the system exhibits two stable states (lower panel): all peptides are in one cluster (left snapshot); and a few small clusters are separated from a larger peptide cluster (right snapshot). Backbones and side chains are shown in open and solid representation, respectively.

FIGURE 8.

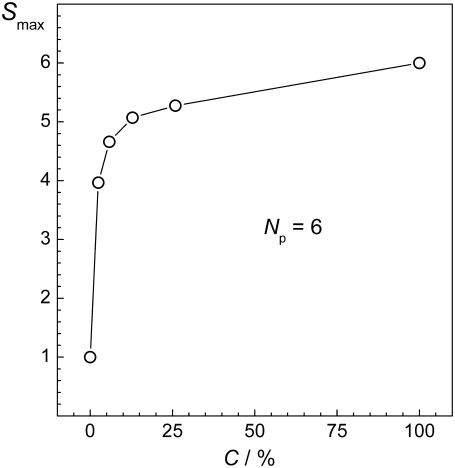
Dependence of the size S_max of the largest peptide cluster on the peptide concentration C at fixed peptide number N_p.

FIGURE 3.

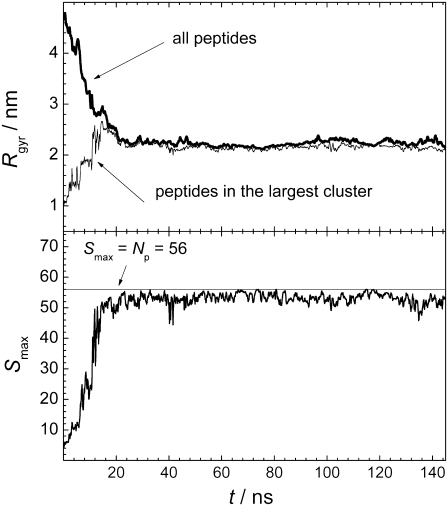
(Upper panel) Time evolution of the radius of gyration R_gyr of all peptides (thick line) and of peptides in the largest cluster (thin line). (Lower panel) Time evolution of the size S_max of the largest peptide cluster.

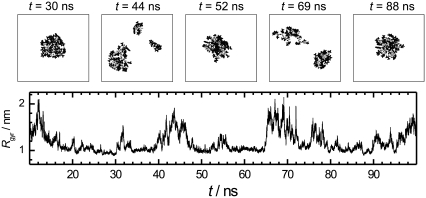
The existence probability of the artificial state and its effect on the system properties must increase with decreasing system size. The snapshots of peptides in the system with the same peptide concentration (C ≈ 6%), but with just six peptides, are shown in Fig. 2 at various time steps. In some instances, the peptides form a compact aggregate, whereas in other moments this aggregate splits into two or more parts. It is important to note that both states (with and without one compact aggregate) are stable. In this system, the artificial state without a compact peptide aggregate, strongly affects the system properties and makes them different from those expected in the macroscopic limit. Visual comparison of Figs. 1 and 2 reveals that the degree of peptide aggregation is significantly lower than that in the larger system. However, for a quantitative and systematic study of the effect of peptide concentration, system size, and other factors on peptide aggregation, some parameters reflecting the degree of their clustering (aggregation) should be introduced.

FIGURE 2.

Time evolution of peptide clustering in the system with N_p = 6 and C ≈ 6%. (Upper panels) Snapshots of peptides at various time steps, indicated in the figure. (Lower panel) Time evolution of the radius of gyration R_gyr of all peptides.

Radius of gyration of all peptides

Currently, the size of systems for atomistic computer simulations is limited to ∼10⁵ molecules. As the upper bound for the critical concentration of the hIAPP and its fragments is in low micromolar range (23,24), all peptides in the simulated system should belong to the organic-rich phase, and the water-rich phase of such a solution should be pure water. Therefore, the radius of gyration R_gyr of all peptides in the system, characterizing the compactness of the peptide arrangement, can be used as a measure of peptide aggregation (a similar approach was used in (25)). The applicability of such an approach is expected to worsen for more soluble peptides, as the presence of the peptide in the water-rich phase will increase R_gyr of all peptides, thus making the states “with aggregate” and “without aggregate” less distinguishable. Calculation of R_gyr of a system of particles requires the knowledge of the center of mass of this system. In the simulation box with periodic boundary conditions, this determination is not unique, as different choices of the origin of coordinate can give different locations of the center of mass, and, accordingly, different values of R_gyr. We have calculated the radius of gyration of the peptide system, placing the origin of coordinates on every peptide. The minimal value of R_gyr obtained by this procedure was taken as a measure of the compactness of the peptide system. The time evolution of R_gyr of all peptides in the system containing 56 peptides is shown in the upper panel of Fig. 3. As can be seen, R_gyr achieves steady values during an equilibration time of ∼25 ns, and further varies only within a relatively narrow range. This agrees with the visual inspection of the configurations of the peptides in the simulation box (Fig. 1).

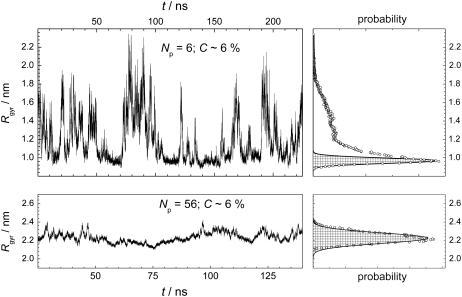
The time evolution of the radius of gyration R_gyr of all peptides for two systems of the same concentration (C ∼ 6%), but different sizes, are shown in the left panels of Fig. 4. The probability distribution P(R_gyr) was obtained by calculating the fraction of configurations, where the radius of gyration has the value R_gyr within some narrow interval. In the larger system, the distribution P(R_gyr) is highly symmetric and can be well fitted to a Gaussian function (dashed area in the lower-right panel in Fig. 4). In contrast, the probability distribution P(R_gyr) in the smaller system is highly asymmetric (upper-right panel in Fig. 4). The narrow peak of P(R_gyr) at ∼1 nm corresponds to the state, where all the peptides form a compact aggregate (see Fig. 2), whereas the wide tail of P(R_gyr) extending toward large R_gyr values corresponds to the state without a compact aggregate. To estimate the existence probabilities of these states, the distribution P(R_gyr) should be decomposed into two constituents. Taking into account that, in the larger system containing 56 peptides (lower panels in Fig. 4), the state with peptide aggregate dominates and the distribution P(R_gyr) can be well fitted to a Gaussian function, we can take an area under the Gaussian as an existence probability R₁ of the state with peptide aggregate. In the system with 56 peptides, the contribution to P(R_gyr) from the state in which the aggregate is partially dissolved (lower right snapshot in Fig. 1), is negligible, and R₁ = 1. In the smaller system with six peptides, the Gaussian contribution can be approximately estimated by fitting of the part of P(R_gyr) that includes its maximum and low R_gyr tail, by a Gaussian (see solid line in the upper right panel in Fig. 4). The existence probability of the state with the peptide aggregate in this system (determined from the dashed area) is markedly below 1 (R₁ = 0.34).

FIGURE 4.

(Left panels) Time evolution of the radius of gyration R_gyr of all peptides for two systems with the same peptide concentration, but different number of peptides. For system with N_p = 6, three time intervals of 75 ns, each from different simulation runs, are placed successively. (Right panels) Probability distribution of R_gyr for the dependences shown in the left panels (solid points). Fit of the probability distributions to Gaussian are shown by dashed areas.

The characterization of the degree of peptide aggregation by use of the distribution P(R_gyr) does not require any criterion for the connectivity between peptides. This is the main advantage of the proposed method, as the choice of an adequate connectivity criterion is not a trivial procedure (see below). On the other hand, this approach suffers from rather ambiguous extraction of the Gaussian contribution to the P(R_gyr). In particular, it is not applicable in very small systems (with N_p = 3 in our studies), where this contribution to the P(R_gyr) distribution is indistinguishable.

Clustering analysis: search for the connectivity criterion

A clustering analysis is the most basic approach for characterizing the arrangement of particles in the systems and is widely used in various fields of statistical physics. The system of particles may be described as an ensemble of clusters. Typically, the definition of clusters is based on some criterion for the connectivity between two particles. This criterion may be based on the interparticle distance, potential and relative kinetic energies of the two particles, the existence of H-bond, etc. The particular choice of the connectivity criterion depends on the problem considered. In the studies of the condensation phenomenon, two particles are usually considered as belonging to the same cluster, if the distance between them does not exceed a certain critical value r_crit, comparable to the distance between two particles in the condensed phase.

When considering the aggregation of amyloidogenic peptides, the condensed organic-rich phase appears as fibrillar aggregates. Therefore, the connectivity criterion should be related to the structure of fibrils. There are two characteristic interpeptide distances in fibrils: the interstrand distance between the neighboring peptides in the β-sheets is ∼0.5 nm and the intersheet distance is ∼1.0–1.1 nm (26). All peptides in the fibril belong to one cluster, if r_crit is close to the latter distance. Hence, in the clustering analysis of peptide aggregate formation in water, two peptides can be considered as belonging to the same cluster, if the distance between their centers of mass is <∼1.0–1.1 nm. Additionally, we can use a qualitatively different connectivity criterion, based on the number n_c of hydrophobic contacts between two peptides. However, typical values of n_c in fibrils are not known. The choice of the particular values of r_crit or n_c should satisfy well-established aspects of peptide aggregation. In particular, the degree of peptide aggregation must increase with increasing peptide concentration.

The clustering analysis allows one to distinguish the largest peptide cluster, which mimics an organic-rich phase of the studied system. Accordingly, various properties of the largest peptide cluster (shape, fractal dimension, density, etc.) can be studied. Additionally, the fraction f of the peptides in the largest cluster can be used as a parameter, reflecting the degree of aggregation.

Distance between the centers of mass

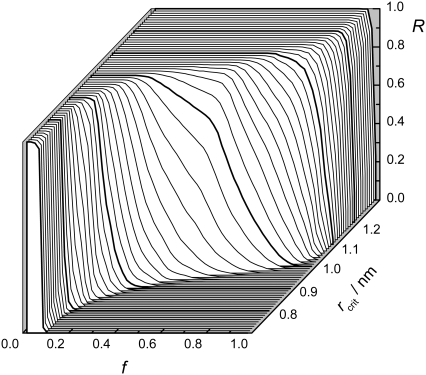
To choose the value r_crit for the distance between the center of mass of two peptides, which adequately characterizes peptide aggregation, we consider the largest system studied with N_p = 56. In this system, almost all peptides form one large aggregate permanently (see Fig. 1), hence, the existence probability R of the aggregate state is equal to 1. The dependence of the existence probability R to find at least fN_p peptides in the largest cluster of this system is shown for various choices of r_crit in Fig. 5. When r_crit < 0.9 nm, the fraction f of the peptides in the largest cluster never exceeds ∼0.2. This contradicts the visual observation and should be considered as unreasonable. When r_crit > 1.2 nm, the fraction f is always close to 1. At R = 1, a drastic increase of the fraction f occurs, when r_crit changes from 0.9 to 1.1 nm, in agreement with literature values of intersheet distances in fibrils (26). The presence of the majority of peptides (0.5 < f < 1.0) in the largest cluster can be considered as a signature of the state with peptide aggregate. Even in the largest system studied, f is never equal to 1, since a small fraction of peptides periodically splits from the main aggregate (see Fig. 1). Therefore, any values of f, which exceeds 0.5 and is not very close to 1, seems to be reasonable for the definition of the existence probability R of a state with peptide aggregate. In Ising magnets, a fraction of 2/3 of the excess magnetization forms a droplet at the transition point (15,16). Therefore, we use f = 2/3 for the definition of R.

FIGURE 5.

Probability R to find > fN_p peptides in the largest cluster at various choices of the distance r_crit between the center of mass of two peptides, used as a connectivity criterion.

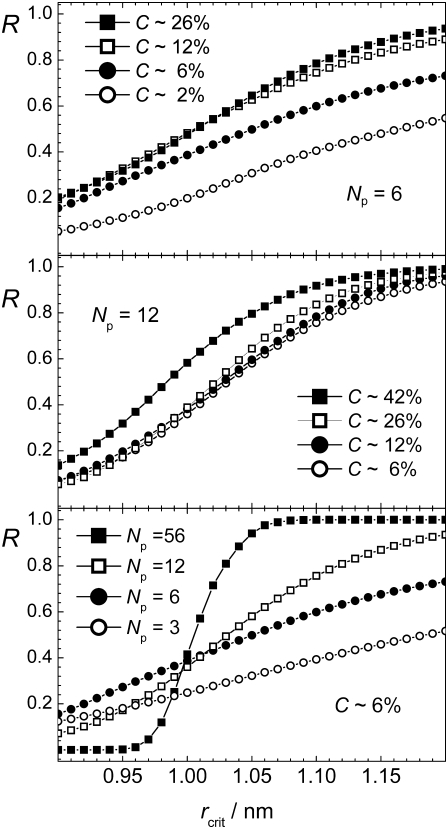
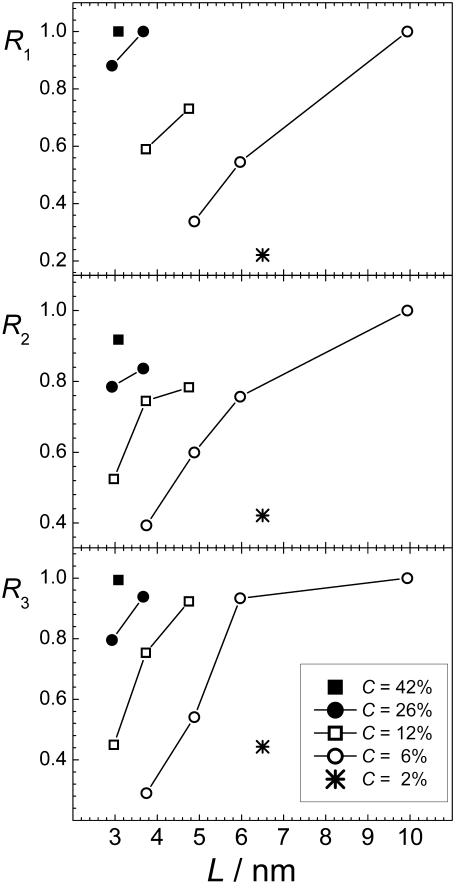
The dependence of the existence probability R defined in such a way on r_crit is shown in the upper and middle panels of Fig. 6 for systems with N_p = 6 and N_p = 12, respectively, and with several peptide concentrations C. As expected, R increases, when the connectivity criterion weakens, i.e., r_crit increases. A physically reasonable choice of the value r_crit should provide an increase of R with increasing peptide concentration at constant number of peptides. This condition is satisfied for r_crit > 1.0 nm, which may be considered as the lower limit for r_crit. The existence of such lower limit for r_crit is not expected for systems of simple isotropic molecules, and evidences a multilevel structural organization of the peptide aggregates. This can be seen, when the systems with approximately the same peptide concentration (C ≈ 6%) but different number of peptides are compared (lower panel in Fig. 6). When the connectivity criterion applied is stricter (r_crit < 1.0 nm), the systems with smaller peptide numbers N_p exhibit increased aggregation in comparison with larger systems. This is due to the fact that in the systems with just a few peptides, formation of a single β-sheet with interstrand distance of ∼0.5 nm is the main form of aggregation. In contrast, in larger systems, more than one β-sheet can be formed, and the use of r_crit < 1.0 nm artificially breaks the peptide aggregate into separate β-sheets even in the case of an ideal fibril. For the largest system studied with N_p = 56, the aggregation parameter R shows a pronounced sigmoidlike dependence on r_crit with an inflection point at ∼1.0 nm. Such sigmoidlike dependence, although less steep, is still seen in the system with N_p = 12, but it disappears in the systems with N_p = 6 and 3 (see lower panel in Fig. 6).

FIGURE 6.

Dependence of the degree of aggregation R (with f = 2/3) on the connectivity criterion r_crit, which is the distance between the center of mass of two peptides.

The choice of the connectivity criterion in studies of peptide aggregation should be meaningful also in the limit N_p → ∞, since simulation studies are typically aimed to reproduce the properties of macroscopic systems. Therefore, connectivity criteria with r_crit > 1.0 should be used, keeping in mind that their use overestimates peptide aggregation in small systems. In the largest system studied with N_p = 56, the state with peptide aggregate exists almost permanently and the probability R = 1, when r_crit exceeds 1.1 nm (see lower panel in Fig. 6). Below, we use the connectivity criterion r_crit = 1.1 nm for the distance between the centers of mass of two peptides and the minimal fraction f = 2/3 of peptides in the largest cluster to estimate the existence probability of the state with aggregate, denoted as aggregation parameter R₂.

Number of hydrophobic contacts

The connectivity criterion based on the distance between the centers of mass does not account for specific interpeptide interactions such as interpeptide H-bonds or direct contact of the atomic groups of two peptides. For the description of formation of ordered peptide aggregates, the connectivity criteria which deal with specific interpeptide interactions may be important. As a first step in this direction, we have also analyzed the peptide aggregation using the number n_c of hydrophobic contacts between two peptides as a connectivity criterion.

The dependences of the existence probability R (with f = 2/3) on the decreasing number n_c in various systems (not shown) are quite similar to those in Fig. 6. With decreasing number n_c, the probability R approaches 1, as expected. The physically justified enhancement of aggregation with increasing peptide concentration is observed, when n_c ≤ 10. On the other hand, in the system with N_p = 56, the requirement R = 1 is satisfied for n_c ≤ 15. Therefore, below, we use 10 hydrophobic contacts between two peptides as a connectivity criterion and the corresponding existence probability of the state with aggregate is denoted as aggregation parameter R₃.

Effect of concentration and system size on the degree of peptide aggregation

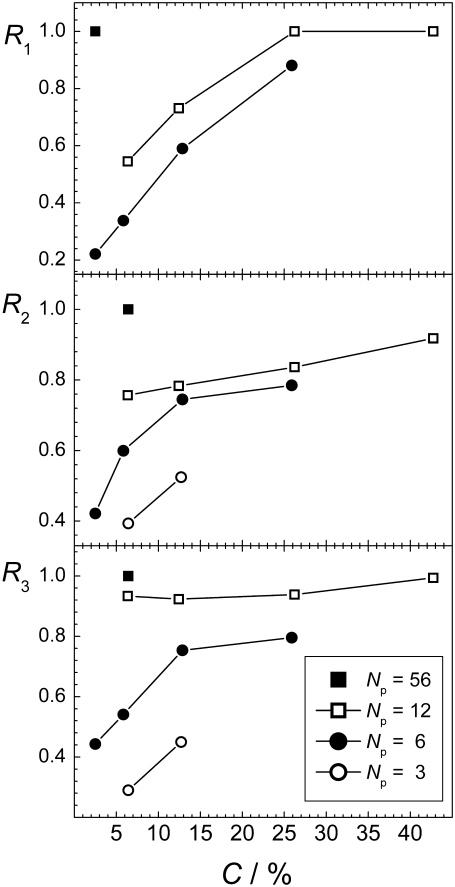
The dependences of the aggregation parameters R₁, R₂, and R₃ on peptide concentration C are shown in Fig. 7. All three aggregation parameters used show a qualitatively similar behavior: the aggregation is fostered with increasing C, when the number of peptides is fixed. Although such dependence was, in fact, imposed by the choice of the connectivity criteria for parameters R₂ and R₃, this is not the case for the aggregation parameter R₁, which characterizes the degree of aggregation without imposing some connectivity criterion. Enhancement of aggregation with increasing peptide concentration is physically obvious and we are not aware of any mechanism, which can decrease the aggregation propensity when the number of peptide is fixed but the amount of solvent decreases. Such behavior is physically obvious, but it did not get proper attention in the simulation studies of the aggregation of peptides or other particles in liquid water. The effect of concentration on peptide aggregation is illustrated by the dependence of the size S_max of the largest peptide cluster on C for the systems with N_p = 6, shown in Fig. 8. Obviously, S_max = 1 upon infinite dilution (C = 0%) and S_max = 6 in the absence of solvent (C = 100%). The steepness of the dependence S_max(C) is determined by the degree of the solubility of the peptides considered. For more soluble peptides, we may expect a more gradual increase of S_max with C.

FIGURE 7.

Dependence of the aggregation parameters R₁, R₂, and R₃ (upper, middle, and lower panel, respectively) on the peptide concentration C at fixed numbers of peptides, indicated in the figure.

The data shown in Fig. 7 are clear evidence that the degree of aggregation increases strongly when the concentration is fixed but the number of peptides in the system increases. This is shown explicitly in Fig. 9, where the aggregation parameters R₁, R₂, and R₃ are given as a function of the box size L. All three different aggregation parameters depend on the system size in a drastic way. In fact, the effect of system size on aggregation (Fig. 9) is as strong as the effect of peptide concentration (Fig. 7). A decreasing system size has the same effect as a decreasing peptide concentration: peptides become, apparently, more dissolved in water. The physical origin of this phenomenon is the effect of the finite system size on the minority phase in the two-phase region. The same behavior is seen in simple fluid and magnet systems, being at constant density or magnetization, respectively (11–16). Hence, any attempts to extract information relevant for macroscopic (infinite) water-peptide systems from simulations, should take into account the drastic effect of the finite system size on peptide aggregation.

FIGURE 9.

Dependence of the aggregation parameters R₁, R₂, and R₃ (upper, middle, and lower panel, respectively) on the system size L at fixed peptide concentrations (indicated in the figure).

Effect of concentration and system size on various system properties

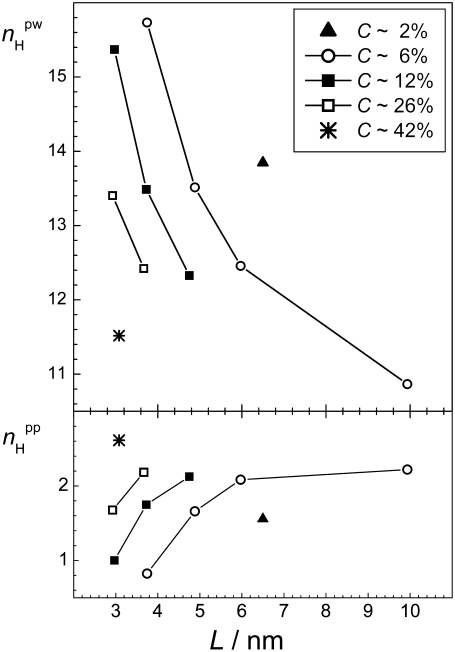
Because the concentration and the system size strongly affect the degree of peptide aggregation as measured by different parameters, various properties of the peptide-water system considered should also be strongly sensitive to these two factors. The dependence of the average number of interpeptide H-bonds per one peptide (i.e., 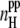) on the system size is shown in the lower panel of Fig. 10 for various peptide concentrations. These dependences are qualitatively similar to those of the aggregation parameters shown in Fig. 9, i.e., 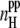increases with increasing concentration C and with increasing system size L. The average number of peptide-water H-bonds (i.e., 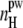) is also strongly sensitive to C and L, although this dependence is opposite to that of 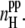The clear correlation between the aggregation parameters and other properties of the peptide-water system evidences the reasonable choice of the aggregation parameters.

FIGURE 10.

Dependence of the average number 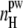of peptide-water (upper panel) and the average number 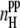peptide-peptide (lower panel) H-bonds on the system size L at several fixed peptide concentrations.

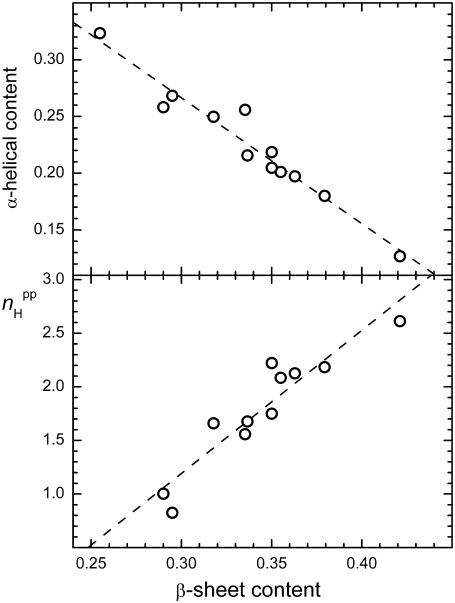
The secondary structure content of peptides is an important property, which is used in the characterization of peptide aggregation both in simulations and experiments. We have found that the β-sheet and α-helical contents are strongly sensitive to the system size and concentration, and vary from 0.28 to 0.42 and from 0.11 to 0.33, respectively. Nevertheless, there is a clear anticorrelation between the α-helical and β-sheet contents of the peptide-water system (see upper panel in Fig. 11). In turn, the β-sheet content is proportional to the average number 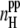of interpeptide H-bonds per one peptide (see lower panel in Fig. 11).

FIGURE 11.

Correlation between β-sheet content and the average number 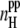of peptide-peptide H-bonds (lower panel) and correlation between β-sheet content and α-helical content (upper panel) in all studied systems.

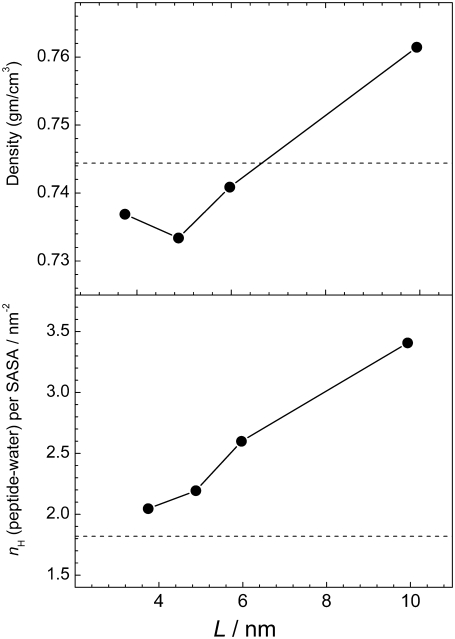
Important information about the driving forces of peptide aggregation can be obtained from the analysis of the properties of hydration water. The water-mediated attraction between hydrophobic groups of peptides as well as Coulombic and H-bonding interactions between peptides are the main driving forces of peptide aggregation. An analysis of the effective hydrophobicity/hydrophilicity of the surface of peptide aggregates may give insight into the mechanism of aggregation. If the peptide surface exposed to water becomes more hydrophilic upon aggregation, the attraction between hydrophobic groups may be considered as the main driving force in aggregation. Otherwise, aggregation should be attributed mainly to the interpeptide Coulombic and H-bonding interactions. The strength of water-peptide interaction can be characterized by the number 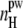of water-peptide H-bonds per unit area of the solvent-accessible surface. The dependence of this number on the system size L at peptide concentration C ≈ 6% is shown in the lower panel of Fig. 12, where the value for a single peptide is shown by a horizontal line. With increasing system size (and, accordingly, with increasing aggregation), the surface of peptides exposed to water becomes more hydrophilic. We may conclude that the hydrophilicity of the peptide surface exposed to water enhances upon aggregation and the hydrophobic attraction between hydrophobic groups of the peptides studied is a main driving force of their aggregation. This should be attributed to the presence of hydrophobic caps at the peptide ends.

FIGURE 12.

Dependence of the average number 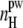of peptide-water H-bonds normalized by the peptide solvent-accessible surface area on the system size L (lower panel) and dependence of the average density ρ_h of hydration water (upper panel) on the system size L at peptide concentration C ≈ 6%.

The density ρ_h of water in the hydration shell of peptides can also be used as a measure of the effective strength of a peptide-water interaction: more hydrophobic surfaces cause a decrease of the density of hydration water. The density ρ_h of hydration water can be simply estimated, if the solvent-accessible peptide surface as well as the number of water molecules in the shell of some width near the surface is known. The dependence of the density ρ_h of hydration water on the system size L at peptide concentration C ≈ 6% is shown in the upper panel of Fig. 12. The trend toward more dense hydration water upon aggregation is clearly seen, which corroborates our conclusion about the leading role of hydrophobic attraction in aggregation of the IAPP fragments, as derived from the analysis of water-peptide H-bonding (see lower panel in Fig. 12).

Properties of the largest peptide cluster

A clustering analysis provides the possibility to explore various properties of the largest peptide cluster, which can be considered as an embrion of organic-rich fibrillar phase. The time evolution of the size S_max of the largest peptide cluster (lower panel in Fig. 3) as well as the time evolution of its radius of gyration R_gyr (upper panel in Fig. 3) can be used to characterize the equilibration process. Similar to the radius of gyration R_gyr of all peptides, the properties of the largest peptide cluster achieve saturation in ∼25 ns. Note that the R_gyr of all peptides and of the peptides in the largest cluster are very close due to the strong degree of aggregation in the largest system studied (upper panel in Fig. 3).

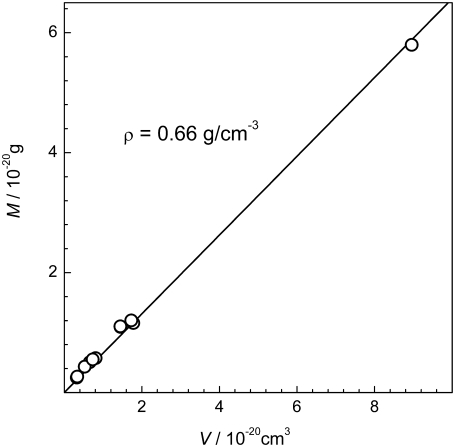
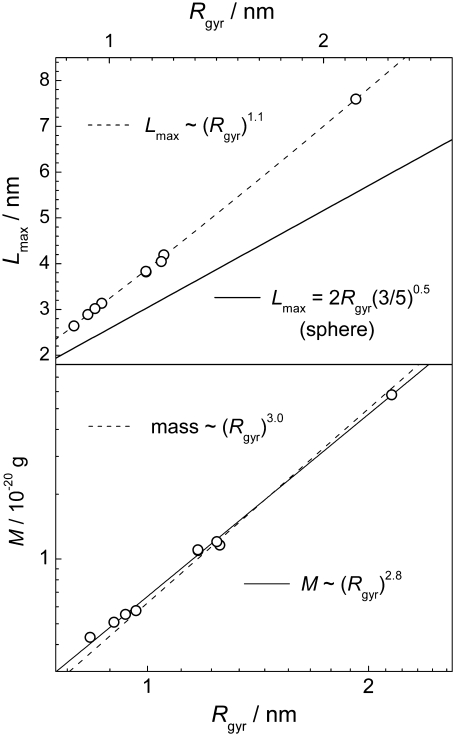
The structural properties of the largest peptide cluster may be characterized by the relation between its average mass M and volume V. In a first approximation, V can be estimated from the radius of gyration R_gyr of the largest peptide cluster, assuming that it is a spherical body: V = (4/3)π 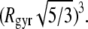The obtained dependence M(V) in the various systems is shown in Fig. 13. If the peptide cluster is a three-dimensional object, its density is equal to the slope of the dependence M(V), which is ρ = 0.66 g/cm³. Since a spherical shape of the peptide cluster was imposed, the estimation given above is a lower limit for the aggregate density, as the sphere provides the maximal volume at fixed radius of gyration. Information about the shape of the largest cluster can be obtained from the analysis of the maximal extension L_max of the largest cluster. The dependence of the average value of L_max on the average value of R_gyr in the various systems is shown in the upper panel of Fig. 14. For comparison, the dependence expected for spherical object, whose 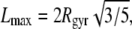is also shown. The dependence L_max(R_gyr) for the peptide cluster deviates from that expected for spherical objects, indicating an elongated shape of the peptide clusters.

FIGURE 13.

Dependence of the average mass M of the largest peptide cluster, in various systems, on its volume estimated as the volume of a sphere with the corresponding radius of gyration (circles). The upper limit for the density of the largest peptide cluster is estimated from the slope of the linear fit (solid line).

FIGURE 14.

(Upper panel) Dependence of the maximal extension L_max of the largest peptide cluster on its radius of gyration R_gyr in various systems. (Lower panel) Dependence of the mass M of the largest peptide cluster on its radius of gyration R_gyr in the double logarithmic scale.

To look into more detail in the mass distribution within the largest cluster, we plot the dependence of M on the radius of gyration R_gyr in a double logarithmic scale (lower panel in Fig. 14). The slope of this dependence is equal to the fractal dimensionality of the object. The fit of the dependence M(R_gyr), shown in the lower panel in Fig. 14, to a power law yields the fractal dimension of the largest peptide cluster equal to 2.8 (solid line), which notably differs from 3 (dashed line), corresponding to compact three-dimensional objects. A fractal-like structure of the peptide aggregate is also supported by the dependence L_max(R_gyr), which is not linear, but is L_max ∼ 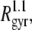indicating that the fractal dimension of the peptide clusters is <3. In fact, the fractal dimensionality of proteins is always <3 (27) and, therefore, a low fractal dimension of peptide clusters is not surprising.

DISCUSSION

The results of the simulation studies presented have two main implications. The first implication is related to the necessity of taking into account the finite size of the simulated system, when one intends to reproduce the properties of the real macroscopic system. The second implication is related to natural systems, where the finite system size is an intrinsic property.

Finite system size in silico: simulation studies of binary systems

Generally, the simulation studies are aimed at reproducing the properties of macroscopic systems. There are various factors that complicate the realization of this goal, and it is important to know to what extent these factors make the properties of the simulated system different from those of its macroscopic analog. For example, the ability of the available force fields to reproduce various system properties is approximative even for simple fluids and their mixtures. Another complication arises from the necessity to correctly reproduce the phase behavior of interacting particles, which requires application of sophisticated simulation methods (such as Monte Carlo simulations in the grand canonical ensemble). Finite system size is yet another problem which accompanies any simulation study designed to reproduce the properties of macroscopic systems.

The effect of a finite system size on its properties is well known in statistical and computational physics. Finite size scaling allows approaching the properties of the macroscopic system. This can be achieved by simulations of several systems of different sizes (measured, for example, by their linear extensions L) with subsequent extrapolation of the results to the macroscopic limit L → ∞. The effect of the finite size depends on the thermodynamic state of the system. For example, it is especially strong in the vicinity of the critical point due to the suppression of the fluctuations by the finite system size. On the other hand, when the system is in a thermodynamic state, that is distant from the phase transition, the system properties are not so strongly affected by its finite size.

Typically, simulation studies of aqueous solutions are performed in constant-volume or constant-pressure ensembles. As an aqueous solution is a mixture, the concentration of solutes is a key parameter of such system, which is also kept constant. Simulations of a single solute in water can be used for reproducing the properties of the macroscopic system only at infinite dilution. In this case, the finite size does not affect the system properties noticeably when the box size essentially exceeds the size of a solute. Addition of just a second solute to the system changes the status of simulations in a drastic way. Now the clustering (aggregation) of solutes is possible and strongly depends on the concentration of the solutes and the thermodynamic state of the system (28–30). If this state is distant from the demixing phase transition, the probability to find a cluster containing S molecules drops in a drastic way with increasing S and the vast majority of solute molecules exists as monomers or belongs to small clusters. Of course, the finite system with just a few solutes fails to reproduce the cluster size distribution of a macroscopic system. However, this affects mainly the large clusters. The small clusters containing the majority of the solute molecules are not strongly perturbed.

The distorting effect of the finite size on the system properties becomes enormous as the system enters the two-phase region (11–16). This situation is typically encountered in the simulation studies of the strongly aggregating solutes in liquid water, which are usually performed in one simulation box with the solute concentration deeply inside the two-phase region. However, the effect of a finite system size is generally neglected not only in biosimulations, but also in simulation studies of simple small hydrophobic solutes in liquid water (see, for example, (31–33)). Moreover, the effect of concentration on the aggregation of solute molecules was considered in only a few studies (34,35). In large enough systems, the solution may separate into two coexisting phases with an explicit interface between them. However, this is not the case in the majority of simulation studies of solute aggregation in water, where the number of solutes is usually small. The finite system size suppresses the minority (organic-rich) phase and produces an artificial stable state of the system in which the organic-rich phase is dissolved. The existence probability of this state increases with decreasing system size and with decreasing solute concentration (within the two-phase region). To make the simulation studies of such systems relevant to the real systems, it is necessary to consider the type of phase transition and the character of the coexisting phases, and to perform a correct extrapolation of the simulation results to the macroscopic limit.

Finite system size in silico: simulation studies of peptide aggregation

In the case of amyloidogenic peptides in water, the organic-rich phase appears as a solidlike ordered aggregate. Typically, the organic-rich phase is a minority phase and its properties are strongly affected by the finite system size. When the peptide concentration exceeds the critical one, the peptides should form highly ordered fibrils in the macroscopic limit. However, the number of peptides is relatively small in the simulations. Just a few peptides in the simulation box can only to some extent exhibit properties of the peptide aggregate expected in the macroscopic limit. Therefore, the simulation studies of the aqueous solutions of peptides must include the analysis of the effect of the system size on the degree of aggregation and all other system properties, and the artificial system properties, produced solely by the finite size effect, should be excluded from the consideration. In a finite system of aqueous solution of peptides whose concentration is within the two-phase region, there are two stable (equilibrium) states. One state is that with the peptide aggregate, which represents an organic-rich phase. Of course, this phase, reproduced by just a few peptides, differs strongly from the ordered peptide aggregate seen in macroscopic systems. However, this state will evolve toward its analog in the macroscopic limit upon increasing the system size (number of peptides in the simulation box at fixed concentration). In the other state, the organic-rich phase is dissolved, either partially or completely. This state is a pure artifact of the finite system size and has no analog in the macroscopic limit, as it disappears with increasing system size. The time intervals of the molecular dynamics trajectory, where the system exists in such an artificial state, can be determined using, for example, the time evolution of the total radius of gyration of all peptides (see Fig. 2). Exclusion of these time intervals from the analysis should help to approach the properties of the macroscopic system. Note that an equilibrium between the previously mentioned states was observed in simulation studies of three amyloidogenic peptides in implicit water (25), although the origin of such behavior was not discussed.

The most important finding of our studies is a drastic effect of the system size on peptide aggregation. This effect seems to be responsible for the instability of aggregates consisting from just a few peptides, as seen in simulations (36–38). This effect of a finite size of a system, which is in the two-phase state, is known and well understood for Ising magnets and Lennard-Jones fluid, but was not studied before in more complex systems. To the best of our knowledge, this is the first study showing the manifestation of this effect in binary mixtures. The complex peptide-water systems with low solubility of the peptide were chosen due to the importance of simulation studies of the aggregation of biomolecules in water. Our simulation studies of the peptide aggregation with various peptide concentrations clearly show that the concentration affects all system properties in a drastic way. This effect is well understood and seems to be obvious. The degree of peptide aggregation (Fig. 7), H-bonding (Fig. 10), secondary structure content and other system properties strongly depend on peptide concentration. The dependence of the size of the largest peptide cluster on concentration at fixed peptide number (Fig. 8) nicely illustrates the necessity to account for the concentration effect in the simulation studies of aggregation phenomena. This effect is unavoidable, when the number of aggregating particles exceeds 1. In particular, any properties of the system with just two aggregating particles are concentration-dependent.

When studying the effect of concentration and system size on aggregation, it is important to introduce an adequate parameter characterizing the degree of aggregation. Although the use of the radius of gyration of all peptides for this purpose (Figs. 2–4) does not require a criterion for connectivity between peptides, it does not allow obtaining the cluster size distribution and an analysis of the properties of the largest peptide cluster. A more detailed analysis of aggregation requires the introduction of a connectivity criterion between two peptides. Such choice is not unambiguous even for simple molecules and is more difficult for biomolecules. In a first approximation, we have used the distance between the center of mass of two peptides as a measure of the connectivity. The disadvantage of this measure is the inability to distinguish the ordered character of the peptide aggregate. Clearly, the search for more adequate connectivity criteria in the studies of the formation of ordered peptide aggregates is necessary. These criteria should be derived based on the structure of the macroscopic ordered peptide aggregates (fibrils) and include the interatomic distances between two peptides and the H-bonds in particular. Note, that the effect of the finite system size on the ordered character of the peptide aggregate is unknown. We may assume that the more ordered aggregate will be more affected by this effect. However, this assumption should be tested in simulations.

Finite system size in vivo: aggregation of proteins in cells

The effect of the system size on peptide aggregation complicates the attempts to reproduce the properties of macroscopic systems by simulations of finite systems. However, this is an intrinsic property of the finite system. So, if the real system of interest is not macroscopic and contains a relatively small number of peptides, their aggregation will be suppressed by the finite system size as well. This situation may be relevant for the case of peptides in small volumes, such as biological cells or their compartments. In vivo, amyloidogenic peptides can be found both in intracellular and extracellular fluids and these two pools of peptides often seem to be mutually related (39,40). The extracellular fluid may be regarded as an essentially macroscopic system and formation of the peptide-rich phase via the phase transition should largely follow the regularities normally encountered in the in vitro experiments with bulk aqueous solutions of the amyloidogenic peptides. The picomolar concentrations of the islet amyloid polypeptide in the plasma (41) and of the Aβ protein in the cerebrospinal fluid (42,43) should be considered as critical for their aggregation, because the extracellular fluid is in direct contact with amyloid plaques. The production of amyloidogenic peptides in cells and their accumulation with time (39,44,45) evidence that the intracellular concentration noticeably exceeds the critical one. The absence (or at least slowing down) of extensive fibrillation in cells might be due to the effect of the relatively small volume of cells or their compartments. Due to the high insolubility of amyloidogenic peptides, the presence of dozens or hundreds of peptides in a cell may already provide conditions of strong oversaturation. Hence, a small cell volume should suppress peptide aggregation in general and formation of ordered aggregates, in particular. The escape of these peptides to the extracellular fluid (for example, due to the destruction of the cell membrane upon its death), makes fibrillation unavoidable at the same peptide concentration. If the oversaturation is not too strong, the lag time of fibril formation may still take many years.

The suppression of aggregation by a small system size has a general physical origin and, therefore, is unavoidable. However, it is rather difficult to estimate the magnitude of this effect, which depends on the system and detailed solution conditions considered. Additionally, other factors (first of all, surface effects) may be equally or even more important. We may expect that peptide adsorption on some surfaces is favorable for the ordered character of their aggregation, whereas confinement in a small volume should suppress formation of the ordered aggregates. Further studies are necessary to clarify those cases where the finite size of biological cells noticeably affects intracellular peptide aggregation.