Mechanical Stability of Helical β-Peptides and a Comparison of Explicit and Implicit Solvent Models

Abstract

Synthetic β-peptide oligomers have been shown to form stable folded structures analogous to those encountered in naturally occurring proteins. Literature studies have speculated that the conformational stability of β-peptides is greater than that of α-peptides. Direct measurements of that stability, however, are not available. Molecular simulations are used in this work to quantify the mechanical stability of four helical β-peptides. This is achieved by subjecting the molecules to tension. The potential of mean force associated with the resulting unfolding process is determined using both an implicit and an explicit solvent model. It is found that all four molecules exhibit a highly stable helical structure. It is also found that the energetic contributions to the potential of mean force do not change appreciably when the molecules are stretched in explicit water. In contrast, the entropic contributions decrease significantly. As the peptides unfold, a loss of intramolecular energy is compensated by the formation of additional water-peptide hydrogen bonds. These entropic effects lead in some cases to a loss of stability upon cooling the peptides, a phenomenon akin to the cold denaturing of some proteins. While the location of the free energy minimum and the structural helicity of the peptides are comparable in the implicit-solvent and explicit-water cases, it is found that, in general, the helical structure of the molecules is more stable in the implicit solvent model than in explicit water.

INTRODUCTION

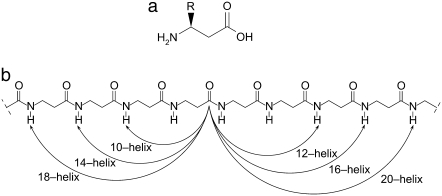
One of the aims of structural biology is the prediction of secondary and tertiary structure of proteins from knowledge of their sequence. Considerable efforts have been made to ascertain the principles of protein folding and to conceive strategies for design of specific folded structures. An attractive approach has emerged that makes use of synthetic β-peptides to identify some of these basic principles. Naturally occurring proteins can be viewed as polymers made of α-amino acids; likewise, synthetic β-peptides are polymers made of β-amino acids. The basic structure of a β-peptide is shown in Fig. 1 (1). It is generally perceived that β-peptides are more conformationally stable than α-peptides, particularly when cyclic residues are used to constrain the backbone dihedral angles. (2) They can form multiple types of helices (1,3), sheets (4,5), and hairpin turns (6). The experimental literature on helical β-peptides is relatively limited (7–25). Emerging applications indicate that β-peptides exhibit antimicrobial and antifungal characteristics (13,16,19,26,27). Recent work has also shown that β-peptides exhibit an intriguing propensity to self-assemble, as indicated by the formation of liquid crystalline phases (21), the formation of quaternary structures (22,24), and the formation of ordered structures on gold surfaces (25).

FIGURE 1.

(a) Structure of β³-amino acids which are the monomer for β-peptides considered in this work. (b) The β-peptides from this work can form a variety of secondary structures. Some of the possible helices for β-peptides are shown using the backbone structure. The helix is named by the number of atoms between the hydrogen bond. For example, a 14-helix has 14 atoms between N–H and C=O.

Past theoretical or computational studies of β-peptides have been largely limited to structural analysis of various molecules in a variety of solvents. In recent work, we have examined the mechanical stability of several β-peptides by subjecting them to pulling, i.e., unfolding forces (2). While that study revealed that β-peptides are indeed remarkably stable, it also raised intriguing questions regarding the role of electrostatic and hydrogen-bonding interactions on the overall behavior of these molecules. More specifically, our past simulations were carried out with electrically neutral molecules immersed in an implicit, dielectric continuum (2). Experiments suggest that hydrophobic interactions play an important role on the folded structure and conformational stability of β-peptides (28,29). It is therefore of interest to determine to what extent an implicit-solvent model can capture the hydrophobic forces that arise in such systems, and to explore whether our explicit model can provide new insights into the folding of β-peptides.

Many of the applications envisaged for β-peptides rely on specific secondary structures and their stability. Force spectroscopy provides a useful means to study the strength of proteins in resisting destabilizing forces. Atomic force microscopy or optical tweezers can be used to determine the response of proteins to mechanical strain (30,31). This response is important for proteins that form the cellular matrix, such as titin (32,33), but could also prove to be an effective means to study structure-property relations in β-peptides. Force spectroscopy could also prove valuable in refining the force fields required for accurate simulations of β-peptides. In previous studies of β-peptides a variety of force fields have been used and, in most cases (including our work), α-peptide parameters have simply been extended to β-peptides. While most of the previous work has generally been successful in describing a number of experimentally observed features, the validity of α-peptide parameters for β-peptide simulations remains to be assessed. Also note that, because force spectroscopy only provides data on a pulling force as a function of stretching, molecular simulations would help interpret experimental measurements by providing a precise emulation of a deformation experiment with atomic-level resolution (31).

Theoretical studies of β-peptides in explicit water have been limited. Günther and Hofmann (34), Möhle et al. (35), and Günther et al. (36) used ab initio calculations and molecular dynamics simulations with the CHARMm 23.1 force field to determine the propensity of β-amino acids to adopt different conformations in a continuum solvent. Using the OPLS-AA force field, Kritzer et al. (28) and Chandrasekhar et al. (37) used energy-minimization to ascertain which side chains are more likely to promote stabilization of the 14-helix in β-peptides. These authors used an implicit solvent model (Generalized Born “GB/SA”) to account for solvation effects. In a series of articles, the group of van Gunsteren and co-workers (38–44) examined the conformational stability of a variety of β-peptides in methanol using the GROMOS force field. In one study, this group also compared the structure of a particular β-peptide in explicit methanol to that observed in explicit water (23). By studying the configurational entropy of β-peptides, they concluded that the solvent degrees of freedom were critical for accurate description of the relative stability of the folded over the unfolded states (40,41). Hentényi et al. (17) and Martinek et al. (45) used molecular mechanics and ab initio calculations in vacuum to examine the conformations adopted by cyclic-residue containing β-peptides, and found that cyclohexane groups stabilize the 14-helix. To the best of our knowledge, our group has been the only one to examine the mechanical stability of helical β-peptides in a systematic manner (2). Our simulations revealed that torsional constraints and electrostatic interactions are important contributors to the resistance of β-peptides to undergo deformation. While our original study did include a brief analysis of stability in explicit water and methanol, all of our deformation calculations were conducted using an implicit solvent model. There is a scarcity of studies pertaining to the stability of water-soluble β-peptides in more realistic, explicit-water models.

In this work we present results of simulations of the deformation of several helical β-peptides in explicit water. Our work is primarily motivated by a need to understand the role of hydrogen-bonding interactions on the stability of β-peptides. Aware of the limitations of implicit solvent models, we seek to understand the differences that arise when using implicit versus explicit solvent models. We turn to the mechanical stability of β-peptides for direct comparison of simulations in implicit and explicit solvent; the opportunity to compare these results to atomic-force microscopy experiments that are now underway in our laboratory makes mechanical stability a particularly interesting property to consider. More specifically, we compare the mechanical stability of four different helical β-peptides in TIP3P water (46) to that observed in a distance-dependent dielectric implicit solvent model (47). A distance-dependent dielectric environment makes use of a linear or nonlinear function (48,49) to represent the solvent screening. Linear dielectric functions are easy to implement and computationally inexpensive compared to more demanding implicit solvent models. Previous work has shown that the distance-dependent dielectric model can strengthen electrostatic interactions such as salt bridges (49). Neutralized side chains can be used to alleviate this effect (49). The four molecules considered in our simulations include different combinations and arrangements of hydrophilic and hydrophobic groups. Their mechanical stability is assessed by calculating the change in free energy (or potential of mean force) associated with the forced unfolding (or pulling) of the molecules. For all four β-peptides, we compare the enthalpic and entropic contributions to the free energy, and analyze the role of solvent in determining the peptides' conformational stability. Our results indicate that, consistent with past experimental and theoretical work, helical, cyclic-residue containing β-peptides are highly conformationally stable. However, our results reveal that, depending on the sequence of the β-peptide, that conformational and mechanical stability can have completely different origins. In some cases it can be attributed to solvent-mediated entropic interactions, and in some others it is due to intramolecular enthalpic interactions.

METHODS

Molecular model

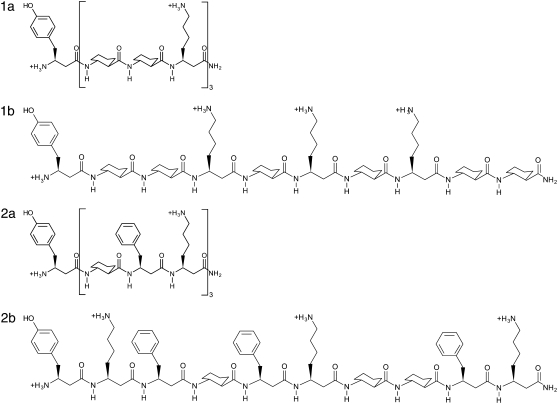
To examine the effects of solvent models on β-peptide mechanical stability we examine four peptides with different amino acid residues. The four peptides considered in this work are given in Fig. 2 and have the chemical formulas:

• 1a: (β³-hTyr)-[ACHC-ACHC-(β³-hLys)]₃;

• 1b:(β³-hTyr)-[ACHC-ACHC-(β³-hLys)]-[ACHC-(β³-hLys)-ACHC]-[(β³-hLys)-ACHC-ACHC];

• 2a: (β³-hTyr)-[ACHC-(β³-hPhe)-(β³-hLys)]₃;

• 2b: (β³-hTyr)-[(β³-hLys)-(β³-hPhe)-ACHC]-[(β³-hPhe)-(β³-hLys)-ACHC]-[ACHC-(β³-hPhe)-(β³-hLys)].

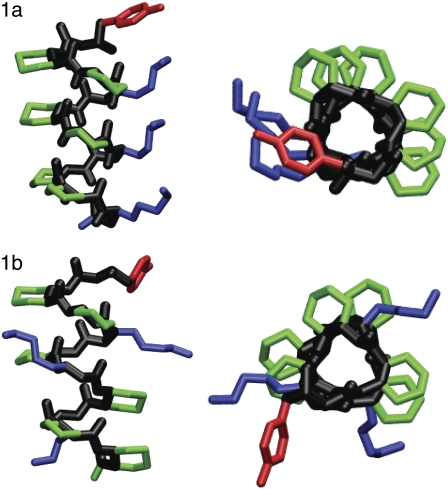
All of the peptides contain at least one cyclic residue, trans-2 aminocyclohexanecarboxylic acid (ACHC), which has been shown to stabilize the so-called 14-helix conformation (7). The 14-helix is named for the 14-membered ring between hydrogen-bonded atoms C = O_i and H-N_i-2 (see Fig. 1). It exhibits three residues per turn, a property that results in a structure with three distinct faces as seen in Fig. 3 for peptides 1a and 1b. Molecule 1 contains two ACHC residues and one β³-homolysine per turn. Because of the arrangement of the side chains in the 14-helix, in isomer 1a the β³-homolysine residues are displayed on one face of the helix. We also consider the isomer 1b, which displays one β³-homolysine residue on each face of the helix. Molecule 2 contains one ACHC cyclic residue, one hydrophobic β³-homophenylalanine residue, and one β³-homolysine residue per turn. The isomer 2a has all the β³-homolysine residues on one face, while isomer 2b has each β³-homolysine residue on a different face of the helix.

FIGURE 2.

Structures of four β-peptides used in this work, 1a, 1b, 2a, and 2b, in their charged state.

FIGURE 3.

Stick representations of β-peptides 1a and 1b considered in this work. The figures are colored with the backbone in black, the cyclic residues in green, the β³-homolysine residues in blue, the β³-homotyrosine residue in red, and the β³-homophenyalanine residues in red. For clarity, hydrogens have been removed. On the left is a side view and representation on the right is shown looking down the helical axis. These figures were made using VMD (77).

The CHARMm27 (50,51) all-atom force field was used to model our β-peptides. For a complete description of the parameters employed in our work, readers are referred to our previous simulations with β-peptides (2).

The potential energy function employed in this work is of the form

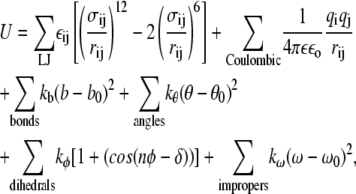(1)

where r_ij is the distance between site i and j, ε_ij is the Lennard-Jones well depth, σ_ij is the position of the minimum in the Lennard-Jones potential, q_i is the charge of site i, ε is the dielectric constant, ε_o is the vacuum permittivity, k_b is the bond force constant, b is the bond length, b₀ is the location of the minimum of the bond energy, k_θ is the angle force constant, θ is the angle, θ₀ is the location of the minimum of the angle energy, k_φ is the dihedral angle force constant, n is the multiplicity of the angle, φ is the dihedral angle, δ is the location of the desired dihedral angle, k_ω is the improper dihedral angle force constant, ω is the improper dihedral angle, and ω₀ is the desired improper dihedral angle. A 1-3 exclusion principle was used for nonbonded interactions and the 1-4 Coulombic interactions were scaled by a factor of 0.4 to be consistent with the CHARMm force field.

For simulations in implicit solvent, a distance-dependent dielectric (52) was used. The functional form used is given by ε(r) = αr, (with α = 1) consistent with previous simulations of β-peptides (2). As discussed in the Introduction, this method can exacerbate the attraction between oppositely charged atoms. To overcome this deficiency, it has been suggested that proteins be simulated in their neutral state. (49) Lennard-Jones interactions are cut and shifted at 40 Å to minimize the effect of truncating the potential. A force-shifted potential for the Coulombic interaction was used with a cutoff at the same length as that for the Lennard-Jones interactions.

For simulations in explicit solvent, the GROMACS 3.0 (53–55) simulation package was used. The TIP3P model (46) of water was selected for explicit solvent simulations because it is compatible with the CHARMm force field. Lennard-Jones interactions were truncated with a twin-range scheme at 10 and 15 Å. The electrostatic interactions were calculated using a particle-mesh Ewald technique (56) with a short-range cutoff of 10 Å, a maximum relative error of 10⁻⁵, and a fourth-order spline. In solution, these peptides are expected to have protonated β³-homolysine residues and N-termini, with each peptide having a +4 charge. To counter the positive charge of each peptide, four chloride ions were included in the simulation cell. It should be noted that simulations (23) of charged β-peptides with and without counterions suggest that counterions stabilize the helix (vis-à-vis simulations without counterions). We used 1849 water molecules and a cubic box with a length in the vicinity of 38 Å. Molecular dynamics simulations were performed at constant pressure (1 bar) and temperature (300 K) using the Berendsen method (57). The thermostat had a coupling of 0.2 ps and the barostat had a coupling of 0.1 ps and a compressibility of 0.45 × 10⁻⁴ bar. The simulations were run with a time step of 0.0005 ps over a period of 2 ns, and the properties were averaged over the last 1.5 ns.

Throughout the simulations the helicity, number of hydrogen bonds, and energies were calculated. The helicity of the peptide was calculated from the dihedral angles φ (C(=O)-N-C_β-C_α) and ψ (C_β-C_α-C(=O)-N) using the expression

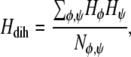(2)

where N_φ,ψ is the number of φ- or ψ-angles. The quantity H_φ is defined as

(3)

and a similar definition exists for H_ψ. The parameters a, b, φ_o, and ψ_o depend on the type of helix. For the 14-helix a = 20°, b = 39°, φ_o = −135°, and ψ_o = −140°, while for the 12-helix a = 20°, b = 39°, φ_o = 95°, and ψ_o = 103°. We also determined the overall potential energy and its various contributions, including Lennard-Jones and electrostatic energies.

Potential of mean force

The free energy associated with the forced unfolding of the molecules can be quantified through a potential of mean force (or PMF). That PMF can be determined as a function of peptide end-to-end distance, and represents the reversible work required to compress or extend the peptide from its equilibrium end-to-end distance. Several different methods exist to calculate the potential of mean force. In this work we use two of these methods: the expanded-ensemble density of states (EXEDOS) and a constraint-force (CF) approach. EXEDOS (58) calculations are based on a stochastic algorithm that ensures uniform sampling along a reaction coordinate. That uniformity is achieved by applying a set of weights along the reaction coordinate. Such weights are unknown a priori; they are estimated on-the-fly during the simulation. Upon convergence of a simulation, those weights correspond to the density of states along the specified reaction coordinate. From knowledge of the density of states, it is possible to calculate the PMF according to

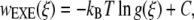(4)

where w is the potential of mean force, ξ is the reaction coordinate (the end-to-end distance of the molecule), k_B is Boltzmann's constant, T is the temperature of the simulation, and g(ξ) is the estimate of the density of states provided by the simulation. Parameter C is an arbitrary constant chosen in such a way that the minimum in w is zero. Some of the benefits of the EXEDOS method include uniform sampling of the reaction coordinate, application of nonlocal moves that alter the peptide conformation, and periodic swapping of configurations between boxes that reduce the risks of getting trapped in local energy minima. We use our own code to perform EXEDOS calculations in implicit solvent. We use translation of atoms, pivot moves, and hybrid-MD moves to sample the conformational space of the protein. Consistent with our previous simulations of β-peptides, each stage progresses with a modification of the convergence factor according to ln 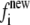= 0.5 ln 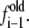The simulations are stopped once the convergence factor f reaches 10⁻⁵. Throughout the simulation, the average force in each bin is determined along the reaction coordinate. The force is then used to determine a separate estimate of the PMF. This provides a way to verify the internal consistency of our calculations.

While EXEDOS simulations are highly effective in implicit solvent models, they can be highly computationally demanding for explicit solvent simulations. For calculations of the PMF in explicit water we therefore resort to a CF approach and molecular dynamics simulations. A recent summary and comparison of methods to determine the PMF using molecular dynamics indicates that calculations based on the constraint force provide optimal results (59). As its name implies, the potential of mean force is related to the forces experienced along the reaction coordinate. One can obtain the PMF by integrating over the force according to

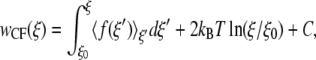(5)

where w is again the potential of mean force, ξ is the reaction coordinate, and 〈f(ξ′)〉_ξ′ is the mean force at a particular value of ξ′. In our calculations, the simulations are run by constraining the reaction coordinate ξ to a specific value and monitoring the force required to constrain the simulation at that value. We perform the simulation at several values of the reaction coordinate and integrate using Eq. 5. The simulations were prepared by first running 200-ps NPT simulations without bias, then pulling to the value ξ_i by temporarily adding a harmonic potential over 100 ps. After applying the constraints, we performed simulations with an equilibration period of 2.5 ns, followed by a production simulation of 1.5 ns. Over the equilibration period, the peptides lost some of their helical character and underwent partial conformational changes.

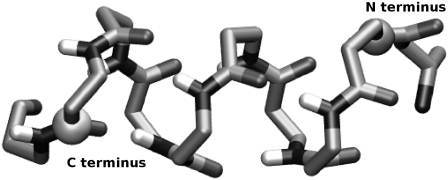
Our reaction coordinate, ξ, is defined as the distance from the nitrogen of the N-terminal residue to the carbonyl carbon of the C-terminal residue. To avoid the fluctuations inherent to the first and last residues, the second and penultimate residues are selected. The chosen sites are illustrated in Fig. 4.

FIGURE 4.

The reaction coordinate used in this article. The backbone is shown as sticks and the spheres represent the atoms used to define the reaction coordinates. The end-to-end distance, ξ, is defined as the separation between the nitrogen on the N-terminus and the carbonyl carbon of the C-terminus. Side chains and hydrogens (except for backbone N-H hydrogens) have been removed for clarity. This figure was created using VMD (77).

RESULTS

Potential of mean force and structure

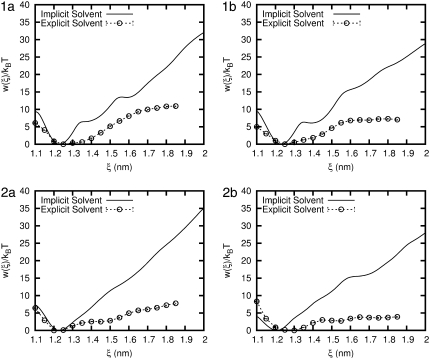
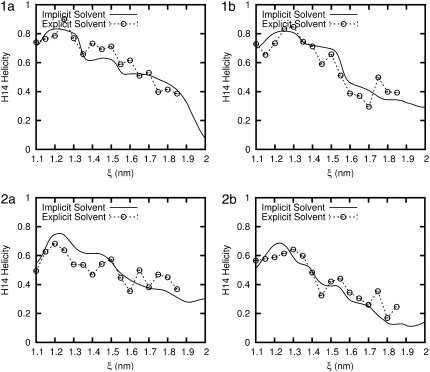
To directly compare the various solvent models, the PMF from the two solvent models considered in this work are plotted for each peptide in Fig. 5. The corresponding helicity (for the 14-helix) is given in Fig. 6. The first salient feature of our results is that, for all the β-peptides considered here, the implicit solvent model overestimates their mechanical stability considerably (vis-à-vis that predicted in the more realistic explicit water model). For peptides 1a, 1b, and 2a, the equilibrium end-to-end distance (the minimum in the PMF) is ∼ξ_eq = 12.2 Å for the implicit solvent and 12.5 Å in explicit water. This result is consistent with our expectations, given the expected length of 1.56 Å per residue (1) for an ideal 14-helix, and the fact that eight residues separate the atoms that define the reaction coordinate. For peptide 2b the equilibrium end-to-end distance is ξ_eq = 12.1 Å, and in explicit water it is close to 13 Å. In other words, the explicit solvent favors a configuration that is almost 10% longer. For all four peptides, the minimum in the PMF is associated with a maximum in the helicity (see Fig. 6). The helicity is comparable in the two solvent models, indicating that the equilibrium folded structure of the peptides is a relatively robust property.

FIGURE 5.

Comparison of the potential of mean force (PMF) for each β-peptide in implicit and explicit water. Error bars are shown for the explicit water result and are the size of the symbols.

FIGURE 6.

Comparison of the average H14 helicity (using Eq. 3) for each β-peptide in implicit and explicit water. Error bars are shown for the explicit water result and are the size of the symbols.

Potential energy contributions

Throughout the simulation, the potential energy is recorded as a function of reaction coordinate, and the resulting change in energy (denoted by ΔU) from that corresponding to the minimum of the PMF is plotted in Fig. 7. The peptides in implicit solvent exhibit an increase of 30–50 k_BT as ξ is increased from its equilibrium value to 20 Å. For the β-peptides in TIP3P water, the potential energy does not exhibit any clear trend. Depending on the specific value of ξ, one can detect local oscillations of ΔU, but these are at most ∼10 k_BT. Even at the longest extensions considered in our simulations (∼20 Å), the potential energy continues to be within a few k_BT of that corresponding to equilibrium.

FIGURE 7.

Comparison of the total potential energy for each β-peptide in implicit and explicit water. Error bars are shown for the explicit water result and are the size of the symbols.

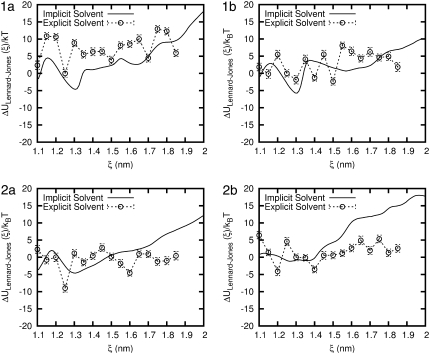
The Lennard-Jones contribution to the potential energy is also calculated for the two solvent models and is shown in Fig. 8. The implicit solvent model shows an increase of between 10 and 20 k_BT at 20 Å. For all four peptides, the Lennard-Jones energy in implicit solvent exhibits a minimum at ∼ξ = 13.1 Å. This minimum arises at a value of the end-to-end distance that is slightly larger than that corresponding to equilibrium (ξ_eq). In contrast, in our explicit water simulations the potential energy does not change significantly, and it does exhibit a local minimum at a value that coincides with ξ_eq.

FIGURE 8.

Comparison of the Lennard-Jones energy for each β-peptide in implicit and explicit water. Error bars are shown for the explicit water result.

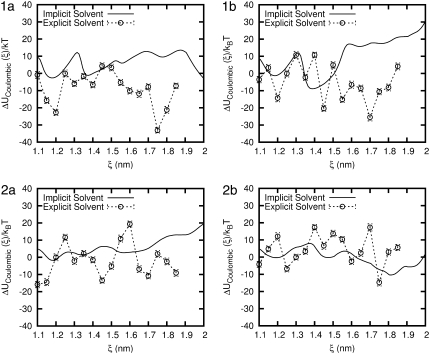
Fig. 9 shows the electrostatic or Coulombic contribution to the potential of mean force, denoted by ΔU_Coulombic. For the peptides in implicit solvent, ΔU_Coulombic exhibits several, well-defined local minima with increasing ξ. The depth of these minima can be relatively large, reaching ∼30 k_BT in some cases. For all four peptides, the first local minimum occurs at a value of ξ that is smaller than ξ_eq. It is the balance between a Coulombic minimum at ξ < ξ_eq and a Lennard-Jones minimum at ξ > ξ_eq that gives rise to the observed minimum in the PMF. The behavior in explicit water is considerably different. Peptides 1a, 1b, and 2b exhibit a minimum is ΔU_Coulombic that coincides with ξ_eq or is only slightly below ξ_eq. In contrast, for molecule 2b, the minimum in ΔU_Coulombic occurs at relatively small ξ, on the order of 11 Å. For all four peptides, we find that the local minimum in ΔU_Coulombic that corresponds to ξ_eq is not the absolute minimum for the range of ξ considered in this work; in general, the Coulombic interactions favor less compact helices and values of the end-to-end distance that are much longer than ξ_eq.

FIGURE 9.

Comparison of the Coulombic energy for each β-peptide in implicit and explicit water. Error bars are shown for the explicit water result.

Entropic contribution

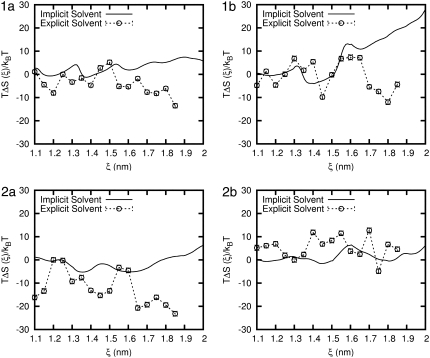
The entropic contribution to the free energy is calculated using the relationship TΔS = ΔU – w. Fig. 10 provides TΔS for all four peptides in the implicit and explicit solvent models. In the implicit solvent, for all peptides TΔS exhibits multiple minima. For all four peptides, the first local minimum occurs in the vicinity of 12 Å, which is slightly below ξ_eq. A second, relatively pronounced minimum appears for peptides 1a, 1b, and 2a at approximately ξ ∼ 13.7 Å. That second minimum also appears to arise for peptide 2b, but it is barely noticeable. For peptides 1a, 1b, and 2a a third minimum arises at ξ ∼ 16 Å (or slightly above that value). For peptide 2b the third minimum occurs at ξ ∼ 14.5 Å, and a fourth minimum is found at ξ ∼ 18.2 Å. Note that a weak shoulder can also be detected in TΔS for the other peptides in the vicinity of ξ = 18 Å. For peptides 1a, 1b, and 2b, beyond a distance of ∼16.5 Å, the entropic term increases monotonically with ξ. For peptide 2a, the entropic term remains approximately constant, even beyond end-to-end distances of 16.5 Å.

FIGURE 10.

Comparison of the entropic contribution to the PMF for each β-peptide in implicit and explicit water. Error bars are shown for the explicit water result and are the size of the symbols.

For peptide 1a, the results for TΔS in explicit water exhibit a number of similarities with those obtained in the implicit solvent. For peptide 1a we observe three local minima at approximately the same values of ξ than in the implicit solvent case. For peptide 1b the first and second minima also appear at values of ξ that are similar to those for the implicit solvent. In contrast, for peptides 2a and 2b TΔS in explicit water has little resemblance to that obtained with an implicit solvent. The positions of the minima are different and, in the particular case of peptide 2a, the magnitude of the entropic term is much larger in explicit water.

The differences in the PMF obtained with the two solvent models are particularly pronounced at extensions beyond 15 Å, where we observe an increase in entropy with the implicit solvent model and a decrease in entropy with the explicit solvent model. In the implicit solvent model, one neglects the solvent entropy and measures only the peptide entropy. At larger end-to-end distances the peptide can adopt more configurations. However, in the explicit solvent, the system entropy includes an explicit contribution from the solvent. If one assumes that the peptide entropy is comparable in both solvent models, then the decrease in entropy of the system at large end-to-end distances stems from a decrease in the entropy of the water itself. The water becomes more ordered at large end-to-end distances. By neglecting the entropic contributions of the water, the implicit solvent model overestimates the peptide's stability. We also note that, because the ΔU term can be fairly constant for some peptides, it is possible to have a PMF that is dominated by the entropic term.

Role of water

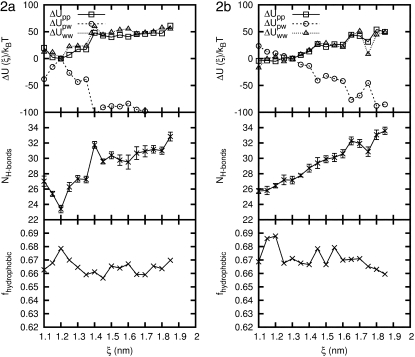
To quantify the effects of solvent more clearly, we now examine the properties of the peptide and explicit water system as a function of ξ. Figs. 11 and 12 show the potential energy of interaction of the peptide with itself (only the nonbonded and torsional contributions to the energy are included in ΔU_pp), the peptide with water (ΔU_pw), and the water with itself (ΔU_ww only includes nonbonded interactions). For each peptide, the intramolecular energy increases by ∼50 k_BT as the molecules are stretched from their equilibrium value to end-to-end distances in the range of 18.5 Å. For the four peptides considered here, ΔU_pp exhibits a slight local minimum at ξ ≈ 12 Å, which is slightly below ξ_eq. From a strictly intramolecular point of view, the unfolding of the helical structure is clearly unfavorable.

FIGURE 11.

Properties of β-peptide 1a and 1b in explicit water simulations at T = 300 K as a function of end-to-end distance. (Top) Contributions to the potential energy: peptide-peptide, peptide-solvent, and solvent-solvent interactions. (Middle) Number of hydrogen bonds between the peptide and water. (Bottom) Fraction of hydrophobic solvent-accessible surface area of the peptide. Error bars are shown for the hydrogen bonds; otherwise, error bars are the size of the symbols.

FIGURE 12.

Properties of β-peptide 2a and 2b in explicit water simulations at T = 300 K as a function of end-to-end distance. (Top) Contributions to the potential energy: peptide-peptide, peptide-solvent, and solvent-solvent interactions. (Middle) Number of hydrogen bonds between the peptide and water. (Bottom) Fraction of hydrophobic solvent-accessible surface area of the peptide. Error bars are shown for the hydrogen bonds; otherwise, error bars are the size of the symbols.

Interestingly, the contributions to the energy from water-water interactions (ΔU_ww) follow a trend that is similar in shape and magnitude to that of peptide-peptide interactions. In contrast, the increase in ΔU_pp and ΔU_ww is compensated by a pronounced decrease of the energy of interaction between the peptide and the solvent (ΔU_pw) which, for the longest extensions considered in this work, can be as large as −100 k_BT. For all peptides, the shape of ΔU_pw is almost a mirror image of that of ΔU_pp. Increases of ΔU_ww and ΔU_pp are counteracted by decreases in ΔU_pw, in such a way as to provide a total energy that is somewhat insensitive to ξ, as already shown in Fig. 7. The nature of the drop in ΔU_pw varies from peptide to peptide. For molecules 1a and 2b, the decrease is relatively steady. For molecule 1b, ΔU_pw is much more jagged and it exhibits sharp changes of up to ∼50 k_BT. Molecule 2a is somewhat different in that, at ξ = 14 Å, ΔU_pw drops abruptly and remains relatively low and uniform for ξ-values longer than that.

The changes in energy shown in Figs. 11 and 12 can be partly explained by analyzing the number of hydrogen bonds between the peptides and water as a function of ξ. That number was determined using the GROMACS utility g_hbond (53). Figs. 11 and 12 show the results. For concreteness, we focus on peptide 2a, which exhibits an abrupt drop in ΔU_pw at a value of ξ = 14 Å (see Figs. 11 and 12). That drop can be interpreted in terms of the structure of the peptide. At small values of ξ the molecule adopts a helical configuration, and is able to form multiple hydrogen bonds with itself. At ξ = 14 Å many of those internal hydrogen bonds are broken and, as shown in Fig. 12, they are replaced by the formation of approximately eight new hydrogen bonds between the peptide and water. If the formation of a peptide-solvent hydrogen bond is ∼10 k_BT (60), then a 100 k_BT drop in peptide-solvent energy could be explained all or in part by the formation of hydrogen bonds. Similar observations can be made about the other three peptides, although in that case the increase in hydrogen bonds between peptide and water with stretching is much more gradual.

As the peptide end-to-end distance grows, more peptide atoms are exposed to water, resulting in a decrease in ΔU_pw. What was unknown a priori was that the solvent-solvent energy for each peptide increases almost as much as the peptide-peptide energy. A sum of all these energies leads to the relatively uniform net potential energy profiles shown in Fig. 7. The favorable peptide-solvent interactions are canceled out by the peptide-peptide and solvent-solvent interaction energy. The observation that, as the molecule is stretched, water-water hydrogen bonds are replaced by peptide-water hydrogen bonds to give a uniform potential energy profile, suggests that entropic effects can therefore play a determining role in the stability of β-peptides.

The interaction of solvent with peptide can also be quantified by calculating the solvent-accessible surface area (SASA) of the peptide. We determined the total SASA of the peptide as well as the hydrophobic and hydrophilic SASA using the GROMACS utility g_sas (53,61). The fraction of hydrophobic surface area was between 0.6 and 0.7, which makes sense with 6:10 hydrophobic residues for these peptides. Each measure of the SASA increases with ξ, but at a different rate. This leads to a small decrease in the fraction of hydrophobic SASA (Figs. 11 and 12), which makes the peptide-water interaction more favorable at larger ξ.

Temperature effects on potential of mean force

An examination of the enthalpic and entropic contributions to the PMF provides the basis for intriguing predictions regarding the stability of peptides as a function of temperature. By examining the relative sign and magnitude of ΔU (Fig. 7) and TΔS (Fig. 10), we can predict how the pulling of peptides might respond to changes in temperature.

As shown in Figs. 7 and 10, peptides 1a and 1b both exhibit mostly positive values of ΔU and small negative values of TΔS along the reaction coordinate; they are stabilized by enthalpic interactions. For these peptides, increasing T would destabilize the peptide. Peptide 2a exhibits a negative ΔU and negative TΔS; it is stabilized by entropic interactions. A decrease in temperature would therefore lower the relative importance of the entropic term and decrease the PMF. In contrast to its isomer, the enthalpic and entropic terms of peptide 2b exhibit relatively little change upon pulling; it should be insensitive to small changes in temperature.

We also used the weighted histogram analysis method (62) to determine how each peptide might respond to changes in temperature. The probability distribution can be reweighted from the simulation temperature to another temperature using the potential energy of the simulations according to the equation

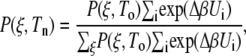(6)

where T_n and T_o are the reweighted and simulation temperatures, Δβ = (1/k_BT_n) – (1/k_BT_o), and U_i values are the potential energies from the simulation at T_o. The probability distribution is obtained from the PMF using P(ξ) = −k_BT ln w(ξ) at 300 K. Our weighted histogram analysis method results are in agreement with the examination of ΔU and TΔS presented above.

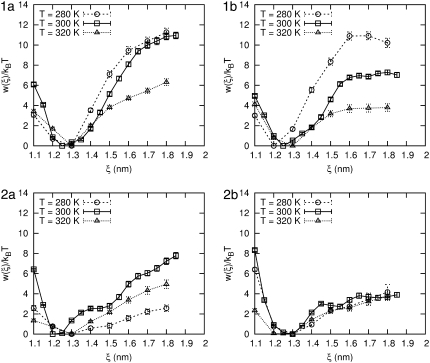
Because of these intriguing predictions, we performed CF molecular dynamics simulations at low (280 K) and high (320 K) temperature to obtain the PMF. The results are shown in Fig. 13 and are in agreement with the analysis of the enthalpic and entropic terms to the PMF at 300 K. Peptides 1a and 1b are destabilized upon heating. In analogy to force spectroscopy experiments, pulling these two peptides should be easier at higher temperatures than at lower temperatures. For peptide 1b it is interesting to note that the plateau for ξ > 16 Å exists at each temperature. The PMF of peptide 2b exhibits little change with temperature. Perhaps more interestingly, peptide 2a exhibits a destabilization at lower temperatures that is shown in a shift of ξ_eq from 12 Å to 13 Å, and a significant decrease in the PMF at 18 Å from 7 k_BT (at 300 K) to 2 k_BT (at 280 K).

FIGURE 13.

The PMF at 280, 300, and 320 K for each β-peptide in explicit water. Error bars are shown for each condition.

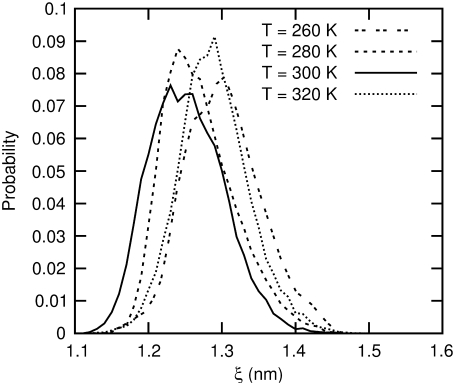
We further characterized this temperature behavior by running NPT molecular dynamics simulation of all four peptides at 260, 280, 300, and 320 K for 10 ns without constraints or biases. The results for peptide 2a are shown in Fig. 14. At 280 and 320 K, we see a shift of ξ_eq from 12 to 13 Å. The result at 260 K indicates a further shift of ξ_eq to higher values and a broadening of the probability distribution.

FIGURE 14.

The probability distribution of end-to-end distance for β-peptide 2a in explicit water at various temperatures.

It is widely known that proteins are generally denatured or unfolded by high temperature. A smaller class of proteins, however, are destabilized by low temperatures (63); cold-denaturing proteins include myoglobin (64), staphylococcal nuclease (65), and barstar (66). To our knowledge, peptide 2a represents the first example of a synthetic peptide that undergoes cold-induced destabilization. Similar to 2a, the melting transition of cold-denaturing proteins exhibits large negative values of ΔU and TΔS, as recently determined for the yeast protein frataxin (67) and exhibited in myoglobin (64). Gademann et al. (68) examined the effects of temperature on β-peptides in methanol using nuclear magnetic resonance and circular dichroism spectroscopy, but only between 298 and 393 K and so could not observe evidence of cold-induced denaturing.

DISCUSSION

Overall, the picture that emerges from our simulations is that the helical, folded structure of the four peptides considered in this work is a result of a delicate balance between intramolecular interactions and hydrophobic, water-mediated interactions. Contrary to previous beliefs, our results indicate that intramolecular interactions are only partly responsible for the helical conformation of the β-peptides.

In the case of peptides 1a and 1b, it is observed that the presence of two ACHC groups per turn does confer higher mechanical stability to the molecules than the presence of one ACHC and one β³-homophenylalanine per turn (molecules 2a and 2b). It is also found that, for peptides 1a and 1b, the particular sequence of the residues (i.e., whether they are ordered or scrambled) does not affect mechanical stability in a major way. What does depend on sequence, however, is the role of enthalpy and entropy on folded and unfolded conformations. The end-to-end distance of the ordered peptide (molecule 1a) can fluctuate more easily in the range 12 < ξ < 13.5 Å than that of the scrambled peptide (molecule 1b) with the same chemistry.

These results also have important implications for the use of implicit solvent models. One common treatment of water in protein simulations is the generalized Born (GB) model (69–71). Several groups have reported comparisons of some of these models with explicit water simulations (72–76). Using α-peptides, these works have shown that the GB models can overstabilize helices compared to explicit water. Specifically, Zhou (74,76) has found an increase in helical content when using the GB model compared to explicit water simulations. In agreement with previous simulations, our results for β-peptides indicate that, while a simple implicit solvent model (in which only intramolecular interactions are included) is able to describe the folded structure of the peptides, that model is unable to describe the true origins of that folded structure, the response of the molecule to changes in temperature, or the ability of the molecules to withstand tensile forces. In contrast to previous work, we do not observe a difference in helical content between the explicit and implicit solvent models for the β-peptides considered in this work. While implicit solvent models are helpful because they facilitate sampling of protein conformational space, this comes at the expense of the solvent details, which in our case play a central role in the enthalpic and entropic balance that controls the folded structure of our molecules.

CONCLUSION

We have studied the potential of mean force associated with the extension of four helical β-peptides using implicit and explicit solvent models, and find that the peptides in explicit solvent are quantitatively less stable than in the implicit solvent. The folded structures of the peptides are qualitatively similar, as evidenced by the agreement of peptide helicity as a function of end-to-end distance. The origin of the decreased stability in TIP3P water can be traced to the solvent entropy and solvent enthalpy, which change appreciably as the end-to-end distance of the peptide changes. In general, the potential energy of the implicit solvent systems increases and the explicit solvent systems remain more constant with end-to-end distance. This leads to an increase in entropy in implicit solvent and a decrease in entropy in explicit solvent as the peptide is stretched. In the explicit solvent, favorable peptide-solvent interactions counterbalance the unfavorable peptide-peptide and solvent-solvent interactions. We also see an increase in the number of peptide-water hydrogen bonds as the peptides are extended and a decrease in the fraction of hydrophobic surface area, both of which affect the solvent entropy and enthalpy. Analysis of the enthalpic and entropic terms lead to the prediction of a synthetic peptide that destabilizes upon pulling at lower temperatures, reminiscent of naturally occurring cold-denaturing proteins. While the experimental literature of temperature effects on the stability of β-peptides is limited, we hope that the predictions outlined in this article will motivate more characterization work aimed at assessing the relative importance of entropic and enthalpic forces in this intriguing class of molecules.

While the use of implicit solvent models has important computational advantages, the simplifications involved can lead to discrepancies in the free energy of particular peptide conformations. An important finding of this work has been to show that both implicit and explicit solvent models lead to similar equilibrium folded structures. Upon small deviations from equilibrium, such as those encountered upon pulling a β-peptide, we find that the behaviors predicted by explicit and implicit solvents are qualitatively different. For some β-peptides, we find that the entropy of the solvent plays a significant role in the folding of the molecule. The observation of a cold-destabilizing peptide could not be observed using the implicit solvent model. These observations have significant consequences for studies of the aggregation or self-assembly of β-peptides in solution, and suggest that a fully atomistic approach that includes explicit water will be necessary to describe such phenomena.