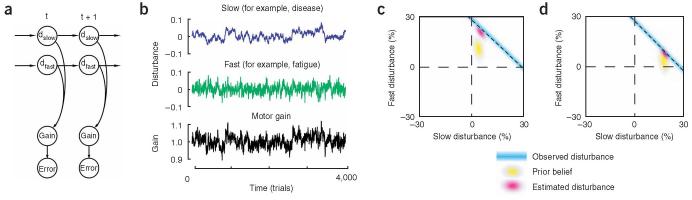
Figure 1.

A generative model for changes in the motor plant and the corresponding response of a Bayesian learner to performance errors. For illustrative purposes, here we show the results of a simulation with just two timescales. a) Various disturbances d evolve over time as independent random walks that linearly combine to change the motor gain. The observed error is a noisy version of the gain disturbance. b) Sample disturbances and the resulting motor gain. c) The Bayesian learner’s belief during an experiment where a disturbance suddenly increases the gain of the motor plant. Before the learner observes the gain, it has a prior belief. The learner’s belief can be represented by its current estimate of the fast and slow disturbances and its uncertainty about this estimate. This is termed a prior and is shown in yellow. In this case, the prior has a larger uncertainty along the fast state. In each trial, the learner observes the disturbance to the motor gain (in this case a 30% increase). This observation is represented by the blue line. The observation is a line and not a point because the disturbance could be due to a fast timescale with magnitude of 30%, a slow timescale with magnitude of 30%, or any other point along this line. Because the learner has sensory noise, there is a probability distribution associated with its observation, and therefore the blue line is hazy. To solve the credit assignment problem, the learner integrates its observation (blue line) with the prior belief (yellow cloud) to generate a posterior estimate (red cloud). In this case, because uncertainty was greater for the faster timescales, the observation was mostly assigned to a fast timescale perturbation. d) The perturbation is sustained for 30 trials. Now the learner associates the perturbation with a slow timescale.