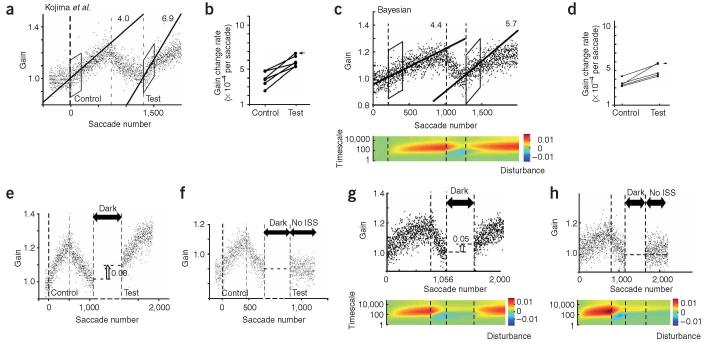
Figure 3.

The double reversal paradigm. a) The gain is first adapted up until it reaches about 1.2 with a target jump of +35%. Then it is adapted down with a target jump of -35%. Once the gain reaches unity it is again adapted up with a positive target jump. Data from Kojima et al¹³. The box indicates the trials where the line was fitted. The number on the line indicates its slope. b) The speed of adaptation (slope of the lines in part a) is compared between the first gain-up and the second gain-up trials in different sessions of training. The monkey exhibits savings in that it re-learns faster despite the apparent washout. c) The performance of the Bayesian learner is shown along with a colorplot showing the estimate of the learner of the disturbance at each timescale. d) The rate of adaptation for the Bayesian learner. e) In this experiment, the reversal training is followed by a period of darkness, and then gain-up adaptation¹³. Saccade gain shows spontaneous recovery. f) The same plot for the Bayesian learner along with a colorplot showing the estimate of the disturbance at each timescale. g) In this experiment, the period of darkness is followed by a condition where the target does not change position during the saccade period (i.e., no intra-saccadic step, ISS)¹³. The animal does not show spontaneous recovery. h) The same plot for the Bayesian learner along with a colorplot showing the estimate of the disturbance at each timescale..