Altruism Among Relatives And Non-Relatives

Abstract

Hamilton’s (1964) kin-selection theory predicts that altruism will be greater with greater genetic overlap (degree of kinship) between giver and receiver. Kin may be identified in terms of social distance – the closer you feel to someone else, a) the greater your genetic overlap with them should be, and b) the more altruistic you should be toward them. The present experiment determined the amount of their own (hypothetical) monetary reward undergraduates were willing to forgo in order to give $75 to other people at various social distances. We found that a) genetic relationship and b) altruism varied inversely with social distance; the closer you feel toward someone else, the closer their relation to you is likely to be, and the more altruistic you are likely to be toward them. However, even at the same social distance, participants were willing to forgo significantly more money for the benefit of relatives than for the benefit of non-relatives. These results are consistent with kin-selection theory and imply that altruism is determined by factors in addition to social distance.

Introduction

Altruism has been defined in economic terms as “costly acts that confer economic benefits on other individuals” (Fehr & Fischbacher, 2003, p. 785) where the costs and benefits are unspecified. A biological definition of altruism: “acting to increase another individual’s lifetime number of offspring at a cost to one’s own survival and reproduction” (Krebs & Davies, 1993, p. 265) is consistent with the economic definition but specifies both costs (“one’s own survival and reproduction”) and benefits (“increase [in] another individual’s lifetime number of offspring”).

On the surface, biological altruism seems inconsistent with natural selection. Why sacrifice one’s own survival and reproduction for the benefit of another organism? However, according to Hamilton’s (1964) kin-selection theory, although individuals may act altruistically, natural selection acts fundamentally on genes and genes are never altruistic. Altruistic behavior would then depend on the coefficient of relatedness, r (the probability that a gene in the giver is an identical copy, by descent, of a gene in the receiver). With a given cost to the giver and benefit to the receiver, the greater is r, the higher is the probability that biologically altruistic behavior will be observed. But how are relatives recognized? According to Krebs and Davies (1993, p. 275), “individuals may use a simple rule, for example ‘treat anyone in my home as kin.’” Although such a simple rule may suffice for some non-human species, in human societies, relative-recognition rules would be expected to be more complex.² Moreover, often in human society (and occasionally in non-human society), altruistic behavior is observed among non-relatives. Such acts may occur, consistently with kin-selection theory, because the originally tight connection of kinship with social propinquity has become weaker as human society has become more complex. Altruism in humans may depend directly on perceived social distance (as determined by overlapping spheres of activity at home, in the neighborhood, at work, and at recreation) and only indirectly on genetic relationship. Genetic overlap is not detectible in itself. Relatedness cannot act except through other factors such as physical resemblance, common interest, a history of reciprocation, or physical closeness. Among the Hiwi foragers in Venezuela, for example, it is common for families to share food with each other. Degree of relatedness is a very strong determinant of whether one family shares food with another. But relatedness acted almost wholly through residential closeness and reciprocation. Independent of these factors, relatedness itself had almost no influence in food sharing between families. (Kaplan & Gurven, 2005).

It is possible that, whereas we may be more likely to perceive relatives than non-relatives as socially close, once social closeness is established, we will be no more altruistic toward a relative than toward a non-relative at the same perceived social distance.³ The purpose of the present study was to test this possibility.

Prior experiments in our laboratory (Jones & Rachlin, 2006; Rachlin & Jones, 2008) determined the maximum amount of money participants were willing to forgo (the “cost”) in order to give $75 (“the economic benefit”) to other people at various social distances from them. Social distance was varied by asking participants to imagine that they had made a list of the 100 people closest to them with 1 being the closest, 2 being the second closest, and so forth (but not to actually make the list). Social distance (N) was defined as rank order on the list. Then, at each of a series of social distances, participants chose (hypothetically) between a fixed amount of money (usually $75) for the person at that social distance and a series of increasing or decreasing amounts of money for themselves. The amount of money for the giver equal in value to $75 for the receiver (the “crossover point”) was taken as a measure of altruistic tendency. Maximum amount forgone is taken here as a measure of altruism. Suppose John prefers $75 for Person #10 on his list to $25 (but no more than that) for himself; that is, John is willing to forgo up to $25 for #10’s benefit. Mary, on the other hand, prefers $75 for Person #10 on her list to $50 (but no more than that) for herself; that is, Mary is willing to forgo up to $50 for #10’s benefit. Because Mary is willing to forgo more money for the benefit of an equivalent person on her list, to that extent, she is more altruistic than John.⁴

The greater N was, in these prior studies, the less money participants were generally willing to forgo at the crossover point. Equation 1, a hyperbolic discount function of the same form as delay and probability discount functions (Green & Myerson, 2004; Jones & Rachlin, 2006; Rachlin & Jones, 2008) described the results:

$$v=\frac{V}{1+k_{\mathit{social}}N}$$ (1)

where V = the undiscounted reward value; v = the crossover point; k_social = a constant that varied across individuals. The greater was a person’s k_social, the steeper the discount function, the lower the crossover points across the range of N’s, the less altruistic that person was. The present study repeated the above procedure but participants also identified their relationship to the person at each N-value tested.

Materials and Methods

The above procedure was repeated with 206 Stony Brook undergraduates except, after each crossover point was obtained, participants indicated person-N’s relationship to them.

Participants first received these instructions:

• The following experiment asks you to imagine that you have made a list of the 100 people closest to you in the world ranging from your dearest friend or relative at position #1 to a mere acquaintance at #100. The person at number one would be someone you know well and is your closest friend or relative. The person at #100 might be someone you recognize and encounter but perhaps you may not even know their name.

• You do not have to physically create the list- just imagine that you have done so.

• Next you will be asked to answer a series of questions about a person at a given social distance. For each page, imagine the person who best fits the position (#1 to #100) and answer each question.

Crossover points were determined at 7 social distances. After each crossover point was determined, participants indicated their relationship to person-N (mother, father sister, brother, boyfriend, girlfriend, neighbor, roommate, etc.) by checking on a list.

Results

Crossover points for relatives (coefficient of relationship r ranging from .5 for parents and full siblings to .03125 for second cousins) were separated from crossover points for non-relatives – defined as those with r < .03125 (Wright, 1922). As expected, there were much higher percentages of relatives at near than at far social distances. The percent of relatives placed at N = 1, 2, 5, 10, 20, 50, and 100, was 72, 79, 50, 39, 28, 17, and 5 respectively.

Among relatives, participants tended to give more money to closer than to more distant ones. Figure 1 shows the fraction of $75 forgone by the giver to give $75 to a relative as a function of the coefficient of relatedness to the receiver – irrespective of social distance. Fitting a straight line to all (412) individual points, R² = .20. Thus, genetic overlap accounts for 20% of the variance of crossover points in this experiment.

1.

Median fraction of $75 participants were willing to forgo so as to give a relative $75 as a function of their coefficient of relatedness. The dashed line is the locus of equality. The error bars are standard errors of the mean.

The solid circles in Figure 2 are overall median crossover points at each social distance. The solid line shows Equation 1 fit to these points (R² = .983; k_social = .072). Because, as is typical in social discounting procedures, many participants preferred $75 for receivers at N = 1 or N = 2 to $75 for themselves, V was not fixed at $75 but was allowed to vary along with k_social. Obtained V = $87. Fitting Equation 1 to all (1027) individual crossover points, R² = .34. Thus, Equation 1 accounts for 34% of the variance of crossover points in this experiment.

2.

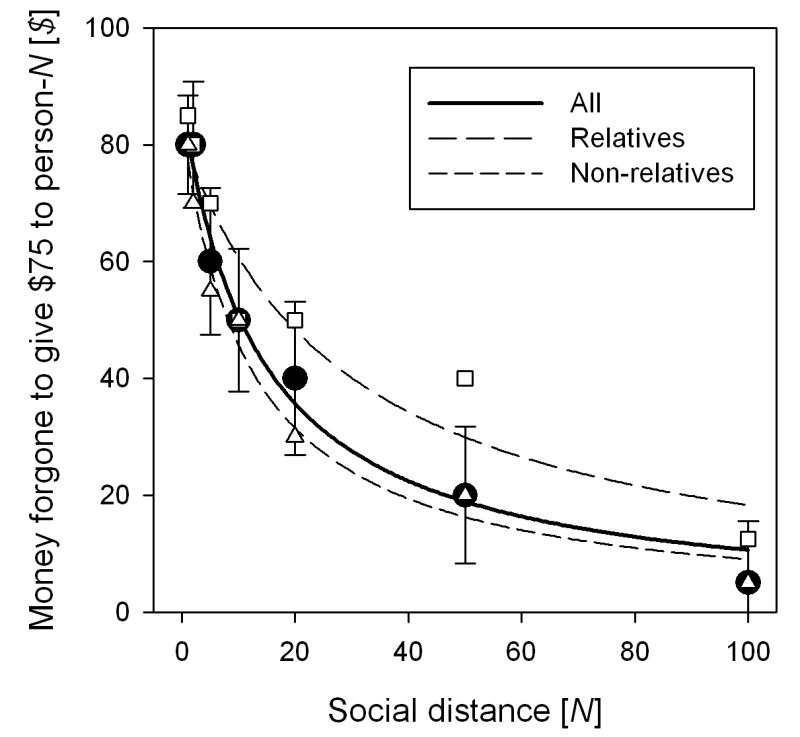
Social discount functions separated for relatives and non-relatives. The upper and lower dashed lines are Equation 1 fit to median crossover points for relatives (open squares) and non-relatives (open triangles). The solid line is Equation 1 fit to overall median crossover points (solid circles). The error bars are standard errors of the mean for the overall crossover points.

The open squares and triangles in Figure 2 are medians, at each tested social distance, of the crossover points for relatives and non-relatives separately. The upper dashed line is the fit of Equation 1 to the medians for relatives (R² = .925; k_social = .034; V = $82); the lower dashed line is the fit of Equation 1 to the medians for non-relatives (R² = .982; k_social = .083; V = $84). The crossover points for relatives are significantly higher than those for non-relatives [t(1004) = 14.319, p = .000].

From Figure 2 alone, it is not possible to say that any given participant was willing to give more money to relatives than to non-relatives. It is conceivable that participants who put more relatives on their lists were just more altruistic overall than those who put fewer relatives on their lists. To test whether higher generosity toward relatives than non-relatives holds within individuals, we determined, for each participant at each social distance, the deviation (+ or -) from the mean crossover point at that social distance. Then, for each participant, we averaged the deviations for relatives separately from the deviations for non-relatives. For example, if a participant placed relatives at social distances of 1, 2, 10, 20 and 50 and non-relatives at social distances of 5 and 100, the signed deviations for the 5 relatives were averaged separately from those for the 2 non-relatives (Across participants, the average deviation from the mean for relatives was +0.365 and for non-relatives was -0.144.) Then, again for each participant individually, we subtracted average deviation for non-relatives from that for relatives (The data of participants who cited only relatives or only non-relatives at all social distances were ignored.) Let us call this the “deviation difference.” A positive deviation difference for any individual indicates that that participant generally gave more money to relatives than non relatives independent of social distance. Across, participants the average deviation difference was +0.471, significantly above zero [t(191) = 3.249, p = .001] showing that individuals were more generous toward relatives than non-relatives.

Discussion

For these participants (mostly around 18 years old), altruism was strongly contingent on both closeness of genetic relationship and social distance. At almost every social distance, relatives were given more. These results imply that for humans at least there are factors other than those comprising our measure of social distance that determine altruistic behavior.

To speculate on what those factors may be we turn to the more general economic definition of altruism: “Costly acts that confer economic benefits on other individuals.” (Fehr & Fischbacher, 2003, p. 785). You might feel close to a friend because he or she is an entertaining person and fun to be with, but still not be willing to give him money. On the other side of the coin, you might feel indebted to a relative. Or, a relative, even one you might not like much, may be more likely to reciprocate your altruism than a friend would be, even at the same social distance. However, both the economic, and biological, definitions of altruism imply that, for behavior to be truly altruistic, costs be incurred by the giver and benefits go to the receiver. When “costly acts” are actually investments from which a return is expected, they may seem less costly than their nominal amounts and, to that degree, less altruistic.

In the light of such considerations, is it useful to refer to some acts as “altruistic” and others as “selfish?” Is there an altruism not in some way based on selfishness of the gene or due to delayed reinforcement (via reciprocation)? Rachlin (2002) has argued that some altruistic behavior (such as a woman running into a burning building to save someone else’s child or a soldier falling on a hand grenade to save the lives of other soldiers) cannot be explained in terms of genetic closeness or returns in social approval. Such acts, however, may be a part of long-term behavioral patterns that as patterns have high value for the individual – although the individual acts that comprise the patterns may have low value relative to their alternatives; the patterns are chosen as wholes because they are valuable only as wholes. Running into a burning building or falling on a hand grenade are of course not reinforced as individual acts and not valuable in themselves. But the patterns that such acts are part of – being a good person, living a moral life, obeying God – may be highly rewarding.

In this sense, altruism is like self-control. Smoking every individual cigarette, for instance, may be more valuable than its alternatives while smoking as a general pattern (a “habit”) is less valuable than not smoking. Choice of the more valuable larger pattern is nevertheless usefully considered self-controlled; similarly, choice of a more valuable social pattern may be considered altruistic. Just as delay discounting measures the tendency to prefer more valuable temporally extended rewards to immediate ones so social discounting measures the tendency to prefer more valuable socially extended rewards to selfish ones.