A collective mechanism for phase variation in biofilms

Abstract

Understanding how microbes gather into biofilm communities and maintain diversity remains one of the central questions of microbiology, requiring an understanding of microbes as communal rather then individual organisms. Phase variation plays an integral role in the formation of diverse phenotypes within biofilms. We propose a collective mechanism for phase variation based on gene transfer agents, and apply the theory to predict the population structure and growth dynamics of a biofilm. Our results describe quantitatively recent experiments, with the only adjustable parameter being the rate of intercellular horizontal gene transfer. Our approach derives from a more general picture for the emergence of cooperation between microbes.

From river rocks to tooth enamel, biofilms have insinuated themselves onto the world's surfaces (1, 2). Colonizing the surfaces of the world is no simple matter. It is widely held that a coordinated effort from many types of contributors that often involves sacrifices made by individual cells is required. Biofilms are a heterogeneous aggregation of microbial phenotypes (3, 4) that live together as a community, coordinating group activities, such as circulation, dispersion, and aggregate movement (5–9). The different types of cells rely on each other, so that their mutual interactions lead to the overall success of the group.

This coordinated group behavior within a microbial community is frequently referred to as “multicellular behavior” (10–13) to emphasize the importance of considering the structure of the community over the individual. Can local interactions between members of the community lead to global coordinated behavior of the biofilm? To address these issues in concrete terms, we show here that simple interactions between microbes mediated by mobile genetic elements (MGEs) (14–16) can explain quantitatively the important phenomena of phase variation (17, 18).

Phase variation is the phenomenon in which a single microbial biofilm changes its behavior and differentiates into several phenotypes. Given the central role different phenotypes play in the overall success of a community, phase variation is naturally central to the nature of biofilms. Phase variation has been found to occur via many different mechanisms (19–21), many of which are variations on a common theme of genetic rearrangements. Although most of the literature on phase variation focuses on internal rearrangements within a cell (19, 20), phase variation has also been documented to occur via interactions with genetic elements from outside of the cell (22). It has even been proposed that mobile genetic elements such as bacteriophage mu may have been the evolutionary precursors to phase variation by an internal genetic rearrangement (19).

The purpose of this article is to propose a minimal model by which MGEs acting between microbial genomes can bring about the phenomena of phase variation through a collective mechanism. Our model predicts that organisms within a biofilm have the inherent capacity to change their phenotypes, and that these phenotypes can stably coexist. We also examine the dynamics of phase variation and demonstrate that our model predicts features observed in experimental data on the formation of variants in biofilm cultures. For comparison with the available experimental data, the model solved here has been constructed with single organism biofilms in mind. However, in nature, biofilms often contain a plurality of species (12, 23). The theory presented here is not restricted to single organism biofilms but can be generalized to model multispecies biofilms.

The structure of this article is as follows: First, we review the phenomena of phase variation. We briefly mention various mechanisms for phase variation and focus on the examples that may best be explained by our model or that offer a precedent for our model. Next, we describe the statistical mechanics of horizontal gene transfer (HGT) and compute the steady states of our model, exhibiting in particular the coexistence of phenotypes. We use the model to simulate the population dynamics of biofilms and find that we are able to account for the key features of the available experimental data. We conclude by discussing our results and their broader implications for microbial ecosystems.

Evidence for the Participation of Mobile Genetic Elements

Microbes linked together into a biofilm often give rise to phenotypic diversity through the phenomena of phase variation. Phase variation has been defined as “oscillations in phenotype” or “on-off” switches in phenotype (24, 25). Both of these definitions capture the same element of sudden change in phenotypic characteristics, usually at a relatively high rate compared with other genetic mechanisms such as point mutations (20, 26). A review of how phase variation fits into the larger scheme of variation-producing mechanisms, especially with regards to frequency and time scales, is given in ref. 26.

The switching mechanism in phase variation often involves genetic rearrangements, such as inverted segments of DNA (19), mobile transposons (21), or expression of silent genetic material through homologous recombination (20). We now briefly highlight some examples of these phase variation mechanisms. Staphylococcus epidermidis is capable of forming variants that produce a polysaccharide intercellular adhesin (PIA) important in the formation of thick, multilayered biofilms. According to Zeibuhr et al. (21), the cause of 30% of the PIA-negative variants was found to be the insertion of insertion sequence element 256 (IS256) into and the subsequent inactivation of either the icaA or icaC genes. Furthermore, insertion of IS256 was found to be reversible and upon excision of IS256 the PIA phenotype was restored.

Koomey et al. (20) found that in Neissaria gonorrhoeae homologous recombination between a pilus gene in an actively expressed locus and several partial copies of pilus⁺ and pilus⁻ genes in silent storage loci drive the phase variation. Recombination with the different silent loci makes changes to the expressed pilus gene and thus changes the phenotype of the cell. In reverse, recombination events that return the gene to its previous form restore the former phenotype as well. Inactivation of recA leads to a 100- to 1,000-fold lower frequency of phase variation.

Although the particulars of these mechanisms may involve differing molecular reactions and pathways, they share two general features. First, they are reversible gene mutations for inducing a phenotypic change by genetically altering expression levels or the expressed products themselves. These mechanisms conserve the genetic material that causes the change. This conservation is an important factor in the heritability and stabilization of the phase variation behavior across generations. The stochastic nature of these genetic rearrangements, wherein each reaction possesses a forwards and a backwards rate and is in principle a chemical equilibrium, allows for the stable coexistence of phenotypes at consistent ratios—an important feature in natural biofilms and one that allows us to obtain reproducible experimental results that can be compared with theoretical predictions.

The second feature that these mechanisms share is that they involve solely internal genome rearrangements. However, it is known that microbes are not restricted to interacting with only their own genetic material. MGEs such as raw DNA, transposons, plasmids, and viruses, are capable of introducing external genetic material into a microbe (2, 14, 15, 16, 27). This external genetic material can then insert into or recombine with the cellular genome. MGEs can carry functional genes between organisms as in the case of HGT. MGEs can also integrate into a gene or its promoter region causing a disruption in that gene's expression. These mechanisms are similar to those of phase variation via internal genetic rearrangements (20, 21). The main difference is the communal nature of the rearrangements in the case of the MGEs. The MGEs allow for the exchange of genetic material between microbes whereas the internal genetic rearrangements do not.

Webb et al. (28) found that cells from a strain of Pseudomonas aeruginosa exposed to filamentous bacteriophage Pf4 underwent phase variation, switching to a small colony variant (SCV) phenotype. This bacteriophage is naturally associated with the strain of P. aeruginosa studied. The SCVs displayed the phenotypic traits of enhanced attachment. A common theme for biofilm development, enhanced attachment plays a crucial role in the dense packing, structure, and adherence of cells to the biofilm (3). Resch et al. (29) found spontaneous release of lysogenic phages in Staphylococcus aureus and postulated that phages are an important part of the biofilm state, playing a role in persistence and survival. Bacteriophages have been shown to regulate genes in Escherichia coli (30), leading to a change in host phenotype. While the precise nature of the interactions between viruses and biofilms is not clear, they appear to be an important part of the community dynamics.

Neissaria gonorrhoeae, as mentioned previously, has both an expression locus and silent storage loci that recombine, giving rise to phase variation (20). Transformation and recombination are known to play a large role in Neissaria. These pathogens are naturally competent, always ready to take up exogenous DNA from their environment. Furthermore, it was found that transformation, the act of taking up exogenous DNA from lysed cells, can increase the rate of phase variation. This rate increases most when the DNA that is taken up comes from a related but different strain of Neissaria (31). It is known that titration of the slip-strand repair proteins mutS and mutL play a role in increasing rate of phase variation by effectively increasing the rate of mutations. However, increasing the chemical concentrations of mutS and mutL only lessens the increase in the rate of phase variation, but does not eliminate it, raising the possibility of another mechanism acting in conjunction with the mismatch repair saturation (31, 32). Alexander et al. (31) wrote that “the other mechanism must also require DNA entry into the cell and a functional recA allele, because transformation and recombination deficient meningococci were not altered in their phase variation.” Additional recombination between the exogenous Neissaria DNA and the expression locus is one such possible mechanism for increasing the rate of phase variation (33).

Finally, conjugative DNA exchange and recombination has been observed in the genome of the hyperthermophile archaeon Sulfolobus acidocaldarius (34, 35). DNA exchange in S. acidocaldarius may not only serve as a mechanism for phase variation, but as a means for conjugative DNA repair (34).

Smith has shown that MGEs can serve to maintain certain types of cooperative behavior between microbes (36). When the benefits of virulence factors are shared by all members, and dependent on the total communal production of the virulence factor, MGEs horizontally transfer the virulence factor genes through members of the community. The communal nature of MGEs then drives the evolution of communal MGE-associated virulence factor genes, examples of “cosmopolitan genes” (37)—specialty genes whose presence is dictated by the environment, and are thus more characteristic of the environment than of a single organism.

In summary, even a biofilm grown from a single microbe is capable of producing a community consisting of several variant phenotypes, a phenomenon that is an important component for the survival and persistence of biofilms in general (38). Phase variation is the mechanism by which many of these different phenotypes are produced. This mutationally generated phenotype switch is reversible and inheritable. Genetic rearrangements are capable of causing a change in phenotype and are often the means through which a microbe switches phenotype, either within a cellular genome or through MGEs acting between cells (28, 33).

Minimal Model for Mobile Genetic Element Mediated Phase Variation

To model phase variation mediated by horizontal gene transfer, our strategy is to extract the features common to all of the molecular mechanisms of genome rearrangement described above, as is described in refs. 39 and 40, even though we fully recognize that there are specific case-by-case variations. The end result of any gene transfer mechanism is the simple transfer of genes between cells. Particulars may differ, but the main effects are the same. In each of these systems, there is at least one actively expressed locus that is responsible for phenotype. Changes in the genetic material at this locus result in a change in phenotype or phase variation. In addition, there is usually a means of preserving the inactive genetic material. For example, in the case of intragenomic recombination, inactive genetic material in the form of partial copies of a gene was stored in several unexpressed storage loci (20).

Because these shared general features are likely to exist in some way in a broad class of genetically mediated phase variation systems, we can construct a generic minimal model for describing the main features of all MGE-mediated phase variation systems. In this model exist two phenotypes labeled 0 and 1. There are two types of gene, 0 and 1, each corresponding to a phenotype. A microbial cell contains a genome with two genes in two loci: an active expressed locus gene α and an inactive storage locus gene β. The phenotype of a given microbe is given by the gene in the active locus. The gene at the storage locus has no effect on the phenotype of the microbial cell. We denote the four possible microbial genome types by the indices αβ. The first index denotes the gene at the active locus while that second index denotes the gene in the storage locus. The four different possible microbial genomes are in this notation: 00, 01, 10, and 11. ψ_αβ denotes the number of microbes with genome αβ. The first two types of microbes, ψ₀₀ and ψ₀₁, express the 0 phenotype, while the last two, ψ₁₀ and ψ₁₁, express the 1 phenotype. The composition of the microbial community is represented by the relative abundances of each of the four microbial genomes.

The microbes within the community are capable of interacting with the MGEs of the community. An individual microbe may take in an external gene x from the shared gene pool of the community. That gene can recombine with the active locus with a certain probability q_x or with the storage locus with a probability 1 − q_x. The site-specific probability of recombination depends on the type of gene that enters the microbe. The external gene comes from a community gene pool whose composition is a direct reflection of the composition of the cellular genomes. In other words, the chance of getting a 0 gene is p₀ = (2ψ₀₀ + ψ₀₁ + ψ₁₀)/(2 ψ_total), where ψ_total = ψ₀₀ + ψ₀₁ + ψ₁₀ + ψ₁₁. Conversely, the probability of getting a 1 gene is 1 − p₀.

Phase variation, or phenotype switching, occurs when the active locus in a genome is overwritten with a gene for a different phenotype. For example, if a 1 gene enters into a microbe with a 00 genome and overwrites the active locus subsequently transforming it into a 10 genome, then that microbe has undergone a switch from a 0 phenotype microbe to a 1 phenotype microbe.

One of the common and important features of biofilms and phase variation is the emergence of a steady-state ratio of phenotypes after the culture reaches stationary state. This is no doubt important for preserving variety, i.e., preventing all cell types from switching to variant types, and enforcing some advantageous fractions of coexistence between phenotypes. Because different phenotypes play different roles within a microbial community, there is a particular ratio of role players that is most efficient and effective for the maintenance, survival, growth, and dispersal of the biofilm.

To understand the steady state ratio of phenotypes, we normalize the total number of microbes so that ψ_total = 1. ψ_αβ then gives the fraction of the population with the genome αβ. Because our purpose is to examine the stationary state, we do not allow cellular growth or death. Only gene transfers drive the system. The two parameters of this system are q₀ and q₁, the probabilities of each type of gene recombining with the active locus. The time-dependent dynamics of the system are then given by the equation

where r is the rate of intercellular horizontal gene transfer. The terms in these equations describe, within mean-field theory, the processes of gene transfer; for example, the probability of going from a 00 genome to a 10 genome depends on the probability of obtaining a 1 gene from the gene pool p₁ and having that gene recombine with the active site q₁. This particular sequence of events carries a total probability of p₁q₁ = (1−p₀) q₁. Although these equations can be derived as moments from a master equation formalism, we expect that in a biofilm environment, fluctuations are small, and the mean field approximation is reliable. The steady state is then given by the fixed point transfer matrix equation

where Ψ is a vector whose components are ψ₀₀, ψ₀₁, ψ₁₀, and ψ₁₁, and T̂ is a transfer matrix

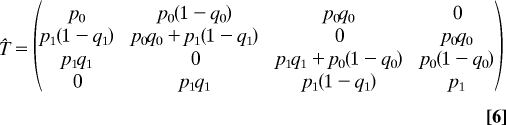whose elements describe the transition probabilities given a gene pool matching the composition of the cells. This steady state condition can be derived from the time-dependent equations, because all transition probabilities must sum to unity.

Results

Steady States.

Stable steady state solutions for Eq. 1 with coexisting phenotypes only exist for the conditions 0 < q_x < ½ and ½ < q_y < 1 where (x, y) are (0, 1) or (1, 0). In other words, each gene must have a different primary site for recombination. Otherwise the resulting competition leads to the eventual fixation of one gene to the exclusion of the other, and no stable coexistence can occur. The coexisting fraction of 0 phenotype microbes ρ₀ can be found by solving Eq. 1, yielding

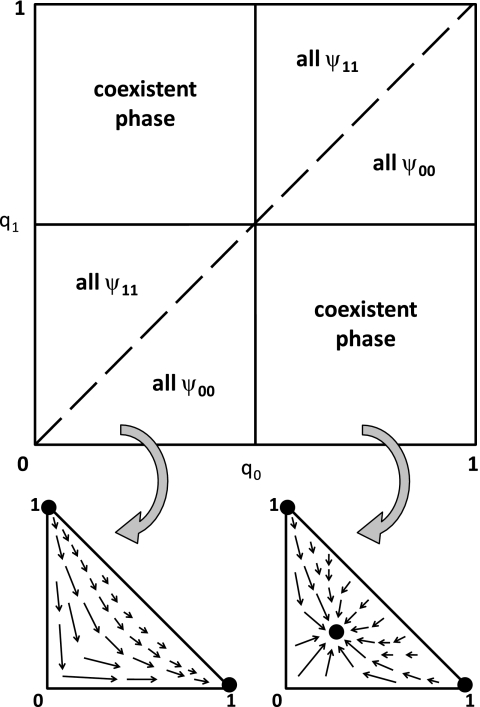
This equation describes the steady state coexistence for the zero growth and equal transfer rates for both types of genes. For 0 < q_x < q_y < ½ or ½ < q_y < q_x < 1, gene x saturates all loci in the system completely excluding gene y. Also, 0 < q₀ = q₁ < 1 results in an unstable equilibrium. Fig. 1 shows the phase diagram and a diagrammatic representation of the stability of the fixed points in both the single and coexistent phenotype phases. In the singular phase, the population fractions flow toward all 00- or 11-genotypes and away from any intermediate values. The coexistent phase is characterized by an attractive fixed point given by the solution to Eq. 1. For example, the fixed point drawn in Fig. 1 would be given by

Fig. 1.

Phase diagram and flows for a two-phenotype model of a biofilm. (Upper) Phase diagram showing two distinct phases. One phase consists only of a single genotype, either 00 or 11, and thus only one phenotype. The other phase is characterized by the stable coexistence of both phenotypes and called the coexistent phase. The solid lines represent phase boundaries while the dashed line denotes the separatrix between the phenotypes in the single-phenotype phase. The separatrix is a point of unstable equilibrium, where coexistence of phenotypes is in principle possible but practically impossible, being unstable to any perturbations or fluctuations in the dynamics. (Lower) Schematic flow diagram in both the single phenotype regime (Left) and the coexistent regime (Right) projected onto the ψ₀₀–ψ₁₁ plane. Note that in the single phenotype regime, the system dynamics tends to flow toward either all 00-genotypes (ψ₀₀ = 1) or all 11-genotypes (ψ₁₁ = 1). In the coexistent phenotype phase, the phase flows toward genotype fractions given by Eq. 4 and away from unstable fixed points at ψ₀₀ = 1 and ψ₁₁ = 1.

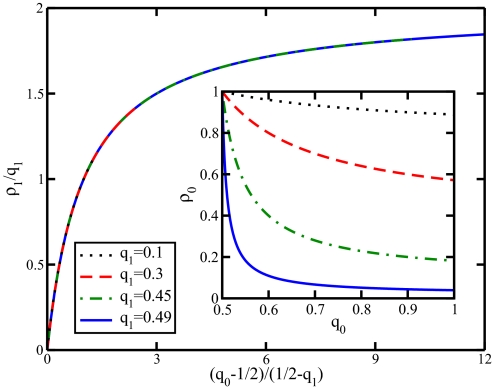
In Fig. 2, we show how the phenotype fraction varies with q₀ and q₁, exhibiting the way in which the family of curves conveniently collapse onto a universal curve when plotted in the manner specified by Eq. 1.

Fig. 2.

A rescaled plot of the fraction of 1 microbes (1 − ρ₀) = ρ₁ as a function of q₀ for fixed values of q₁ given by Eq. 1. (Inset) The same data using the original axes ρ₀ versus q₀. q₀ and q₁ represent the probability for a horizontally transferred 0 or 1 gene, respectively, to recombine with the expression locus rather than the storage locus. For stable coexistence, q₀ and q₁ are subject to the constraints 0 < q_x < ½ and ½ < q_y <1, where (x, y) are either (0, 1) or (1, 0).

Dynamics.

We have shown how stable coexistence of two phenotypes can arise via the mechanism of gene transfer. In this section, we wish to further examine the dynamics of gene transfer for changing populations of microbes. Thus, we will consider the role of both initial conditions and microbial growth.

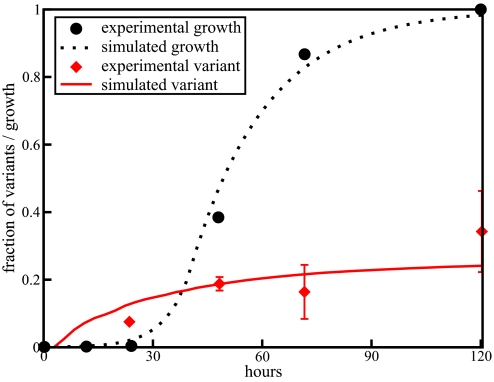
Consider the onset of variant phenotypes in biofilm cultures. Although natural biofilms can comprise, with attendant genetic exchanges, a variety of microbial types, their phenotypic behavior can be conveniently studied using a single organismal strain. Typically, a biofilm reactor is inoculated with cells from a planktonic batch culture that consists almost entirely of one phenotype, the so-called typical or wildtype phenotype. We can simulate this experiment by initializing a microbial population with microbes of one phenotype. The genotypes of these microbes are assigned according to the fraction of the genotypes for that phenotype in steady state given by solving Eq. 1 for ψ₀₀ and ψ₀₁. These microbes are then allowed to grow and undergo gene exchange. The doubling times for different phenotypes of P. aeruginosa were experimentally measured and found to be comparable (3, 38). Thus, we use equal growth rates for both phenotypes. Gene exchange occurs according to the same rules as the static case as given by Eq. 3 with q₀ = 0.53 and q₁ = 0.47. The rate of gene exchange, ¾ per cell per generation, is obtained by fitting the simulation results to the experimentally measured variant phenotype fractions. Because the growth rate, q₀, and q₁ are fitted to experimental data, the gene transfer rate is the only remaining free parameter [for more details on how the simulation results were generated, see supporting information (SI) Text]. This leads to a predicted value for the gene transfer rate that is commensurate with recent experimental results obtained by direct visualization of plasmid transfer between bacterial cells and subsequent integration into the genome (41). Fig. 3 shows our prediction for the growth and onset of a variant phenotype compared with data from Boles et al. for the mini variant (38). The parameters q₀ and q₁ were determined by fitting Eq. 1 to the stationary growth phase steady state fraction of the variant phenotype.

Fig. 3.

Plot of biofilm growth and development of variant phenotypes. The simulation results were scaled to fit the experimental growth data from Boles et al. (38). The rate of gene exchange is 3/4 per cell per replication time in the exponential growth phase. The constants governing the probabilities of recombination locale for each gene are q₀ = 0.53 and q₁ = 0.47. The initial population size in the simulation is 10³ and the final population size is 10⁶. The initial experimental population of 10⁵ grows to 10⁸ over the course of the experiment.

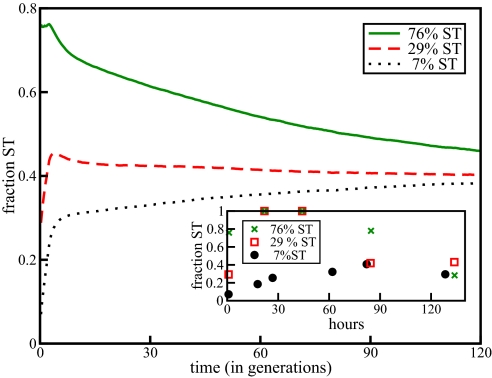
Next, consider the effects of different initial populations. In another recent experiment, Kirisits et al. (3) isolated WT and sticky (ST) variants of P. aeruginosa. They then inoculated cultures using three different ratios of WT to ST, 93:7, 71:29, and 24:76 and allowed them to grow. This differs from the described experiment by Boles et al. (38), which only considered cultured innoculated with a typical to variant ratio of 1:0. Again, we can simulate this by initializing our simulation with different ratios of WT to ST, with genotypes taken according to their steady state distributions. Although the doubling times may be similar between the two phenotypes, we now take into account the enhanced ability of the ST variant to attach to both surfaces and other microbes by altering the effective growth rates in slight favor of the ST variant. This represents the observed fact that ST variants are prone to losing less cells to the effluent and that they in general are better at adhering to other objects. Fig. 4 shows qualitative agreement between experiment and our simulation. Specifically, we can reproduce the initial “hump” from the experimental results.

Fig. 4.

Plot of simulated coculture experiment with various ratios of WT to ST. Total population in the simulation began as 10⁴ and grew to 10⁶. The effective WT growth rate is 15% less then the effective ST growth rate. This represents the enhanced ability of the ST type to adhere. The other parameters are the same as for Fig. 4. (Inset) Experimental results from Kirisits et al. (3). The total experimental population went from 10⁶ to 10⁸.

Discussion

In this article, we proposed a generalized MGE-mediated mechanism through which the individual microbes in a biofilm community interact. The relatively high cell density of a biofilm assists this mechanism, and leads to a collective model of phase variation whose dynamics can be readily calculated and compared with experimental data, as shown in Figs. 3 and 4.

It is important to note that our theory captures many of the experimentally observed elements of phase variation, without invoking detailed molecular mechanisms or many fitting parameters. Instead, our approach only needs to incorporate general features of gene exchange and recombination, so that we may appropriately refer to it as a “minimal model.” Our theory contrasts with epigenetic mechanisms (26), which generally operate on a time scale too fast to be relevant for phenotype variation. Recombination-independent mutations, such as slip strand mutations on simple sequence repeats, also cause phase variation (42), but these purely internal mechanisms differ from the collective dynamic we present.

We turn now to some comments that compare and contrast the implications of our work for biofilms and planktonic batch cultures. The fraction of variant phenotypes in laboratory-grown planktonic batch cultures that are clonal is generally found to be small or non-existent (3, 28, 38). This is expected in our model, because the rate of gene transfer between cells in planktonic batch culture would most likely be far lower then the rate of transfer in biofilms, an expectation that is consistent with reported comparisons between electron micrographs of cells of Salmonella typhimurium grown in biofilm and planktonic batch culture (9). With their lower cell density, planktonic batch cells would be less influenced by the MGE-mediated exchange. If typical or WT held even a slight advantage in planktonic batch culture, they could possibly outgrow the much slower rate of variant formation. Attachment-enhanced phenotypes may incur a higher metabolic cost that essentially goes wasted in a planktonic batch culture. Any properties that give a relative advantage to typical gene insertion at the active loci also provides a method for affecting a low number of variant types in clonal planktonic batch culture.

In natural environments, genetic variety is the rule rather then the exception (43, 44), whether microbial populations exist in the planktonic or biofilm state. A gene exchange mechanism for phenotype switching would perforce imply a greater phenotypic diversity in natural systems than in planktonic batch laboratory strains that are clonal, because of the larger number of gene types being exchanged in natural environments and the wider variety of microbial genomes present. Realistically, MGEs would interact with and affect many different loci in many different genomes, and the interactions between these elements would result in a combinatorial increase in variety. In principle, our model can be extended to describe more complex microbial communities than the simple one treated here.

Conclusion

In this article, we have proposed a model for phase variation in biofilms, which demonstrates that collective interactions can lead to the emergence of population structure. The model predicts the stable coexistence of two different phenotypes in biofilms, and reproduces the population dynamics seen in experiments on the formation of variants in biofilm cultures. Insight into phase variation and other collective phenomena has broad implications for our understanding of bacterial pathogens, microbial ecology, and evolution.