Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2008 Jul 25;95(9):4266–4276. doi: 10.1529/biophysj.108.138271

Trans-Channel Interactions in Batrachotoxin-Modified Rat Skeletal Muscle Sodium Channels: Kinetic Analysis of Mutual Inhibition between μ-Conotoxin GIIIA Derivatives and Amine Blockers

Quanli Ma 1, Evgeny Pavlov 1, Tatiana Britvina 1, Gerald W Zamponi 1, Robert J French 1
PMCID: PMC2567937  PMID: 18658223

Abstract

R13X derivatives of μ-conotoxin GIIIA bind externally to single sodium channels and block current incompletely with mean “blocked” durations of several seconds. We studied interactions between two classes of blockers (μ-conotoxins and amines) by steady state, kinetic analysis of block of BTX-modified Na channels in planar bilayers. The amines cause all-or-none block at a site internal to the selectivity filter. TPrA and DEA block single Na channels with very different kinetics. TPrA induces discrete, all-or-none, blocked events (mean blocked durations, ∼100 ms), whereas DEA produces a concentration-dependent reduction of the apparent single channel amplitude (“fast” block). These distinct modes of action allow simultaneous evaluation of block by TPrA and DEA, showing a classical, competitive interaction between them. The apparent affinity of TPrA decreases with increasing [DEA], based on a decrease in the association rate for TPrA. When an R13X μ-conotoxin derivative and one of the amines are applied simultaneously on opposite sides of the membrane, a mutually inhibitory interaction is observed. Dissociation constants, at +50 mV, for TPrA (∼4 mM) and DEA (∼30 mM) increase by ∼20%–50% when R13E (nominal net charge, +4) or R13Q (+5) is bound. Analysis of the slow blocking kinetics for the two toxin derivatives showed comparable decreases in affinity of the μ-conotoxins in the presence of an amine. Although this mutual inhibition seems to be qualitatively consistent with an electrostatic interaction across the selectivity filter, quantitative considerations raise questions about the mechanistic details of the interaction.

INTRODUCTION

In voltage-gated calcium (CaV) and potassium (KV) channels, repulsive interactions among ions within a single channel seem to be a fundamental determinant of channel conductance and selectivity (1–5). In KV channels, interactions are reflected in dramatic coupling between uni-directional fluxes (6–8), the modulation of the action of blockers by permeant ions (9,10), and interactions of blockers binding from opposite sides of the channel. In general, interactions are more subtle in voltage-gated sodium (NaV) channels. Flux coupling, although measurable, is much weaker (11,12), and binding of conducting ions suggests a considerably lower affinity (13,14) than for some sites in KV channels (15). Nonetheless, ionic interactions are important contributors to NaV channel behavior. Competitive interactions between sodium and calcium, significantly affect the shape the sodium current-voltage relation, and the amplitude of the current under physiological ionic conditions, especially at voltages near the normal firing threshold for action potentials (14,16). Overall, the NaV channel data suggest that double occupancy, and concomitant ionic interactions, can occur in sodium channels, but that they do so with a relatively low probability compared with KV and CaV channels. Interactions within NaV channels may also modulate actions of drugs (17) and toxins (18). In this study, we examine the interactions between two classes of sodium channel ligands, which block the channel from opposite ends.

μ-Conotoxin GIIIA is a rigid, 22-amino acid peptide toxin, which causes long, all-or-none blocking events when it binds to the extracellular end of single, skeletal muscle, sodium channels (19,20). R13Q and R13E derivatives of μ-conotoxin GIIIA cause incomplete slow block of the sodium channel (21–23). In the case of R13Q (nominal net charge, +5), residual conductance is ∼30% of unblocked single-channel conductance, and in case of R13E (nominal net charge, +4), residual conductance is ∼50%. Amines (TPrA and DEA) cause all-or-none block from cytoplasmic side at a site internal to the selectivity filter, presumably the local anesthetic receptor, or at least part of it. TPrA and DEA cause two different modalities of single-channel blockade. TPrA induces moderately rapid, discrete, interruptions of current (17); qualitatively similar results were obtained for tetra-butyl ammonium in patch clamp studies on cardiac sodium channels (24). DEA, in contrast, causes a reduction of the apparent single-channel amplitude (17,25), similar to that seen for tetra-ethyl ammonium (24,26).

In our studies, we use pretreatment with BTX to allow steady-state recordings of amine and toxin block. BTX offers unique advantages for these experiments, which outweigh the disadvantages of working with a modified channel. A key feature is the almost complete elimination of inactivation, allowing analysis of blocking interactions in extended steady-state recordings. Although BTX modification changes quantitative details (unitary conductance, selectivity, gating), numerous, defining qualitative features of channel behavior are retained by BTX-treated channels, including: 1), Na selectivity, albeit reduced (27–31); 2), interactions with amines, e.g., heart isoform selectivity of lidocaine block (32); 3), partial block by selected μ-conotoxin derivatives (21); and 4), instantly reversible shifts of activation gating on conotoxin binding and dissociation (21).

Block by either TPrA or DEA is easily distinguished from the long duration (s), partial interruptions in the single channel current produced by binding of the conotoxin derivatives. This enables direct analysis of trans-channel interactions between these two classes of blockers (toxins and amines), from single-channel records for which both agents are present. Kinetic analysis is thus a powerful tool to explore the interactions between these two types of sodium channel ligands. On this basis, we describe a mutual inhibition between toxin and amine blockers, which bind from opposite ends of the channel.

MATERIALS AND METHODS

Peptide synthesis

Peptide synthesis has been described in detail (22). In brief, linear peptides were produced by solid phase synthesis using 9-fluorenylmethoxycarbonyl (Fmoc) chemistry by Dr. Denis McMaster (Peptides Services, Faculty of Medicine, University of Calgary). Coupling of Fmoc amino acids was carried out using the HBTU/HOBT/DIPEA method on an Applied Biosystems 431A synthesizer (Applied Biosystems, Foster City, CA). The raw peptides were air oxidized and purified as described (33). During oxidation, cyclization was monitored by analytical HPLC and usually complete after 2–3 days at 4°C. After folding of the peptide by air oxidation, toxin derivatives were purified to near homogeneity by HPLC (∼95%, based on analytical HPLC). Active toxin derivatives were isolated as a single major peak. The identity of purified peptides was confirmed by quantitative amino acid analysis and, in some cases, by electrospray mass spectroscopy molecular weight determination. As a check that the folded structures did not deviate qualitatively from that of the native toxin, one-dimensional proton NMR spectra were recorded at 15°C in aqueous solution containing 5% D2O at 500 MHz. The proton chemical shifts of the R13X derivatives were generally similar to those for the native toxin.

Membrane vesicle preparation and bilayer setup

Sodium channel-containing plasmalemmal vesicles were isolated as described before (20), sonicated and incubated with 500 nM BTX in a 0.3 M sucrose, 20 mM HEPES solution (pH 7.4), and kept at +4°C, for at least 1 day before use, to inhibit both fast and slow channel inactivation (28). The predominant sodium channel isoform is presumed to be rNaV1.4; this is consistent with experiments in which μCTX block assayed using whole cell recordings from cells expressing rNaV1.4 was compared with results from single-channel recording in bilayers (21). One to five microliters of incubated vesicles was pipetted into one well of a bilayer chamber containing a bathing solution of 200 mM NaCl (EM Science, Gibbstown, NJ), 10 mM MOPS (Sigma-Aldrich, Oakville, Ontario, Canada), 0.1 mM Na2EDTA (Sigma-Aldrich), pH 7 (NaOH; BDH from VWR International, Edmonton, Alberta, Canada) in both wells. Bilayers were formed from a 4:1 mixture of phosphatidylethanolamine and phosphatidylcholine (both from Avanti Polar Lipids, Alabaster, AL) dissolved in decane (Fisher Scientific, Ottawa, Ontario, Canada) before vesicle injection. Saturated 3 M KCl salt bridges linked the bathing solutions in each well to a 3-M KCl reservoir with which contact was made by way of Ag/AgCl electrodes. Recordings were carried out at room temperature (≈22°C).

Data acquisition

After incorporation, channel orientation was determined from its voltage-dependence of gating. Current measurements were taken with an Axopatch-1B patch-amplifier (Bessel filtered at 100 Hz, 80 dB/decade; Molecular Devices), digitized with a NeuroCorder DR-284S digitizer (Neuro Data Instruments, New York, NY), 8-pole low-pass Bessel filtered at 100 Hz (−3 dB; model 902LPF; Frequency Devices, Haverhill, MA), monitored on a digital oscilloscope (Nicolet Instrument model 2090-IIIA), and recorded onto videotape. Data were transcribed onto a computer during the recording or through the videotape, sampled at 1 kHz (Fetchex 5.5.1 acquisition software driving an Axolab I digital interface; Molecular Devices).

Single-channel event recognition and analysis

These experiments involved long recordings (∼0.5–2.5 h) of single Na channels exposed to the following blockers: R13E, R13Q, TPrA, and DEA. After addition of a particular concentration of a blocker that induced discrete events, channel activity was recorded continuously for a time sufficient to collect ∼200 events when possible. Then, the next concentration of blocker was added, channel activity was recorded, and the process repeated, until the bilayer broke.

The long conotoxin-bound periods are easily distinguished by eye, allowing these periods to be cursor selected, and the events representing the much faster amine block of the toxin-bound, or of the toxin-free channel to be separately analyzed. For convenience, conotoxin concentrations were chosen to give a probability of the channel being toxin-bound of ∼0.5. See Figs. 2 and 5, for records at different amine concentrations. Also, in the companion article by Pavlov et al. (34), Figs. 1 and 2, show amine block at a range of different voltages.

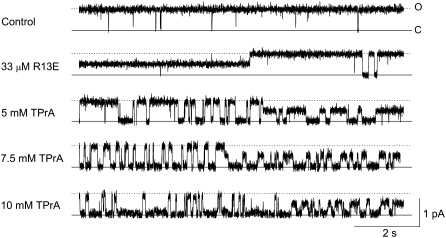
FIGURE 2.

FIGURE 2

Open in a new tab

Block of a single sodium channel by TPrA. [TprA] dependence in periods where the channel is R13E-bound, or R13E-free. Current traces were recorded from a single BTX-activated, rat skeletal muscle sodium channel under control conditions (top trace: symmetrical 200 mM NaCl, 10 mM MOPS, pH 7.0), and after addition of 33 μM external R13E (second trace), and then with the further addition of 5, 7.5, or 10 mM internal TPrA (bottom three traces). The holding voltage in this and all other experiments is +50 mV. Solid lines indicate the closed level (C), and dotted lines indicate the open (O) level (R13E unbound). The long segments showing the channel opening to an intermediate level represent periods during which R13E is bound, partially blocking current through the channel. These events are seen in the first part of the second trace, and the latter sections of the bottom three traces.

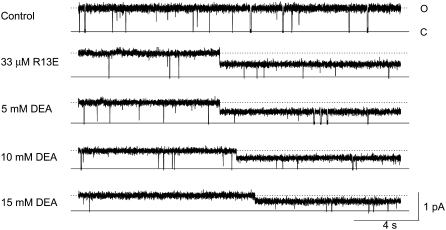
FIGURE 5.

FIGURE 5

Open in a new tab

Concentration dependence of DEA block of single sodium channels, when either bound or unbound by R13E. Current traces recorded from a single BTX-activated rat skeletal muscle sodium channel under control conditions (symmetrical 200 mM NaCl, 10 mM MOPS, pH 7.0), and after addition of 33 μM external R13E, then with the further addition of 5, 10, or 15 mM internal DEA. The holding voltage in this and all other experiments is +50 mV. Solid lines indicate the closed level (C), and, for reference, the dotted lines approximate the open (O) level (R13E not bound).

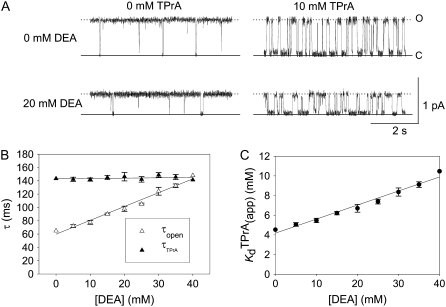
FIGURE 1.

FIGURE 1

Open in a new tab

Competitive interaction between TPrA and DEA. (A) Dependence of TPrA block on [DEA]. Current traces recorded from a single BTX-activated rat skeletal muscle sodium channel under control conditions (symmetrical 200 mM NaCl, 10 mM MOPS, pH 7.0). The upper left trace was obtained under control conditions, and the upper right was recorded in the presence of 10 mM TPrA alone. The lower left trace was obtained in the presence of 20 mM DEA alone, the lower right trace was taken in the presence of both 10 mM TPrA and 20 mM DEA. The holding voltage in this and all other experiments is +50 mV. Solid lines indicate the closed level (C), and dotted lines, the open (O) channel level. (B) Mean dwell times for TPrA-block (τTPrA, ▴) and TPrA-unblock (τopen, Δ) as a function of [DEA]. 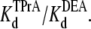(C) Calculated apparent dissociation constant for TPrA, Inline graphic(app), as a function of [DEA], determined as described in Materials and Methods. The intercept represents Inline graphic at = 50 mV at 0 mM [DEA]. The slope is Inline graphic Data points and error bars in B and C are the mean ± SE for one to three different single Na channels at each concentration of DEA. Concentration of TPrA is 10 mM.

Events representing R13E-blocked, R13Q-blocked, TPrA-blocked, or unblocked states were identified using a detection threshold of 50% of the appropriate transition amplitude. Lifetimes were generally measured from populations of dwell times (n > 100 events) that were binned, plotted as probability density functions (e.g., see Fig. 8), and fit to a single exponential function of time using the approach of Sigworth and Sine (35), as implemented in pCLAMP analysis software from Molecular Devices.

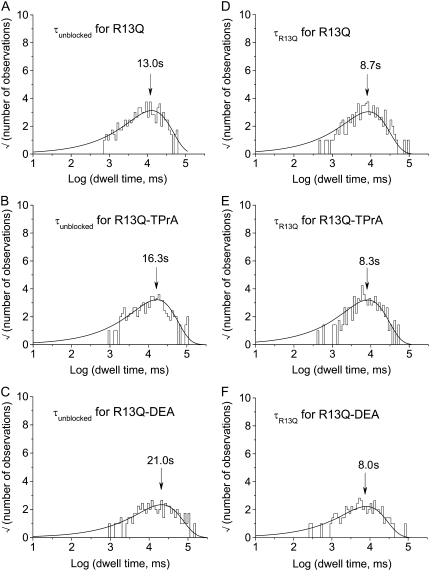
FIGURE 8.

FIGURE 8

Open in a new tab

Probability density histograms of R13Q-blocked events recorded in the absence and presence of amines. The sampled events were binned and plotted using the square root versus log time format of Sigworth and Sine (see Materials and Methods). Arrows indicate the time constants. (A) Unblocked dwell times recorded from single Na channels in the presence of 8 μM external R13Q. Unblocked events from six different single Na channels were pooled to obtain a sample of 225 events. The solid line is a fit of the data to a single exponential with a time constant of 13.0 s. (B) Unblocked dwell times recorded from single Na channels in the presence of 8 μM external R13Q and 10 mM internal TPrA. Unblocked events from four different single Na channels were pooled to obtain a sample of 214 events. The solid line is a fit of the data to a single exponential with a time constant of 16.3 s. (C) Unblocked dwell times recorded from single Na channels in the presence of 8 μM external R13Q and 10 mM internal DEA. Unblocked events from five different single Na channels were pooled to obtain a sample of 123 events. The solid line is a fit of the data to a single exponential with a time constant of 21.0 s. (D) Blocked dwell times recorded from single Na channels in the presence of 8 μM external R13Q. Blocked events from six different single Na channels were pooled to obtain a sample of 224 events. The solid line is a fit of the data using a single exponential with a time constant of 8.7 s. (E) Blocked dwell times recorded from single Na channels in the presence of 8 μM external R13Q and 10 mM internal TPrA. Blocked events from four different single Na channels were pooled to obtain a sample of 216 events. The solid line is a fit of the data using a single exponential with a time constant of 8.3 s. (F) Blocked dwell times recorded from single Na channels in the presence of 8 μM external R13Q and 10 mM internal DEA. Blocked events from five different single Na channels were pooled to obtain a sample of 123 events. The solid line is a fit of the data using a single exponential with a time constant of 8.0 s.

Single-channel block by internal DEA was manifested as a “fast block” corresponding to an apparent decrease in unitary current (13). Unitary current as a function of [DEA] was measured with the use of all-points amplitude histograms to determine the mean value of the closed and apparent open state current levels. Note that the dependence of apparent unitary current amplitude on [DEA] is consistent with very rapid (undetectably fast) all-or-none block, as described (25). This is quite distinct from the discrete, long-duration, partial block resulting from binding of the R13X conotoxins. In that case, the amplitude of current through the toxin-bound state is independent of toxin concentration, and shows only a slight rectification as a function of voltage (20–22).

Nonlinear curve fitting to various equations was carried out using Sigma Plot software (SPSS, Chicago, IL).

Contribution of spontaneous closures and missed events to the estimates of kinetic parameters for TPrA block

The identification of dwell times in closed, TPrA-blocked, and toxin-bound states is facilitated by the fact the mean durations of these events differ by ∼100-fold, from closed to TPrA blocked, and from TPrA-blocked to toxin-bound. Open and blocked times in the presence of TPrA were measured from raw current traces without exclusion of any events. The fraction of events missed due to the filtering (fmiss) were estimated from the following (36):

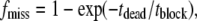graphic file with name M4.gif

where tdead, defined as a duration of missed events, tdead = 0.179/fc; fc = 100 Hz, filtering corner frequency, −3 dB (37). Considering a mean tblock measured from dwell-time histogram of 166 ms, the predicted fraction of missed short TPrA blocking events is fmiss = 0.01. Another possible source of systematic error arises from channel closures due to spontaneous gating, which, in our analysis, could be misinterpreted as TPrA blocking events. Based on the kinetic analysis of spontaneous channel closures (tclosed = 5 ± 3 s; topen = 96 ± 87 ms; mean ± SD), we estimate that maximal contribution (at the lowest TPrA concentration used) of these closures to the measurements of topen TPrA were ∼4% (in other words ∼4% of interruptions in open times were caused by spontaneous closures, rather than by TPrA binding). Channel open probability in the absence of TPrA was ∼0.98. Taking into account that the contribution of spontaneous closures would be similar for TPrA block of the toxin-free, and the toxin-bound state of the channel their contribution to the estimated change in TPrA Kd between the toxin-free and toxin-bound channel was minimal, and considered insignificant. A further check is provided by comparing estimates of Kd from the binding and dissociation rate constants with those from the fractional block estimated arithmetically from the number of points in the current record above and the standard 50% detection threshold for open-closed/blocked transitions. These two approaches yield similar trends for changes in probability of TPrA block associated with binding of toxin. (See Results for comparison of Kd calculations based on kinetics and open probabilities.) Finally, the probability of missed “silent” binding of the toxin defined as toxin binding-dissociation during TPrA blocking event was <0.3%.

Kinetic analysis of amine block

Steady state and kinetic parameters were determined from the open and blocked time distributions using the following standard relationships:

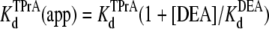graphic file with name M5.gif (1)
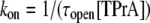graphic file with name M6.gif (2)
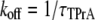graphic file with name M7.gif (3)
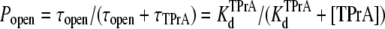graphic file with name M8.gif (4)
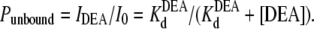graphic file with name M9.gif (5)

In the above equations, the symbols are as follows: τTPrA, mean life time for TPrA-block; τopen, mean open time, which approximately equals the mean time between TPrA-block events; kon, association rate constant for TPrA; koff, dissociation rate constant for TPrA; 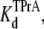Inline graphic equilibrium dissociation constant for TPrA; Popen, time-averaged probability of the TPrA unblock state; Punbound, channel's probability of unblocked by DEA; I0, single channel current in the absence of DEA; IDEA, residual single channel current in the presence of DEA; 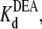Inline graphic equilibrium dissociation constant for DEA. 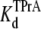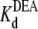(Strictly speaking, the equilibrium dissociation constants, Inline graphic and Inline graphic also are “apparent” values, appropriate to the conditions of the experiments, including [Na+], pH, and so on.)

RESULTS

DEA and TPrA compete for the inner vestibule

DEA and TPrA are both small blockers that enter sodium channels from the cytoplasmic end and bind to a site internal to the selectivity filter. However, DEA and TPrA cause two different kinetic modes of single-channel blockade: reduction of the apparent single-channel amplitude (DEA), and discrete, all-or-none interruptions of current (TPrA) as described (17). Fig. 1 A shows the typical recordings of TPrA-block (upper right) and DEA-block (lower left), and the combined action of the two amines, simultaneously present (lower right). The different characteristics of block enable analysis of interaction between the two internal blockers from one set of single-channel records. We measured the dwell times for TPrA-block (τTPrA) or TPrA-unblock (τopen) in the presence of 10 mM TPrA and different concentrations of DEA (0–40 mM). For a system that adheres to a single-site competition mechanism (38), the dwell time of the TPrA-block (τTPrA) is expected to be independent of DEA concentration. In contrast, the dwell time of TPrA-unblock (τopen) is expected to increase with DEA concentration. Consistent with these predictions, Fig. 1 B illustrates that τopen increases linearly with increasing [DEA], whereas τTPrA is constant. Fig. 1 C shows the apparent calculated 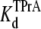Inline graphic(app) increases with increasing [DEA]. According to the one-site competition mechanism, Fig. 1 C could be predicted by Eq. 1 and 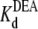Inline graphic can be estimated from the slope of the line (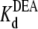Inline graphic = 29.1 mM). 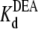This calculated Inline graphic is consistent with the earlier work on rat skeletal muscle sodium channels (25), Inline graphic = 27.0 mM. Other studies on both bovine cardiac and rat skeletal muscle channels suggested a 1:1 interaction between the channel and the various amines (17,21). Our results support this suggestion, and further indicate that DEA and TPrA compete for the same binding site in the channel.

R13X conotoxins binding decreases the affinity for TPrA

TPrA blocks Na channel and causes discrete blocked events from internal side. R13X blocks Na channel from external side. To study the trans-channel interaction between TPrA and R13X, we measured the kinetics of TPrA when R13X bound or unbound the sodium channel from external side.

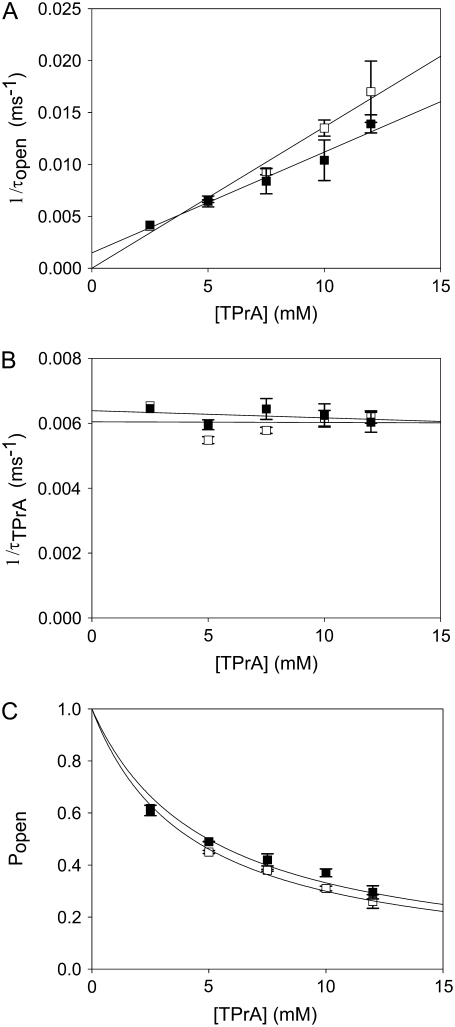
Fig. 2 shows typical results from an experiment in which current through a single Na channel was recorded in the presence of 33 μM R13E, and then during consecutive exposure to 5, 7.5, and 10 mM internal TPrA. These records show that R13E-block is incomplete, and the residual current is ∼50%. For R13Q, the residual current is ∼30% (not shown here; see previous reports (20,22)). The records also show that the channel's open/unblocked probability decreases with TPrA concentration. The association rate constants for TPrA, kon, for binding to a R13E-free or R13E-bound channel, were calculated according to Eq. 2. The mean lifetime of τopen measured for three different single channels at each TPrA concentration is plotted in Fig. 3 A and fit to Eq. 2. This fit gives an estimate of kon = 1.36 ± 0.10 × 103 s−1M−1 for R13E-free channel, and kon = 0.97 ± 0.09 × 103 s−1M−1 for R13E-bound channel. The difference between the two kon for TPrA when R13E free and R13E bound is considered by t-test to be statistically significant difference (p = 0.0002). The dissociation rate constant, koff, calculated according to Eq. 3 from the reciprocal of the mean of five τTPrA measurements in Fig. 3 B is koff = 6.03 ± 0.41 s−1 for R13E-free channel, koff = 6.22 ± 0.23 s−1 for R13E-bound channel. The two estimates of koff are not statistically different (p = 0.3925). The kinetic ratio, koff/kon, or Kd, is the equilibrium dissociation constant for TPrA. 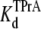Inline graphic = 4.43 ± 0.44 × 10−3 M (R13E-free, c.f. Fig. 1 C intercept, determined from TprA/DEA competition), and 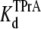Inline graphic = 6.41 ± 0.64 ×10−3 M (R13E-bound). The 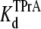Inline graphic equilibrium constant can also be estimated from the time-averaged probability of the TPrA unblock state, Popen. Fits of the data in Fig. 3 C to Eq. 4 yield 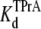Inline graphic = 4.27 ± 0.11 × 10−3 M (R13E-free), and 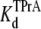Inline graphic = 4.96 ± 0.34 × 10−3 M (R13E-bound), in agreement with the kinetic ratio of koff/kon. These data indicate that bound R13E slows TPrA association, but does not effect the TPrA dissociation rate. R13E blocked the channel from external side causes 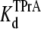Inline graphic to increase significantly (p = 0.0026), and the affinity for TPrA binding to the R13E-blocked channel is weaker than that for the unblocked channel.

FIGURE 3.

FIGURE 3

Open in a new tab

Kinetic analysis for TPrA in the presence of R13E. (A) The reciprocal of open/unblocked time of TPrA (τopen) as a function of TPrA concentration. (B) The reciprocal of closed/blocked time of TPrA (τTPrA) as a function of TPrA concentration. (C) Measured probability that the channel is not occupied by TPrA (Popen) as a function of [TPrA]. Data points and error bars in A–C are the mean ± SD for three to four different single Na channels at each concentration of TPrA. (□) Data when channel was not bound by R13E from extracellular side; (▪) data when channel was bound by R13E from extracellular side. The solid lines in A are fits to Eq. 2, used to measure the association rate constants, kon. The solid lines in B are linear fits to the means of five determinations the dissociation rate constants, koff (Eq. 3) at each [TPrA]. The solid lines in C are fit to Eq. 4 to measure the equilibrium dissociation constants 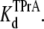Inline graphic Asterisks (*) denote a significant difference (t-test, p < 0.05).

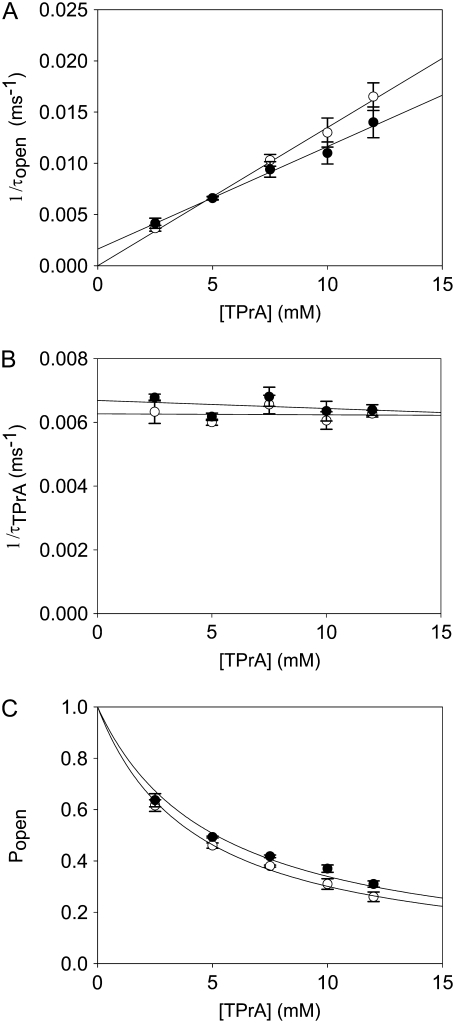
Similar experiments were carried out with internal TPrA and external R13Q. Fig. 4, A–C, shows the kinetics of TPrA in the case of R13Q-free or R13Q-bound channel. The association rate constant for TPrA binding to a R13Q-free channel (kon = 1.35 ± 0.05 × 103 s−1M−1) decreases to kon = 1.00 ± 0.06 × 103 s−1M−1 for TPrA binding to a R13Q-bound channel. The difference between the two kon for TPrA is statistically significant (p = 0.0001). The dissociation rate constant of R13Q-free channel (koff = 6.22 ± 0.25 s−1) is consistent with that of R13Q-bound channel (koff = 6.49 ± 0.48 s−1). There is no significant difference between these two estimates of koff. The equilibrium dissociation constants for TPrA calculated from Popen are: 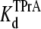Inline graphic = 4.31 ± 0.11 × 10−3 M (R13Q-free), and 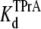Inline graphic = 5.14 ± 0.26 × 10−3 M (R13Q-bound). Thus, the apparent affinity of TPrA decreases when R13Q binds to the channel from external side, based on a decrease in the association rate for TPrA.

FIGURE 4.

FIGURE 4

Open in a new tab

Kinetic analysis for TPrA in the presence of R13Q, carried out as in the previous figure. (A) The reciprocal of open time of TPrA (τopen) as a function of TPrA concentration. (B) The reciprocal of closed time of TPrA (τTPrA) as a function of TPrA concentration. (C) Measured probability that the channel is not occupied by TPrA (Popen) as a function of [TPrA]. Data points and error bars in A–C are the mean ± SD for three to four different single Na channels at each concentration of TPrA. (○) Data when channel was not bound by R13Q from extracellular side; (•) data when channel was bound by R13Q from extracellular side. The solid lines in A are fits to Eq. 2, which were used to measure the association rate constants, kon. The solid lines in B linear fits to the means of determinations of the dissociation rate constants, koff (Eq. 3) from five channels. The solid lines in C are fits to Eq. 4, used to measure the equilibrium dissociation constants 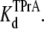Inline graphic Asterisks (*) denote a significant difference (t-test, p < 0.05).

R13X conotoxins decrease the affinity for DEA

DEA is a molecule that provides a fast, complete block of the sodium channel from the intracellular side. Although the individual blocking events are not resolvable, the fast DEA-block can be detected by the decrease of the apparent conductance of the channel after addition of the blocker into the bath solution.

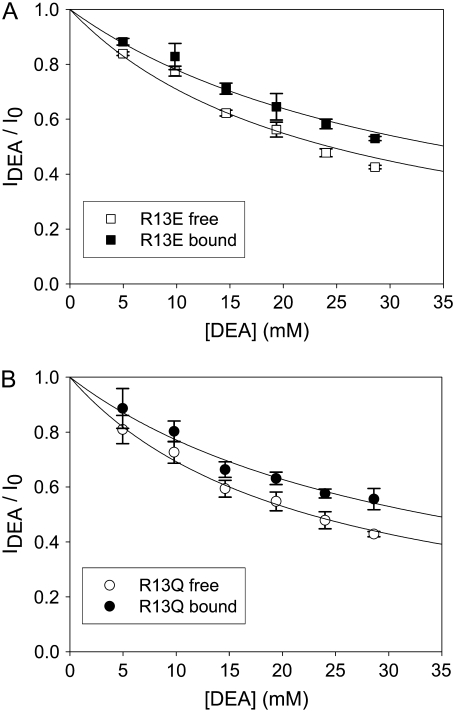
Fig. 5 shows the typical results from an experiment in which a single Na channel recorded in the presence of 33 μM R13E, and then consecutively exposed to 5, 10, and 15 mM internal DEA. Single channel current in the absence of DEA is I0, and the residual single channel current in the presence of DEA is IDEA. IDEA decreases with concentration of DEA (25), distinguishing the mechanism from the discrete reduction in conductance seen on binding of the R13X toxins, for which the amplitude is independent of toxin concentration. Because DEA-block is so fast, the discrete open and closed levels cannot be distinguished, but the channel's probability of not being blocked by DEA can be calculated as Punbound = IDEA/I0. The equilibrium dissociation constant for DEA, 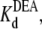Inline graphic can be estimated from Punbound. Fits of the data in Fig. 6 A to Eq. 5 yield 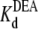Inline graphic = 24.3 ± 1.5 × 10−3 M (R13E-free), and 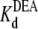Inline graphic = 35.4 ± 1.7 × 10−3 M (R13E-bound); fits of the data in Fig. 6 B to Eq. 5 yield 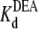Inline graphic = 22.5 ± 0.7 × 10−3 M (R13Q-free), and 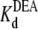Inline graphic = 33.7 ± 1.5 × 10−3 M (R13Q-bound). There is a significant difference between 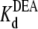Inline graphic (R13X-free) and 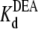Inline graphic (R13X-bound), for X = E or Q, by the usual criterion p ≤ 0.05. Thus, we can say that the affinity for DEA binding to the R13X-blocked channel is weaker than that for the unblocked channel.

FIGURE 6.

FIGURE 6

Open in a new tab

Analysis of DEA block with or without R13X bound to the channel. (A) IDEA/I0 as a function of [DEA ] with or without R13E bound. (B) IDEA/I0 as a function of [DEA] with or without R13Q bound. Data points and error bars in A and B are the mean ± SD for two to three different single Na channels at each concentration of DEA. (□) Data when channel was not bound by R13E from extracellular side; (▪) data when channel was bound by R13E from extracellular side; (○) data when channel was not bound by R13Q from extracellular side; (•) data when channel was bound by R13Q from extracellular side. The solid lines in A and B are fits to Eq. 5, used to measure the equilibrium dissociation constants 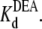Inline graphic Asterisks (*) denote a significant difference (t-test, p < 0.05).

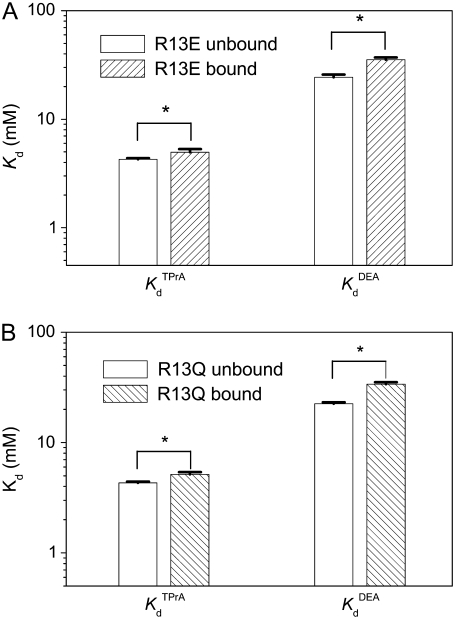
The effects of each of the R13X toxins on binding of each amine blockers are summarized in Fig. 7. For each of the four interacting pairs, there is a significant decrease in amine binding affinity, reflected by the increase in Kd associated with the binding of an individual toxin molecule to the channel. An unexpected observation is that this effect is larger for DEA (a 44%–51% increase in Kd) than for TPrA (a 10%–14% increase), for both toxins. We will return briefly to this issue in the Discussion.

FIGURE 7.

FIGURE 7

Open in a new tab

Inhibition of amine block by R13X binding—summary of estimated dissociation constants. (A) Kd for amines when R13E unbound or bound the channel. (B) Kd for amines when R13Q unbound or bound the channel. Asterisks (*) denote a significant difference (t-test, p < 0.05).

Amine blockers decrease the affinity of conotoxins

The kinetics of R13X block were analyzed by compiling dwell time histograms of easily recognizable, long-lived, partial blocking events (τR13X) and the waiting times between adjacent blocked states (τunblocked). The probability histograms for these two types of events are well described by single-exponential functions. For example, Fig. 8 shows dwell-time histograms, in the square root–log format (35), of R13Q-unblocked events, compiled from single Na channels: A), in the absence of amine; B), in presence of 10 mM TPrA; and C), presence of 10 mM DEA; R13Q-blocked dwell times are plotted: D), in the absence of amine; E), in the presence of 10 mM TPrA; and F), in the presence of 10 mM DEA. The time constants (τR13X and τunblocked) for each case, and the apparent equilibrium dissociation constants derived from them, are shown in Fig. 9. The apparent equilibrium dissociation constants for R13X derivatives (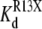Inline graphic(app)) were calculated from Eq. 6, as follows:

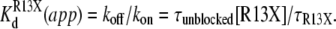graphic file with name M38.gif (6)

FIGURE 9.

FIGURE 9

Open in a new tab

Inhibition of R13X block by the amines, DEA and TPrA—summary of kinetic changes. (A) τunblocked, τR13E, and 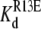Inline graphic(app) (calculated from Eq. 6) for R13E. (B) τunblocked, τR13Q, and 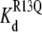Inline graphic(app) (calculated from Eq. 6) for R13Q. Fill patterns (insets) denote data taken in the absence of amine; in the presence of 10 mM TPrA; or in the presence of 10 mM DEA. Pairwise testing (t-test, p < 0.05), and ANOVA, both indicated that there was a significant dependence on amine of Kd and τunblocked, but not τR13Q, for the R13Q experiments. The relatively small apparent differences among the three groups for the R13E experiments did not reach statistical significance by the ANOVA test, consistent with the smaller net charge of R13E.

The results shown in Fig. 9 indicate that both TPrA and DEA cause the 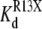Inline graphic(app) to increase, and show that the increase caused by the smaller DEA ion is bigger than that produced by TPrA. At least for R13Q, for which effects are bigger, the effect of toxin on binding results exclusively from a modulation of the association rate constant, with no significant effect on the dissociation rate, reflected by the lack of dependence of blocked times on the presence of the amines. The only significant change for R13E kinetics was seen for the Kd in the presence of DEA. The fact that changes, in both affinity and binding kinetics, for R13E were generally smaller than for R13Q is qualitatively as expected for an electrostatic interaction with the peptide having a lesser charge.

DISCUSSION

Transchannel interactions between μ-conotoxins and amine blockers

In this study, we used planar bilayer recording and single-channel kinetic analysis to investigate the trans-channel interactions in sodium channels between μ-conotoxins and amine blockers. μ-Conotoxins and amines are impermeant cations applied on opposite sides of the membrane. Amines have been used to study the functional architecture of both KV and NaV channels (17,25,39,40). The internal rapid blockage arises from binding of amines to a site deep in the pore (41), which is composed of residues in the S5-S6 loops positioned internal to the DEKA selectivity ring (42–48). Residue 13 of μ-conotoxin GIIIA interacts strongly with domain II. The pore-lining residues close to the selectivity filter, E758, D762, and E765 are part of the high-affinity binding site for μ-conotoxins (33,49,50). Some extra-pore residues of the S5-S6 loop of domain II, A728, S729, D730, and N732 contribute to the μ-conotoxin binding site as well (51,52). Thus, the major identified interactions of the μ-conotoxins are with residues lying outside the selectivity filter, and these are reinforced by some presumably long-range interactions with residues in the DEKA ring.

μ-Conotoxin-amine interactions

μ-Conotoxin GIIIA, in its native form, blocks the skeletal muscle sodium channel in an all-or-none manner. Replacement of one critical residue (R13) yields peptides that only partially block single-channel current. R13E, in which arginine is replaced with glutamate, has a nominal net charge of +4; for R13Q, net charge is +5, are two such partially blocking derivatives. Previous studies have shown that a number of monovalent amines act from the cytoplasmic end of single, skeletal muscle sodium channel as all-or-none blockers. The mutual trans-channel interactions between these two classes of blocker were studied in detail using the kinetic analysis presented in the Results.

Fig. 10 depicts a classic model of a cyclic equilibrium in which two ligands bind to nonoverlapping sites on a protein. The pseudo first order equilibrium constants (A1, A2, T1, T2) describe the relative occupancy of adjacent states in the scheme, and are constrained by the assumptions of steady state and microscopic reversibility expressed in the following identity:

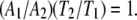graphic file with name M42.gif (7)

FIGURE 10.

FIGURE 10

Open in a new tab

A hypothetical four-state model for a simple binding interaction between amines and toxin derivatives. U is the unoccupied state, Bamine is the amine-bound state, Btoxin is the toxin-bound state, Bamine/toxin is the doubly occupied, blocked state. The symbol, Δ, represents the amine (TPrA or DEA) bound from internal side; (*) represents the toxin (R13E or R13Q) bound from external side. A1 is the equilibrium dissociation constant for amine binding to the unoccupied channel; A2 is the equilibrium dissociation constant for amine binding to the toxin-occupied channel; T1 is the equilibrium dissociation constant for toxin binding to the unoccupied channel; T2 is the equilibrium dissociation constant for toxin binding to the amine-occupied channel.

The pseudo first-order equilibrium constants are defined by four relationships of the following form:

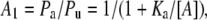graphic file with name M43.gif (8)

where Pa and Pu are the probabilities that the channel is unbound, or bound only by amine, respectively; Ka is the 2nd order equilibrium dissociation constant for amine binding, and [A] is the amine concentration. Thus, Eq. 7, three equations of the form of Eq. 8, and the conservation Eq. 9 can be solved to determine A1, A2, T1, and T2, and the probabilities of occupancy of the four states, in terms of the experimentally defined 2nd order dissociation constants.

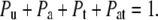graphic file with name M44.gif (9)

Here, similar to the definitions above, Pt is the probability that the channel is bound only by toxin, and Pat is the probability that it is bound simultaneously by amine and toxin.

For each amine-toxin pair, three of the second order dissociation constants can be determined directly from the data: Ka, Kt, and Ka(T). Ka(T), the dissociation constant for amine binding to a toxin-bound channel, is determined from amine blocking kinetics in identified toxin partial block events. The reverse is not possible, however, given that amine blocked times are much shorter than bound dwell times for the toxin, and experiments must be done with a probability of amine block of ∼0.5 to be able to resolve the toxin binding events. Thus, a more rigorous estimate of Ka(T) comes from the assumption of microscopic reversibility and steady state, after experimental determination of the other parameters. The results of these calculations are given in Tables 1 and 2.

TABLE 1.

Reciprocal changes in apparent dissociation constants: Kd (antagonist bound)/Kd (control)

TPrA (toxin antagonist) Toxin (TPrA antagonist) DEA (toxin antagonist) Toxin (DEA antagonist)
R13E 1.10 1.04 1.51 1.48
R13Q 1.14 1.07 1.44 1.51
Open in a new tab

Values were calculated assuming microscopic reversibility and steady state among the four possible occupancy states (Fig. 10).

TABLE 2.

Calculated occupancy of different binding states

Punbound Pamine Ptoxin Pamine/toxin
TPrA-R13E 0.474 0.326 0.120 0.080
TPrA-R13Q 0.425 0.293 0.170 0.112
DEA-R13E 0.622 0.186 0.157 0.035
DEA-R13Q 0.558 0.167 0.223 0.051
Open in a new tab

Values were calculated assuming microscopic reversibility and steady state among the four possible occupancy states (Fig. 10).

Table 1 summarizes the reciprocal changes in Kd for both R13X and amines (see also Fig. 7). Each of the two monovalent amines shows inhibitory interactions with the toxins, but they differ in magnitude. Estimated Kd changes were 4%–14% for TPrA interactions, but larger effects of 44%–51% were estimated for DEA. For each toxin-amine pair, the reciprocal effects of toxin on amine binding, and vice versa, differ by no more than 7%, and are likely not significant, given the experimental challenge to determine small differences in these derived parameters. In energetic terms, the reciprocal changes are modest. Changes in binding energy, in units of RT, (ΔΔG/RT) = ln [Kd(antagonist bound)/Kd (control)], range from 0.05 to 0.12 for TPrA, whereas for DEA they range from 0.36 to 0.45. Nonetheless, they reflect a consistent, mutual, inhibitory modulation of binding, the largest estimated effect being for DEA-R13Q, and the smallest for the TPrA interactions.

Although, in three of four cases (Table 1, columns), R13E seems to show slightly weaker transchannel interactions than R13Q, it is hard to argue that this represents a significant difference. This may reflect a difficulty of resolution. The nominal net charge changes from +5 to +4 between these two derivatives, but a functional estimate of the pK of the 13E residue suggests that it may be charged only ∼50% of the time when R13E is bound in the channel's vestibule (23). This would mean the net charges of the bound R13Q and R13E would different only by 0.5e—about a 10% difference. Nonetheless, there is much data consistent with the idea that residue 13 enters most deeply into the pore (22,53), and thus, it is the residue likely to most closely approach the amine binding site. The result, that R13Q does inhibit amine binding, rules out the possibility that the interaction is strongly dominated by the charge on residue-13 side chain. Rather, the inhibitory interaction must result from significant contributions of all, or several, of the toxin charges.

A paradox: differing trans-channel interactions of two monovalent amines that compete for a common binding site

Even though TPrA and DEA both have a single positive charge, and functionally compete for a common site in the inner cavity (Fig. 1), TPrA is less effective than DEA at inhibiting toxin binding (Fig. 9). Nonetheless, this result is consistent with the results of potential shifts of amine block caused by toxins, presented in the companion article (34), and will be discussed further there.

Two factors might provide a qualitative basis for this observation. First, the two amines could bind at slightly different positions in the lumen of the pore. However, there is no indication from electrical distance measurements that DEA binds deeper in the pore. Our earlier survey using Na channels from bovine cardiac muscle yielded zδ values of 0.47 and 0.64 for DEA and TPrA respectively (17), whereas the more detailed analysis in the companion article ((34); Table 1) showed no significant difference over four groups of experiments for each amine, with and without conotoxins. Values for zδ ± SE were 0.53 ± 0.02 and 0.54 ± 0.04, for DEA and TPrA, respectively (n = 4 groups of experiments for each amine). Hence, voltage dependence of block gives no evidence of deeper penetration into the pore by DEA. Nonetheless, it is conceivable that the potential gradient is shallow in the inner cavity of the channel, and that the physical positions of two amines could be sufficiently different to change direct interactions with toxin, or coupling through permeant ions. A second contributing factor might result from the different sizes of amines. For DEA, the radii from the central N atom along the substituent “chains” ranges from ∼1 Å for H to ∼2.4 Å for an ethyl group, whereas for the propyl chains of TPrA the value is ∼6.4 Å. This geometric consideration suggests that DEA might enter into a more intimate interaction with the bound toxin, or with Na+, leading to a stronger interaction than for the bulkier TPrA ion.

CONCLUSION

Clear results from this study are: 1), block by DEA and TPrA is mutually exclusive, suggesting that they bind to a common site in the channel's inner cavity; 2), binding of partially blocking, R13X μ-conotoxin derivatives to the extracellular vestibule, and the amines, DEA or TPrA, to the inner cavity, is mutually inhibitory, but not mutually exclusive; and 3), the strength of the transchannel conotoxin-amine inhibitory interaction is not determined solely by the charges of these agents.

Two features of our data prompt further critical examination of the hypothesis of an electrostatic interaction between bound toxin and amine blockers. These are: first, the stronger interaction of DEA than TPrA, and second, the paucity of evidence for dependence of the interaction on toxin charge. The simplest electrostatic picture, in which the amines are considered as point charges binding to exactly the same site in the channel, near the charge of the toxin, may be quantitatively inaccurate, because of contributions from any of the following: 1), differences in their sizes and shapes of the amines; 2), allosteric changes induced in the channel protein by amine binding; or 3), occupancy issues, including possible coupling to permeant ion movement, as has been suggested for potassium channels (54). These possibilities are considered more extensively in the light of additional experiments, in the companion article (34).

Acknowledgments

G.W.Z. is an Alberta Heritage Foundation for Medical Research Senior Scholar and holds a Canada Research Chair. We thank Dr. Iván Sierralta for providing preliminary data. We are grateful to Dr. John Daly, National Institute for Digestive Diseases and Kidney, for providing batrachotoxin, to Christopher Bladen for making membrane preparations, and to Dr. Denis McMaster, Peptides Services, Faculty of Medicine, University of Calgary, for meticulous peptide synthesis and purification. We are grateful to Drs. Dean McIntyre and Hans Vogel of the University of Calgary Bio-NMR Centre for NMR tests on the peptides. Maintenance and operation of the Bio-NMR Centre is supported by the Canadian Institutes of Health Research and the University of Calgary. Thanks to Dr. Sergei Noskov for reading a draft of the manuscript.

This work was supported by the Canadian Institutes of Health Research (CIHR), the Heart and Stroke Foundation of Alberta, NWT and Nunavut, and the National Institutes of Health, USA. R.J.F. received salary support as an Medical Research Council of Canada/CIHR Distinguished Scientist and an AHFMR Medical Scientist.

Abbreviations used: BTX, batrachotoxin; DEA, diethylammonium; HPLC, high-performance liquid chromatography; TPrA, tetrapropylammonium; R13X, derivatives of μ-conotoxin GIIIA (X = E or Q).

Editor: Dorothy A. Hanck.

References

  • 1.Hess, P., and R. W. Tsien. 1984. Mechanism of ion permeation through calcium channels. Nature. 309:453–456. [DOI] [PubMed] [Google Scholar]
  • 2.Almers, W., and E. W. McCleskey. 1984. Non-selective conductance in calcium channels of frog muscle: calcium selectivity in a single file pore. J. Physiol. 353:585–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Bernèche, S., and B. Roux. 2001. Energetics of ion conduction through the K+ channel. Nature. 414:73–77. [DOI] [PubMed] [Google Scholar]
  • 4.Berneche, S., and B. Roux. 2003. A microscopic view of ion conduction through the K+ channel. Proc. Natl. Acad. Sci. USA. 100:8644–8648. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Morais-Cabral, J. H., Y. Zhou, and R. MacKinnon. 2001. Energetic optimization of ion conduction rate by the K+ selectivity filter. Nature. 414:37–42. [DOI] [PubMed] [Google Scholar]
  • 6.Hodgkin, A. L., and R. D. Keynes. 1955. The potassium permeability of a giant nerve fibre. J. Physiol. 128:61–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Begenisich, T. B., and P. DeWeer. 1980. Potassium flux ration in voltage-clamped squid giant axons. J. Gen. Physiol. 76:83–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Stampe, P., and T. Begenisich. 1996. Unidirectional K+ fluxes through recombinant Shaker potassium channels expressed in single Xenopus oocytes. J. Gen. Physiol. 107:449–457. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Armstrong, C. M. 1975. Ionic pores, gates and gating currents. Q. Rev. Biophys. 7:179–210. [DOI] [PubMed] [Google Scholar]
  • 10.Yellen, G. 1984. Relief of Na+ block of Ca2+-activated K+ channels by external cations. J. Gen. Physiol. 84:187–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Begenisich, T. B., and D. Busath. 1981. Sodium flux ratio in voltage-clamped squid giant axons. J. Gen. Physiol. 77:489–502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Busath, D., and T. B. Begenisich. 1982. Unidirectional sodium and potassium fluxes through the sodium channel of squid giant axons. Biophys. J. 40:41–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Ravindran, A., H. Kwiecinski, O. Alvarez, G. Eisenman, and E. Moczydlowski. 1992. Modeling ion permeation through batrachotoxin-modified Na+ channels from rat skeletal muscle with a multi-ion pore. Biophys. J. 61:494–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.French, R. J., J. F. Worley III, W. F. Wonderlin, A. S. Kularatna, and B. K. Krueger. 1994. Ion permeation, divalent ion block and chemical modifications of single sodium channels: description by single-occupancy, rate theory models. J. Gen. Physiol. 103:447–470. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Neyton, J., and C. Miller. 1988. Potassium blocks barium permeation through a calcium-activated potassium channel. J. Gen. Physiol. 92:549–567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Woodhull, A. M. 1973. Ionic blockage of sodium channels in nerve. J. Gen. Physiol. 61:687–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Zamponi, G. W., and R. J. French. 1994. Amine blockers of the cytoplasmic mouth of sodium channels: a small structural change can abolish voltage dependence. Biophys. J. 67:1015–1027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Seyama, I., C. H. Wu, and T. Narahashi. 1980. Current-dependent block of nerve membrane sodium channels by paragracine. Biophys. J. 29:531–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Cruz, L. J., W. R. Gray, B. M. Olivera, R. D. Zeikus, L. Kerr, D. Yoshikami, and E. Moczydlowski. 1985. Conus geographus toxins that discriminate between neuronal and muscle sodium channels. J. Biol. Chem. 260:9280–9288. [PubMed] [Google Scholar]
  • 20.Becker, S., E. Prusak-Sochaczewski, G. Zamponi, A. G. Beck-Sickinger, R. D. Gordon, and R. J. French. 1992. Action of derivatives of μ-conotoxin GIIIA on sodium channels. Single amino acid substitutions in the toxin separately affect association and dissociation rates. Biochemistry. 31:8229–8238. [DOI] [PubMed] [Google Scholar]
  • 21.French, R. J., E. Prusak-Sochaczewski, G. W. Zamponi, S. Becker, A. S. Kularatna, and R. Horn. 1996. Interactions between a pore-blocking peptide and the voltage sensor of the sodium channel: an electrostatic approach to channel geometry. Neuron. 16:407–413. [DOI] [PubMed] [Google Scholar]
  • 22.Hui, K., G. Lipkind, H. A. Fozzard, and R. J. French. 2002. Electrostatic and steric contributions to block of the skeletal muscle sodium channel by μ-conotoxin. J. Gen. Physiol. 119:45–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Hui, K., D. McIntyre, and R. J. French. 2003. Conotoxins as sensors of local pH and electrostatic potential in the outer vestibule of the sodium channel. J. Gen. Physiol. 122:63–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.O'Leary, M. E., and R. Horn. 1994. Internal block by human heart sodium channels by symmetrical tetra-alkylammoniums. J. Gen. Physiol. 104:507–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Zamponi, G. W., and R. J. French. 1993. Dissecting lidocaine action: diethylamine and phenol mimic separate modes of lidocaine block of sodium channels from heart and skeletal muscle. Biophys. J. 65:2335–2347. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Zamponi, G. W., and R. J. French. 1994. Arrhythmias during phenol therapies: a specific action on cardiac sodium channels? Circulation. 89:914. [PubMed] [Google Scholar]
  • 27.Krueger, B. K., J. F. Worley III, and R. J. French. 1983. Single sodium channels from rat brain incorporated into planar lipid bilayers. Nature. 303:172–175. [DOI] [PubMed] [Google Scholar]
  • 28.Khodorov, B. I. 1985. Batrachotoxin as a tool to study voltage-sensitive sodium channels of excitable membranes. Prog. Biophys. Mol. Biol. 45:57–148. [DOI] [PubMed] [Google Scholar]
  • 29.Cahalan, M. D., and T. B. Begenisich. 1976. Sodium channel selectivity: dependence on internal permeant ion concentration. J. Gen. Physiol. 68:111–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Begenisich, T. B., and M. D. Cahalan. 1980. Sodium channel permeation in squid axons I: reversal potential experiments. J. Physiol. 307:217–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Garber, S. S. 1988. Symmetry and asymmetry of permeation through alkaloid-modified Na+ channels. Biophys. J. 54:767–776. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Zamponi, G. W., D. D. Doyle, and R. J. French. 1993. State-dependent block underlies the tissue specificity of lidocaine action on batrachotoxin-activated cardiac sodium channels. Biophys. J. 65:91–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Chang, N. S., R. J. French, G. M. Lipkind, H. A. Fozzard, and S. Dudley, Jr. 1998. Predominant interactions between μ-conotoxin Arg-13 and the skeletal muscle Na+ channel localized by mutant cycle analysis. Biochemistry. 37:4407–4419. [DOI] [PubMed] [Google Scholar]
  • 34.Pavlov, E., T. Britvina, J. R. McArthur, Q. Ma, I. C. Sierralta, G. W. Zamponi, and R. J. French. 2008. Trans-channel interactions in batrachotoxin-modified skeletal muscle sodium channels. Voltage dependent block by cytoplasmic amines, and the influence of μ-conotoxin GIIIA derivatives and permeant ions. Biophys. J. 95:4277–4288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Sigworth, F. J., and S. M. Sine. 1987. Data transformations for improved display and fitting of single-channel dwell time histograms. Biophys. J. 52:1047–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Wonderlin, W. F., R. J. French, and N. J. Arispe. 1990. Recording and analysis of currents from single ion channels. In Neuromethods, Vol. 14. Neurophysiological Techniques: Basic Methods and Concepts. A. A. Boulton, G. B. Baker, and C. H. Vanderwolf, editors. Humana Press, Clifton, NJ. 35–142.
  • 37.Colquhoun, D., and F. J. Sigworth. 1983. Fitting and statistical analysis of single-channel records. In Single-Channel Recording. B. Sakmann and E. Neher, editors. Plenum Press, New York, NY. 191–263.
  • 38.Favre, I., and E. Moczydlowski. 1999. Simultaneous binding of basic peptides at intracellular sites on a large conductance Ca2+-activated K+ channel. Equilibrium and kinetic basis of negatively coupled ligand interactions. J. Gen. Physiol. 113:295–320. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Armstrong, C. M., and B. Hille. 1998. Voltage-gated ion channels and electrical excitability. Neuron. 20:371–380. [DOI] [PubMed] [Google Scholar]
  • 40.French, R. J., and J. J. Shoukimas. 1985. An ion's view of the potassium channel. The structure of the permeation pathway as sensed by a variety of blocking ions. J. Gen. Physiol. 85:669–698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 41.Kimbrough, J. T. and K. J. Gingrich. 2000. Quaternary ammonium block of mutant Na+ channels lacking inactivation: features of a transition-intermediate mechanism. J. Physiol. 529:93–106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Sunami, A., S. C. Dudley, Jr., and H. A. Fozzard. 1997. Sodium channel selectivity filter regulates antiarrhythmic drug binding. Proc. Natl. Acad. Sci. USA. 94:14126–14131. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Ragsdale, D. S., J. C. McPhee, T. Scheuer, and W. A. Catterall. 1994. Molecular determinants of state-dependent block of Na+ channels by local anesthetics. Science. 265:1724–1728. [DOI] [PubMed] [Google Scholar]
  • 44.Fozzard, H. A., P. J. Lee, and G. M. Lipkind. 2005. Mechanism of local anesthetic drug action on voltage-gated sodium channels. Curr. Pharm. Des. 11:2671–2686. [DOI] [PubMed] [Google Scholar]
  • 45.Lipkind, G. M., and H. A. Fozzard. 2005. Molecular modeling of local anesthetic drug binding by voltage-gated sodium channels. Mol. Pharmacol. 68:1611–1622. [DOI] [PubMed] [Google Scholar]
  • 46.Tikhonov, D. B., I. Bruhova, and B. S. Zhorov. 2006. Atomic determinants of state-dependent block of sodium channels by charged local anesthetics and benzocaine. FEBS Lett. 580:6027–6032. [DOI] [PubMed] [Google Scholar]
  • 47.McNulty, M. M., G. B. Edgerton, R. D. Shah, D. A. Hanck, H. A. Fozzard, and G. M. Lipkind. 2007. Charge at the lidocaine binding site residue Phe-1759 affects permeation in human cardiac voltage-gated sodium channels. J. Physiol. 581:741–755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 48.Wang, S. Y., D. B. Tikhonov, B. S. Zhorov, J. Mitchell, and G. K. Wang. 2007. Serine-401 as a batrachotoxin- and local anesthetic-sensing residue in the human cardiac Na+ channel. Pflugers Arch. 454:277–287. [DOI] [PubMed] [Google Scholar]
  • 49.Dudley, S. C., H. Todt, G. Lipkind, and H. A. Fozzard. 1995. A μ-conotoxin-insensitive Na+ channel mutant: possible localization of a binding site at the outer vestibule. Biophys. J. 69:1657–1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Li, R. A., I. L. Ennis, P. Vélez, G. F. Tomaselli, and E. Marbán. 2000. Novel structural determinants of μ-conotoxin (GIIIB) block in rat skeletal muscle (μ1) Na+ channels. J. Biol. Chem. 275:27551–27558. [DOI] [PubMed] [Google Scholar]
  • 51.Chahine, M., J. Sirois, P. Marcotte, L.-Q. Chen, and R. G. Kallen. 1998. Extrapore residues of the S5–S6 loop of domain 2 of the voltage-gated skeletal muscle sodium channel (rSkM1) contribute to the μ-conotoxin GIIIA binding site. Biophys. J. 75:236–246. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Cummins, T. R., F. Aglieco, and S. D. Dib-Hajj. 2002. Critical molecular determinants of voltage-gated sodium channel sensitivity to mu-conotoxins GIIIA/B. Mol. Pharmacol. 61:1192–1201. [DOI] [PubMed] [Google Scholar]
  • 53.Choudhary, G., M. P. Aliste, D. P. Tieleman, R. J. French, and S. C. Dudley, Jr. 2007. Docking orientation of μ-conotoxin GIIIA in the sodium channel outer vestibule. Channels (Austin). 1:344–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Thompson, J., and T. Begenisich. 2000. Interaction between quaternary ammonium ions in the pore of potassium channels. Evidence against an electrostatic repulsion mechanism. J. Gen. Physiol. 115:769–782. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES