Skip to main content
. 2008 Jul 18;95(9):4205–4216. doi: 10.1529/biophysj.108.136499

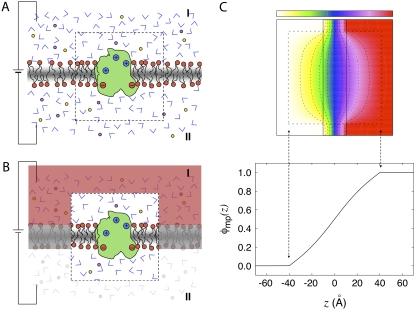
FIGURE 1.

FIGURE 1

Schematic representation of the reduction to a finite system and Poisson-Boltzmann calculation. (A) A thermodynamic membrane system with a transmembrane potential is separated into a microscopic subsystem (inner region) and its surrounding baths (outer region). The inner region (delineated by the dashed box) comprises the protein as well as the membrane and bulk solution in its neighborhood, while the outer region includes the aqueous salt solutions, the electrodes, and the EMF. The membrane is centered at z = 0 and extends in the xy plane. The electrode on side II is grounded (V = 0). (B) Representation of the same system with the degrees of freedom of the outer region integrated out and their influence on the inner region approximated using a continuum electrostatic Poisson-Boltzmann theory based on Eq. 4. (C) The effect of the transmembrane potential from an infinite thermodynamic system onto the finite subsystem is illustrated using a continuum electrostatic calculation based on the modified Poisson-Boltzmann theory (3). At the top is shown the dimensionless function φmp acting on a cubic central inner region of 80 Å on the side (indicated by the dashed line box). The dimensionless function φmp varies from 0.0 of the left (white) to 1.0 on the right (red); the contour levels indicated by colors and dashed lines are set to 0.0 (white), 0.20 (yellow), 0.35 (green), 0.50 (blue), 0.65 (purple), 0.80 (violet), and 1.0 (red). The variation of φ along the z axis cutting through the center of the box is shown at the bottom. The function φ was calculated by solving Eq. 4 numerically. In the inner region, the dielectric constant is set to 1 and the ionic screening constant is set to zero. For the aqueous phase of the outer region, a dielectric constant of 80 and an ionic concentration of 150 mM were assumed. The thickness of the membrane slab in the outer region is 20 Å and its dielectric constant is set to 2. The continuum electrostatic calculations were carried out using the PBEQ module of CHARMM using a cubic grid of 201 points spaced by 1 Å. The equation was solved by using the overrelaxation method and ∼500 iterations were required to reach convergence.