efficient association study design via power-optimized tag SNP selection

Abstract

Discovering statistical correlation between causal genetic variation and clinical traits through association studies is an important method for identifying the genetic basis of human diseases. Since fully resequencing a cohort is prohibitively costly, genetic association studies take advantage of local correlation structure (or linkage disequilibrium) between single nucleotide polymorphisms (SNPs) by selecting a subset of SNPs to be genotyped (tag SNPs). While many current association studies are performed using commercially available high-throughput genotyping products that define a set of tag SNPs, choosing tag SNPs remains an important problem for both custom follow-up studies as well as designing the high-throughput genotyping products themselves. The most widely used tag SNP selection method optimizes over the correlation between SNPs (r²). However, tag SNPs chosen based on an r² criterion do not necessarily maximize the statistical power of an association study. We propose a study design framework that chooses SNPs to maximize power and efficiently measures the power through empirical simulation. Empirical results based on the HapMap data show that our method gains considerable power over a widely used r²-based method, or equivalently reduces the number of tag SNPs required to attain the desired power of a study. Our power-optimized 100k whole genome tag set provides equivalent power to the Affymetrix 500k chip for the CEU population. For the design of custom follow-up studies, our method provides up to twice the power increase using the same number of tag SNPs as r²-based methods. Our method is publicly available via web server at http://design.cs.ucla.edu.

Introduction

Discovering statistical correlation between causal genetic variation and clinical traits through association studies is an important method for identifying the genetic basis of human disease. (Balding, 2006; Carlson et al., 2004a). Typically, a genetic association study gathers case/control individuals, collects genetic variation information such as genotypes at single nucleotide polymorphisms (SNPs), and tests the significance of association for each SNP using a statistical test such as a χ² test. Since fully resequencing a cohort is prohibitively costly, a set of representative SNPs (called tags or tag SNPs) are chosen as proxies for nearby SNPs, utilizing the local correlation structure of SNPs (or linkage disequilibrium) to find associations (Pritchard & Przeworski, 2001). While many current association studies are performed using commercially available high-throughput genotyping products that define a set of tag SNPs, selection of these SNPs remains an important problem for both custom follow-up studies as well as designing the high-throughput genotyping products themselves (Stram, 2004, 2005; de Bakker et al., 2005; Cousin et al., 2003, 2006; Halperin et al., 2005; Lin & Altman, 2004; Pardi et al., 2005; Qin et al., 2006; Saccone et al., 2006; Carlson et al., 2004b).

In the context of association studies, maximizing statistical power is the most relevant goal of tag SNP selection. Since the actual causal SNP is not known, the statistical power of an association study is defined as the average power over all possible causal SNPs. Recent availability of reference data sets such as the HapMap (Hinds et al., 2005; HapMap, 2003, 2005) allows us to empirically measure power of an association study design (de Bakker et al., 2005; Pe’er et al., 2006; Kruglyak, 2005). A standard method for picking tags is greedily choosing the smallest number of SNPs with a minimum cut-off of correlation (r²) between tag SNPs and uncollected SNPs (de Bakker et al., 2005; Carlson et al., 2004b; HapMap, 2003, 2005). However, choosing tag SNPs based on r² alone does not necessarily maximize power, because r² does not take into account minor allele frequency (MAF) which also inuences power.

In this paper, we present a exible study design framework that chooses tag SNPs to maximize the statistical power of an association study.

The underlying intuition is that we quickly find the “key tag SNPs” that contribute a considerable amount of power. The power a tag SNP contributes depends on (1) the coverage of a tag SNP (the number of putative causal SNPs a tag SNP can cover), (2) the correlation (the r² between a tag SNP and each causal SNP it covers), and (3) the MAF of each causal SNP. We observe that r²-based methods do not consider (3) and maximize (1) by setting (2) to a fixed threshold. Instead, we use a greedy procedure that evaluates each candidate tag SNP’s possible average power increase, and selects the best SNP as a tag SNP at each step. By evaluating the average power increase, we take into account all three aspects of a tag SNP. By not fixing a minimum value of r², we allow more exibility in selecting a tag SNP of maximum power. For example, if a tag SNP has a low r² to causal SNPs but covers many common SNPs (bad at (2) but good at (1) and (3)), we can select the SNP based on the power increase unlike the r²-based methods.

Empirical simulations based on the HapMap ENCODE regions show that our power-optimized method requires 21% fewer tag SNPs on average than widely used r²-based methods, to achieve equivalent power. When applied to whole genome association mapping, our power-optimized tag sets consistently outperform the r²-based tag sets across all populations. We compare our designs to the commercial products as well. Our 100k tag set provides equivalent power to the Affymetrix 500k chip for European and Asian populations. In addition, our 300k tag set outperforms the Illumina 550k chip across all three HapMap populations. We apply our method to the custom follow-up study design problem where the goal is to select tag SNPs in addition to those already present on a commercial product to maximize the statistical power within a region of interest. Our method provides up to twice the power increase using the same number of additional tag SNPs compared to the widely used r²-based methods.

Since study parameters such as relative risk are generally unknown, a possible pitfall of using statistical power instead of a study-independent measure such as r² is “fitting” the design to an incorrect parameter. We show that when the parameters are correct our method performs optimally, and when the parameters are incorrect our method still out-performs or performs similarly to the widely used r²-based methods, within a wide range of parameters.

During the course of design, our procedure requires us to evaluate the power of candidate tag sets numerous times, thus the use of empirical simulation for measuring power (de Bakker et al., 2005) is computationally impractical. We combine the use of an analytical approximation for the power in our tag selection method with an efficient empirical simulation that can accurately measure the power of a tag set. The efficiency of our method allows us to design an association study in one ENCODE region in 3 seconds and a genome wide study in 1.5 CPU hours. The empirical simulation for accurately measuring power is based on a standard technique described in de Bakker et al. (2005). To the best of our knowledge, no one has analyzed this standard simulation procedure with respect to its accuracy. We improve the efficiency of this simulation and scale it to the whole genome using a sampling procedure, for which we derive the corresponding confidence intervals. This allows us to determine the number of sampling iterations required for a given level of accuracy. The key insight in this sampling procedure is that the variance of the estimate of the power is independent of the shape of the distribution of the true power over the causal SNPs.

Previous works in tag SNP selection include haplotype-based methods (Johnson et al., 2001; Stram, 2004, 2005; Lin & Altman, 2004; Halperin et al., 2005), correlation-based methods (Carlson et al., 2004b; Qin et al., 2006; HapMap, 2005; de Bakker et al., 2005), and power-based methods (Byng et al., 2003; Pardi et al., 2005; Cousin et al., 2003, 2006; Saccone et al., 2006). The correlation-based methods are power-based methods in that r² is closely related to power (Pritchard & Przeworski, 2001), but here we group power-based methods separately based on whether MAF is taken into account. Among the power-based methods, Byng et al. (2003); Pardi et al. (2005) use the generalized linear model to test the association between the region of interest and the disease. Their approach is different from ours which considers single SNP association for each SNP in order to detect and locate the association. Cousin et al. (2003, 2006) maximizes average power over all possible parameters, specifically over a relative penetrance from 0 to 1 which corresponds to the relative risk from 1 to ∞. Since such a high relative risk is often of little interest in the current association studies, and since sometimes the relative risk can be approximated from the previous studies, our method can be more suitable for those cases by allowing a exible choice of parameter values or ranges. Saccone et al. (2006) focus on the observation that the power is affected by the phase of the correlation, whether a tag SNP and the causal SNP are correlated positively or negatively. However, if we use r² as a correlation measure instead of D′ they use (Devlin & Risch, 1995), the power is approximately independent of the phase of correlation (Pritchard & Przeworski, 2001). Thus, selecting tag SNPs based on the phase may not maximize power.

The implementation of our method is publicly available via web server at http://design.cs.ucla.edu. On this web site, we provide power analysis for all popular commercial products as well as candidate gene study designs for every gene in the human genome.

Results

Performance

We evaluate the performance of our power-optimized method by comparing it to those of widely used r²-based methods. Pairwise r² tagging (Carlson et al., 2004b; de Bakker et al., 2005; HapMap, 2005) is the most common r²-based method. It greedily selects tags until every SNP is covered with a given minimum r² threshold. Best-N r² is another r²-based method (de Bakker et al., 2005). It greedily selects a fixed number of tags to cover as many SNPs as possible with a given minimum r² threshold. We use the HapMap ENCODE regions which consist of ten 500kb regions that have been widely used to evaluate design methodologies due to their complete ascertainment of common SNPs (MAF ≥5%). In this experiment and throughout this paper, we assume a multiplicative disease model with fixed relative risk of 1.2 and disease prevalence of 0.01. We assume a uniform distribution of causal SNPs over all common SNPs defined by a 5% MAF threshold, and use a 5% region-wide significance level (α) for statistical tests. We note that other studies often assume a varying relative risk depending on MAF. For example, Marchini et al. (2007) and de Bakker et al. (2005) set a relative risk so that a single SNP can have a 95% of nominal power at a nominal significance level of 1% (ignoring multiple hypothesis testing). This corresponds to a relative risk of 1.21 for a SNP of 50% MAF and a relative risk of 1.48 for a SNP of 5% MAF when 4,000 cases and 4,000 controls are used. In this paper, we assume a uniform relative risk of 1.2, to evaluate the worst case power over all disease models with relative risk of 1.2 or above. This model is often more realistic than the varying relative risk model for the case that the relative risk is estimated from previous studies. These assumptions are used in both analytically designing tag sets and empirically measuring their power.

First, we consider the ENr232 ENCODE region containing 533(CEU), 596(CHB), 573(JPT), and 740(YRI) common SNPs. The full set of common SNPs achieves the maximum possible power. We will call this the full-SNP-set power. For each population, assuming 4,000 cases and 4,000 controls (= 8,000/8,000 chromosomes), we use our power-optimized method to construct 100 different tag sets of increasing size. The number of tags in each tag set is increased by 1% of total common SNPs.

For comparison, we construct another 100 tag sets of similar size using pairwise r² tagging. Since we can only vary the r² threshold in pairwise r² tagging, we use binary-search over the r² threshold with a precision of 0.001, to find a tag set having the desired size as closely as possible. Then we construct another 100 tag sets using best-N r². We use a widely used threshold of r² = 0.8 for best-N r². We will use this threshold for every experiment using best-N r².

For each tag set, we use the standard empirical simulation for estimating power (de Bakker et al., 2005). We create 100,000 null panels for multiple hypothesis correction and 100,000 alternate panels for estimating power, which gives a 95% confidence interval for a <0.6% error in power. We will use the same number of panels whenever we measure the power of a tag set through the paper.

Figure 1 shows the results of the CEU population. The results of the other populations are shown in Supplementary Figure 11. The power-optimized method reaches the full-SNP-set power (dashed horizontal line) faster than both r²-based methods. The range of the number of tag SNPs (x-axis) is shown from zero up to the required number of tag SNPs for best-N r² to cover every SNP. Thus, at the end of the graph, pairwise r² tagging and best-N r² become an equivalent procedure, where the threshold of pairwise r² tagging happens to be 0.8, and best-N r² happens to cover every SNP with r² = 0.8. To achieve 95% of full-SNP-set power, our power-optimized method requires 37, 71, 57, and 207 SNPs while pairwise r² tagging requires 85, 124, 120, and 259 SNPs and best-N r² requires 37, 89, 80, and 310 SNPs in the CEU, CHB, JPT, and YRI populations respectively. Pairwise r² tagging shows low power with a small number of tags since the r² has to be very low to cover every SNP. It has been already reported that overly lowering r² threshold of pairwise r² tagging may result in a performance not better than a random tags (de Bakker et al., 2005). Best-N r² shows a good performance with a small number of tags, although not better than our power-optimized method, and often shows a worse performance than pairwise r² tagging with a large number of tags, as shown in Figure 1.

Figure 1.

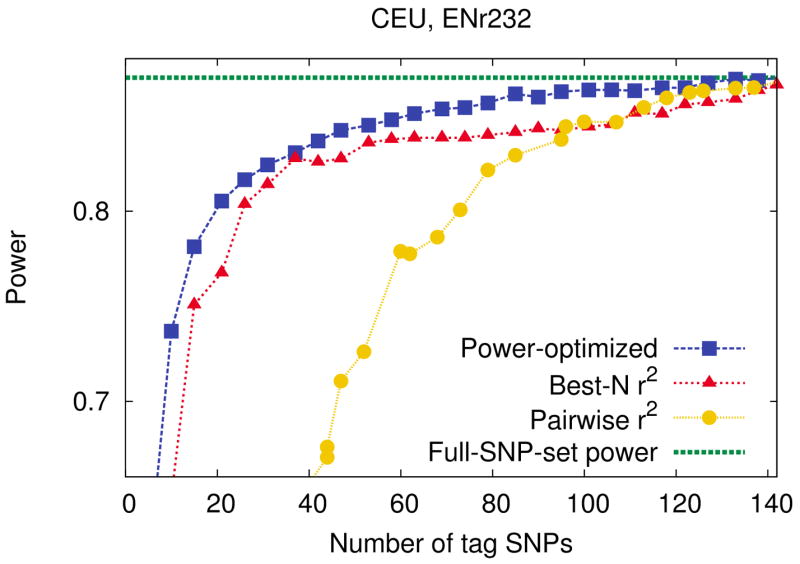
Power comparison between our power-optimized tag SNP selection method and a widely used r²-based methods, pairwise r² tagging and best-N r², in the ENr232 ENCODE region of the CEU population. We use a 5% region-wide significance level, a 5% MAF threshold for causal SNPs, and assume relative risk of 1.2, disease prevalence of 0.01, and 4,000 cases and 4,000 controls. We use the r² threshold of 0.8 for best-N r². The x-axis ranges up to the number of tags obtained by best-N r² to cover every SNP with r² = 0.8. The purple horizontal dashed line indicates the full-SNP-set power achievable by genotyping the full set of SNPs.

Next, we consider all ten ENCODE regions and obtain similar results (Supplementary Figure 11). We report the fraction of SNPs required to achieve 95% of full-SNP-set power in each region (Supplementary Figure 12). The power-optimized method reduces the required number of tag SNPs by 60.0% compared to pairwise r² tagging and 20.9% compared to best-N r² on average over all populations and regions.

r² and power distribution

We examine the underlying reasons our power-optimized method achieves equivalent power using fewer tag SNPs than the r²-based methods. From the previous experiment in the ENr232 ENCODE region of the CEU population, we select three tag sets designed by each of power-optimized method, pairwise r² tagging, and best-N r². For each method, we select the smallest tag set which achieves the same 99% of the full-SNP-set power. These are 85 tag SNPs designed by power-optimized method, 123 tag SNPs designed by pairwise r² tagging, and 138 tag SNPs designed by best-N r². They have the almost same power of 86.2%, 86.3%, and 86.4% respectively. Pairwise r² tagging is designed with r² = 0.703.

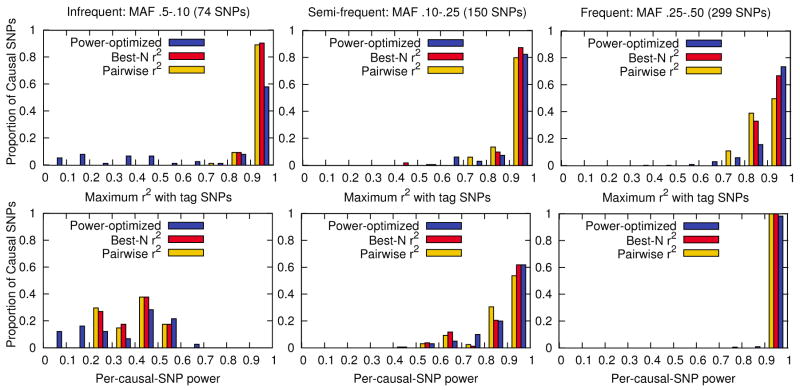
In order to analyze the performance of each tag set, we measure the tag set’s maximum r² to each putative causal SNP and the tag set’s power to detect each putative causal SNP (per-causal-SNP power). We group the causal SNPs into three groups based on their MAF: infrequent (5–10%), semi-frequent (10–25%), frequent (25–50%), which contain 74, 150, 299 SNPs respectively. We plot the r² and per-causal-SNP power distribution in Figure 2. In the infrequent group, the r² distribution of our power-optimized method is not very concentrated on the high level compared to the r²-based methods. In this group, the average r² of our power-optimized method is 0.75 while those of pairwise r² tagging and best-N r² are very high as 0.98 and 0.99 respectively. However, compared to the r² difference, the average power of our method is 36% which is not much lower than the 40% of the two r²-based methods. In the semi-frequent group, the average r² of power-optimized method is 0.94 which is slightly lower than 0.95 of the two r²-based methods, but the average power is 88% which slightly higher than 87% of the r²-based methods. In the frequent group, the average r² of our method, pairwise r² tagging, and best-N r² are 0.93, 0.91, and 0.94, and the average power estimates are 98%, 97%, and 98% respectively.

Figure 2.

Maximum r² and per-causal-SNP power distribution over all 533 causal SNPs in the ENr232 ENCODE region of the CEU population. We divide the causal SNPs into three groups by their MAF: infrequent (5%–10%), semi-frequent (10%–25%), frequent (25%– 50%), which contains 74, 150, 299 SNPs respectively. Each bar of different colors represent the power-optimized tagging method (85 tag SNPs), pairwise r² tagging method (123 tag SNPs), and best-N r² tagging method (138 tag SNPs). The three tag sets achieves the same 99% of full-SNP-set power.

The reason that in the infrequent or semi-frequent group our method achieves comparable or higher power with lower average r² is because our method takes into account MAF in selecting tag SNPs. If a causal SNP has a high MAF, the SNP is worth to cover with high r² because the power will significantly increase. If a causal SNP has a low MAF, the SNP might not be worth to cover with high r² because the power will still be low. In that case, we can allow the SNP to be covered with low r² without much power loss. Within a MAF group, our method strategically covers the SNPs of relatively high MAF with high r², thus having high power with low average r². This strategy is applied across MAF groups as well. Often, it can be possible to gain more power by spending a tag SNP to cover the SNPs in the frequent group than the SNPs in the infrequent group. Although our method has lower power than r²-based methods in the infrequent group, our method successfully covers SNPs in the semi-frequent and frequent groups with high r². Consequently, our method achieves the same average power with much fewer tag SNPs than pairwise r² tagging and best-N r², reducing the tag set size by 31% and 38% compared to those methods respectively.

We note that covering SNPs of high MAF with high r² is not the only behaviour of our method. If the per-causal-SNP power is saturated to 100%, then it can be possible to cover the causal SNP with moderate r² and still have 100% or very high power. In that case, our method strategically loosens the r² for that SNP so that it can spend the tag SNP for other SNPs which would increase power with high r². All these decisions are automatically made based on the average power increase.

Robustness

Our power-optimized tag SNP sets depend on the choice of study parameters such as relative risk and number of individuals. One concern with this approach is the potential for a performance drop due to using incorrect parameters. If the true relative risk is higher than expected, then some tag SNPs are wasted on common SNPs that already have very high power. If the true relative risk is lower than expected, then some tag SNPs are wasted on rare SNPs that are too difficult to capture even with higher r². We evaluate this performance drop with two experiments, and show that our method still performs better than or similarly to the r²-based methods in most cases. Both experiments are performed in the ENr232 ENCODE region of the CEU population.

In the first experiment, we design three different tag sets assuming relative risks of 1.1, 1.2, 1.4, and measure their power based on the assumption of a relative risk of 1.2. For each relative risk, we select 100 tag SNPs assuming 4,000 cases and 4,000 controls. For comparison, we design tag sets of the same size using pairwise r² tagging and best-N r². As shown in Figure 1, the two r²-based methods have similar power at this number of tag SNPs. Figure 3 shows the results. As expected, the tag set based on a correct relative risk (1.2) works better than the tag sets based on incorrect relative risks (1.1 and 1.4) at the number of individuals assumed in the design (4,000 cases and 4,000 controls). As the number of individuals decreases, the tag set based on a lower relative risk (1.1) shows the highest power amongst the tag sets. This is because lowering the number of individuals has the same effect on the test statistic as lowering the relative risk. For the same reason, as the number of individuals increases, the tag set based on a higher relative risk (1.4) obtains the highest power amongst the tag sets.

Figure 3.

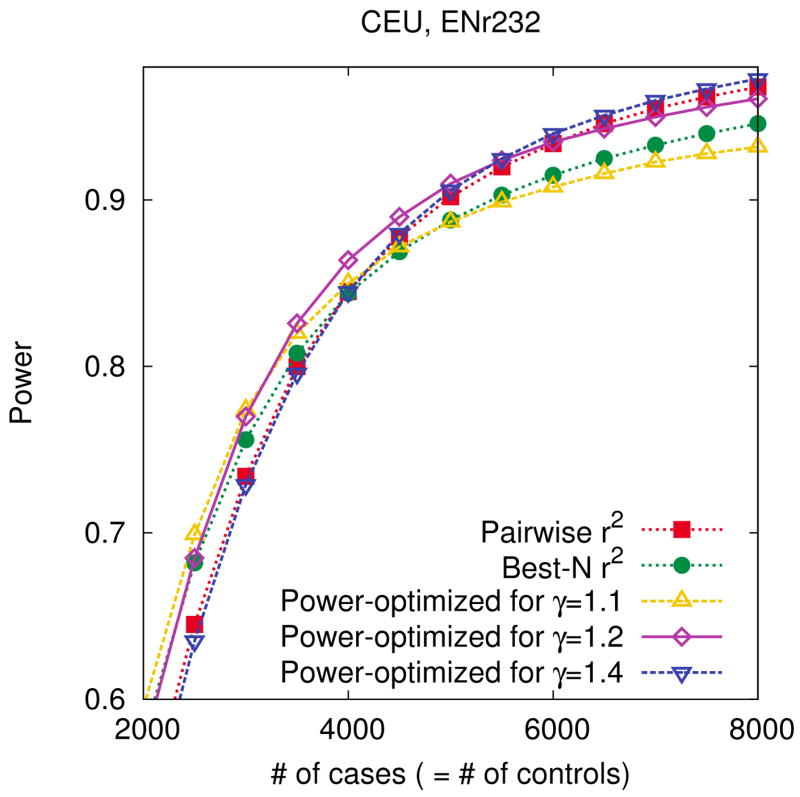
Robustness of our power-optimized method to errors of parameter selection. We use our power-optimized method to design three different tag sets of size 100 assuming different relative risks of 1.1, 1.2, 1.4 in the ENr232 ENCODE region of the CEU population. We also design two more tag sets of the same size using pairwise r² tagging and best-N r². We then measure the power of each tag set based on the assumption of a true relative risk of 1.2. We use a 5% region-wide significance level, a 5% MAF threshold for causal SNPs, and assume a disease prevalence of 0.01 and 4,000 cases and 4,000 controls when designing the tag sets.

At the number of individuals assumed in the design, even though r² is incorrectly assumed in the design, our method works similarly to the r²-based methods. If r² is correctly assumed in the design (line with diamond), even though the number of individuals varies, our method works similarly to the r²-based methods. Our method works comparably to the r²-based methods for a wide range of parameters, except for the extreme case that the bias of two parameters affect the statistic in the same direction, for example a smaller relative risk (1.1) is assumed in the design and a large number of individuals (8,000 cases and 8,000 controls) are used.

In the second experiment, we use the tag set based on a relative risk of 1.2 and the tag sets designed by r²-based methods from the previous experiment. We measure the power of the tag sets assuming 20 different relative risks from 1.0 to 1.5, and 160 different study sizes from 0 cases and 0 controls to 8,000 cases and 8,000 controls. Figure 4 shows the power difference between our method and r²-based methods over the two-dimensional parameter space (total 3,200 points). As expected, an optimal power gain is obtained when the parameters that the design is based on (=1.2 and 4,000 cases and 4,000 controls) or equivalent designs are applied (diagonal red curve). In this experiment, our method performs better than pairwise r² tagging when the actual effect size is smaller than assumed (lower left plane), and better than best-N r² when the actual effect size is larger than assumed (upper right plane). For both comparisons, our design works better than or similarly to the r²-based methods within a wide range of parameters.

Figure 4.

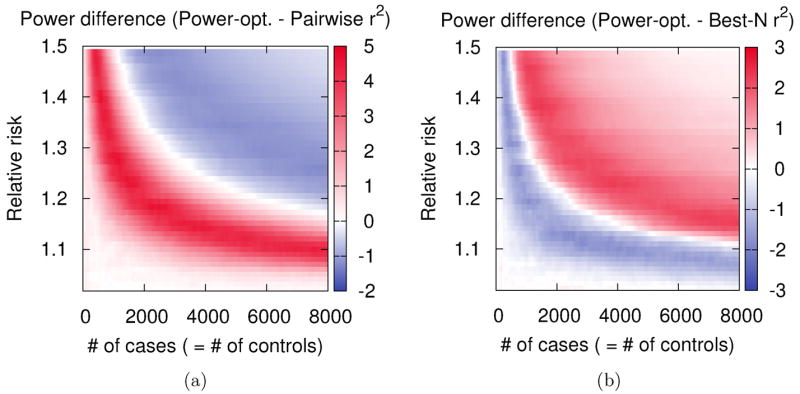
Distribution of power gain of our power-optimized method compared to r²-based methods over a parameter space. We design a tag set of size 100 assuming relative risk of 1.2 and 4,000 cases and 4,000 controls in the ENr232 ENCODE region of the CEU population. We also design tag sets of the same size using pairwise r² tagging and best-N r². We measure the three tag sets assuming many different parameters, varying the relative risk from 1.0 to 1.5 and the sample size from 0 case and 0 control to 8,000 cases and 8,000 controls. Then we plot the power difference (a) between our power-optimized method and pairwise r² tagging and (b) between our power-optimized method and best-N r², over the space of these various parameters. We use a 5% region-wide significance level, a 5% MAF threshold for causal SNPs, and assume disease prevalence of 0.01.

Varying study parameters such as relative risk, sample size, disease prevalence, and significance level can all be interpreted as varying the effect size, which can be thought of intuitively as the difference in the test statistic between the null and alternative hypothesis. Thus, the results of our experiments on varying the two major factors affecting the effect size (relative risk and sample size) can be straightforwardly generalized to the other parameters as well. Since the performance drop by using incorrect parameters exists, a study-independent method such as r²-based methods can be an appropriate design choice if the study parameters are completely unknown. But even when only the expected ranges of parameters are known, which we believe to be the case in current association studies, our method can provides robust performance.

Custom follow-up study design

After finding a putative association, a follow-up study verifies the association by replicating the result with independent samples. In many cases in follow-up studies, the samples are already in hand and have already been processed with a commercial product. A practical way to increase power is adding more tag SNPs to a commercial product by designing a custom SNP set.

We simulate a custom follow-up study by adding tag SNPs to the Affymetrix 500k chip in the ten ENCODE regions. For each region, assuming 4,000 cases and 4,000 controls, we incrementally add 5 tag SNPs to the tag set, and construct 100 different tag sets of increasing size. For comparison, we construct another 100 tag sets of similar size using pairwise r² tagging and best-N r².

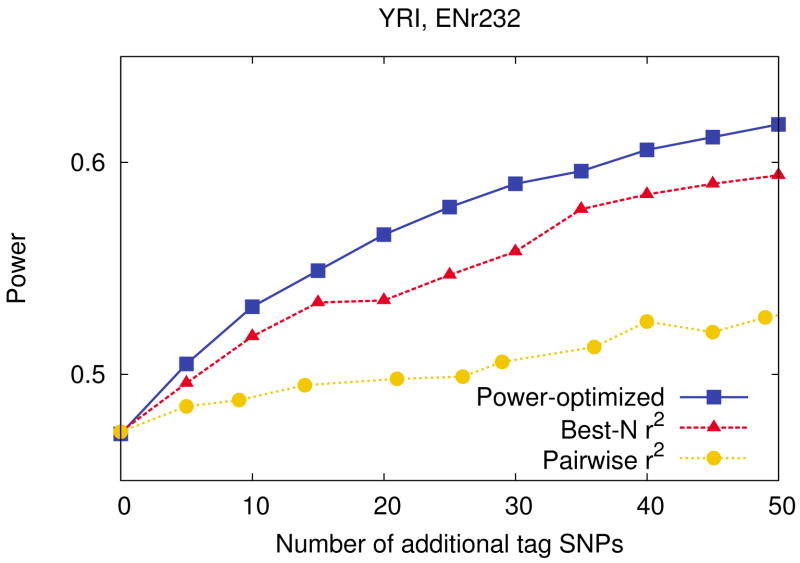
Figure 5 shows the power increase as we add more SNPs to the Affymetrix 500k chip in the ENr232 region of the YRI population. Adding tag SNPs in this region increases substantial power because the large number of SNPs (1,075) are not relatively well captured by the tag SNPs in the Affymetrix 500k chip (52 tag SNPs). Among the three methods, our method increases the most power. The results of the other populations and regions are similar and shown in Supplementary Figure 13. In the ENr232 region, by adding 1 SNP per 25kb (20 SNPs), our method improves power 6%, 10%, 10%, and 9% in the CEU, CHB, JPT, and YRI populations respectively, while pairwise r² tagging improves power 2%, 4%, 4%, and 3% and best-N r² tagging improves power 5%, 8%, 5%, and 6% in the same populations. The power gain by adding more tag SNPs varies between the regions depending on the coverage of the chip. For example, by adding 50 SNPs in the same YRI population, we get a 6% and 7% power increase in the ENm013 and ENm014 regions, while we get a 17% and 15% power increase in the ENm010 and ENr232 regions. Therefore, it is important to examine the coverage of the commercial chip for the region of interest, to see if we will get sufficient power by adding more SNPs. Since our design framework provides efficient empirical simulation for measuring power as well as an efficient tag SNP selection method, we can accurately evaluate power before and after adding tag SNPs, and decide which SNPs to add. Our method can provide optimal performance in custom follow-up study designs because the value of the relative risk can be estimated from the result of original study.

Figure 5.

Power comparison between our power-optimized method and r²-based methods with respect to the number of tag SNPs added to a commercial chip. To simulate a custom follow-up study, we use each of our power-optimized method, pairwise r² tagging, and best-N r², to add tag SNPs to the tag set defined by the Affymetrix 500k chip in the ENr232 ENCODE region of the YRI population. We use a 5% region-wide significance level, a 5% MAF threshold for causal SNPs, and assume relative risk of 1.2, disease prevalence of 0.01, and 4,000 cases and 4,000 controls.

High-throughput genotyping product design

Since our power-optimized tagging method can scale to the whole genome, we can apply the method to design a whole genome high throughput genotyping product. For each of the HapMap populations, we design 500k, 300k, 100k whole genome tag sets using our power-optimized method assuming 8,000 cases and 8,000 controls. We also design the same size of tag sets using pairwise r² tagging and best-N r². Figure 6 (CEU) and Supplementary Figure 14 (all populations) show that our tag sets outperform the r²-based tag sets.

Figure 6.

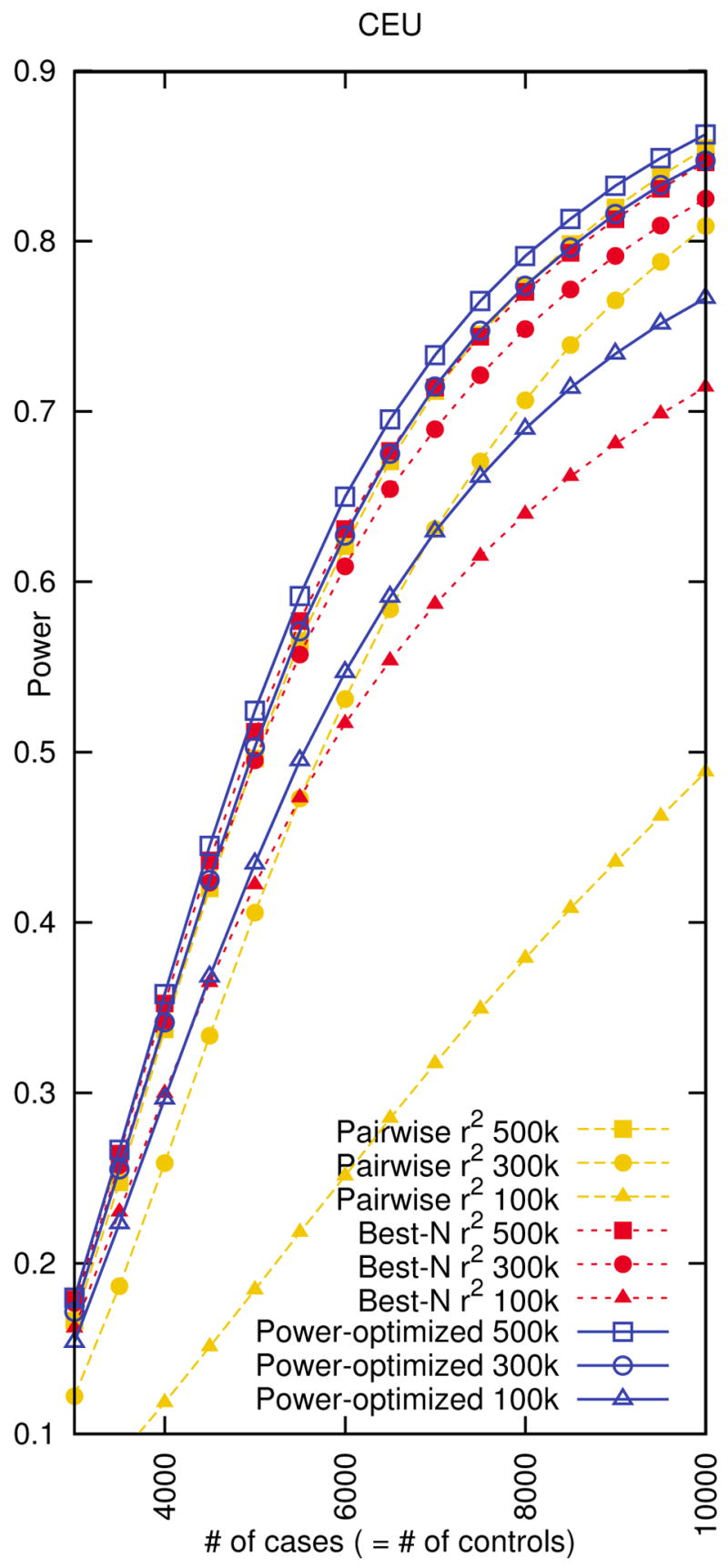
Genome-wide power comparison between whole genome tag sets designed by our power-optimized method, pairwise r² tagging, and best-N r² in the CEU population. We measure the power assuming relative risk of 1.2, disease prevalence of 0.01, a 5% genome-wide significance level, and a 5% MAF threshold for causal SNPs. We use 8,000 cases and 8,000 controls when designing the tag sets.

We also compare our tag sets to commercial products. Figure 7 (CEU) and Supplementary Figure 15 (all populations) show that our tag sets work better than the commercial products of the same size. Our 100k tag set performs similarly to the Affymetrix 500k chip in the CEU and JPT+CHB populations, but performs worse in the YRI population, because 100k tag set is not large enough to capture the variations in the YRI population. Our 100k tag set also performs similarly to the Illumina 300k chip, except in the CEU population for which Illumina 300k chip seems to be optimized. Our 300k tag set performs better than or comparable to any commercial product evaluated including the Illumina 550k chip, and our 500k tag set outperforms all products in all populations. For the same 80% genome-wide power level, our 500k tag set requires 26%, 29%, and 33% fewer individuals than the Affymetrix 500k chip and 7%, 11%, and 23% fewer individuals than the Illumina 550k chip in each of the CEU, JPT+CHB, YRI populations.

Figure 7.

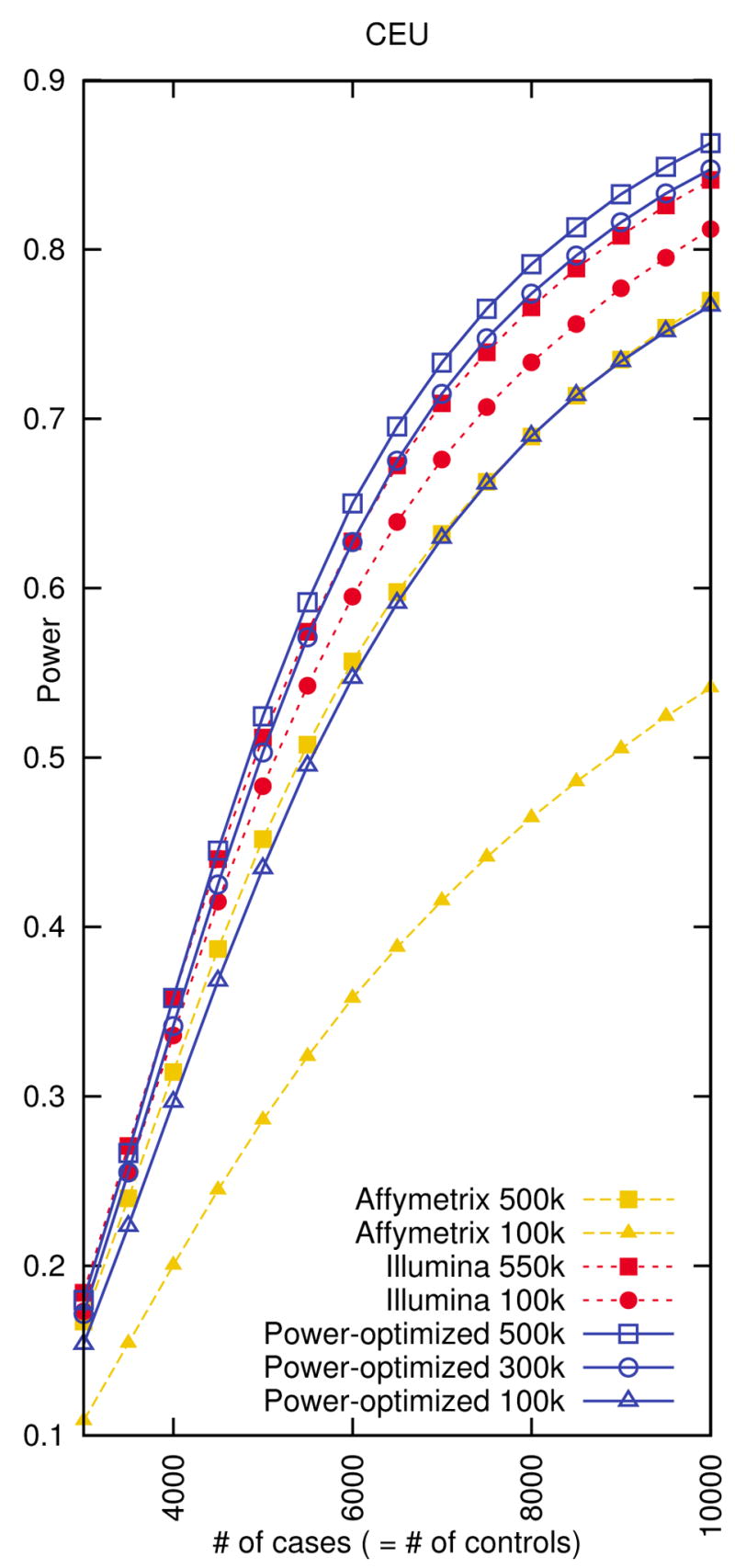
Genome-wide power comparison between whole genome tag sets designed by our power-optimized method and the commercial products in the CEU population. We measure the power assuming relative risk of 1.2, disease prevalence of 0.01, a 5% genome-wide significance level, and a 5% MAF threshold for causal SNPs. We use 8,000 cases and 8,000 controls when designing the tag sets.

Efficient power estimation

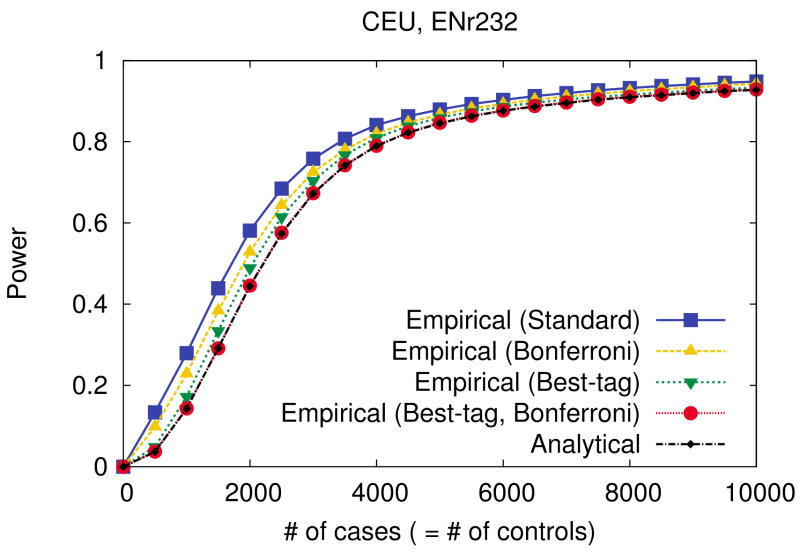
The analytical approximation for power that we use in design is efficient enough to estimate the whole genome power of a 500k tag set in 3 minutes. This efficiency allows us to design on one ENCODE region in 3 seconds and on the whole genome in 1.5 CPU hours using the adjusted greedy algorithm (See Methods). An underlying reason we use an analytical approximation instead of more accurate empirical simulation, other than the computational feasibility, is that we only need a rough estimate of the power to select tag SNPs. The analytical approximation always underestimates power yet in the vast majority of cases preserves the relative ordering of candidate tag sets with respect to their power. However, an analytical approximation is overly inaccurate for the final estimate of the power of a design, because it applies two assumptions which ignore the correlation structure between SNPs. The Bonferroni assumption ignores the correlation structure between tags by assuming they are independent for multiple-hypothesis correction. The best-tag assumption ignores the correlation structure between a causal SNP and multiple tags by assuming a causal SNP is detected only by its best tags, disregarding the possibility that other tags can also detect the causal SNP. We measure the effects of these assumptions on power. Given a fixed tag set defined as the common SNPs in the Illumina 550k chip, we perform empirical simulations for measuring power with all four combinations of the two assumptions (Bonferroni and best-tag) and compare the results to the analytical approximation. Details of how we incorporate these assumptions into the simulations are described in Methods.

Figure 8 (ENr232, CEU) and Supplementary Figure 16 (other regions) show that we can underestimate the power by up to 15% using both assumptions. The effect of the best-tag assumption is shown to be more critical than the effect of the Bonferroni assumption in our results. The difference between the effects of two assumptions is most significant in the YRI population. The small effect of the Bonferroni assumption implies that the tag SNPs are nearly independent due to the short LD in the YRI population. The significant effect of the best-tag assumption implies that there are many ungenotyped SNPs which are correlated to multiple tag SNPs with moderate r². (If a SNP is directly genotyped or highly correlated to a tag SNP, then the effect of the best-tag assumption is small.) From the same reasoning, we can expect that as we collect more and more tag SNPs, the effect of the Bonferroni assumption will increase and the effect of the best-tag assumption will decrease (but not disappear entirely). The empirical simulation with both assumptions (red circles) is almost equivalent to the analytical approximation (black small diamonds) showing that the significant difference in power between the empirical simulation and the analytical approximation is directly due to the assumptions and not the stochastic nature of simulation.

Figure 8.

Comparison between four different empirical estimates of power and the analytical approximation in the ENr232 ENCODE region of the CEU population. Given a tag set consisting of the common SNPs in the Illumina 550k chip, we perform empirical simulations with all four combinations of the best-tag and Bonferroni assumptions, and compare to the analytical approximation. Details of how we incorporate these assumptions into our simulations are described in the Methods. We use a 5% region-wide significance level, a 5% MAF threshold for causal SNPs, and assume relative risk of 1.2 and disease prevalence of 0.01.

After design, we run empirical simulations for measuring power to avoid the inaccuracy of the analytical approximation. This resampling approach using reference data set is originally described by de Bakker et al. (2005). We improve the efficiency of this procedure and scale it to the whole genome using a random sampling procedure. If we directly apply the standard simulation to the whole genome to measure the power of the Affymetrix 500k chip for 4,000 cases and 4,000 controls in the CEU population, it takes 4,000 CPU hours to construct null and alternate panels. Using our improved simulation procedure, it takes less than 10 CPU hours for the same construction.

Discussion

We introduced a design framework which provides an efficient tag SNP selection method based on power and a quick empirical simulation procedure that can accurately measure the power of a tag set. The tag SNP selection and the empirical simulation can efficiently scale to the whole genome. Our framework efficiently finds the “key” tag SNPs contributing to power thus providing superior performance to the widely used r²-based methods in both custom follow-up study design and whole genome tag set design.

We assumed a fixed relative risk of 1.2 for all causal SNPs, since the fixed relative risk assumption is often more realistic than the varying relative risk when we can approximate the relative risk before the study. Our method can maximize power under the varying relative risk assumption as well. We assumed a multiplicative disease model, but the same tag SNP selection technique based on other disease inheritance models can be straightforwardly developed. Furthermore, our method can be optimized over multiple parameters.

For example, if we want to design a study optimized for both relative risks of 1.2 and 1.4, we can select tags to maximize the average power over these two disease models. This approach will expand the robustness of our method over a wider range of parameters, at the expense of the peak performance at the single disease model and parameters used in the design. If the study parameters are completely unknown, a study-independent measure such as r² can be a suitable choice. However, since many current association studies have at least an expectation of the ranges of parameters, in that case, our method can provide superior performance over the r²-based methods. A good example is a custom follow-up study, where the relative risk is estimated from the original study.

The results show that our whole genome tag set works significantly better than the commercial products. This comparison is unfair because we designed a tag set for each population while the commercial products are designed for multiple populations. Howie et al. (2006) propose an r²-based tag SNP selection method for multiple populations. Our method can also select tag SNPs for multiple populations, by maximizing the sum of the power over multiple populations (Σp_i where p_i is the power for population i). However, this might bias against populations that have low power such as the YRI population. We can avoid this problem by heuristically adding second-order terms to penalize the bias toward a specific population (Σp_i +Σp_ip_j). We found that tag sets designed for multiple populations in this way have similar power in each of the populations to a tag set designed for a single population (data not shown).

The computational core of our tagging method is an efficient procedure for selecting tag SNPs given a fixed number of individuals and a fixed number of tags. Since this core procedure is very efficient we can answer many design questions by repeatedly searching with this core procedure and by using our efficient empirical simulation for accurately measuring power. For example, our method can answer questions such as “How many additional tags do we need to achieve 80% power given a sample size in addition to the Affymetrix 500k chip for a candidate region?”, “If we use the individual genotyping for a small region of interest, what is the optimal cost point between the number of individuals and number of tags given a desired power of 80%?” (Pardi et al., 2005) or “How many individuals should we collect for 70% genome-wide power when using the Illumina 550k chip?”.

Our experiments for custom follow-up study design are performed in the context of replication analysis of a genomic region of interest without prior knowledge. In addition, our method can leverage the results from previous studies by either explicitly including prioritized tag SNPs or by applying a weighted prior of causal SNPs obtained from previous studies (Yu et al., 2007; Eskin, 2008). Our method can also be extended to maximize the power of joint analysis combining the original and the replicated data sets (Skol et al., 2006). Furthermore, our method can be easily modified to maximize the minimum power over all causal SNPs instead of the average power.

A recent methodological development in statistical genetics allows us to estimate the probability distribution of ungenotyped SNPs given a tag set and directly compute the test statistic from the distribution. This is called imputation or multi-marker analysis (Zaitlen et al., 2007; Marchini et al., 2007). Since the test statistic is based on estimated information which also has an uncertainty (variance), the multiple hypothesis correction is more subtle. To the best of our knowledge, there is no established tag SNP selection method for this analysis. Our method can be applied to this multi-marker analysis in two different ways. First, we can select tag SNPs to maximize the imputed power at each step. The computational cost of this procedure will be very high. Second, we can design a tag set assuming a single marker analysis, and then apply multi-marker analysis to the resulting tag set. We assume that this latter approach will work reasonably well, since we expect that if a tag set has a good power in a single marker analysis, in most cases it will also have a good power in a multi-marker analysis. We expect that tag SNP selection for imputation analysis will be an active area of research in the future.

In summary, we present an efficient and accurate power-optimized design framework which also provides exibility and robustness. The utility of our method ranges from custom follow-up study designs to whole genome high-throughput product design. Our method is publicly available for research purposes via web server at http://design.cs.ucla.edu.

Materials and Methods

Power-optimized tag SNP selection

Our power-optimized tag SNP selection method is a stepwise greedy procedure to maximize power. We assume that we can estimate the relative risk (γ). We determine the MAF threshold and the significance level α. Then, we fix at least one degree among the three degrees of freedom in design which are (1) the number of individuals, (2) number of tags, and (3) desired power. If we fix two of them, our method will give one design. If we fix one of them, our method will iterate and give many designs to choose among. The computational core of this procedure is selecting tags to maximize power given the fixed numbers of individuals and tags. Since this core procedure is very efficient, our method can quickly iterate to find the solution for any choice of fixed parameters. For example, if we fix the desired power, our method will use binary-search over the number of individuals by repeating the core procedure until the resulting tag set meets the desired power. It will iterate this whole process for every number of tags.

For simplicity, we will only consider the core tagging procedure where both the numbers of individuals (N) and the number of tags (n_t) are fixed. Let S be the set of all SNPs in the region. Let C ⊆S be the set of (common) putative causal SNPs defined by the MAF threshold. Let I ⊆ S and E ⊆ S be the sets of SNPs that we want to include into or exclude from the tag set. Then our tagging procedure is as follows.

1. Initialize the tag set as T ← I

2. For every candidate tag SNP x ∈ S − (T ∼ E), analytically estimate per-causal-SNP power for every causal SNP c ∈ C using the tag set T ∼ {x}, to get the average power P(T∼{x}).

3. Select the best candidate tag SNP x′ which maximizes P(T∼{x′}).

4. T ← T ∼{x}

5. Repeat from step 2 while [T]< n_t

A more detailed pseudo-code is shown in Supplementary Figure 9. How we analytically estimate the per-causal-SNP power given a tag set at step 2 will be described below. During the procedure, we measure the average power of a tag set for O(n_cn_t) times where n_c and n_t are the number of causal SNPs and tag SNPs respectively. Since empirically measuring power through simulation for this number of times is computationally impractical, we use an analytical approximation for power.

For genome-wide design, we assume the maximum distance of LD to be 250kb and use the adjusted greedy algorithm (Supplementary Figure 10) to reduce the computational burden. 250kb is not long enough to capture long range LDs, but enough for selecting tag SNPs based on power. We will assume a longer range of maximum LD (10Mb) when we estimate the power of a design using empirical simulation. The adjusted greedy algorithm picks k “independent” SNPs at each round, from the top of the candidate tag SNP list sorted by their power increase. We define two SNPs to be independent if the distance between them is greater than the twice the length of maximum distance of LD. We set k to be 1% of the total number of SNPs. We consider the power between a tag SNP and a causal SNP only if the r² between them is ≥0.1.

We now describe how to analytically estimate the per-causal-SNP power of a tag set at step 2 of the tagging procedure. We use the framework of Pritchard & Przeworski (2001); Jorgenson & Witte (2006); Klein (2007); Eskin (2008). Given an association study which collects genotypes in N⁺=2 case and N⁻=2 control individuals (equivalently N⁺ and N⁻ chromosomes), we assume that a marker A with population minor allele frequency p_A affects the disease with relative risk γ. Let F be the disease prevalence. The case and control allele frequencies are then

$$p_A^{+}=\frac{\gamma p_A}{(\gamma -1)p_A+1}\text{and}{p}_A^{-}=\frac{p_A-F{p}_A^{+}}{1-F}(\text{or},p_A^{-}\approx p_A\text{ if }F\text{ is very small})$$

respectively. We denote the observed case and control frequencies in the collected sample as ${\widehat{p}}_A^{+}$ and ${\widehat{p}}_A^{-}$. The association statistic at marker A,

$$S_A=\frac{{\widehat{p}}_A^{+}-{\widehat{p}}_A^{-}}{\sqrt{{\widehat{p}}_A^{\pm }(1-{\widehat{p}}_A^{\pm })}}\sqrt{\frac{N^{+}{N}^{-}}{N^{+}+N^{-}}}(\text{where}{\widehat{p}}_A^{\pm }=({\widehat{p}}_A^{+}+{\widehat{p}}_A^{-})/2)$$

approximately follows a normal distribution with variance 1 and mean (non-centrality parameter)

$${\lambda }_A=\frac{p_A^{+}-p_A^{-}}{\sqrt{p_A^{\pm }(1-p_A^{\pm })}}\sqrt{\frac{N^{+}{N}^{-}}{N^{+}+N^{-}}}\text{. }(\text{where}{p}_A^{\pm }=(p_A^{+}+p_A^{-})/2)$$

If we genotype a marker B correlated with A with a correlation coefficient of r_AB, the power that the marker B will be detected as significant is analytically approximated as

$$P_B=1-\frac{1}{\sqrt{2\pi }}{\int }_{{\mathrm{\Phi }}^{-1}(\alpha /2)+{\lambda }_A\sqrt{r_{AB}^2}}^{{\mathrm{\Phi }}^{-1}(1-\alpha /2)+{\lambda }_A\sqrt{r_{AB}^2}}{e}^{-\frac{1}{2}{x}^2}dx$$

with respect to the significance threshold α, where Φ(x) is the c.d.f. of the standard normal distribution.

Now we can estimate the single marker power between the causal SNP A and the tag SNP B. To extend this single marker power to multiple markers, we apply two simplifying assumptions. A best-tag assumption assumes that each causal SNP is only detected by its best tag, that is, the most correlated tag SNP with the highest r². A Bonferroni assumption assumes that every SNP is independent allowing us to use α=n_t as a significance level for a single test where α is the region-wide significance level and n_t is the number of tags (the Bonferroni correction). With these two assumptions, the per-causal-SNP power for each causal SNP is efficiently computed as the single marker power that the best tag SNP will be detected as significant. Thus, the average power can be analytically estimated by averaging the per-causal-SNP power over every causal SNP.

r²-based tag SNP selection

Pairwise r² tagging (de Bakker et al., 2005; Carlson et al., 2004b; HapMap, 2003, 2005) is a widely used r²-based tag SNP selection method that greedily chooses the smallest number of tag SNPs with a minimum r² threshold between tag SNPs and uncollected SNPs. The procedure starts with a SNP pool containing every SNP of interest, which is defined by MAF ≥5% in our experiments. At each step, the procedure selects a tag SNP which covers the most SNPs in the pool with the r² threshold, and removes the tag SNP and the SNPs it covers from the pool. Then the procedure is repeated until the pool becomes empty. Since the only parameter we can vary in pairwise r² tagging is the r² threshold, we use binary-search over the threshold when we want to design a specific tag set size, with the precision of 0.001. For the follow-up study design which adds SNPs to a pre-defined tag set, we first remove from the pool the pre-defined tag SNPs and the SNPs they cover, and then resume the normal procedure. For the genome-wide study design, as in our power-optimized method, we assume 250kb as the maximum distance of LD and use the adjusted greedy algorithm. The algorithm picks k “independent” SNPs at each round, from the top of the candidate tag SNP list sorted by the number of SNPs they cover. We define two SNPs to be independent if the distance between them is greater than the twice the length of maximum distance of LD. We set k to be 1% of the total number of SNPs.

Best-N r² (de Bakker et al., 2005) is another r²-based method. The procedure is the same as pairwise r² tagging except that the tag SNPs are selected until the desired tag set size is obtained, not until the SNP pool becomes empty. Thus, the tag set size can be controlled without varying the r² threshold. We use a fixed r² threshold of 0.8 in our experiments. For genome-wide design, we use the same assumption of maximum distance of LD and the adjusted greedy algorithm as for pairwise r² tagging.

Empirical simulation for power

We empirically measure the final estimate of the power of a tag set after design. Our empirical simulation is based on the standard simulation procedure described by de Bakker et al. (2005). This procedure resembles the “bootstrapping” statistical procedure which samples from the data set with replacement to estimate the sampling distribution of an estimator (Wasserman, 2004; Efron, 1979). The major difference is that a typical bootstrapping procedure draws the same number of samples as the data set, while de Bakker et al. (2005)’ s simulation amplifies the number of samples based on a small reference data set, which is the HapMap. This procedure assumes that although the currently available reference data set is small, the correlation structure between SNPs will be mostly conserved independent of the size of the data set. Since this procedure does not require the conservative assumptions used in the analytical approximation, it is a standard method for measuring power (de Bakker et al., 2005; Marchini et al., 2007).

The procedure consists of creating null panels and alternate panels. Random chromosomes are drawn from the reference data set to create many case/control panels without any causal association (null panels). For each null panel, the best χ² statistic among all tag SNPs is obtained. Given a region-wide significance level α, the maximum χ² value exceeded in α of null panels is chosen as the threshold to declare a positive result. Next, based on the assumption of a causal SNP which defines the expected allele frequencies in cases and controls, random chromosomes are drawn from the reference data set to create many case/control panels (alternate panel). For each alternate panel, a positive result is recorded if the best χ² statistic among all tag SNPs exceeds the χ² threshold obtained in the null panels. The power is estimated as the proportion of the positive findings among alternate panels. Previous studies (de Bakker et al., 2005; Pe’er et al., 2006; Zaitlen et al., 2007) assume a uniform distribution for the causal SNP, and construct an even number of panels per every putative causal SNP.

This standard simulation is not based on the best-tag or Bonferroni assumption, but we can incorporate these assumptions into the simulation for the purpose of comparison (Figure 8 and Supplementary Figure 16). The Bonferroni assumption is incorporated by using the Bonferroni correction instead of null panels to assess the per-marker threshold. The best-tag assumption is incorporated by declaring a positive result in an alternate panel only when the causal SNP’s most correlated tag shows significance, regardless of other tags.

The computation cost of empirical simulation is a major bottleneck of optimal design of association studies. We improved the efficiency of empirical simulations by taking advantage of having small reference samples. Instead of drawing each simulated cases and controls from the reference samples, we count how many times each chromosome in reference samples are drawn in cases and controls. Since the number of reference samples are typically much smaller than the number of individuals in the simulation, such an implementation improves the efficiency of simulation studies in orders of magnitudes than the straightforward implementation. With r simulation panels, N individuals and t tags, the computational complexity is reduced from O(rNt) to O(r(N+t)) assuming the number of reference panel is a constant smaller than N.

To the best of our knowledge, no one has applied this standard simulation to the whole genome. We introduce two ideas to efficiently scale it to the whole genome. First, we observe that the SNPs very far away from the causal SNP have the same distribution as null panels. Thus, positive results found on those SNPs are likely to be false positives. We use this insight to set a maximum distance L between a casual SNP and a tag SNP, to avoid having to generate alternate panels consisting of entire chromosome. We conservatively choose L=10Mb not to miss any long range correlation. This idea reduces the computational load of alternate panel construction by more than 5-fold. Second, we introduce a sampling procedure. The standard strategy of creating an even number (k) of panels per every putative causal SNP (even-k strategy) is impractical for the whole genome even when k = 1. Instead, we sample the causal SNP from the uniform distribution, and create a number of panels per each sampled causal SNP (sample-k strategy). We analyze the variance of the power estimate in this strategy to determine the number of sampling iterations. Using the sampling strategy, the variance of the average power estimate is approximately given as 3p(1−p)=m where p is the true average power and m is the number of samplings (See Supplementary Materials). Thus, the number of samplings can be estimated given a desired accuracy. The idea of sampling reduces the computational load by more than 20-fold compared to a naive even-k strategy which constructs one panel per causal SNP.

These two ideas for efficient genome-wide simulation increase the efficiency of alternate panel construction but do not help the null panel construction where a causal SNP is not defined. We can reduce the computational load in the null panel construction by adjusting the number of individuals to an appropriate level, based on the fact that the adjusted χ² threshold is independent of the number of individuals when the number of individuals is large (Conneely & Boehnke, 2007). This fact allows us to construct null panels once and use it for many different numbers of individuals. We construct null panels of 1,000 cases and 1,000 controls when we measure the power of designs in our experiments.

Genotype data

We downloaded the HapMap genotype data (build 36) for the whole genome and ENCODE regions from the HapMap project web site (HapMap, 2005). The project collected SNP information from 30 trios in each of the African (YRI) and the European (CEU) populations, and 45 unrelated individuals in each of the Japanese (JPT) and Chinese (CHB) populations. The data includes 2,605,595, 2,471,887, and 2,926,893 polymorphic SNPs in each of the CEU, JPT+CHB, and YRI populations. We phased the data into haplotypes using the HAP(Zaitlen et al., 2005) software.