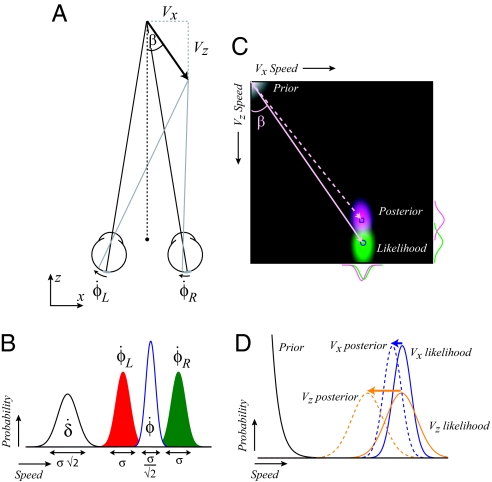
Fig. 1.
Illustration of binocular viewing geometry and the Bayesian model. (A) A movement at angle β can be described by a lateral component, Vx, and a motion-in-depth component, Vz. The movement produces excursions at the two eyes: φ̇L, φ̇R. For illustration, the vectors are shown as retinal motions; however, eye rotation signals in combination with retinal motion are likely used by the brain. (B) Hypothetical probability distributions for the retinal motion vectors φ̇L, φ̇R. The distributions have equal, but independent, noise (σ). The SD of the difference signal is twice that of the mean signal. These differential reliabilities influence the reliability with which Vx and Vz are estimated. (C) A depiction of the Bayesian model shows the prior (depicted in white/gray in the top left-hand corner), the likelihood distribution (green), and the posterior distribution (purple). The variability of the likelihood is greater in the Vz than Vx direction, meaning that the prior has a differential influence. The angle estimated on the basis of the maximum of the posterior distribution (dotted mauve line) is more eccentric than that specified by the likelihood (solid mauve line). The square and circular markers represent the peak of the posterior and likelihood distributions respectively. (D) An illustration of the Bayesian model. The likelihood distribution is more variable in the Vz dimension than the Vx dimension, meaning that the posterior is more influenced by the prior in the Vz dimension. The differential biasing effect of the prior results in biased estimates of trajectory (β) when Vx and Vz are contrasted.