Perception of speech reflects optimal use of probabilistic speech cues

Abstract

Listeners are exquisitely sensitive to fine-grained acoustic detail within phonetic categories for sounds and words. Here we show that this sensitivity is optimal given the probabilistic nature of speech cues. We manipulated the probability distribution of one probabilistic cue, Voice Onset Time (VOT), which differentiates word-initial labial stops in English (e.g., “beach” and “peach”). Participants categorized words from distributions of VOT with wide or narrow variances. Uncertainty about word identity was measured by four-alternative forced-choice judgments and by the probability of looks to pictures. Both measures closely reflected the posterior probability of the word given the likelihood distributions of VOT, suggesting that listeners are sensitive to these distributions.

Introduction

The goal of speech perception can be characterized as finding the most likely intended message given a noisy acoustic signal. Any two minimally different speech categories (e.g., words, syllables, phones or features) may vary along several dimensions, with each dimension characterized by one or more acoustic-phonetic cues. These cues are highly variable due to a variety of speaker-specific (e.g. Johnson, Ladefoged & Lindau, 1993; Perkell, Zandipour, Mattheis & Lane, 2002) and context-specific factors (e.g. Moon & Lindbloom, 1994; Fougeron & Keating, 1997; Wouters & Macon, 2002), are variable even when individual words are produced by a single speaker in a consistent context in a laboratory setting, and this variability seems to be roughly normally distributed (Newman, Clouse, & Burnham, 2001; Allen, Miller & DeSteno 2003). Thus when perceiving speech, listeners are dependent on inherently probabilistic evidence (acoustic-phonetic cues produced by the speaker) to make judgements about events in the world (intended categories of the speaker). The goal of the current paper was to assess whether listeners behave as “ideal observers” when using probabilistic acoustic information to recognize words.

Ideal observer models are increasingly being applied to perception in many domains and at multiple levels (e.g. Anderson, 1990; Griffiths & Tenenbaum, 2006; Barlow, 1957; Geisler, 1989; Todorov, 2004). In these models, decisions about perceptual information are guided by several basic principles that guarantee that decisions will be optimal. The first principle is to acknowledge that the world provides only probabilistic information, which is inherently ambiguous at any given time. A second principle is that decisions should be made using all the available information. In order to take full advantage of probabilistic information these models use the entire probability distribution for each information source and each source is weighted according to its precision. The prediction for speech perception is that listeners should be sensitive to the entire probability distribution of acoustic-phonetic cues for a word and the precision or amount of certainty about a word that a particular cue provides should be inversely proportional to the variance of that cue for that word.

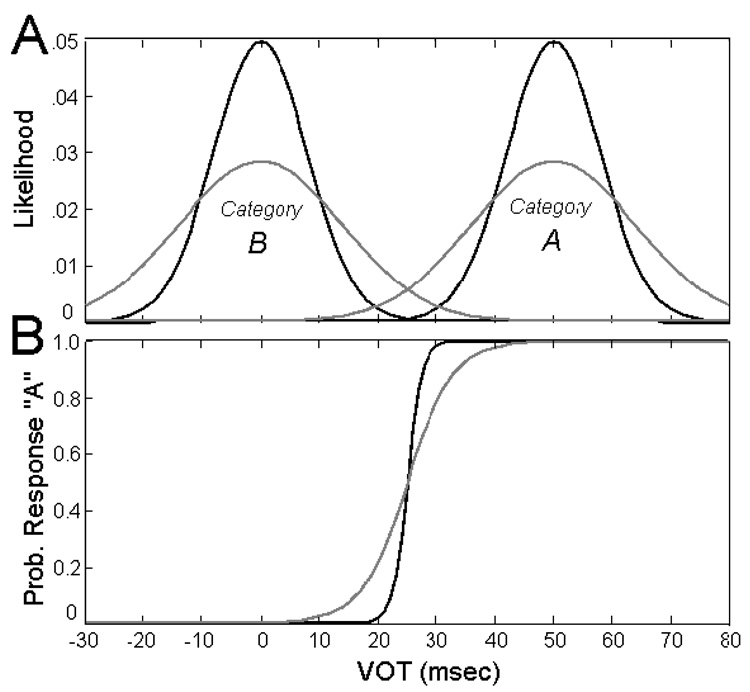
The probability distribution of an acoustic-phonetic cue for a particular word or speech category is the number of times each value of the cue has occurred as a member of that category. Figure 1a shows hypothetical probability distributions for categories differing along a particular acoustic-phonetic dimension, Voice Onset Time (VOT). The darker lines correspond to categories which are produced more consistently and thus have narrower distributions; the lighter lines to categories produced less consistently with wider distributions. Both pairs of distributions represent situations where an acoustic phonetic cue (VOT) is available to distinguish between two categories (A and B). The means of the distributions are the same distance apart but the variances differ. If listeners are acting as ideal observers, the increased overlap in the distributions with greater variance (lighter lines) will result in increased uncertainty (decreased precision) about which category they are hearing.

Figure 1.

[A] Probability distributions of tokens that listeners categorized in the narrow condition (dark lines) and wide condition (light lines). [B] Optimal response curves calculated from the probability distributions using Equation (1) for the narrow condition (dark lines) and wide condition (light lines).

To formalize this prediction, we define the task of the listener as determining for a particular token, stimX, the probability it came from category A (P(categoryA|stimX)). The optimal solution is given by (1) where P(stimX|categoryA) is the probability distribution of cue X for category A.

$$P(\mathit{\text{category}}A|\mathit{\text{stim}}X)=\frac{P(\mathit{\text{stim}}X|\mathit{\text{category}}A)}{P(\mathit{\text{stim}}X|\mathit{\text{category}}A)+P(\mathit{\text{stim}}X|\mathit{\text{category}}B)}$$ (1)

Equation 1 is a simplification of Bayes’ rule that ignores the role of prior probabilities for each category (i.e., all categories are equally likely), a point we return to later. In the optimal solution, then, the posterior probability of a particular category given an acoustic phonetic cue (P(categoryA|stimX)) is proportional to how often that cue value has occurred with that category in the past (P(stimX|categoryA)), relative to how often it has occurred with any category (P(stimX|categoryA) + P(stimX|categoryB)). The optimal solution for each of the pairs of distributions in Figure 1a is illustrated in Figure 1b. Note that for both solutions the category boundary (point where the function crosses 0.5) is in the same place along the x-axis, but the slopes of the categorization functions differ, reflecting the increased uncertainty in the case of the wide distributions. If listeners are making decisions using the entire probability distributions, we predict different categorization slopes for different amounts of category variance (overlap). Furthermore the ideal observer model makes a quantitative prediction about the amount of uncertainty (slope of the categorization function) given the amount of overlap (variance of the probability distributions). This describes the minimal amount of uncertainty for an ideal observer. We also expect some amount of additional uncertainty for actual observers in both situations due to internal and external noise in estimating the probability distributions. This additional uncertainty should not depend on the specific distributions of the cues and should be the same for observers categorizing both pairs of distributions.

Fine grained sensitivity to acoustic-phonetic cues is required for listeners to track the distributions of acoustic-phonetic cues. Early models of speech perception treated within-category variance as noise. Mechanisms such as categorical perception were thought to define ideal boundaries along a continuum, with all exemplars within those boundaries treated as identical category members (Liberman, Harris, Hoffman, & Griffith, 1957, Liberman 1996). However, considerable evidence has accumulated that listeners are sensitive to within-category differences. For example, differences in: reaction time (Pisoni & Tash 1974), category goodness ratings (Miller & Volaitis, 1989), degree of semantic priming (Andruski, Blumstein, & Burton, 1994), patterns of eye movements (McMurray, Aslin & Tanenhaus, 2002), and neural patterns of activity (Blumstein, Myers, & Brisman, 2005) have all been documented for within-category VOT differences. In addition both infants and adult listeners use distributional information to find the number of categories along a continuum (Maye & Gerken, 2000; Maye, Werker & Gerken, 2002; Maye, Weiss & Aslin, 2008) and the optimal boundary between categories (Clarke & Luce, 2005). These results are consistent with an ideal observer model. What has thus far not been shown, however, is that listeners are sensitive to the entire probability distribution of an acoustic-phonetic cue, and in particular the variances as predicted by equation (1).

We tested this hypothesis by manipulating the probability distributions of tokens along a VOT continuum in a category judgement task. In English, VOT (the time between the release burst and the onset of voicing in the vowel) is the dominant cue to voicing (Lisker & Abrahmson, 1964) in word initial position. Short VOTs correspond to words such as “beach” and long VOTs to words such as “peach”. The stimuli were tokens from two probability distributions (shown in Figure 1a) centered around 0ms and 50ms (the prototypical category means for “beach” and “peach” in American English). For one group of participants, stimuli came from a pair of distributions with relatively wide variance (14 ms), and for another group, stimuli came from a pair of distributions with relatively narrow variance (8 ms). Importantly both pairs of distributions contain the same number of tokens overall and the same category means. Participants categorized the stimuli by clicking on the picture they thought was appropriate (e.g., a peach). Each trial was both a test and a training trial; there were not separate training and testing phases. Using equation (1), we predicted the probability that listeners would choose the peach for each step along the VOT continuum (Fig. 1b).

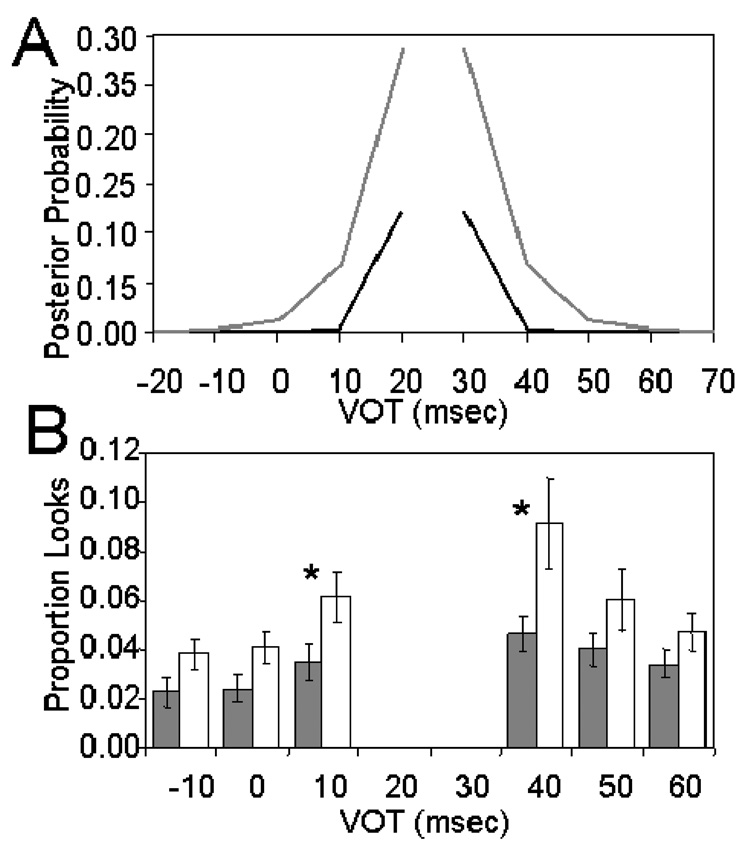
In the categorization task described above (but without the distributional manipulation), McMurray et al. (2002) found that looks to the competitor object (the beach when the listener chose the peach) increased with increasing distance from the category boundary. If the proportion of time listeners spend looking at each object reflects how strongly they are considering that object as a potential referent, then according to our model, proportion of looks should reflect the posterior probability of each object given a particular VOT value. Figure 4a shows the posterior probability of each category (calculated from (1) as before) for the less likely object (i.e., the competitor) for each VOT value given our distributions. Posterior probability increases for VOT values closer to the category boundary, similar to the increase in looks to the competitor object in McMurray et al. Importantly, our model makes two new predictions. The first is that the increase in posterior probability is not linear, but rather varies little around the category mean and then increases rapidly near the category boundary. The second is that the posterior probability is a function of the uncertainty in the distributions. For distributions with greater overlap (light lines), posterior probability increases more quickly than for distributions with less overlap (dark lines). If the proportion of looks to each object reflects the posterior probability, we expect to see different patterns for listeners who are categorizing stimuli from distributions with different variances.

Figure 4.

Relationship between posterior probability and looks to the competitor object for each VOT. [A] Posterior probabilities of the competitor words calculated using Equation 1 for the narrow (dark lines) and wide (light lines) distributions. [B] Proportion of looks to the competitor object for the narrow group (shaded bars) and wide group (open bars) for all VOT values with sufficient trials to analyze. Error bars indicate SEM. * p <.05.

Methods

Participants were 24 monolingual native English-speaking students from the University of Rochester with no known hearing problems (12 each in the wide and narrow conditions), Participants were tested individually in a quiet room. Sessions lasted approximately one hour. Participants were given the opportunity to take breaks and were paid $7.50.

Materials

Auditory stimuli were synthesized using the Klattworks¹ interface to the 1988 Klatt synthesizer (Klatt, 1980). VOT was manipulated in twelve 10 ms steps from −30 ms to 80 ms. Negative VOT values were created by adding voicing before the stop burst. Positive VOT values were created by replacing successive frames of voicing after the stop burst with aspiration. All other parameters were held constant across words and were modeled on natural stimuli. Three continua were created with endpoints corresponding to “beach”-“peach”, “beak”-“peak” and “bees”-“peas”. Each group of listeners heard 228 tokens, 76 from each of the 3 continua. The number of tokens of each step is shown in Table 1. Six filler items were also synthesized: “lake”, “rake”, “lace”, “race”, “lei” and “ray”.

Table 1.

Number of repetitions of each VOT value in the narrow and wide variance conditions.

VOT	−30	−20	−10	0	10	20	30	40	50	60	70	80
Narrow	0	3	27	54	27	3	3	27	54	27	3	0
Wide	3	12	27	30	27	15	15	27	30	27	12	3

Procedure

Participants were seated in front of a computer screen at a comfortable viewing distance and wore an SR Eyelink II head mounted eye-tracker with a sampling rate of 250Hz. Auditory stimuli were presented over Sennheiser HD 570 head phones at a comfortable listening level. The session began with 12 familiarization trials in which participants saw the pictures and their corresponding written labels once each. No auditory stimuli were presented during familiarization.

Each experimental trial began with a display containing four pictures, two test items and two filler items, one in each quadrant (Figure 2). One of the auditory stimuli was presented and participants chose the picture they thought most appropriate by clicking on it with the mouse. Eye movements were monitored from the onset of the auditory stimulus until participants made a response.

Figure 2.

Example display screen containing the items “beach”, “peach”, “lace” and “race”. Locations of items were randomized across trials. Actual displays were in color.

Each participant heard an equal number of test and filler items. For a particular display all alternatives were equally likely. Trials were randomly ordered. Filler items were included to provide some variety in the task and to make the design less obvious to the listeners.

Results

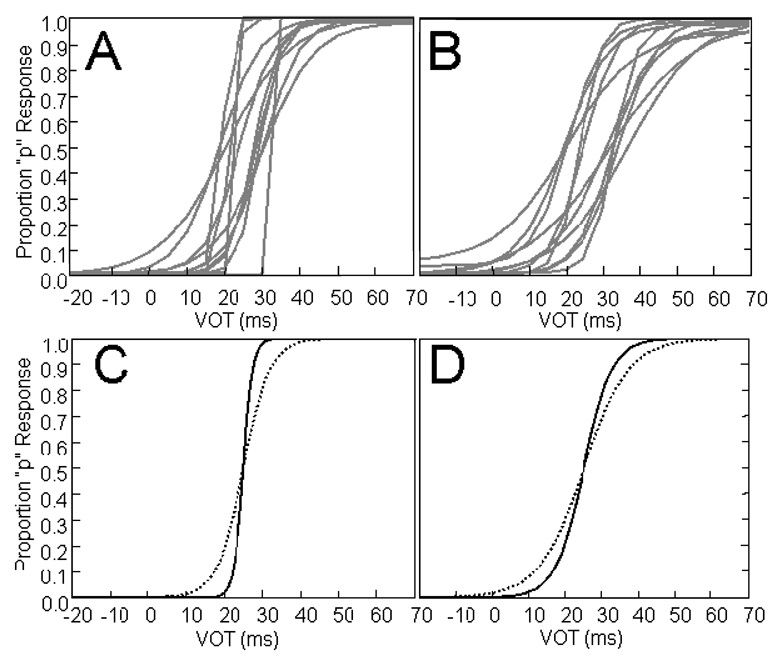
Categorization functions were fit for each participant in the two cue-variability conditions using a fitting algorithm designed for psychometric functions (Wichman & Hill, 2001a)². Participants were excluded and replaced if their fitted category boundaries were more than 15 ms different from the 25 ms boundary used in the distribution (two participants were replaced in the wide condition). Figures 3a and b show individual categorization functions for listeners in the narrow (mean RMSE = 0.07) and wide (mean RMSE = 0.05) conditions. As predicted, categorization functions in the wide condition had shallower slopes³ (mean = 6.2, sd = 0.89) than functions in the narrow condition (mean = 3.5, sd = 0.76). This difference was significant (t(22) = −2.4, p = 0.02). The slopes of the functions in each condition were compared to the optimal function given the distributions. Figure 3c shows the optimal function given the narrow distributions (solid line) and the empirically obtained function (dashed line) using the average slope of listeners in the narrow condition. Figure 3d shows the optimal function and empirically obtained function for the wide condition. As predicted, listeners are less certain than the optimal observer given either of the distributions.

Figure 3.

Fitted response curves for individual participants in [A] narrow condition and [B] wide condition. Optimal response curves (solid lines) and curves from average slope of individuals (dashed lines) for participants in [C] narrow condition and [D] wide condition.

While the source of this additional uncertainty is unknown, and may differ from listener to listener, it should not vary for the two conditions. We quantified the amount of additional uncertainty using the observation of Feldman and Griffiths (2007) that given the categorization function (2)

$$p(\mathit{\text{category}}A|\mathit{\text{stim}}X)=\frac{1}{1+e^{-g\mathit{\text{stim}}X+b}}$$ (2)

the slope (g) is given by (3). The equation in (3) assumes that both categories have the same variance $({\sigma }_{\mathit{\text{Category}}A,B}^2)$ and any additional uncertainty can be described as a Gaussian distribution with zero mean and some variance $({\sigma }_N^2).$

$$\mathit{\text{slope}}=\frac{{\mu }_{\mathit{\text{Category}}A}-{\mu }_{\mathit{\text{Category}}B}}{{\sigma }_{\mathit{\text{Category}}A,B}^2+{\sigma }_N^2}$$ (3)

Using (3), the ${\sigma }_N^2$ values for both groups (Narrow = 10.7, Wide = 10.8) were very similar, suggesting that the same additional source of uncertainty affected responses in both groups and was independent of the distributions themselves.

We also examined eye movements (Allopenna, Magunson & Tanenhaus, 1998). From the posterior probability functions in Figure 4a, we predicted that the largest difference in looks to the competitor object (i.e., “peach” for short VOTs and “beach” for long VOTs) between the two groups would be at 20 and 30 ms, a smaller difference at 10 and 40 ms, and no difference at other VOT values. Because there were so few trials at VOT values of −20, 20, 30 and 70 ms (see Table 1), we could not analyze eye-movements for these values. Figure 4b shows the proportion of looks for the remaining VOT values. A repeated measures analysis of variance (ANOVA) was performed separately for the “b” (−10, 0, 10) and “p” (40, 50, 60) sides of the continuum. On the “b” side there was a significant effect of VOT (F(2,44) = 9.09, p <.0001), a significant effect of condition (F(1,22) = 5.2, p<.05), and no interaction (F(2,44) = 1.08, p = 0.42). On the “p” side there was a significant effect of VOT (F(2,44) = 13.4, p <.0001), no effect of condition (F(1,22) = 3.5, p =.07), but a significant interaction (F(2,44) = 4.60, p < 0.05). As predicted, the largest effects were at 10 ms and 40 ms. Planned t-tests showed that the effect of group was significant both for 10 ms (t(22) = 2.10, p<.05) and for 40 ms (t(22) = −2.22, p<.05) but not for any other VOT values. The size of the effect was slightly larger on the “p” side of the continuum. Natural VOT values are more variable for the “p” than for the “b” category (Lisker & Abrahmson 1964) and a production study using the words from the present study found the same pattern. This asymmetry may have made listeners more sensitive to our manipulation for the “p” category.

Discussion

We evaluated an ideal observer model, which used the probability distribution of an acoustic-phonetic cue (VOT) to estimate the probability that a token was an example of a particular category (e.g., “peach”). Our results provide two kinds of evidence in support of this model. First, the average categorization slopes for the two conditions were well predicted by the distributions of the cues, given some additional source of uncertainty constant across both conditions. Second, participants’ uncertainty about their decision (as indexed by looks to the competitor object) also followed the pattern predicted by the distribution of cues.

Any ideal observer model makes specific assumptions about the task (goals) of the observer. We described the goal in terms of categories and the evidence in terms of probabilistic acoustic-phonetic cues, and we excluded all other sources of information. We assumed that the categories listeners were identifying were lexical items. However, our data are also consistent with feature level categories (e.g., voiced and voiceless), phoneme level categories (e.g. /b/ and /p/) or syllable level categories (e.g. /bi/ and /pi/). In this study it is not possible to know at which level listeners tracked these distributions or to what degree they would generalize to other examples (e.g., other voiced stops or words containing /bi/ and /pi/). It remains an important theoretical and empirical question to determine over which categories listeners calculate distributions.

Describing the evidence in terms of probabilistic cues is also important. It is a powerful characterization because any acoustic variable can be incorporated, so long as it is informative. Moreover, the informativeness of the cue is defined by its distribution for each category. In the extreme, a cue with completely overlapping distributions for each category would be uninformative. Thus we have a principled way to make a quantitative prediction about the contribution of any acoustic variable to word recognition.

Our model considered only the role of information available in the probability distributions of acoustic-phonetic cues. For the purposes of our categorization task, this may be all the information that is available. For speech perception in general, however, the signal is much richer and listeners may use other information in making their decisions. A more complete model would incorporate all available information, including information from the situational and linguistic contexts. Any of this information could affect the prior probability of a particular category, thereby creating a bias towards one category over another. Norris and McQueen (in press) present a Bayesian model of continuous speech that incorporates these assumptions and is consistent with our results from isolated words.

It is also important to note that many sources of variability (eg. from speaker or context) were excluded from this experiment. Important questions for future research will be how listeners cope with this additional variability, if they can make use of the context it occurs in and whether they will also behave optimally under the more variable circumstances found in natural language.

In summary, the close relationship between posterior probability and both response choice and probability of looks to an object suggests that these two measures reflect listener’s estimates of posterior probability. Furthermore, it suggests that listeners are acting in a manner consistent with the probability distributions they have heard when using acoustic information to recognize words.