Abstract
Microarray technology provides a powerful tool for the expression profile of thousands of genes simultaneously, which makes it possible to explore the molecular and metabolic etiology of the development of a complex disease under study. However, classical statistical methods and technologies fail to be applied to microarray data. Therefore, it is necessary and motivated to develop the powerful methods for large-scale statistical analyses. In this paper, we described a novel method, called Ranking Analysis of Microarray data (RAM). RAM, which is a large-scale two-sample t-test method, is based on comparisons between a set of ranked T-statistics and a set of ranked Z-values (a set of ranked estimated null scores) yielded by a “randomly splitting” approach instead of a “permutation” approach and two-simulation strategy for estimating the proportion of genes identified by chance, i.e., the false discovery rate (FDR). The results obtained from the simulated and observed microarray data shows that RAM is more efficient in identification of genes differentially expressed and estimation of FDR under the undesirable conditions such as a large fudge factor, small sample size, or mixture distribution of noises than Significance Analysis of Microarrays (SAM).
Keywords: Microarray, t-test, ranking analysis, false discovery rate
Introduction
Microarray technology provides a powerful tool for measuring the expression levels of large numbers of genes simultaneously, and creates unparalleled opportunities to study complex physiological or pathological processes, including the development of disease, that are mediated by the coordinated action of multiple genes [1]. Detection of genes differentially expressed across experimental, biological and/or clinical conditions is a major objective of microarray experiments. Methods for finding genes significantly differentially expressed in the context of microarray data analysis can be classified into three major groups [2,3]: marginal filters, wrappers [4], and embedded approaches [5,6]. The wrapper and embedded methods are a type of search algorithms by which candidate gene subsets that are useful to build a good predictor are constructed and selected and then evaluated by using a classification algorithm [3,7]. The filter approaches are a type of simple and fast-speed method including t-tests and nonparametric scoring [8,9] and analysis of variance (ANOVA) [1,10] for searching for the features (genes) or feature (gene) subsets that are irrelevant and independent of each other [3, 7]. For the microarray data, the filter approaches encounter a challenging simultaneous inference problem, as the probability of committing a type I error increases with the number of tests performed [11]. In order to resolve the statistical problem in testing a large family of null hypotheses, several multiple procedures have been developed. The Bonferroni procedure, the Holm procedure [12], Hochberg procedure [13], the Westfall and Young procedure [14] address the multiple test problem by controlling the family-wise error rate (FWER), which is the probability that at least one false positive occurs over the collective tests [15]. However, these methods are based on the assumption that different tests are independent of each other, they are, thus, not well suited to microarray data, often being too stringent and may yield no or few positive genes [16] and may result in unnecessary loss of power. Benjamini and Hochberg [17] have proposed an alternative measure, the false discovery rate (FDR), to control erroneous rejection of a number of true null hypotheses. FDR is an expected proportion of the false positives among all the positives detected. The FDR-based multiple testing approaches, such as the Benjamini and Hochberg(BH) procedure [17,18] and the Benjamini and Liu-procedure [19] have been developed for testing for a large family of hypotheses. These procedures are generally suited to larger sample sizes because small sample sizes lead FDR to be too “granular” [16]. Most recently, Storey [20] and Storey and Tibshirani [21] developed a new measure, i.e., positive FDR (pFDR) that is an arguably more appropriate variation. It multiplies the FDR by a factor of, which is the estimated proportion of non-differentially expressed genes to all genes on π0 the arrays [22]. The estimate of pFDR is smaller than the estimate of FDR [22]. Tsai et al. [23] suggested the use of the conditional FDR (cFDR) on the most significant findings. Pounds and Cheng [15, 24] proposed the spacing LOESS histogram (SPLOSH) approach to estimate of cFDR.. Tusher et al. [16] developed a new FDR-based method, called Significance Analysis of Microarrays (SAM). SAM is very popular because it can identify genes with significantly expressional change and can estimate FDR based on permutations. However, the conventional permutation approach is not the most appropriate method for estimating the null distribution for most microarray data because sample sizes in such experiments are commonly small which yield relatively small number of permutations and lead to inaccurate ranking of scores. Although SAM has the advantage of being distribution-free, its use of a fudge factor (S0) makes it mostly applicable to normal distributions because S0 is in general smaller than or equal to 1 in normal distributions. Non-normal distributions or small sample sizes can produce a larger S0, which often makes SAM loss its power or be not applicable.
These problems in SAM led us to develop a new statistical method called ranking analysis of microarray (RAM) data. The overall approach of RAM is somewhat similar to SAM, which is to identify genes with significant expression changes through the use of gene-specific t-tests, but RAM evaluates its significance based on an improved empirical distribution generated by a “randomly splitting” approach instead of the permutation approach and implementation of a simulation-based interval method for estimation of FDR. As a result, the RAM has all the major advantages of SAM, plus performs very well for small sample sizes, which are typical in microarray experiments.
Methods
T-statistic
For simplicity, we will focus our discussion on the analysis of expression data from experiments of two different classes (designated as 1 and 2), which is very common in practice. The two classes may correspond to two different genotypes of individuals, treatments, cell types, tissues, etc. Let N be the number of genes examined and mik be the number of replicate observations for the expression of gene k (k = 1, …, N) in class i (i =1, 2). We will refer to the collection of all the observations for a given gene in class i as sample i. Therefore, mik is the size of sample i for gene k. Typically m11 = m12 = … = m1N = m1 and m21 = m22 = … = m2N = m2, otherwise the experiments is said to have some missing observations
Let x̄ik and represent the mean and variance of the expression of gene k in sample i, respectively. Define for gene k
The traditional t-test statistic for testing if there is a significant difference between two sample means is equal to
where in the current context
for unequal variances for the two class experiments or
for equal variances. Although the traditional t-statistic is a reasonable choice for some expression data sets, its applicability is often questionable because that a small sampling variance (≪ 1), which can often arise due to randomness from large number of genes and small sample size, and relatively large value of dk may lead to erroneous conclusion. Such effect is generally known as the fudging effect. To reduce the fudging effect, Tusher et al. [16] proposed a modified t-statistic defined as
where S0 is a constant representing the minimal coefficient of variation of tk computed as a function of σk in the moving windows across the data. However, in our own studies, we noted the fudging effect using the modified t-statistic is still quite strong when the sample size is small. In particular, small sample size often leads to an unreasonably large value of S0 that dominates the test statistic and consequently reduces the power of the analysis. To circumvent the problem, we propose a simple alternative correction δk for the variance of expression for gene k as
| (1a) |
for the case of unequal variances and
| (1b) |
for the case of equal variances where
| (2) |
Thus, the t-statistic for the difference of expression levels of gene k is redefined as
| (3) |
Since Tk = tk unless dk > σk <1, the new test statistic is a simpler extension of the traditional t-statistic than that proposed by Tusher et al. [16].
Ranking Analysis
To identify genes whose expression levels are significantly different in two experimental conditions, a common practice is to rank the genes according to their values of the chosen statistics, which in our situation is T. Suppose Tk* is the k*-th largest T value, then its corresponding gene k is said to have significantly different expression between the two experimental conditions for a given threshold value Δif
| (4) |
where Zk* = E(Tk*) is the expectation of Tk*under the null hypothesis that there is no gene having a significant difference in expression. This type of test is known as the Ranking Test.
To enable the ranking test, it is critical to obtain a good estimate of Zk*. Tusher et al. [16] proposed a permutation approach for this purpose, which uses a standard permutation procedure for each gene. This process works well if the sample size is large. When the sample size is small, however, the number of permutated samples for each gene is rather small, which leads to a biased ranking test and even renders the test not applicable. This appears to be caused by the randomness introduced by permutations that lead to biased tail distributions for ranked values. The observations from analyzing both real and simulated data lead us to develop a Randomly Splitting (RS) approach to estimate Z as follows.
First each sample is randomly split into two subsamples with size difference not larger than a given value C. We found that it is best to set C=4. For the J-th split, let be the mean of subsample h of sample i for gene k. Define and , and hence,
| (5) |
The splitting process is carried out for every gene, and define
The set of values is then ranked. Let be the k*-th largest value for the J-th split. Then we estimate Zk*by the mean of over all the splits, i.e.
| (6) |
Fig. 1(panel A) shows the use of Zk* in the identification of the genes that are differentially expressed in a set of 3000 genes in a stroke response experiment. In this figure the solid line represents T = Z and the two dashed lines represent the lower and upper boundaries corresponding to a threshold Δ. The dots below the lower boundary and over the upper boundary represent genes that are significantly expressed at the given threshold Δ.
Fig. 1.
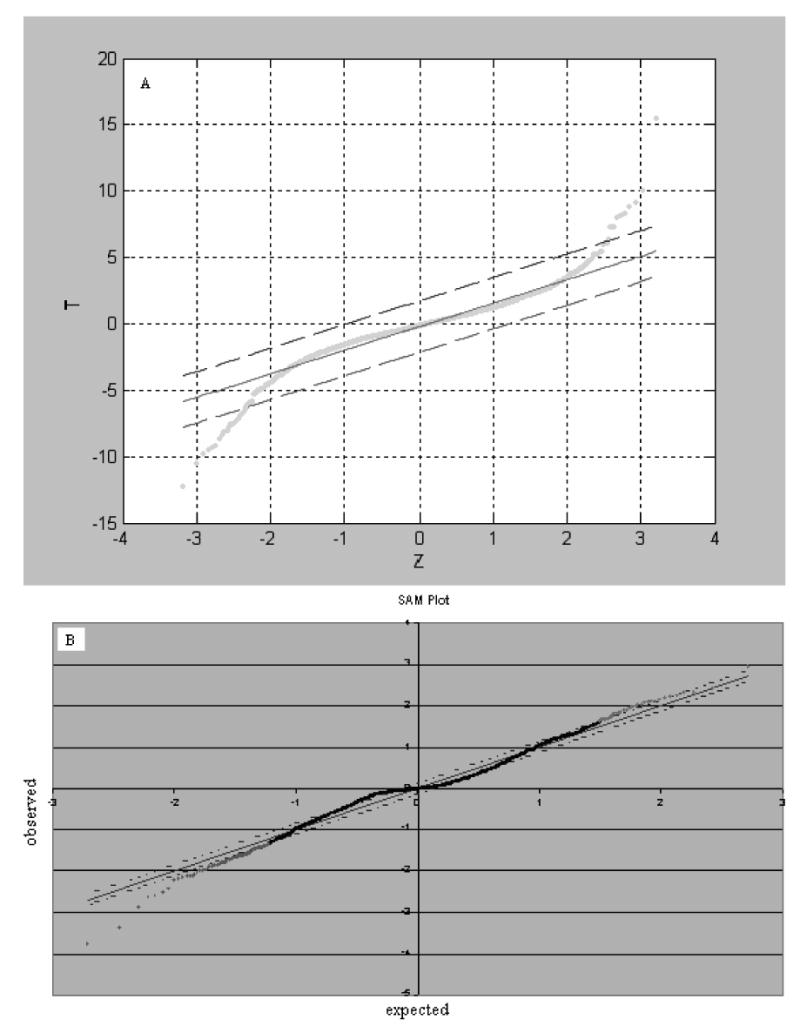
Identification of the genes significantly differentially expressed. Panel A is a plot of T-values vs Z-values based on the observed data of 3000 genes in two samples each consisting of 12 rat individuals in response to stroke where estimates of Z-values were obtained by use of the RS approach. Panel B is plot of observed T vs expected T (Z) in SAM. The simulated data set was comprised of 30% expression noises following gamma distribution and 70% following normal distribution where expression levels of 3000 genes in two samples each consisting of 12 replicates were simulated using one set of the observed sample means and two sets of the observed sample variances, and treatment effect values of G= 10R (for 30% of the genes) where R is a random uniform variable over (0, 1].
Estimate of FDR
Consider a series of threshold values Δi (i=1,…L). Let N(i) be the number of genes that are significant at the threshold Δi by the ranking analysis. N(i) is then comprised of two parts: the number of true positives Nt(i) and the number of false positives Nf(i). Therefore N(i) = Nt(i) + Nf(i). The false discovery rate (FDR) at the threshold Δi can be written as RFD(i) = Nf(i)/N(i) which requires to be estimated since Nf(i) is unknown. To improve the accuracy of estimating FDR, we propose a new strategy to obtain FDR as an average of two estimates each derived from simulation under a specific condition. The first estimate is carried out as follows.
For each gene, two samples of m replicates are simulated from a normal distribution, one with mean randomly set to be or and variance , another with mean randomly set to be or and variance , where is the mean of subsample h of the sample i for gene k produced by the RS procedure in the observed data.
The process will produce M sets of simulated data each is subjected to the ranking analysis described in the previous section. For each simulated data set, every ranked position has thus a corresponding T value that is denoted by . Since we are concerned about false positive, we consider only those genes that are not significant in the original ranking analysis. Comparing to Z̄k* for every ranking position will allow one to identify genes that are becoming significant. The number of such genes in the J-th set of simulation data at the threshold Δi is denoted by N(1, J,i).
Let which is the mean number of N(1,J,i). For an ascending series of threshold values, N(1,i) rises initially and declines when the threshold value exceeds a certain value Δ. Define
| (7) |
as the first estimate of FDR where and N(1,i) = N(Δ) when Δi< Δ. f(1,i) is thus a decreasing function and bounded between 1 and 0 (See Fig. 2).
Fig. 2.
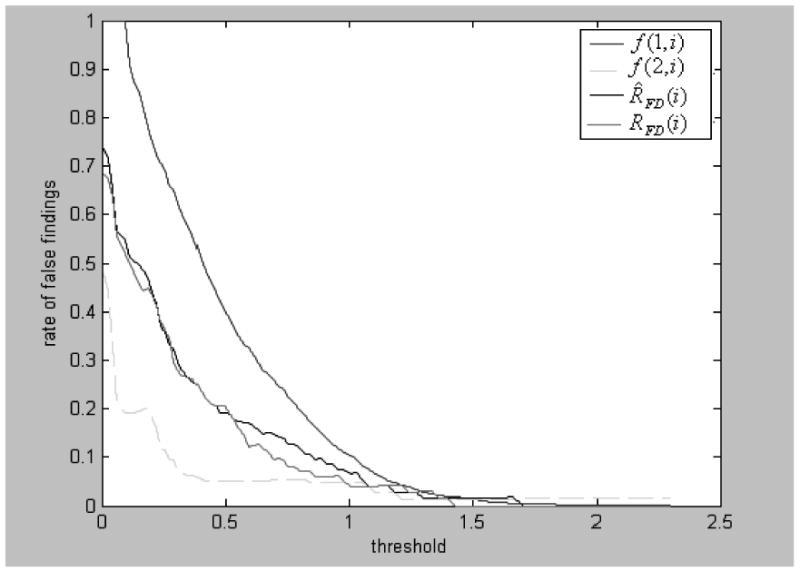
Estimation of the FDR. f (1,i) and f (2,i) are two threshold functions and are used to construct an estimation interval for estimate of FDR at threshold Δi. RFD (i) and R̂FD(i) are true and estimated FDR at threshold Δi, respectively, where RFD(i) were calculated by comparing genes identified by RAM with those given treatment effect (G = 10R).
The second estimate of FDR is obtained also from simulation. The simulation of the two samples for each gene is done in the same way as the first simulation, except that the two means are set to be equal, i.e., or . Also correspondingly for the J-th simulation data set, ranking analysis of the T values lead to , where “2” represents the second simulation. is compared to its average T̄k*2, and the significances across all the ranking positions at threshold Δi are counted as N(2,J,i). Let . Since the noise distribution produced by the RS approach from the simulated data agrees well with that produced by the RS approach from the observed data (see Fig. 3 panel B and Fig. 4 panels C and D), N(2,i) is a reasonable estimate of Nf(i) for a given threshold Δi. However, in order to avoid the possibility that R(FD,i) = N(2,i)/N (i) = ∞ occurs when N(i) =0, in particular, in the extreme cases of which there is no or small expression difference between two samples. We define
Fig. 3.
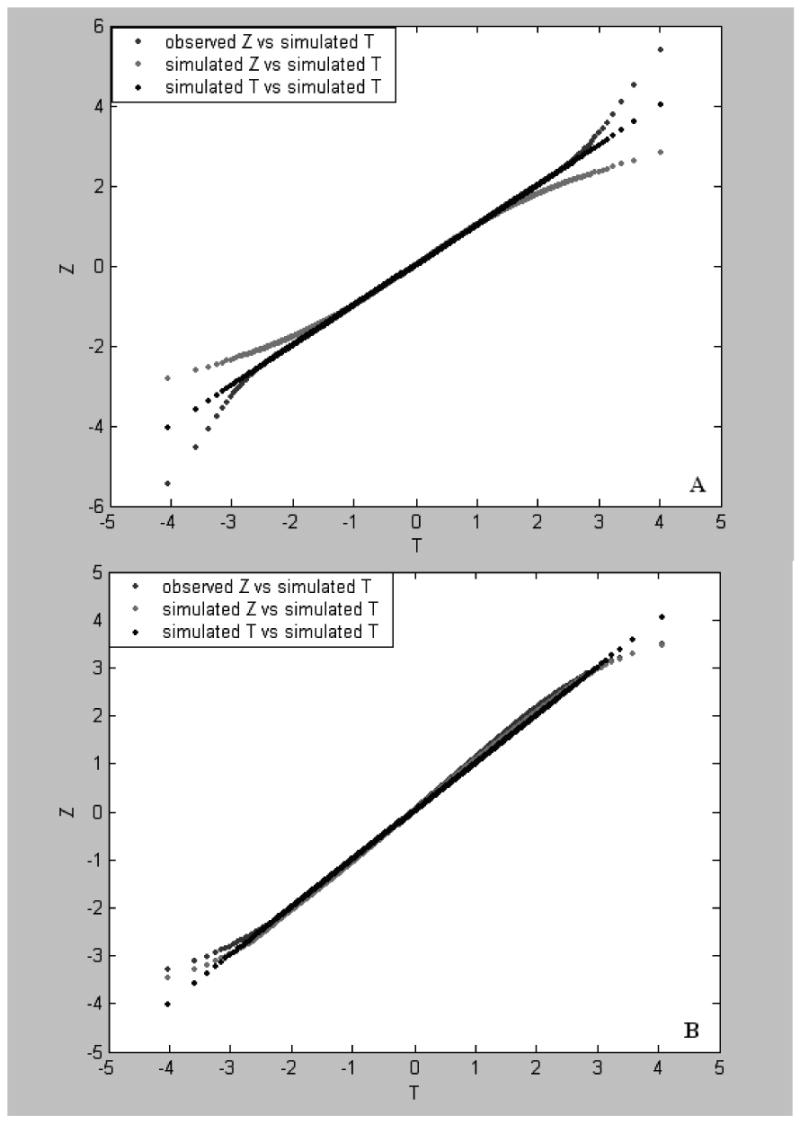
Plots of Z-values vs T-values. The observed Z-value (the b line) and simulated Z-value (the c line) were obtained by the permutation approach (panel A) and the RS approach (panel B). The observed microarray data of 3000 genes were obtained in two samples each consisting of 12 rat individuals. The first set of the simulated microarray data were produced using the pseudorandom generator and one set of 3000 observed means and two sets of 3000 observed variances where no gene was not given a treatment effect value. The simulated T- values (the a line) were a set of 3000 null scores produced from 100 repeated simulations of the first set of the simulated data (see text).
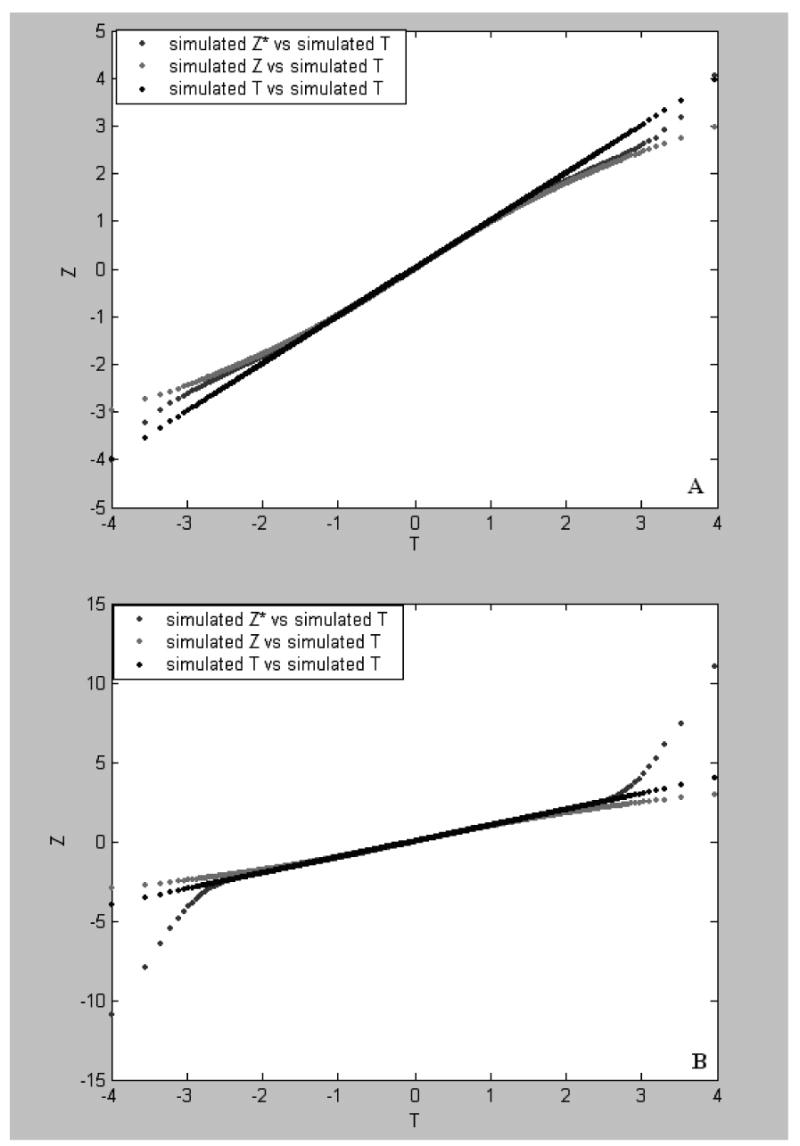
Fig. 4.
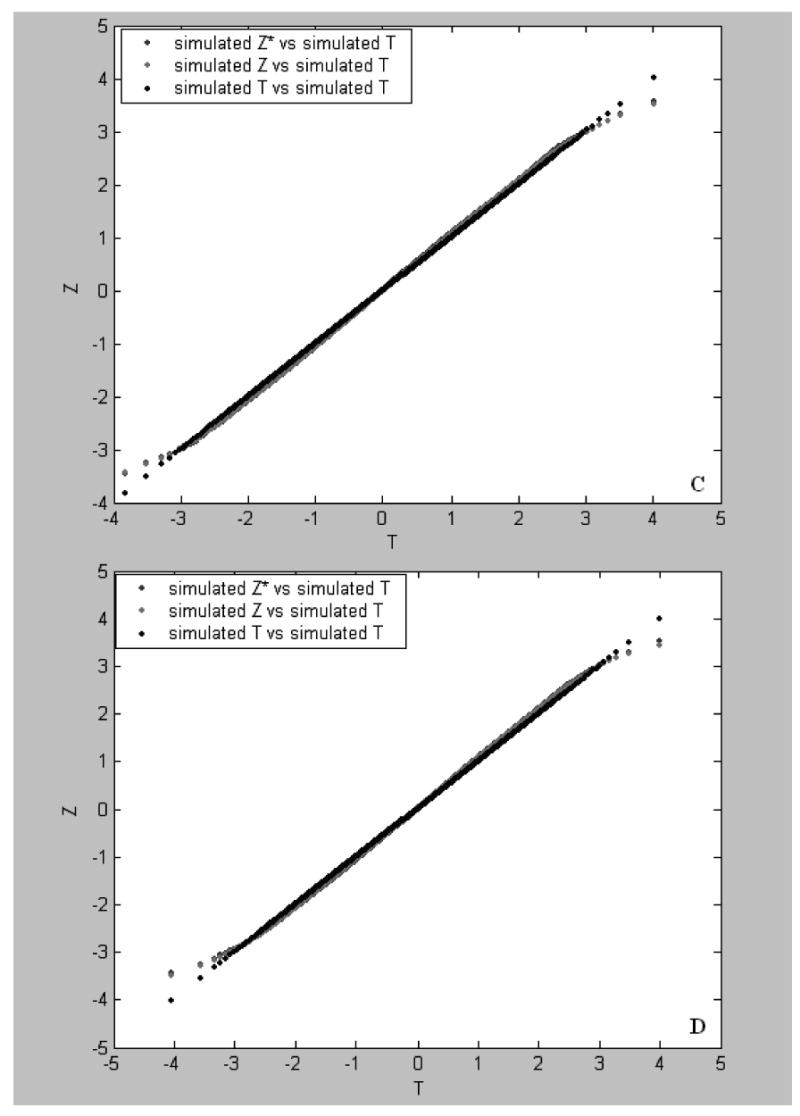
Plots of Z-values vs T values. The simulated Z-values were obtained from the first (the c line), second (the b lines in panels A and C) and third (the b lines in panels B and D) sets of the simulated data of 3000 genes, respectively. In the first, second, and third simulation sets, treatment effect values of G=0R, 10R and 30R were randomly assigned to 30% of the genes, respectively, where R is a random variate in the uniform distribution (>0,1] (see text for simulation). The simulated T-values (the a line) were a set of 3000 null scores (see text). The results shown in A and B were obtained by the permutation approach and those shown in panels C and D were based on the RS approach.
| (8) |
as the second estimate of FDR. Equation (8) shows that f(2,i) = 1 when N(i) = 0 and N(2,i) ≥ 1, f(2,i) = 0.5 when N(i) = N(2,i), f(2,i) < 0.5 when N(i) > N(2,i), and f(2,i) = 0 when N(i) ≥ 1 and N(2,i) = 0.
Although we intended to find a lower and upper bounds for FDR, it can be seen from Fig. 2 that although the two estimates of FDR provide two bounds for the FDR, f (1,i) does not remain as the lower bound nor the upper bound, same as f(2,i). The role of the two in bounding the FDR switches after certain threshold value. For this reason, we explore a single estimate of FDR which value lies between the two bounds. One conservative estimate is to give more weight to the larger of the two bounds, which results in the third estimate of FDR as
| (9) |
where ai = f(1,i)/[f(1,i) + f(2,i)] and bi = 1 − ai. We found that at threshold level Δi, a better estimate of FDR is obtained by
| (10) |
To further smooth the estimates of FDR, consider the difference between the numbers of genes found to be significant at adjacent thresholds Δi and Δi+1, define a recursive formula modifying the probability fi as
| (11) |
where pi = [N(i) − N(i + 1)]/[1 + N(i) − N(i + 1)]and qi = 1 − pi. Equation (11) suggests that fi+1 =fi if N(i) = N(i + 1). Thus, the number of the false discoveries among those found to be significant at threshold Δi in the observed data is estimated by
| (12) |
and an estimate of the FDR at threshold Δi is given by
| (13) |
It can be seen from Fig. 2 that the line for the true value RFD(i) agrees well with that for R̂FD(i), indicating that R̂FD(i) is a good estimate of FDR. We also found that, if no gene in the simulation was found to be significant, R̂FD(i) would be more than 0.5 at threshold Δi of f(1,i) < f(2,i) (the result is not shown).
Simulation Results
Estimate of The Null Distribution
To determine if the empirical distributions obtained by the permutation approach and the RS approach are appropriate for the analysis of expression data, we simulated three sets of microarray data sets each consisting of 3000 genes and two samples of 12 replicates each. The means and variances for each gene are set to the observed means and variances from the real microarray data obtained from our laboratory. In our real microarray data sets, the expression levels of 3000 genes were measured for two different strains [the spontaneously hypertensive rat (SHR) and stroke-prone spontaneously hypertensive rat (SHRSP)] each consisting of 12 rat individuals. In the first simulation data set, all 3000 genes were set to have no treatment effect. In the second and third simulation data sets, treatment effects of G=10R and G = 30R, respectively, were randomly assigned to 30% of the genes where R is a random variable in the uniform distribution (0,1].
In the ranking analysis, a set of Zk*values for each simulated data set was computed from 100 permutations or 100 random splits. As Zk*is an estimate of Tk*under the null hypothesis, a desirable property is that Zk*has a linear relationship with Tk*. This property can be seen by plotting Zk*versus Tk*. Fig. 3 shows the plot of Z obtained by the permutation (panel A) and RS (panel B) approaches. It can be seen from panel A that the Z-distribution obtained by either the permutation approach from the observed or the first simulated data sets remarkably deviates from the null distribution when |T| is large. More specifically, in the tails of T, the observed Z-values remarkably overestimate the null scores whereas the simulated Z-values underestimate the null scores. These patterns were also seen from simulation incorporating different treatment effects on gene-expressions. In Fig. 4 panel A, the Z*-values obtained by the permutation approach from the second simulation data set where 30% of the genes were given treatment effect values of 10R are in between the Z-values obtained by the permutation approach from the first simulation data set where no gene was given treatment effect and the null scores (simulated T-values) when T > 1.5 or < −1.5 whereas in Fig. 4 panel B, Z*-values from the third simulation data set where 30% of the genes were given treatment effect values of 30R are much larger than the null scores at T > 3 or much smaller than the null scores at T < −3. These results indicate that when the treatment effect contributing to expression variations of genes is weak or lacking, the Z-distribution yielded by the permutation approach would negatively deviate from the null distribution, i.e., Zk* ≤ Tk*> 0 or Zk*≥ Tk*< 0, so that type I errors observed in the ranking-test would be more than those expected. However, when a large treatment effect to different extent contribute to expression variations of a part of the genes, the Z-distribution would remarkably positively deviate from the null distribution, i.e., Zk* ≥ Tk*> 0 or Zk* ≤ Tk*< 0. In this case type II errors observed in the ranking-test would be much more than those expected. These observations in the case of small samples are in fact a general feature of the permutation approach (see Appendix A).
It can be seen from Fig. 3 panel B, however, that the Z-distributions obtained by the RS approach from the observed and the first simulated data sets and the simulated T distribution (the null distribution) are almost overlapped with each other. This is also shown in. Fig. 4 panels C and D where the Z*-values were obtained by the RS approach from the second and third simulation data sets and the Z- values from the first simulation data set. The similar results to those shown in Fig. 4 panels C and D were obtained in the case of sample size = 6. These results strongly suggest that the Z-distribution, as an empirical distribution, produced by the RS approach is a desirable approximation of the null distribution and in particular it is independent of treatment effect or sample size, which is essential for the rank-test.
Estimate of FDR
Since it is generally unknown if a given gene expresses differently in two different conditons, it is not necessarily best to use real data of gene expression to evaluate a FDR estimator. Therefore, we also conducted a computer simulation for comparing expression status (significance or insignificance) of a gene identified by a method with its real status. In this simulation study, we also generated two data sets of 3000 genes where treatment effect values of 10R were randomly assigned to 10% and 30 % of the genes, respectively, and sample size was set to be 6 replicates. This simulation procedure was iterated 20 times. Four criteria, i.e., absolute average, maximum and minimum, and variance of differences between the estimated and true numbers of the false discoveries across all R̂FD(i)% ≤ λ obtained from these 20 two-sample simulated data sets were used to assess an estimator. We set λ = 40, 30, 20, 10, and 5%. Table 1 summarizes the results obtained by applying RAM and SAM (the software comes from http://www-stat.stanford.edu/~tibs/SAM/) to these simulated data sets in the situations of 10% and 30% of the genes given effect values of 10R, respectively. These results shown in Table 1 clearly indicate that the RAM estimator has a much better accuracy in estimating FDR than the SAM estimator. In particular, for FDR of 5%, which is an important threshold value in practice, the RAM’s estimate is, on average, 0.65 false discoveries with variance <1, and variation interval of 1~3 false discoveries whereas SAM estimate is, on average, about 2 false discoveries with variance larger than 6 and variation interval of 7 false discoveries. Fig. 2 shows the whole profile of the RAM’s estimates of FDRs over all given thresholds based on the second simulation data set. In this profile, the estimated and true curves are well agreed, suggesting that the RAM’s estimate is reliable.
Table 1.
Difference between the estimated and true false discoveries at FDR [R̂FD]% ≤ λ obtained by SAM and RAM from the simulated microarray data of 3000 genes.
| Method | λ | Absolute Average | Variance | Maximum | Minimum |
|---|---|---|---|---|---|
| 30% of genes received treatment effect values of G =10R | |||||
|
| |||||
| RAM | 40 | 3.021 | 18.787 | 16 | −17 |
| 30 | 2.398 | 9.659 | 7 | −8 | |
| 20 | 2.119 | 7.677 | 6 | −8 | |
| 10 | 1.363 | 3.554 | 4 | −7 | |
| 5 | 0.649 | 0.739 | 2 | −1 | |
|
| |||||
| SAM | 40 | 5.309 | 55.240 | 11 | −25 |
| 30 | 3.406 | 18.915 | 11 | −9 | |
| 20 | 3.044 | 16.582 | 11 | −9 | |
| 10 | 2.209 | 9.214 | 6 | −4 | |
| 5 | 1.850 | 8.684 | 6 | −1 | |
|
| |||||
| 10% of genes received treatment effect values of G =10R | |||||
|
| |||||
| RAM | 40 | 1.961 | 7.219 | 8 | −5 |
| 30 | 1.471 | 3.963 | 6 | −3 | |
| 20 | 1.046 | 1.835 | 3 | −3 | |
| 10 | 0.641 | 0.763 | 2 | −2 | |
| 5 | 0.300 | 0.333 | 0 | −1 | |
|
| |||||
| SAM | 40 | 3.182 | 18.129 | 12 | −11 |
| 30 | 2.468 | 9.873 | 8 | −4 | |
| 20 | 2.048 | 7.268 | 7 | −3 | |
| 10 | 1.826 | 6.909 | 7 | 0 | |
| 5 | 1.667 | 6.705 | 7 | 0 | |
Identification of Differentially Expressed Genes
The exact distribution for the expression level of a gene is unknown in microarray experiments. For some genes, normal distributions may be appropriate, while for some gamma distribution may be more accurate, and for some none of the standard distributions may be adequate. When many thousands of genes are examined simultaneously, a variety of distributions is likely present. Therefore, it is appropriate to evaluate a method using data generated from a mixture of distributions. For simplicity, we limited ourselves in the simulation to use gamma and normal distributions to yield data sets consisting of 3000 genes in two samples each having 6 replicates. Then at random we mixed them together at a given proportion (for example, 30% gamma distribution and 70% normal distribution) to construct a new set of microarray data. We applied SAM and RAM to the simulation data set. The results are summarized in Fig. 1 panel B and Table 2 where the exchangeability (fudging) factor S0 = 10.75 at percentile= 33%. One can find in Fig. 1 panel B that all dots on plots are close to the expected lines, suggesting that the SAM fails to work in such data whereas the other result in Table 2 shows that RAM works very well for identifying genes that are significantly differentially expressed and for the estimation of FDR.
Table 2.
The results obtained by SAM and RAM from the simulated microarray data sets of 3000 genes where 30% of the genes were given treatment effect values of 8R and 30% of the expression noises followed a gamma distribution and the others followed a normal distribution.
| SAM
|
RAM
|
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Δi | N(i) | N̂f(i) | R̂FD(i) % | Δi | N(i) | N̂f(i) | Nf(i) | R̂FD(i) % | RFD (i) % |
| 0.00050 | 1127 | 1160 | 102.9 | 0.0676 | 1821 | 1296 | 1279 | 71.2 | 70.2 |
| 0.01035 | 351 | 292.5 | 83.3 | 0.0851 | 1715 | 1199 | 1199 | 69.9 | 69.9 |
| 0.01217 | 350 | 286 | 81.7 | 0.1025 | 1660 | 1147 | 1157 | 69.1 | 69.7 |
| 0.01943 | 346 | 282 | 81.5 | 0.1374 | 1505 | 753 | 1040 | 50.0 | 69.1 |
| 0.02073 | 345 | 277 | 80.2 | 0.1724 | 1372 | 462 | 938 | 33.7 | 68.4 |
| 0.02932 | 315 | 248 | 78.7 | 0.1900 | 1288 | 369 | 875 | 28.6 | 67.9 |
| 0.03368 | 311 | 239.5 | 77.0 | 0.2251 | 1137 | 295 | 764 | 25.9 | 67.2 |
| 0.04193 | 308 | 230 | 74.6 | 0.2428 | 984 | 232 | 657 | 23.6 | 66.8 |
| 0.05636 | 301 | 218.5 | 72.5 | 0.2782 | 802 | 172 | 523 | 21.4 | 65.2 |
| 0.06288 | 289 | 206.5 | 71.4 | 0.3138 | 401 | 82 | 230 | 20.4 | 57.4 |
| 0.06851 | 256 | 178 | 69.5 | 0.3677 | 102 | 21 | 21 | 20.6 | 20.6 |
| 0.08908 | 153 | 99 | 64.7 | 0.3858 | 99 | 20 | 20 | 20.2 | 20.2 |
| 0.11274 | 135 | 83 | 61.4 | 0.4039 | 97 | 19 | 19 | 19.6 | 19.6 |
| 0.12576 | 127 | 75.5 | 59.4 | 0.4405 | 95 | 18 | 18 | 18.9 | 18.9 |
| 0.13374 | 124 | 73 | 58.8 | 0.4589 | 92 | 17 | 17 | 18.5 | 18.5 |
| 0.14284 | 123 | 70 | 56.9 | 0.4775 | 89 | 16 | 16 | 18.0 | 18.0 |
| 0.14912 | 120 | 68 | 56.6 | 0.4961 | 87 | 15 | 15 | 17.2 | 17.2 |
| 0.15884 | 88 | 45.5 | 51.7 | 0.5337 | 83 | 14 | 15 | 16.9 | 18.1 |
| 0.16771 | 86 | 43 | 50.0 | 0.5909 | 79 | 12 | 13 | 15.2 | 16.5 |
| 0.18042 | 85 | 42 | 49.4 | 0.6103 | 77 | 11 | 13 | 14.3 | 16.9 |
| 0.18894 | 80 | 38 | 47.5 | 0.6494 | 74 | 10 | 11 | 13.5 | 14.9 |
| 0.19440 | 74 | 35 | 47.2 | 0.6692 | 72 | 10 | 10 | 13.9 | 13.9 |
| 0.19750 | 73 | 35 | 47.9 | 0.6892 | 71 | 9 | 9 | 12.7 | 12.7 |
| 0.20497 | 71 | 33 | 46.4 | 0.7502 | 68 | 8 | 9 | 11.8 | 13.2 |
| 0.20650 | 48 | 22 | 45.8 | 0.7918 | 65 | 6 | 8 | 9.2 | 12.3 |
| 0.21360 | 44 | 20 | 45.4 | 0.8344 | 64 | 6 | 7 | 9.4 | 10.9 |
| 0.21474 | 39 | 18 | 46.1 | 0.8560 | 61 | 6 | 5 | 9.8 | 8.2 |
| 0.21516 | 38 | 17 | 44.7 | 0.8779 | 60 | 5 | 5 | 8.3 | 8.3 |
| 0.21815 | 26 | 11 | 42.3 | 0.9226 | 57 | 5 | 4 | 8.8 | 7.0 |
| 0.22433 | 19 | 7 | 36.8 | 1.0156 | 47 | 3 | 4 | 6.4 | 8.5 |
| 0.23141 | 19 | 7 | 36.8 | 1.0893 | 42 | 3 | 2 | 7.1 | 4.8 |
| 0.23953 | 15 | 6 | 40.0 | 1.1147 | 41 | 3 | 2 | 7.3 | 4.9 |
| 0.27464 | 14 | 4 | 28.5 | 1.1939 | 40 | 2 | 2 | 5.0 | 5.0 |
| 0.45645 | 5 | 1 | 20.0 | 1.3691 | 36 | 2 | 2 | 5.6 | 5.6 |
| 1.02531 | 1 | 1 | 100.0 | 1.4011 | 34 | 2 | 1 | 5.9 | 2.9 |
| 1.04895 | 0 | 1 | NA | 1.4340 | 32 | 1 | 1 | 3.1 | 3.1 |
| 2.2410 | 24 | 0 | 0 | 0 | 0 | ||||
Note: Nf (,i) and RFD(i) are true number and the rate of false discoveries according to the comparison between identified and true gene differentially expressed in the simulated data
Application to the Real Microarray Data
Both SAM and RAM were applied to the two-sample real microarray data of 7129 genes obtained from two small samples (4 replicates for each sample) provided in the SAM software package. The results shown in Table 3 is helpful for explaining the observation in Table 1 of Tusher et al.[16]. A larger S0 (S0=3.3) is the primary cause for SAM’s poor performance: 12% FDR in the 48 genes identified to be significant at threshold Δ =1.2. It can be seen from Table 3 that RAM found 61 genes having significant expressional change at an acceptable FDR level of 3.3% whereas SAM identified only 21 genes at an acceptable FDR level of 4.7%. The difference of 40 genes between both is because of an unnecessarily larger fudging factor (S0= 3.4) used in SAM. In deed, these 40 genes all have d > σ < 1, suggesting that a large value of S0 indeed led some truly differentially expressed genes to be missed by SAM.
Table 3.
Numbers of genes called significant, and of the false discoveries estimated by SAM and RAM from the observed microarray data sets of 7129 genes in 4 replicate experiments provided in SAM software.
| SAM (S0= 3.46 at percentile = 0.01)
|
RAM
|
||||||
|---|---|---|---|---|---|---|---|
| Δi | N(i) | N̂f(i) | R̂FD(i) % | Δi | N(i) | N̂f(i) | R̂FD(i) % |
| 0.00676 | 4046 | 3736.4 | 92.3 | 0.04641 | 6834 | 5060 | 74.0 |
| 0.02311 | 4011 | 3682.4 | 91.8 | 0.10520 | 6392 | 4261 | 66.7 |
| 0.03355 | 3952 | 3621.4 | 91.6 | 0.16402 | 5956 | 3964 | 66.6 |
| 0.04874 | 3933 | 3591.4 | 91.3 | 0.22289 | 5539 | 1993 | 36.0 |
| 0.07252 | 3893 | 3551.5 | 91.2 | 0.28185 | 5144 | 1656 | 32.2 |
| 0.08402 | 3882 | 3536.5 | 91.1 | 0.34092 | 4736 | 1389 | 29.3 |
| 0.08731 | 3855 | 3499.5 | 90.7 | 0.40013 | 4188 | 1430 | 34.1 |
| 0.08885 | 3305 | 2955.7 | 89.4 | 0.45952 | 3752 | 1043 | 27.8 |
| 0.08977 | 3211 | 2879.7 | 89.6 | 0.51911 | 3245 | 553 | 17.0 |
| 0.09132 | 1936 | 1716.2 | 88.6 | 0.57893 | 2660 | 617 | 23.2 |
| 0.09278 | 1751 | 1529.3 | 87.3 | 0.63901 | 1795 | 100 | 5.6 |
| 0.09538 | 1739 | 1510.3 | 86.8 | 0.69939 | 1480 | 110 | 7.4 |
| 0.09691 | 1718 | 1487.3 | 86.5 | 0.76010 | 1220 | 71 | 5.8 |
| 0.09886 | 1703 | 1464.3 | 85.9 | 0.82118 | 783 | 61 | 7.8 |
| 0.10159 | 752 | 568.2 | 75.5 | 0.88266 | 310 | 17 | 5.5 |
| 0.10943 | 739 | 550.2 | 74.4 | 0.94457 | 6161 | 2 | 3.3 |
| 0.11610 | 599 | 436.8 | 72.9 | 1.00697 | 58 | 2 | 3.4 |
| 0.12068 | 531 | 383.3 | 72.1 | 1.06988 | 57 | 1 | 1.8 |
| 0.13922 | 410 | 268.3 | 65.4 | 1.13336 | 57 | 1 | 1.8 |
| 0.15164 | 352 | 218.4 | 62.0 | ||||
| 0.18234 | 268 | 155.9 | 58.1 | ||||
| 0.19807 | 261 | 147.9 | 56.6 | ||||
| 0.20716 | 213 | 116.9 | 54.9 | ||||
| 0.33398 | 167 | 64.9 | 38.9 | ||||
| 0.43301 | 124 | 39.9 | 32.2 | ||||
| 0.57814 | 88 | 19.4 | 22.1 | ||||
| 0.65578 | 74 | 12.9 | 17.5 | ||||
| 0.76837 | 62 | 9.9 | 16.1 | ||||
| 0.86358 | 46 | 5.9 | 13.0 | ||||
| 1.24876 | 36 | 2.9 | 8.3 | ||||
| 1.38245 | 26 | 1.9 | 7.6 | ||||
| 1.60219 | 21 | 0.9 | 4.7 | ||||
| 2.03175 | 12 | 0.9 | 8.3 | ||||
| 2.43241 | 11 | 0.9 | 9.0 | ||||
| 2.69035 | 3 | 0.9 | 33.3 | ||||
| 4.19555 | 0 | 0.9 | NA | ||||
Discussion
In conventional statistical resampling, permutation is a popular approach to estimate a null distribution. However, as seen from our analysis and as indicted in Appendix A, the distribution-free method based on permutations would be generally biased because for microarray data analysis small sample sizes limit the number of distinct permutation samples and ranking the T-statistics at each permutation does not completely remove the treatment effect contributing to gene-expression variations. The RS approach is developed in this paper to circumvent the aforementioned problems of SAM. The resulting RAM has the advantage of being insensitive to the treatment effect often present in real data and having a better estimate of FDR. Another important advantage of RAM is that it works well for small sample size that is particularly useful for analyzing microarray data that often have small sample sizes. In addition, the RS approach can be easily extended to the pair data set (see Appendix B)
FDR is often used to control error rate in the BH-procedure [18] and in SAM [16] and [22]. In practice, for a multiple-test method based on t-statistic, it is important to obtain an accurate estimate of FDR. In SAM, the FDR estimate is realized through the permutation approach in which fluctuations around expectation occur among permutated samples. The fluctuations would be impacted on by the data itself, i.e., sample size, treatment effect, and data noise. The RAM estimator of FDR is based on a two-simulation strategy so that it avoids these impacts on the estimate of FDR. Our simulation results indicate that the RAM estimator of FDR is generally accurate at a given threshold of interest.
In an idealized setting where all expression level is normally distribution, SAM and RAM all work well for identifying differentially expressed genes. However, in the case that most of the expression levels follow a normal distribution and a small fraction, for example, 30 percent of the genes, possibly follow a gamma distribution, SAM performs poorly or even fails to work due to a larger fudge factor S0 whereas RAM continues to performs well. In addition, small sample size makes it possible to produce the sample variances far smaller than 1 in a large-scale gene-expression profile. This situation, as seen in Tusher et al. [16], also produces a larger fudging factor for SAM, but in RAM this fudging impact can effectively be excluded.
Supplementary Material
Acknowledgments
This research has supported by grants from the U.S. National Institutes of Health R01 NS41466 (MF) and R01 HL69126 (MF), R01 GM50428 (YF) and funds from Yunnan University. We thank the High Performance Computer Center of Yunan University for computational support and Sara Barton for editorial assistance
Appendix A
Suppose we have two classes Xk = {xk1,…, xkm) and Yk = {yk1,…, ykn) of m replicates for gene k. A permutation produces two resampling classes Xk′ = {xk1,…,xkm−r, yk1,…,ykr) and Yk′ = {xk1,…,xkr, yk1,…,ykn−r). From these resampling two-class data, we have two resampling means
| (A1a) |
| (A1b) |
Let xkj = μk + τxk + exkj and ykj = μk + τyk + eykj where μk is overall mean (expectation) for expression levels of gene k, τxk and τyk are assumed to be treatment effects contributing to expression variation of gene k, exkj and eykj are expression noises. Thus, these two means can also be expressed as
| (A2a) |
| (A2b) |
where r is number of exchanged members between two classes. It is clear that with difference between and treatment effect difference is
if r = m/2, otherwise, d(τk) ≠ 0. In addition, rank of Z-values across all position at each permutation changes the Z-values in position k* in the rank space so that the component dealing with d(τk) in the Z-value in position k* in the rank space, that is, where or is a pooled standard deviation of two samples in position k* at permutation J. This indicates that the Z-distribution obtained by the permutation approach contains treatment effect difference for the microaaray experiments if r ≠ m/2. This is why a large treatment effect on expression levels of a part of the genes leads to an obviously “positive deviation” of the Z-distribution obtained by the permutation approach from the null distribution as seen in Fig. 3 panel A, Fig. 4panel A and B, say, Zk* ≥ Tk* ≥ 0 or Zk* ≤ Tk* ≤ 0 where Tk* = d(ek*)/σk* is a null score of the T-statistic.
For no treatment effect, i.e., τxk = τyk = 0 and for small sample size for gene k, ∑ek ≥ 0 or ∑ek ≤ 0, and hence, Equations A1a and A1b are changed to
| (A3a) |
| (A3b) |
In the difference between and , there is a error difference,
| (A4) |
where d(ek) = exk − eyk and d[ek (r)] = ēyk(r) − ēxk(r). It is clear from equation (A4) that d(εk) ≠ d(ek) if d[ek (r)] ≠ 0. On the other hand, due to ēxk(r) ∊ ēxk and ēyk(r) ∊ ēyk, d[ek (r)] = ēyk(r) − ēxk(r) is negatively related to d(ek) = ēxk − ēyk, that is, if d(ek) > 0, then d[ek (r)] ≤ 0 or if d(ek)] < 0, then d[ek (r)] ≥ 0. Again, rank of the Z-value across all positions leads to or consequently, the average of in position k* over all permutations is larger or less than or equal to zero, that is, or , which then results in a “negative deviation” of the Z-distribution from the null distribution as seen in Figures 3A, 4A and 4B, i.e., Zk* ≥ Tk* ≤ 0 or Zk*≤ Tk* ≥ 0.
Appendix B
For paired data, since two samples of mk observed values (x1k,…, xmkk) and (y1k,…, ymkk) become a sample of mk distant values (d1k,…, dmk k), k =1,…, N, the sample of mk replicates for distances can be also at random cut into two subsamples. Let dik = xik − yik = dk + exik − eyik = dk + eik, i = 1,…, mk where dk is difference between treatment effects on the expression of gene k. We then have . In two subsamples at split J, two subsample means are expressed as and where is average of errors in subsample i at split J for gene k in system g (g = x, y). Therefore, ēk is estimated by
say, ēk in the paired data is equivalent to that in the unpaired data. The null score of the T-statistic is estimated by the Z-value:
where σ 2 (dk) is the sample variance of distances between two paired data for gene k.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Kerr MK, Martin M, Churchill GA. Analysis of variance for gene expression microarray data. J Comput Biol. 2000;7:819–839. doi: 10.1089/10665270050514954. [DOI] [PubMed] [Google Scholar]
- 2.Li L, Jiang JW, Li X, Moser KL, Guo Z, Du L, Wang Q, Topol EJ, Wang Q, Rao S. A robust hybrid between genetic algorithm and support vector machine for extracting an optimal feature gene subset. Genomics. 2005;85:16–23. doi: 10.1016/j.ygeno.2004.09.007. [DOI] [PubMed] [Google Scholar]
- 3.Guyon I, Elisseeff A. An introduction to variable and feature selection. J Mach Learn Res. 2003;4(4):1157–1182. [Google Scholar]
- 4.Xing EP, Jordan MI, Karp RM. Feature selection for high-dimensional genomic microarray data. Machine Learning: Proceedings of the Eighteenth International Conference; San Francisco, Morgan Kaufmann, San Mateo, CA. [2001]. [Google Scholar]
- 5.Kohavi R, John GH. Wrappers for feature subset selection. Artif Intell. 1997;97:273–324. [Google Scholar]
- 6.Tsamardinos I, Aliferis CF. Ninth International Workshop on Artificial Intelligence and Statistics. Key West, FL: 2003. Towards principled feature selection: relevance, filters and wrappers. [Google Scholar]
- 7.Wolf L, Shashua A, Geman D. Feature selection for unsupervised and supervised inference: The emergence of sparsity in a weight-based approach. J Mach Learn Res. 2005;6(11):1855–1887. [Google Scholar]
- 8.Park PJ, Pagano M, Bonetti M. A nonparametric scoring algorithm for identifying informative genes from microarray data. Pac Symp Biocomput. 2001:52–63. doi: 10.1142/9789814447362_0006. [DOI] [PubMed] [Google Scholar]
- 9.Li L, Li X, Guo Z. Efficiency of two filters for feature gene selection. Life Sci Res. 2003;7:372–396. (Chinese) [Google Scholar]
- 10.Cui X, Hwang JTG, Qiu J, Blades NJ, Churchill GA. Improved statistical tests for differential gene expression by shrinking variance components. Biostatistics. 2005;6(1):59–75. doi: 10.1093/biostatistics/kxh018. [DOI] [PubMed] [Google Scholar]
- 11.Pan W, Lin J, Le CT. How many replicates of arrays are required to detect gene expression changes in microarray experiments? A mixture model approach. Genome Biol. 2002;3(5):Research0022. doi: 10.1186/gb-2002-3-5-research0022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Holm S. A simple sequentially rejective multiple test procedure. Scand J Stat. 1979;6:54–70. [Google Scholar]
- 13.Hochberg Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika. 1988;75:800–803. [Google Scholar]
- 14.Westfall P, Young S. Resampling-Based Multiple Testing. Wiley; New York: 1993. [Google Scholar]
- 15.Turkheimer FE, Smith CB, Schmidt K. Estimation of the number of “true” null hypotheses in multivariate analysis of neuroimaging data. Neuroimage. 2001;3:920–930. doi: 10.1006/nimg.2001.0764. [DOI] [PubMed] [Google Scholar]
- 16.Tusher VG, Tibshirani R, Chu G. Significance analysis of microarrays applied to the ionizing radiation response. Proc Natl Acad Sci USA. 2001;98:5116–5121. doi: 10.1073/pnas.091062498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. JR Stat Soc Ser B. 1995;57:289–300. [Google Scholar]
- 18.Benjamini Y, Drai D, Elmer G, Kafkfi N, Golani I. Controlling the false discovery rate in behavior genetics research. Behav Brain Res. 2001;125:279–284. doi: 10.1016/s0166-4328(01)00297-2. [DOI] [PubMed] [Google Scholar]
- 19.Benjamini Y, Liu W. A step-down multiple hypotheses testing procedure that controls the false discovery rate under independence. J Stat Plan Inference. 1999;82:163–170. [Google Scholar]
- 20.Storey JD. A direct approach to false discovery rates. JR Stat Soc Ser B. 2002;64:479–498. [Google Scholar]
- 21.Storey JD, Tibshirani R. Statistical significance for genome wide studies. Proc Natl Acad Sci USA. 2003;100:9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cui X, Churchill GA. Statistical tests for differential expression in cDNA microarray experiments. Genome Biol. 2003;4:210–219. doi: 10.1186/gb-2003-4-4-210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tsai C-A, Hsueh H-M, Chen JJ. Estimation of false discovery rates in multiple testing: application to gene microarray data. Biometrics. 2003;59:1071–1081. doi: 10.1111/j.0006-341x.2003.00123.x. [DOI] [PubMed] [Google Scholar]
- 24.Pounds S, Cheng C. Improving false discovery rate estimation. Bioinformatics. 2004;20:1737–1745. doi: 10.1093/bioinformatics/bth160. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


