Comment on: the Stokes–Einstein equation and the physiological effects of vitreous surgery

Editor,

We read with interest the recent editorial on the physiological effects of vitreous surgery, which highlighted the importance of the viscosity of the vitreous fluid on the rate of diffusion of small molecules of physiological importance (Stefansson & Loftsson 2006). From the Stokes–Einstein equation and previous measurements of the viscosity of the human vitreous body (Lee et al. 1992), it was suggested that the rate of diffusion should be 300–2000 times slower before vitrectomy than after. We agree that the rate at which small molecules are distributed in the eye is an important aspect of ocular physiology. However, the published measures of the viscosity of the vitreous were obtained from vitreous gel, while the Stokes–Einstein equation describes the effect of the viscosity on the rate of diffusion in a liquid.

David Maurice measured the rate of loss of radioactive protein from the centre of the vitreous body of living rabbit eyes. Using these measures and physical modelling, he concluded that the rate of diffusion of molecules in the intact vitreous body was experimentally indistinguishable from water (Maurice 1959). Dr Maurice’s measurements have since been used to model the distribution of many kinds of molecules in the eye.

To make more direct observations of diffusion in the vitreous body at the microscopic scale, we used fluorescence correlation spectroscopy (FCS) (Elson 2004). FCS measures the time spent by single fluorescent molecules in a tiny volume at the focal point of a laser beam. When their molecular weight is known, FCS provides a measure of the viscosity of the medium in which the molecules are moving. We collected data from the diffusion of two fluorescent molecules of different molecular weight, Alexa 488 (~ 0.5 kDa) and recombinant green fluorescent protein [GFP (~ 29 kDa)], in physiological salt solutions, homogenized porcine vitreous or intact porcine vitreous gel. Correlation spectra were collected using a Zeiss Confocor^™ (Thornwood, NY, USA) attachment on a LSM510 confocal microscope (Zeiss Confocor^™) at a point 100 μm into the solution or gel. The correlation spectra obtained are shown in Fig. 1; mean diffusion times and calculated diffusion coefficients for Alexa 488 and GFP are shown in Tables 1 and 2, respectively.

Fig. 1.

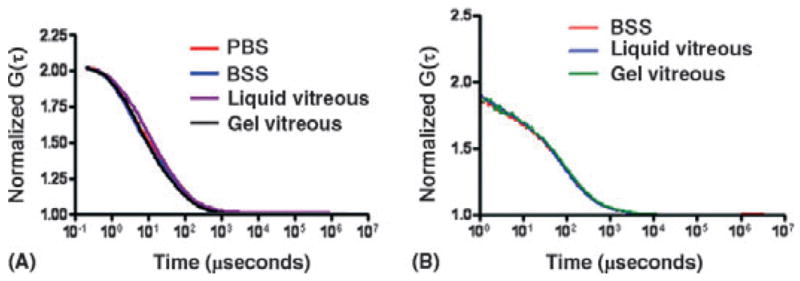
Correlation spectra for Alexa 488 (A) and recombinant green fluorescent protein [GFP (B)] in different media. BSS, balanced salt production; PBS, phosphate-buffered saline.

Table 1.

Mean diffusion times and calculated diffusion coefficients for Alexa 488.

Sample	Diffusion time (μseconds)	Diffusion coefficient (m2/second)
Alexa 488 in PBS	32.5 ± 0.2	3.0 × 10−10
Alexa 488 in BSS	30.9 ± 0.1	3.1 × 10−10
Alexa 488 in liquid vitreous	29.4 ± 0.3	3.3 × 10−10
Alexa 488 in gel vitreous	31.0 ± 1.0	3.1 × 10−10

BSS, balanced salt solution; PBS, phosphate–buffered saline.

Table 2.

Mean diffusion times and calculated diffusion coefficients for recombinant green fluorescent protein (GFP).

Sample	Diffusion time (μseconds)	Diffusion coefficient (m2/second)
GFP in BSS	79.5 ± 0.7	1.3 × 10−10 ± 1.2 × 10−12
GFP in liquid vitreous	71.9 ± 0.5	1.4 × 10−10 ± 1.1 × 10−12
GFP in gel vitreous	84.0 ± 1.1	1.2 × 10−10 ± 1.6 × 10−12

BSS, balanced salt solution.

As expected from its greater molecular weight, GFP had a longer diffusion time and lower diffusion coefficient than Alexa 488 under all conditions. However, the diffusion times and calculated diffusion coefficients of each fluorescent molecule measured in saline solutions, homogenized vitreous or vitreous gel were similar. According to the Stokes–Einstein equation, if the microscopic viscosity of the vitreous fluid or the vitreous gel were greater than saline, the calculated diffusion coefficients in the vitreous fluids would have been proportionally smaller in vitreous (gel or liquid) than in saline. Since these values were similar, the microscopic viscosity of liquid or gel vitreous is similar to saline. These measurements and the work of Dr Maurice suggest that the rate of diffusion of a molecule in the vitreous chamber is expected to be similar before and after vitrectomy and in eyes with an intact vitreous body or with extensive vitreous liquefaction.

It has been argued that the loss of the gel structure of the vitreous body, as a consequence of vitrectomy or age-related liquefaction, has important effects on the distribution of small molecules in the eye (Stefansson et al. 1990; Harocopos et al. 2004; Stefansson 2006). The available evidence suggests that the increased rate at which molecules are redistributed in the vitreous compartment in the absence of the vitreous gel or after vitreous degeneration is more likely to be because of an increase in fluid circulation than a difference in the rate of diffusion.