Thermal depth profiling of vascular lesions: automated regularization of reconstruction algorithms

Abstract

Pulsed photo-thermal radiometry (PPTR) is a non-invasive, non-contact diagnostic technique used to locate cutaneous chromophores such as melanin (epidermis) and hemoglobin (vascular structures). Clinical utility of PPTR is limited because it typically requires trained user intervention to regularize the inversion solution. Herein, the feasibility of automated regularization was studied. A second objective of this study was to depart from modeling port wine stain PWS, a vascular skin lesion frequently studied with PPTR, as strictly layered structures since this may influence conclusions regarding PPTR reconstruction quality. Average blood vessel depths, diameters and densities derived from histology of 30 PWS patients were used to generate 15 randomized lesion geometries for which we simulated PPTR signals. Reconstruction accuracy for subjective regularization was compared with that for automated regularization methods. The objective regularization approach performed better. However, the average difference was much smaller than the variation between the 15 simulated profiles. Reconstruction quality depended more on the actual profile to be reconstructed than on the reconstruction algorithm or regularization method. Similar, or better, accuracy reconstructions can be achieved with an automated regularization procedure which enhances prospects for user friendly implementation of PPTR to optimize laser therapy on an individual patient basis.

Introduction

Most port wine stains (PWS), congenital vascular malformations of human skin, are still resistant, or respond poorly to laser therapy while a sub-group of lesions responds quite satisfactorily. It is believed that the vast heterogeneity in PWS lesion characteristics such as depth and diameter of ecstatic vessels are the underlying cause for the highly variable and unpredictable response to laser therapy. A suitable diagnostic technique may enable physicians to make a knowledge-based choice regarding laser wavelength, pulse duration and radiant exposure in an effort to optimize therapy on an individual patient basis.

Pulsed photo-thermal radiometry (PPTR) is a non-contact technique in which skin is irradiated with laser light of sub-therapeutic radiant exposure and the temporal evolution of the surface radiometric temperature is measured with an infrared detector (Tam and Sullivan 1983, Imhof et al 1984). The laser light is selectively absorbed in subsurface chromophores such as epidermal melanin and hemoglobin in vascular structures causing a spatial distribution of temperature increases which are similar to those which occur during an actual therapeutic pulse. This spatial temperature distribution can then be determined by applying an inversion algorithm to the measured temporal evolution of the surface radiometric temperature.

PPTR has been considered a promising technique for PWS characterization because its contrast mechanism (optical absorption) is directly linked to the laser treatment mechanism: selective photo-thermolysis (Anderson and Parrish 1981, 1983). For example, the wavelength and pulse duration used for PPTR diagnostics are usually the same as those used for PWS laser therapy. PPTR, similar to photo-acoustic methods (Viator et al 2003, 2004), may thus have an important advantage over other candidate diagnostic methods which mostly rely on optical scattering (optical coherence tomography and reflectance spectrometry) and are thus only indirectly related to the therapeutic pulse.

Unfortunately, determination of the spatial temperature distribution from the measured radiometric signals is difficult. In mathematical terms, it is often described as a ‘severely ill-posed inverse problem’ which explains why a large number of inversion methods have been investigated (Jacques et al 1993, Milner et al 1995, 1996, Xiao and Imhof 1999, Xiao et al 2001, Cui et al 2003, Li et al 2004a, Verkruysse et al 2005). In simpler terms, the ‘ill-posedness’ means that an inversion algorithm produces several different spatial profiles as solutions to the measured temporal profiles. ‘Regularization’, a term describing the process of making an informed choice from the different spatial profiles is considered to be of critical importance in PPTR (Milner et al 1995, Li et al 2004a, Li et al 2004b, Verkruysse et al 2005). Many existing regularization techniques require some degree of skill by the user and are inherently subjective. For successful clinical implementation of PPTR, user intervention is undesirable. The first objective of this study is, therefore, to investigate if an objective, and thus automatable, regularization method can be used without compromising reconstruction accuracy.

As with any diagnostic method, it is important to have a realistic impression of the general accuracy of the diagnostic information. PPTR has been typically evaluated on a few rather simplified ‘layered’ PWS geometries (Milner et al 1995, Sathyam and Prahl 1997, Smithies et al 1998, Xiao and Imhof 1999, Xiao et al 2001, Majaron et al 2002, Cui et al 2003, Verkruysse et al 2005) on the basis of which it is not possible to determine PPTR’s ability to produce useful diagnostic information. Therefore, a second objective of this study is to rigorously and systematically test PPTR on a large number of realistic PWS geometries to allow different inversion and regularization methods to be objectively compared.

Methods

Simulation of PWS geometries and corresponding infra-red temporal signals

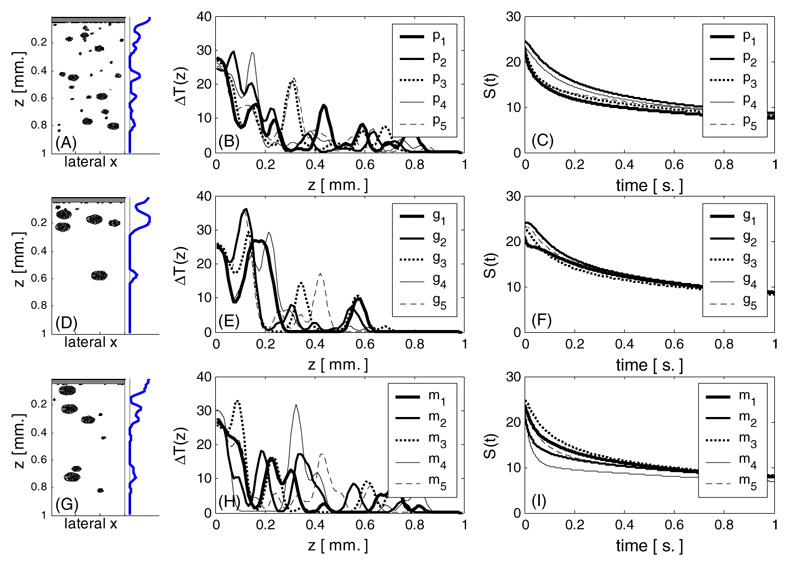
As a basis for ‘realistic’ PWS geometries, we chose to use data published by Fiskerstrand et al (1996) in which histological data of 32 PWS patients were stratified by response to laser treatment. The resulting data for each response group were presented as distributions of vessel diameter and depth. Under the assumption that no correlation exists between vessel depth, diameter and dermal blood volume fraction, this information allows us to simulate ‘realistic’ PWS vessel distributions. A simplification in our approach is that we assumed all vessels to be horizontally positioned and parallel to each other. Using the vessel diameter and depth distributions published by Fiskerstrand et al (1996) as a basis, we randomly resampled five geometries for each of the following response groups to laser treatment. Three resampled geometries are illustrated in figures 1(A), (D) and (G) for ‘poor’, ‘moderate’ and ‘good’ responders, respectively. The vessel positions were allowed to be positioned within a rectangle representing a lateral dimension of 0.3 mm and a depth dimension of 1 mm. The ‘poor’ responder geometries are characterized by a relatively large number of smaller vessels while the ‘good’ responders have vessels located at relatively shallow depths.

Figure 1.

(A) Simulated PWS geometry based on statistical characteristics for ‘poor responders’. (B) Temperature depth profile T for the geometry in (A) is indicated by the thick solid curve (‘p1’). Four additional profiles for ‘poor responders’ are included. (C) Temporal radiometric signals S for the temperature depth profiles in (B). (D), (E), (F) and (G), (H), (I) are similar to (A), (B) and (C) but were simulated for ‘good’ and ‘moderate responders’ respectively.

Subsequently, we used these vessel geometries as input to a Monte Carlo algorithm to compute energy deposition distributions, simulating a PPTR laser pulse. The skin depth in these simulations was 2 mm while the epidermal thickness and absorption coefficient were fixed at 60 µm and 16.2 cm⁻¹, respectively. Other skin optical properties used were the same as used in a previous study on light distributions using Monte Carlo for a laser wavelength of 585 nm (Verkruysse et al 1993). The Monte Carlo algorithm was adapted such that light exiting the 0.3 mm by 2 mm rectangle laterally re-enters the rectangle at the laterally opposite side, thus simulating a lateral repetition of the pattern in a semi-infinite layered geometry (Verkruysse et al 1999).

Herein, only one-dimensional PPTR was considered so the energy distribution was laterally averaged, obtaining a temperature increase (relative to the initial body temperature) versus skin depth profile, referred herein as ΔT (z, t = 0) or simply T. To account for the duration of the laser pulse, we allowed the T profiles to relax by modeling heat diffusion (using finite differences) for a period of 1.5 ms (a pulse duration often used in our PPTR measurements). The 15 generated temperature profiles are shown in figures 1(B), (E) and (H). For each T profile, the associated radiometric signal ΔS(t) or simply S was computed (shown in figures 1(C), (F) and (I)) using a well-described model (Milner et al 1995, Verkruysse et al 2005), described briefly in the following section. Finally, we created for each profile two additional signals by adding noise with corresponding signal-to-noise ratios (SNR) of 100 and 1000. The final result was a set of 45 simulated S(t) signals: 5 per each laser treatment response group and each at 3 SNR values of 100, 1000 and infinity.

Reconstruction algorithms and regularization methods

As described above, a relatively large number of reconstruction (inversion) algorithms as well as regularization methods have been previously proposed and used in the past. We chose to evaluate three different reconstruction algorithms (table 1). With each algorithm, we applied three different regularization approaches (table 2).

Table 1.

Reconstruction algorithms evaluated in this study.

Reconstruction algorithm	Type
Conjugate gradient minimization (CG)	Iterative
Singular value decomposition (SVDi)	Iterative
Singular value decomposition (SVDa)	Analytic

Table 2.

Regularization approaches evaluated in this study.

Regularization approach	Type
L-curve	Subjective, not automatable
RTnorm 0	Objective, automatable
RTnorm 1	Objective, automatable

In order to clarify the algorithms used in this study, a brief review of the fundamental equations involved is warranted and given below. The measured signal ΔS(t) can be expressed in terms of the temperature distribution ΔT (z, t = 0) and a kernel function K (z, t) (equation (1)). A detailed description of K (z, t) is given in multiple references (e.g. Verkruysse et al (2005)) and will therefore not be repeated here:

$$\mathrm{\Delta }S(t)={\displaystyle {\int }_{z=0}^{\infty }\mathrm{\Delta }T(z,t=0)K(z,t)dz.}$$ (1)

Equation (1) can conveniently be written as a simple matrix multiplication where ΔS(t), K(z, t) and ΔT (z, t = 0) are discretized as S, K and T, respectively:

$$\mathbf{\text{S}}=\mathbf{\text{K}}·\mathbf{\text{T}}.$$ (2)

Since T is the vector that displays the chromophore distribution, we wish to obtain this vector from S through an inversion algorithm. A brief description of the three algorithms used in this study is as follows.

Conjugate gradient (CG) minimization

This iterative method (Milner et al 1995) refers to a minimization algorithm and is used in our application to minimize the norm of the residue R (equation (3)),

$$\mathbf{R}=\parallel {\mathbf{S}}_{\text{meas}}-\mathbf{K}\mathbf{T}\parallel ,$$ (3)

where S_meas is the measured signal and the double bars indicate the Euclidean norm.

Hereafter, we refer to CG as the minimization algorithm that finds T by minimizing R. Regularization with this method is done by limiting the number of iteration steps.

SVD methods

Since the inverse problem is severely ill-posed, a simple inversion T = K⁻¹S results in highly variable results. However, in such cases, the pseudo-inverse of K using singular value decomposition (SVD) of K (equation (2)) is often used to express T in a straightforward way (Verkruysse et al 2005) (equation (4) and (equation 5)):

$$\mathbf{K}={\displaystyle \sum _{i=1}^m{\sigma }_i{\mathbf{u}}_i{\mathbf{v}}_i^T}$$ (4)

$${\mathbf{T}}^{(p)}={\displaystyle \sum _{i=1}^p{\mathrm{u}}_i^T\mathrm{S}{\mathrm{v}}_i}.$$ (5)

In this approach, regularization is easily implemented by limiting the number of p (i.e., the number of singular vectors u and v used in the composition of T^(p)). The desired vector describing the temperature immediately after laser exposure as a function of skin depth can thus easily be expressed in an analytical fashion.

Both CG and SVD methods often produce temperature profiles with negative values, which would correspond to temperature reductions as a result of laser exposure. Since this is clearly not realistic, the solutions are typically non-negatively (NN) constrained which has been demonstrated previously with CG (Milner et al 1995). We recently demonstrated (Verkruysse et al 2005) that a combination of SVD techniques with CG iteration can alsoimplement a NN constraint. The latter method has been described in detail (Verkruysse et al 2005) and will be referred to herein as SVD_i.

In this study, we introduce an alternative method that also uses SVD techniques but is analytical, i.e. non-iterative. This method will be referred to as SVD_a and implements the NN constraint in a very simple way by setting the negative values in T_(p) to 0. Regularization in SVD_i as well as SVD_a is done by limiting the number p, and often referred to as ‘Truncated SVD’

Regularization methods

Regularization is necessary for both iterative reconstruction algorithms such as CG and SVD. Over-iteration in CG and inclusion of too many singular vectors in SVD_i or SVD_a (too large a number for p) typically lead to unphysical oscillations in T (Milner et al 1995). Large oscillations cause the Euclidean norm of T (referred to herein as T_norm) to be very large, so T_norm can be used as a monitoring parameter in the regularization.

A popular regularization method known as the L-curve (Lawson and Hanson 1974) plots T_norm versus R (equation (3)). As the inversion procedure progresses (by iteration or incrementing the value of p), R decreases while T_norm increases. The resulting shape often resembles the letter ‘L’. The solution T associated with the ‘knee’ (the corner of the ‘L’) of the L-curve is supposedly optimal. Typically, the location of the ‘knee’ is subjectively assessed by an operator.

Unfortunately, the ‘knee’ is often not very sharp and, therefore, subjective bias introduced by different operators often leads to different ‘solutions’. In an attempt to make regularization objective, we introduce an alternative regularization method which is also based on the quantities R and T_norm. and we refer to this regularization method as RT_norm. In this approach, the product of R and T_norm is plotted versus the number of iterations for iterative reconstruction algorithms (Johnston and Gulrajani 2000) or the p value for SVD-based algorithms. When the product RT_norm is at a minimum we define this point as the end point for iteration and refer to this point as RT_norm0 or simply RT0. An alternative end point with this method and which was evaluated herein is defined by the iteration point at which RT_norm is 1% higher than the value at the minimum. This endpoint is referred to as RT_norm1 or simply RT₁. For the SVD methods, RT₀ and RT₁ are defined as the results for p at which RT_norm is at its minimum and p+1, respectively.

For the L-curve regularization, which is the only subjective regularization method in our study, the 45 simulated signals (15 profiles × 3 SNR levels) were offered to four trained individuals for reconstruction with each of the three reconstruction algorithms. Thus, a total of 540 (4 × 3 × 45) subjectively regularized profiles were produced. The total number of objectively regularized profiles was 270 (2 × 3 × 45), for 2 (RT₀ and RT₁) regularization methods and three reconstruction algorithms.

Quantification of reconstruction results

In order to compare objectively reconstructed profiles T with their corresponding original profiles T_orig, we define a parameter Q (equation (6)) as a measure of the reconstruction quality. Q is calculated as the average discrepancy between the original and reconstructed temperature increases. A Q value of 0 indicates a perfect reconstruction while larger Q-values indicate poor reconstructions.

Depending on the epidermal melanin concentration, the physician treating PWS may sometimes be more interested in an accurate prediction of the epidermal temperature rise during treatment, than PWS depth. Moreover, it is also expected that the temperature profiling accuracy decreases with depth (Smithies et al 1998). To account for this, we used exponential weighting functions ω (equation (6) and (equation 7)) with two different k values for the attenuation with depth: 0.05 and 0.4 mm for the epidermal temperatures and PWS reconstructions, respectively. The two different Q values for the two k values will be referred to as Q_epi and Q_PWS for ‘epidermal’ weighting and ‘PWS’ weighting respectively.

$$Q=\Vert \frac{{(\mathbf{T}-{\mathbf{T}}_{\text{orig}})}^2\omega }{\parallel \omega \parallel }\Vert$$ (6)

$$\omega =\text{exp}(-z/k).$$ (7)

A graphic example of the calculation of Q is shown in figure 2 using arbitrary examples of original and reconstructed temperature depth profiles.

Figure 2.

(A) Original temperature depth and an associated reconstructed temperature profile. (B) To quantify the discrepancy between original and reconstruction, the norm of the absolute difference is computed, weighted by a weighting curve being either ω_epi or ω_pws, emphasizing accuracy of the superficial chromophores and deeper chromophores, respectively (equation (6)). The resulting quality value Q is large and small for a poor and good reconstruction, respectively.

Results

From a total of 810 reconstructed profiles, we selected a small number that illustrates the impact of several of the study parameters on reconstruction quality. An example of how subjective regularization using the L-curve can lead to different reconstruction profiles is shown in figure 3(A). Two operators (a and b) determined the ‘knee’ to be at two different positions, leading to considerably different reconstruction profiles. Differences were also noted in reconstructed profiles when two different objective regularization methods (RT₀ and RT₁) are used as shown in figure 3(B). In this example, the inversion algorithm used is SVD_a and the values for p are 6 and 7 for RT0 and RT₁, respectively.

Figure 3.

(A) Original profile, simulated with ‘good responder’ characteristics, along with two reconstructions obtained with the CG inversion method and L-curve as regularization. The two reconstructed profiles are for two different operators who subjectively determined the ‘knee’ in the L-curve. (B) The same original profile as in (A), along with two reconstructed profiles obtained with SVD_a and regularization methods RT₀ and RT₁. RT₁ resulted in a better match with the original.

It is important to note that the illustrated differences between operators (figure 3(A)) are not typical. In fact, we found that for most profiles, the expected differences caused by subjectivity for the L-curve did not show up in a significant way, nor did we find an operator induced bias when all 15 profiles were considered. The superior reconstruction profile for RT₁ with respect to RT₀ with the SVDa algorithm was found to be significant on average only (paired, two tailed t-test, p < 0.05). There are many profiles for which RT₀ resulted in better profiles than RT₁. The overall comparisons of average reconstruction quality for the combinations will be discussed in the next section.

The reconstruction profiles shown in figure 4(A) are typical in the sense that there are no big differences in reconstruction quality for whichever combination of regularization and inversion methods was used in the presence of some noise in the signal S. Local chromophore concentrations at depths greater than approximately 0.1 mm could typically not be reconstructed very well. Examples of such features are the peaks at a depth of 0.3 mm in figure 4(A) and 0.2 and 0.35 mm in figure 4(B). However, depth determination of superficial peaks was generally determined well while the overall amplitude and shape were often reconstructed poorly.

Figure 4.

(A) Typical examples of reconstructed profiles in which temperature reconstruction close to the surface is better than that in the deeper dermis. Differences between inversion methods are marginal. (B) A second example in which two sharp peaks in the dermis are reconstructed as one broad layer. Differences between CG and SVD_a are small for SNR = 1000. When no noise is simulated, SVD_a can reconstruct the two peaks exceptionally well whereas for CG, the elimination of noise barely improved the reconstruction (not shown).

These features could typically not be resolved even in the absence of noise with all inversion algorithms with the exception of SVD_a in which the reconstruction profiles for infinite SNR matched the original profiles surprisingly well. An illustration of this is given by the dashed line in figure 4(B) showing that two peaks at 0.2 and 0.35 mm are resolved almost perfectly.

A surprising result is that the particular shape of a temperature profile affects the reconstruction quality more than any combination of regularization or inversion methods, and even the SNR level in the measured signal S. This is illustrated in figure 5 in which Q_epi values for all reconstructed profiles are plotted, categorized by SNR level (columns) and inversion algorithm (rows). For the L-curve regularization, the results for all four operators were averaged. The choice of the regularization method is virtually irrelevant for the CG and SVD_i methods. However, for SVD_a, the objective regularization approaches RT₀ and RT₁ are superior to the subjective L-curve method. Conclusions for Q_PWS (values not shown) are the same as for Q_epi.

Figure 5.

Reconstruction quality values Q_epi obtained for all 15 profiles for CG ((A)–(C)), SVD_a ((D)–(F)) and SVDi ((G)–(I)). The columns from left to right are for decreasing SNR levels as indicated. In each figure, the Q_epi values are shown for each of the three regularization methods studied. In (A), (B), (D) and (G), the values for the different regularization methods are so similar that the curves overlap partly or completely.

A final objective comparison between regularization and inversion methods can be made by considering the average of all Q values for the 15 profiles. The results are shown in figure 6 for quality metrics Q_epi and Q_PWS (figures 6(A)–(C) and (C)–(F), respectively) and for SNR = infinite, 1000 and 100. The observation that SVD_a performs well for infinite SNR is confirmed (figures 6(A) and (D)) while its advantage over CG and SVD_i disappears for SNR = 1000 (figures 6(B) and (E)) and SNR = 100 (figures 6(C) and (F)). While there are no significant differences between the regularization methods for CG and SVD_i, the L-curve and RT0 methods perform significantly worse (paired, two tailed t-test, p < 0.05) than RT1 when combined with SVD_a

Figure 6.

Quality values Q_epi ((A)–(C)) and Q_PWS ((C)–(E)) averaged over 15 profiles, categorized per regularization/inversion method combination. (A)/(D), (B/(E) and (C)/(F) are for SNR = infinite, 1000 and 100 respectively.

Values for Q_PWS are significantly higher than for Q_epi which reflect the fact that superficial chromophore concentrations (e.g. epidermal melanin) are reconstructed better than deeper chromophore concentrations (hemoglobin in blood vessels) (Smithies et al 1998).

Discussion

The first objective of this study was to evaluate if an objective regularization approach could be used in PPTR without compromising reconstruction quality. Our results indicate that this seems indeed possible. On average, reconstruction quality was even slightly better for the objective regularization approach (paired, two tailed t-test, p <0.05). The difference, however, is hardly relevant since it is considerably smaller than the variation in reconstruction quality caused by different PWS depth profiles.

The latter notion leads to the conclusion for our second aim which was to rigorously study PPTR using multiple realistic profiles. Our finding that the critical determinant of reconstruction quality is neither the regularization method nor the inversion algorithm but the particular shape of the simulated depth profile itself is somewhat surprising us, to our knowledge this has never been reported in the PPTR literature. In contrast, it was often tacitly assumed that the choice of regularization and inversion algorithms was critical because a certain choice will produce reconstructions of approximately equal quality, regardless of the actual depth profile. The simulations in this study show that the actual depth profile is more critical to the reconstruction accuracy than the inversion approach used.

It is important to note that the simulated ‘realistic’ profiles may represent only a small fraction of actual PWS geometries which were all simulated at 5% dermal blood volume fraction. Human PWS may have considerably lower as well as higher dermal blood volume fractions. It is possible that conclusions derived from this study may not hold had variation in this parameter been modeled. Similarly, if the lateral dimension of the rectangle in which we resampled the PWS geometries had been larger than the 0.3 mm as used in this study, the original profiles T_orig would have shown fewer features which would likely have affected the Q values. In typical PPTR measurements, the interrogated areas are typically larger. However, we chose the relatively small lateral dimension because we wanted to test the reconstruction methods with ‘feature rich’ profiles.

Majaron et al (2002) demonstrated that 2 wavelength excitation PPTR can enhance the accuracy of reconstructed temperatures by separating the epidermal signal from that of underlying vascular structures. A study similar to the present one for 2 wavelength excitation is important and being performed at our institute.

The definition of Q is somewhat arbitrary and does not necessarily reflect whether the depth location of a chromophore ‘peak’ is reconstructed accurately. We tried briefly to incorporate the depth accuracy of a chromophore peak in the reconstruction quality parameter to meet the physician’s need to know PWS ‘depth’. However, this proved cumbersome because very often the depth location of a peak shifts dramatically or a peak may even disappear with a small difference in regularization. This is illustrated in figure 4(B) where the reconstruction profile for CG is not appreciably different from that obtained with SVD_a (SNR = 1000) while the curve for CG would have defined only one peak at 0.35 mm depth and the SVD_a curve would have defined two peaks. However, despite its limitations, we believe that our definition of Q is sufficient to support the general conclusions of this study.

The differentiation between Q_epi and Q_PWS shows that PPTR provides significantly more accurate predictions for the epidermal temperature increase in response to pulsed laser exposure than for deeper skin layers. This suggests that the value of PPTR may be to provide the physician with guidelines regarding the maximum safe radiant exposure (the epidermal temperature increase is the main limitation in terms of maximizing radiant exposure) rather than to inform about PWS ‘depth’ or even peak temperatures in a reconstructed vessel or ‘layer’ of vessels. In this context, it is important to keep in mind that one-dimensional PPTR by definition provides an estimate for the average temperature increase at a certain depth. The actual temperature in vascular structures is likely to be much higher while the peri-vascular dermis experiences much lower temperature increases than indicated by the PPTR reconstruction profile. In our institute we are currently indeed focusing our efforts to relate PPTR-obtained information on the maximum safe laser radiant exposures as opposed to predicting PWS ‘depth’ (Verkruysse et al 2007).

There are many other ways to approach the inverse problem of PPTR and this study does not claim that the studied algorithms are optimal or even close to optimal. However, the finding that reconstruction quality for all three algorithms, almost independent of the regularization mechanism, depends strongly on the actual profile to be reconstructed suggests that in the evaluation of solutions to the inverse problem of PPTR, it is important to model more realistic profiles than simple discrete layers of chromophores as has been done typically.

Conclusions

The goal of this study was to test if PPTR depth profiling accuracy is compromised when objective rather than subjective regularization methods are used. Objective regularization methods performed equally well in this study, if not better than the more conventional subjective L-curve method. Reconstruction quality of simulated one-dimensional depth profiles of realistic PWS geometries depends on the actual shapes of the profiles rather than the combination of regularization and inversion methods.