Abstract
The villin headpiece subdomain (HP36) is a widely used system for protein-folding studies. Nuclear magnetic resonance cross-correlated relaxation rates arising from correlated fluctuations of two N-HN dipole-dipole interactions involving successive residues were measured at two temperatures at which HP36 is at least 99% folded. The experiment revealed the presence of motions slower than overall tumbling of the molecule. Based on the theoretical analysis of the spectral densities we show that the structural and dynamic contributions to the experimental cross-correlated relaxation rate can be separated under certain conditions. As a result, dynamic cross-correlated order parameters describing slow microsecond-to-millisecond motions of N-H bonds in neighboring residues can be introduced for any extent of correlations in the fluctuations of the two bond vectors. These dynamic cross-correlated order parameters have been extracted for HP36. The comparison of their values at two different temperatures indicates that when the temperature is raised, slow motions increase in amplitude. The increased amplitude of these fluctuations may reflect the presence of processes directly preceding the unfolding of the protein.
INTRODUCTION
Dynamics of biological molecules are recognized to play an important role in many biological processes. Dynamics of proteins occur on a wide range of timescales and a variety of nuclear magnetic resonance (NMR) techniques have been devised for its characterization (1–3). Slow microsecond-to-millisecond timescales dynamics have been shown to be essential for many protein functions and hence many recent works are geared toward elucidation of the details of slow motions (4–6).
One of the recognized techniques to probe slow timescale dynamics is residual dipolar coupling (RDC) experiments (7,8). However, applications of this technique require sample preparation strategies in several orienting media (7,8).
A number of cross-correlated relaxation experiments (3,9,10) allowing one to study slow motions of various nuclei have been developed. In this work, we utilize a technique developed by Pelupessy et al. (11) for investigation of correlated fluctuations of NH bonds in neighboring amino acids. The technique relies on the measurements of cross-correlated relaxation rates caused by the fluctuations of two N-H dipole-dipole interactions that depend on the fluctuation of the angle between corresponding N-H bond vectors. Different timescales of motions contribute to the rate. Since the characterization of fast picosecond-to-nanosecond motions can be done using 15N laboratory frame relaxation techniques, this experiment allows direct separation of fast and slow dynamics.
As has been long recognized (12–17), in addition to dynamic information, cross-correlated relaxation rates depend on structural parameters. In the case of the dipole-dipole cross-correlated relaxation experiment, they depend on the structural angles between two N-H bonds in neighboring residues. The angles can be usually obtained from either the x-ray or NMR structure of a protein. In practice, the values of the angles obtained from each of these structural techniques can deviate significantly, and in this case, cross-correlation experiments can provide additional information for validation of a protein structure.
In this work, we analyze slow microsecond-to-millisecond dynamics involving successive residues in the chicken villin headpiece C-terminal subdomain (HP36). Villin is an F-actin bundling protein involved in the maintenance of the microvilli of the absorptive epithelia (18,19). Villin headpiece subdomain is a 35-residue, autonomously folding, thermostable motif at the extreme C-terminus of villin (20). The subdomain spans residues 42–76 (residues 791–825 of intact chicken villin) of the full-length 76-amino-acid residue villin headpiece. The recombinant form of the subdomain (HP36) has an additional N-terminal methionine residue designated arbitrarily as residue 41.
HP36 is one of the smallest known examples of a cooperatively folded domain of a naturally occurring protein. This small protein is a very popular system for computational and experimental protein folding studies (20–31). The structure of HP36, as determined by x-ray and NMR spectroscopy (32,33), consists of three short helices (residues 44–51, 54–60, and 64–74) surrounding a tightly packed hydrophobic core. Fig. 1 shows a ribbon diagram of the protein. Wickstrom et al. (34) conducted a molecular dynamics study that indicated that the x-ray structure is a better representation of the folded state at neutral pH compared to the NMR structure based on backbone conformation, core packing, C-capping motif, and side-chain packing interactions. Backbone dynamics on the fast picosecond-to-nanosecond timescale has been analyzed earlier using 15N laboratory frame relaxation experiments (35).
FIGURE 1.

MolScript (57) diagram of 36-residue headpiece subdomain of F-actin binding protein villin (HP36). Helices are in black. N-terminus is on the left.
The cross-correlated relaxation measurements described below were performed at two different temperatures at which HP36 is at least 99% folded. In the Theory subsection, we relate the experimental NMR cross-correlated relaxation rates to the amplitudes of backbone motions in the presence of fast and slow backbone dynamics. We show that in the limit when the timescale of the slow motions τs significantly exceeds the timescale of the overall molecular tumbling τc, the slow motion cross-correlated order parameters depend on the interbond correlation and represent an ensemble average of a certain function of interbond angles over all possible conformations. We also show how to separate the cross-correlated order parameter into the structural and dynamic contributions.
Earlier works on anisotropic interactions (i.e., dipolar and chemical shift anisotropy) considered either the opposite limit τs ≪ τc (36) or only uncorrelated slow motions (37). In contrast, we show how the experimental rates can be used to obtain information on the amplitudes of slow microsecond-to-millisecond fluctuations of the angles between two N-H bonds in neighboring residues for any extent of interbond correlations.
By comparing theory with experiment, we obtain the values of dynamic slow motion cross-correlated order parameters, introduced in this work, and show that the average amplitude of slow backbone motions involving successive NH bonds increases with temperature. In addition, we show that our data provides further evidence for the validation of the high-resolution x-ray structure as closer to the actual structure of the protein in solution.
MATERIALS AND METHODS
Sample preparation
The experiments were performed on 15N/13C labeled villin headpiece subdomain expressed according to the procedure described in Bi et al. (38). The essence of the procedure consists of linking HP36 via a factor Xa cleavage sequence to the C-terminus of the N-terminal domain of the ribosomal protein L9. The following modifications were used: the protein was expressed in minimal media with 0.8 g/ml 15NH4Cl and 3 g/ml 13C-glucose. A G50 column (size 2 cm × 100 cm) with 20 mM Tris, 100 mM NaCl, 5 mM CaCl2, and 0.01% azide buffer at pH 7.5 was used for a first purification step, followed by a cleavage by factor Xa. The cleavage was performed at room temperature with eight units of factor Xa per mg of protein. The product was lyophilized and purified by reverse-phase high performance liquid chromatography. The identity and purity of the sample was confirmed by mass spectroscopy, N-terminal sequencing, 15N NMR HSQC spectrum, and reverse-phase high performance liquid chromatography.
The protein was dissolved in 350 μL of 90% H2O/10% D2O to a concentration of 1.4 mM with 50 mM sodium acetate-d3 buffer and the pH was adjusted to 5.4. A Shigemi tube made of susceptibility-matched glass was used.
NMR spectroscopy
The experiment for the measurements of NH/NH dipole-dipole cross-correlated relaxation rates is based on the interconversion between the double quantum (DQ) coherences:  and
and 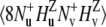 (11). The main mechanism of the interconversion is due to correlated fluctuations of the dipole-dipole interactions between hydrogen and nitrogen spins (NuHu and NvHv). In principle, the rates can also be measured using both DQ and ZQ coherences. However, by selecting only the DQ coherence, one avoids the effects of cross-relaxation involving the two amide protons.
(11). The main mechanism of the interconversion is due to correlated fluctuations of the dipole-dipole interactions between hydrogen and nitrogen spins (NuHu and NvHv). In principle, the rates can also be measured using both DQ and ZQ coherences. However, by selecting only the DQ coherence, one avoids the effects of cross-relaxation involving the two amide protons.
The rates 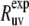 are obtained from the results of two experiments. In the first experiment, the decay of the initial coherence
are obtained from the results of two experiments. In the first experiment, the decay of the initial coherence 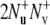 is detected and the volumes of the peaks in the resulting spectrum Iref are taken. In the second experiment, the coherence resulting from the two dipole-dipole interactions
is detected and the volumes of the peaks in the resulting spectrum Iref are taken. In the second experiment, the coherence resulting from the two dipole-dipole interactions  is detected. The volumes of the resulting peaks in the spectrum are denoted by Icross. The intensities Icross and Iref are proportional to the expectation values
is detected. The volumes of the resulting peaks in the spectrum are denoted by Icross. The intensities Icross and Iref are proportional to the expectation values 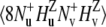 and
and 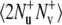 operators, respectively.
operators, respectively.
The rate 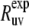 is then obtained from the ratio of Icross and Iref,
is then obtained from the ratio of Icross and Iref,
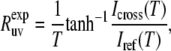 |
(1) |
where T is a relaxation delay.
Note that for a specific residue the magnetization transfer starts from the amide proton 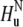 and INEPT-like transfers are utilized to create the double-quantum coherence
and INEPT-like transfers are utilized to create the double-quantum coherence 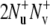 involving two nitrogen spins in successive residues. After the relaxation period, the magnetization is returned to the original amide proton
involving two nitrogen spins in successive residues. After the relaxation period, the magnetization is returned to the original amide proton 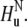 Thus, for a residue i, correlations are seen only with the successive residue i + 1.
Thus, for a residue i, correlations are seen only with the successive residue i + 1.
The NMR data were acquired on a Bruker DMX spectrometer (Bruker Biospin, Billerica, MA) operating at 500.13 MHz and equipped with a triple resonance TBI probe (Bruker) with triple axes gradients. The experiments were performed at 22 and 32°C. One-hundred percent methanol and ethylene glycol samples were used for temperature calibration (39). Data were acquired with a single relaxation delay of 43 ms. Two-dimensional spectra were acquired in an interleaved manner with 256 scans for the reference and 1536 for the cross-peak experiments. A quantity of 512 × 32 complex points were collected with a spectral width of 14 and 25 ppm in the 1H and 15N dimensions, respectively. Three data sets were taken for each of the temperature conditions and the data reported represents the average of the three data sets. Acquisition times were 13 days for each temperature.
The data were processed by the NmrPipe/NmrDraw/NlinLS package (40). 15N and 1H assignments were taken from a previous report (20). Typical errors in the NH-NH angles calculated from the NMR structure were obtained from the ensemble of the 29 structures (available at http://people.bu.edu/cjmck/pdb). To estimate typical errors in the angles calculated from the x-ray structure we compared five different x-ray structures for various mutants of HP36 corresponding to PDB entries 1YRF, 1WY3, 1WY4, 1YRI, and 2F4K (25,33). The errors in the cross-correlated order parameters, 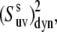 were calculated by the propagation of the errors in the cross-correlated relaxation rates.
were calculated by the propagation of the errors in the cross-correlated relaxation rates.
The absence of signals for the relatively large number of residues is due to an inherent insensitivity of the NH-NH cross-correlated experiments, which prevents the detection of residues with low signals. Three of the 36 residues are nondetectable: residue 62 is a proline, hence L61 and P62 cannot be detected. F76 cannot be detected since it is the last residue and does not have a neighboring amino acid on the right of the chain. In addition, the intensity of L42 in a regular HSQC spectrum is two to three times smaller compared to other residues in the protein and as a result, it was not observed in this experiment. The rest of the unobserved signals belong to loop residues or residues at the end of secondary structure regions. Likely reasons for signal losses for these residues will be discussed below.
RESULTS AND DISCUSSION
Theory
Slow motion cross-correlated order parameter in the limit τs ≫ τc
Cross-correlated relaxation is caused by concerted fluctuations of various interactions, such as dipole-dipole or chemical shift anisotropy (CSA). In our case, we are concerned with concerted fluctuations of dipole-dipole interactions for two NH bonds characterized by unit vectors u and v, which belong to successive amino acid residues. We will assume the existence of three timescales of motions: fast picosecond-to-nanosecond timescale (τf); slow millisecond-to-microsecond timescale (τs); and nanosecond timescale of the overall molecular tumbling (τc), such that τf ≪ τc ≪ τs.
The experimental cross-correlated relaxation rate 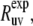 is proportional to spectral density at zero frequency, Juv(0) (3,11),
is proportional to spectral density at zero frequency, Juv(0) (3,11),
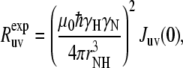 |
(2) |
where rNH is the distance between N and H nuclei, μ0 is the permeability of free space, and γH and γN are the gyromagnetic ratios for 1H and 15N, respectively,
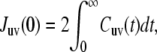 |
(3) |
where Cuv(t) is the cross-correlation function of the bond vectors fluctuations in the laboratory reference frame, and
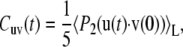 |
(4) |
where 〈…〉L denotes the thermal average over all possible configurations of the vectors u and v in the laboratory reference frame and P2(x) = (3x2 − 1)/2 is the second-order Legendre polynomial.
Equation 4 takes into account internal bond fluctuations as well as an overall molecular tumbling. The latter can be separated with the use of Lipari-Szabo decoupling approximation (41), which, for isotropic tumbling with the correlation time τc, leads to
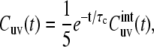 |
(5) |
where
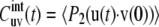 |
(6) |
is the two-bond cross correlation function, which takes into account only internal fluctuations of the bond vectors and 〈…〉 denotes the thermal average in the molecular reference frame. With u = v, Eqs. 4–6 define the autocorrelation function of single bond fluctuations.
To calculate 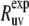 we will explore a two-component relaxation model introduced earlier (37). The fast component describes the relaxation of bond orientations on the timescale τf toward an intermediate quasiequilibrium state, characterized by an instantaneous random position of the slow fluctuating environment, which changes in an adiabatic manner. The slow component describes the relaxation of the bond environment to its equilibrium conformation. A similar two-component relaxational model has been considered by Clore et al. (42) and applied to the analysis of autocorrelated relaxation rates. However, the limit τs ≫ τc was not discussed.
we will explore a two-component relaxation model introduced earlier (37). The fast component describes the relaxation of bond orientations on the timescale τf toward an intermediate quasiequilibrium state, characterized by an instantaneous random position of the slow fluctuating environment, which changes in an adiabatic manner. The slow component describes the relaxation of the bond environment to its equilibrium conformation. A similar two-component relaxational model has been considered by Clore et al. (42) and applied to the analysis of autocorrelated relaxation rates. However, the limit τs ≫ τc was not discussed.
Note that the formalism proposed below for the derivation of the spectral density Juv(0) in the limit τf ≪ τc ≪ τs is different from the one employed in the earlier work (37) based on the coupled single exponential kinetic equations for the correlation functions of the fast and slow motions. We will show that the spectral density expression can be obtained without invoking any particular form for the time evolution of the cross-correlation function 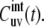 This is especially important for slow motions, since they are likely not to follow a single exponential relaxation.
This is especially important for slow motions, since they are likely not to follow a single exponential relaxation.
Since Cuv(t) in Eq. 5 is proportional to exp(−t/τc), the main contribution to the integral in Eq. 3 originates from the time interval t ∼ τc ≫ τf, where each bond vector is already in the quasiequilibrium state described above.
It is convenient to rewrite Eq. 6 in the form
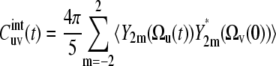 |
(7) |
using the addition theorem for spherical harmonics, where Ωu and Ωv are the solid angles describing the positions of the vectors u and v in the molecular reference frame. The spherical harmonics Y2m(Ωu) and Y2m(Ωv) can be expressed in the slowly fluctuating local environment reference frame as
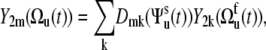 |
(8) |
where 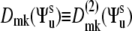 are the second-rank Wigner matrix elements and
are the second-rank Wigner matrix elements and 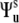 represents the three Euler angles relating the bond local environment reference frame to the molecular reference frame;
represents the three Euler angles relating the bond local environment reference frame to the molecular reference frame; 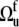 is the solid angle characterizing the direction of the bond vector with respect to the local environment reference frame.
is the solid angle characterizing the direction of the bond vector with respect to the local environment reference frame.
As shown recently (43,44), interbond interactions impose certain constrains on the bond vector fluctuation on the timescale τf, and renormalize the values of the Lipari-Szabo order parameters. In the derivation below, we assume that the values 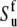 and
and 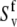 can be independently extracted from NMR autorelaxation experiments. For t ≫ τf, the correlations between the components
can be independently extracted from NMR autorelaxation experiments. For t ≫ τf, the correlations between the components 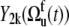 and
and 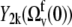 vanish. According to the definition of the quasiequilibrium state above, they can be replaced by their average values
vanish. According to the definition of the quasiequilibrium state above, they can be replaced by their average values 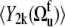 and
and 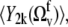 respectively.
respectively.
Assuming also the axial symmetry of the fast fluctuations with respect to the local environment axis we have 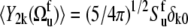 (δk0 is the Krönecker symbol and
(δk0 is the Krönecker symbol and 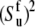 is the Lipari-Szabo autocorrelated order parameter for fast motions (41)) and therefore, only the component
is the Lipari-Szabo autocorrelated order parameter for fast motions (41)) and therefore, only the component 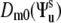 contributes to Eq. 8. Since Dm0 does not depend on the third Euler angle, the latter could be set to zero and the first two Euler angles represent the solid angle
contributes to Eq. 8. Since Dm0 does not depend on the third Euler angle, the latter could be set to zero and the first two Euler angles represent the solid angle 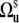 describing the orientation of the local environment axis with respect to the molecular reference frame. Then
describing the orientation of the local environment axis with respect to the molecular reference frame. Then 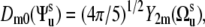 and we have
and we have
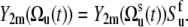 |
(9) |
Variables 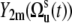 in Eq. 9 fluctuate slowly on the timescale τs ≫ τc. Therefore, due to the factor exp(−t/τc) in Eq. 5, which effectively restricts the integration in Eq. 3 to the values t ∼ τc, one can replace
in Eq. 9 fluctuate slowly on the timescale τs ≫ τc. Therefore, due to the factor exp(−t/τc) in Eq. 5, which effectively restricts the integration in Eq. 3 to the values t ∼ τc, one can replace 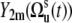 by
by 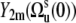 in Eq. 9.
in Eq. 9.
Thus, using Eqs. 3, 7, and 9 we obtain
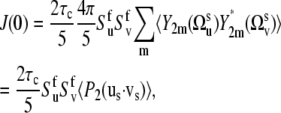 |
(10) |
where the vectors us and vs characterize the directions of the slow fluctuating local axes of the bonds' local environment. Equation 10 explicitly shows that, for the timescale τs ≫ τc, slow backbone motion contributes to the NMR cross-correlated relaxation rates via the statistical average of 〈P2(us · vs)〉 over all possible conformations characterized by different interbond angles. One can also see that there is no information on the exact values of internal correlation times of the slow motions.
In the absence of correlations of slow motions 〈P2(us · vs)〉 reduces to the form 〈P2(us · vs)〉 = 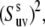 where
where
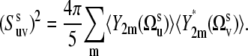 |
(11) |
Note that Eq. 11 has been obtained in the earlier work (37) with the use of the different formalism, but the effect of the interbond correlations on the NMR cross-correlated relaxation rates has not been analyzed. Equation 11 also defines the limit of the correlation function 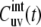 at t →∞,
at t →∞,
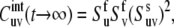 |
(12) |
provided that at t → ∞, the correlations are always decoupled. Note that for u = v, according to Eq. 7, 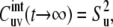 where
where
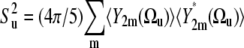 |
(13) |
is the order parameter characterizing the motional amplitude of the bond vector u in the molecular reference frame including both fast and slow motions. With the use of Eqs. 7 and12, we obtain the expression
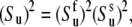 |
(14) |
where 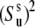 is the order parameter characterizing the amplitude of slow motion of the bond vector u. Note that Eq. 14 is identical with the expression of the generalized order parameter in the extended model free formalism obtained for the limit τf ≪ τs ≪ τc (42).
is the order parameter characterizing the amplitude of slow motion of the bond vector u. Note that Eq. 14 is identical with the expression of the generalized order parameter in the extended model free formalism obtained for the limit τf ≪ τs ≪ τc (42).
The limit of the correlation function given by Eq. 12 has been defined as the cross-correlated order parameter (36, 3). However, in the regime τc ≪ τs, Eqs. 11 and 12 do not capture the physics of correlated bond dynamics, and the quantity 〈P2(us · vs)〉 itself characterizes slow backbone motions. Therefore, 〈P2(us · vs)〉 has the meaning of a slow motion cross-correlated order parameter, provided it reduces to the earlier definition, Eq. 11, in the absence of correlations.
Separation of structural and dynamic contributions
If θuv is an instantaneous angle between the vectors us and vs, then 〈P2(us · vs)〉 in Eq. 10 equals to 〈P2(cos θuv)〉. This quantity contains both structural and dynamic contributions. A pure structural contribution corresponds to the rigid backbone for which the angle θuv has a fixed value 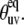 Dynamic contribution characterizes the effect of fluctuations of the angle θuv with
Dynamic contribution characterizes the effect of fluctuations of the angle θuv with 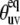 being the angle between equilibrium vectors
being the angle between equilibrium vectors 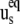 and
and 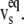
In the case of noncorrelated bond fluctuations, separation of 〈P2(cos θuv)〉 into the structural and dynamic contributions can be done exactly under the additional assumption of the axially symmetric slow fluctuations with respect to their equilibrium orientations. This can be shown by introducing the local equilibrium reference frames for vectors us and vs and presenting the components 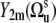 in the equilibrium reference frame as
in the equilibrium reference frame as
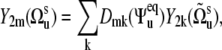 |
(15) |
where the Euler angles 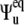 describe the orientation of the local equilibrium reference frame with respect to common molecular reference frame, and
describe the orientation of the local equilibrium reference frame with respect to common molecular reference frame, and 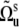 characterizes the direction of the slow fluctuating local axis with respect to its equilibrium reference frame. If fluctuations are axially symmetric with respect to the equilibrium axis, the terms with k ≠ 0 in Eq. 15 vanish. Then, using the addition theorem for spherical harmonics in analogy with Eqs. 9 and 10 we can rewrite Eq. 11 in the form
characterizes the direction of the slow fluctuating local axis with respect to its equilibrium reference frame. If fluctuations are axially symmetric with respect to the equilibrium axis, the terms with k ≠ 0 in Eq. 15 vanish. Then, using the addition theorem for spherical harmonics in analogy with Eqs. 9 and 10 we can rewrite Eq. 11 in the form
 |
(16) |
where  is the dynamic slow motion cross-correlated order parameter, which equals
is the dynamic slow motion cross-correlated order parameter, which equals
 |
(17) |
in the absence of correlations between the vectors us and vs. The parameters  are the local slow motion order parameters.
are the local slow motion order parameters.
Since 〈P2(cos θuv)〉 terms are directly measurable quantities in NMR cross-correlated relaxation experiments, an important question arises. To what extent can they be separated into the structural and dynamic contributions when the correlations between bond vectors are significant, such that Eq. 16 with the angle-independent order parameter 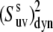 would be valid at least approximately with a controlled accuracy? We address this important question below.
would be valid at least approximately with a controlled accuracy? We address this important question below.
When Eq. 16 is valid, one can use experimental cross-correlation rates and knowledge of the structural angles, 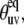 to extract information on the amplitude of correlated slow fluctuations, described by the dynamic cross-correlated order parameters
to extract information on the amplitude of correlated slow fluctuations, described by the dynamic cross-correlated order parameters 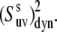
For the case of an intermediate degree of correlations between the two interactions, the decoupling given by Eq. 17 is not valid. Instead, we can write 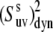 as
as
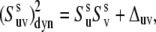 |
(18) |
where Δuv is a measure of the actual strength of the correlations between the local conformational fluctuations.
To illustrate the effect of the second term in Eq. 18, let us assume a very strong correlation in the slow motions of the two bond vectors such that θuv is fixed at a single value. This scenario is referred to as the rigid fragment. For this case 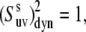 although the local order parameters
although the local order parameters 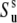 and
and 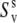 can still be <1. With intermediate strength of correlations, both terms in Eq. 18 can be of the same order of magnitude.
can still be <1. With intermediate strength of correlations, both terms in Eq. 18 can be of the same order of magnitude.
Under the assumption of the axial symmetry, the parameters 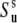 and
and 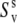 can be obtained from RDC experiments. Indeed, according to the model free approach (45), the definition of the RDC order parameter
can be obtained from RDC experiments. Indeed, according to the model free approach (45), the definition of the RDC order parameter 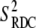 is identical with the definition of the order parameter
is identical with the definition of the order parameter 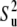 given in Eq. 13. Then using Eq. 14 and the axial symmetry approximation we obtain
given in Eq. 13. Then using Eq. 14 and the axial symmetry approximation we obtain 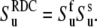 Further, if the correlations of the slow fluctuations of the two bond vectors are larger than the neglected nonaxial contributions, then the order parameters
Further, if the correlations of the slow fluctuations of the two bond vectors are larger than the neglected nonaxial contributions, then the order parameters 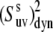 obtained from the cross-correlated relaxation experiment and the values of the single-bond local order parameters
obtained from the cross-correlated relaxation experiment and the values of the single-bond local order parameters 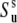 and
and 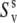 can be combined. This will give an estimate of the strength of the correlations in the slow motions of the neighboring bond-vectors, given by Δuv in Eq. 18. According to Meiler et al. (45) and Lakomek et al. (46), the extent of nonaxial contributions is expected to be small for residues belonging to α-helices and β-sheets, thus rendering the above analysis possible.
can be combined. This will give an estimate of the strength of the correlations in the slow motions of the neighboring bond-vectors, given by Δuv in Eq. 18. According to Meiler et al. (45) and Lakomek et al. (46), the extent of nonaxial contributions is expected to be small for residues belonging to α-helices and β-sheets, thus rendering the above analysis possible.
To determine the range of validity of Eq. 16 for correlated fluctuations of the bonds' local environment, we performed numerical simulations using the following simple model. According to its definition, 〈P2(cos θuv)〉 can be written as
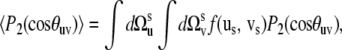 |
(19) |
where f (us, vs) is the probability density of finding the vectors us and vs at given orientations
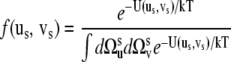 |
(20) |
and U(us, vs) is the potential energy constraining the amplitude of the fluctuations. For U(us, vs), we propose the form
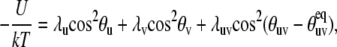 |
(21) |
where the first two terms describe axially symmetrical uncorrelated motions of the vectors us and vs with the parameters λu and λv characterizing the amplitudes of local restoring potentials. The values θu and θv are the angles describing instantaneous orientations of the vectors us and vs with respect to their local equilibrium axes. The third term is responsible for the correlation effects, the strength of which depends on the magnitude of the λuv. Purely uncorrelated motions correspond to the limit λuv = 0, and the opposite limit of strong correlations corresponds to λuv ≫ λu, λv.
Note that the local order parameters 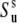 and
and 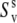 can be defined within the same model as
can be defined within the same model as
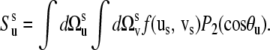 |
(22) |
The results of the numerical evaluation of 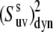 from Eqs. 16 and 19 are presented in Fig. 2. The values of λu, λv, and λuv have been chosen to satisfy the typical for NH bonds condition that the order parameters generally exceed 0.5 (46). As an example, the results of the simulations are presented for the values λu = λv, although almost the same numerical values of
from Eqs. 16 and 19 are presented in Fig. 2. The values of λu, λv, and λuv have been chosen to satisfy the typical for NH bonds condition that the order parameters generally exceed 0.5 (46). As an example, the results of the simulations are presented for the values λu = λv, although almost the same numerical values of 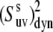 have been obtained for different combinations of λu and λv, as long as the product
have been obtained for different combinations of λu and λv, as long as the product 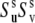 has been kept at the same value. The deviation of the curves from the straight lines characterizes the degree of the errors inherent in the definition of the dynamic order parameter according to Eq. 16.
has been kept at the same value. The deviation of the curves from the straight lines characterizes the degree of the errors inherent in the definition of the dynamic order parameter according to Eq. 16.
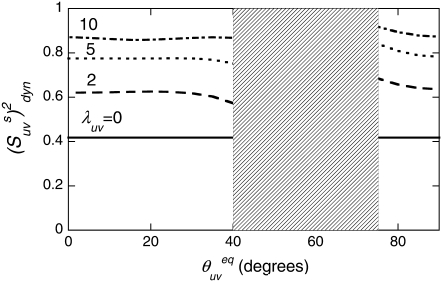
FIGURE 2.
Cross-correlated dynamic order parameters for slow motions 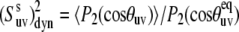 as a function of interbond angle
as a function of interbond angle 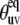 obtained by numerical simulations of the function 〈P2(cosθuv)〉 defined by Eq. 19. Parameters defining single bond potentials are λu = λv = 5. The values of λuv that define the interbond interactions are indicated on the graph. The shaded rectangle represents the range of angles for which the structural and dynamic contributions cannot be separated.
obtained by numerical simulations of the function 〈P2(cosθuv)〉 defined by Eq. 19. Parameters defining single bond potentials are λu = λv = 5. The values of λuv that define the interbond interactions are indicated on the graph. The shaded rectangle represents the range of angles for which the structural and dynamic contributions cannot be separated.
It follows from Fig. 2 that the uncertainties in 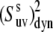 introduced by the approximate character of Eq. 16 do not exceed 5% for 0° <
introduced by the approximate character of Eq. 16 do not exceed 5% for 0° < 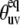 < 40° and 75° <
< 40° and 75° < 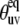 < 90° for the typical experimental values of
< 90° for the typical experimental values of 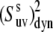 ≥ 0.7. In addition, the uncertainties are less for larger values of
≥ 0.7. In addition, the uncertainties are less for larger values of 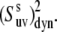
At the same time, the simulations show that the separation of the slow motion cross-correlated order parameter into the structural and dynamic contributions represents a poor approximation in the vicinity of the magic angle (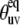 ≈ 54.7°), where P2(cos
≈ 54.7°), where P2(cos 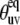 ) ≈ 0. Additionally, because of small values of 〈P2(cos θuv)〉 in this region, the experimental values
) ≈ 0. Additionally, because of small values of 〈P2(cos θuv)〉 in this region, the experimental values 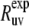 are also expected to be small, thus providing an additional obstacle for extraction of meaningful data.
are also expected to be small, thus providing an additional obstacle for extraction of meaningful data.
Validation of the protein structure
According to Eqs. 2, 10, and 16, the knowledge of the correct protein structure (which determines 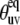 ) is crucial for a reliable determination of the slow motion cross-correlated order parameters from experimental cross-correlated relaxation rates.
) is crucial for a reliable determination of the slow motion cross-correlated order parameters from experimental cross-correlated relaxation rates.
The NMR structure of HP36 (32) was solved in 1997 using only two-dimensional homonuclear and 1H/15N heteronuclear methods. In contrast, the x-ray structure (33) is a high-resolution structure solved in 2005. The structures differ in the hydrophobic core packing, interhelical H-bonds, and in the length of the helices. Chiu et al. (33) notes that the differences between the x-ray and NMR structures are probably not caused by lattice contacts or crystal solution differences, but reflect the higher accuracy of x-ray structures.
The same conclusion was reached in Wickstrom et al. (34), where the authors conducted a molecular dynamics study of HP36 with explicit solvent using the NMR structure as a starting point. The simulations diverge from the initial NMR structure and spontaneously adopt a structure that is much more similar to the x-ray structure, suggesting that the x-ray structure is a more accurate representation of the structure in solution at neutral pH. However, as the authors noted, the simulation models they used can be limited in accuracy, and additional experiments would be desirable to test the theoretical predictions.
Below we use the NH-NH cross-correlated experiment as an independent tool for the validation of HP36 structure in solution. As has been first emphasized by Reif et al. (12), NMR cross-correlated relaxation experiments are sensitive methods for the validation/refinement of the protein structures. In the case of the NH-NH experiment, the technique can provide additional information regarding the values of the angle between successive NH bond vectors. Reif et al. considered a rigid limit corresponding to the absence of internal motions for which the experimental rate is given by
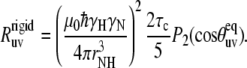 |
(23) |
In the presence of internal motions, a simple test to validate the protein structure determined by either NMR or x-ray techniques can be performed by comparing the experimental rates 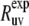 with the theoretical rates
with the theoretical rates 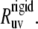 As follows from the discussion in the Theory subsection above, the ratios
As follows from the discussion in the Theory subsection above, the ratios 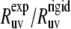 should satisfy the condition 0 ≤
should satisfy the condition 0 ≤ 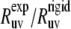 ≤ 1, except in the vicinity of the magic angle of 54.7°.
≤ 1, except in the vicinity of the magic angle of 54.7°.
In Table 1, we compare these ratios at 22°C using the angles calculated from the NMR and x-ray structures. The values of the angles are shown in Fig. 3.
TABLE 1.
Experimental cross-correlated relaxation rates for two N-H dipole-dipole interactions in successive residues in HP36 at 22 and 32°C and 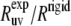 at 22°C
at 22°C
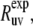 s−1 s−1
|
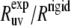 at 22°C at 22°C
|
|||
|---|---|---|---|---|
| Residue | 22°C | 32°C | NMR structure | X-ray structure |
| 44 | 2.97 ± 0.19 | 2.71 ± 0.21 | 0.81 ± 0.05 | 0.73 ± 0.05 |
| 45 | 2.54 ± 0.09 | 1.54 ± 0.04 | 0.66 ± 0.02 | 0.53 ± 0.02 |
| 46 | 2.88 ± 0.09 | 2.00 ± 0.07 | 0.62 ± 0.02 | 0.70 ± 0.02 |
| 47 | 3.43 ± 0.04 | 2.43 ± 0.01 | 0.70 ± 0.01 | 0.73 ± 0.01 |
| 48 | 2.79 ± 0.04 | 2.37 ± 0.04 | 0.71 ± 0.01 | 0.66 ± 0.01 |
| 49 | 2.69 ± 0.08 | 2.32 ± 0.32 | −1.01 ± 0.03 | 0.61 ± 0.02 |
| 50 | 2.95 ± 0.16 | 2.02 ± 0.01 | −1.66 ± 0.09 | 0.79 ± 0.04 |
| 53 | 3.85 ± 0.02 | 2.20 ± 0.12 | −5.05 ± 0.02 | 0.75 ± 0.01 |
| 55 | 3.19 ± 0.04 | 2.04 ± 0.28 | 0.72 ± 0.01 | 0.77 ± 0.01 |
| 57 | 3.23 ± 0.04 | 2.74 ± 0.05 | 0.80 ± 0.01 | 0.73 ± 0.01 |
| 58 | 2.94 ± 0.08 | 2.03 ± 0.09 | 0.96 ± 0.03 | 0.84 ± 0.02 |
| 59 | 1.48 ± 0.09 | 1.17 ± 0.08 | −0.58 ± 0.03 | 0.76 ± 0.04 |
| 63 | 2.79 ± 0.22 | 0.68 ± 0.05 | 0.66 ± 0.05 | |
| 65 | 2.54 ± 0.16 | 1.95 ± 0.01 | 0.93 ± 0.06 | 0.56 ± 0.03 |
| 66 | 3.34 ± 0.19 | 2.34 ± 0.01 | 0.68 ± 0.04 | 0.73 ± 0.04 |
| 67 | 3.30 ± 0.08 | 2.40 ± 0.09 | 1.00 ± 0.02 | 0.69 ± 0.02 |
| 68 | 3.32 ± 0.07 | 1.58 ± 0.08 | 0.64 ± 0.01 | 0.79 ± 0.02 |
| 69 | 3.07 ± 0.09 | 1.91 ± 0.12 | 1.01 ± 0.03 | 0.71 ± 0.02 |
| 70 | 3.30 ± 0.10 | 1.98 ± 0.12 | 0.68 ± 0.02 | 0.71 ± 0.02 |
| 71 | 3.17 ± 0.17 | 1.83 ± 0.10 | 1.20 ± 0.06 | 0.76 ± 0.04 |
| 72 | 2.08 ± 0.10 | 1.21 ± 0.08 | 0.60 ± 0.03 | 0.71 ± 0.03 |
| 73 | −1.32 ± 0.05 | −1.00 ± 0.05 | −0.28 ± 0.01 | 0.75 ± 0.03 |
Angles between two N-H bonds in successive residues used in the calculations of the Rrigid are taken from either NMR or high-resolution x-ray structure of HP36.
FIGURE 3.
Comparison of angles between two N-H bonds in successive residues, 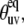 calculated using either NMR, 1VII.pdb (open squares) or x-ray, 1YRF.pdb (solid circles) structural coordinates. Helices are represented by zigzag lines and unstructured regions by straight lines. Typical uncertainties in the angles are 2° and 1.5° for NMR and x-ray structures, respectively.
calculated using either NMR, 1VII.pdb (open squares) or x-ray, 1YRF.pdb (solid circles) structural coordinates. Helices are represented by zigzag lines and unstructured regions by straight lines. Typical uncertainties in the angles are 2° and 1.5° for NMR and x-ray structures, respectively.
According to Fig. 3, large discrepancies in the values of 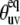 are observed for L42, A49, V50, F51, G52, M53, T54, A59, K73, G74, and L75. For all detectable residues from the above list, the ratios
are observed for L42, A49, V50, F51, G52, M53, T54, A59, K73, G74, and L75. For all detectable residues from the above list, the ratios 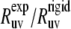 fall very far outside the theoretically expected limit when the angles are taken from the NMR structure. In fact, most of the values are negative. When the angles are taken from the x-ray structure, the ratios
fall very far outside the theoretically expected limit when the angles are taken from the NMR structure. In fact, most of the values are negative. When the angles are taken from the x-ray structure, the ratios 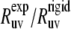 for all residues fall within the expected limits.
for all residues fall within the expected limits.
Note that the high-resolution x-ray structure that we refer to was obtained at neutral pH on a N68H mutant, whereas the NMR structure was obtained on a wild-type protein at pH 5.0. The HP36 sample (with the wild-type sequence) used in this study was at pH 5.4. Thus, despite the fact that experimental conditions of the cross-correlated experiment were closer to the conditions at which NMR structure was determined, our data provides further evidence that the high-resolution x-ray structure of HP36 is more accurate than the NMR structure.
Determination of slow motion cross-correlated order parameters
To extract the values of cross-correlated order parameters for slow motions from the experimental rates presented in Table 1, it is convenient to reduce Eqs. 2, 10, and 16 to the form
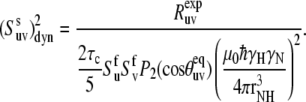 |
(24) |
The values of autocorrelated order parameters for fast motions 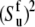 have been determined earlier at different temperatures (35). In the same study, HP36 was shown to undergo isotropic molecular tumbling. The equilibrium angles between successive NH bonds
have been determined earlier at different temperatures (35). In the same study, HP36 was shown to undergo isotropic molecular tumbling. The equilibrium angles between successive NH bonds 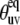 were calculated from the x-ray structure (see Fig. 3). Note that for almost all detectable residues the values of
were calculated from the x-ray structure (see Fig. 3). Note that for almost all detectable residues the values of 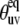 are outside the vicinity of the magic angle 54.7°, which according to the discussion in the Theory subsection justifies the separation of the order parameters into structural and dynamics contributions reflected in Eq. 24.
are outside the vicinity of the magic angle 54.7°, which according to the discussion in the Theory subsection justifies the separation of the order parameters into structural and dynamics contributions reflected in Eq. 24.
Many signals from residues belonging to loops and ends of the helices are within the noise level in the cross-correlated spectrum (represented by Icross in Eq. 1). In addition, they are either greatly reduced or completely within the noise level for the autocorrelated spectrum (represented by Iauto in Eq. 1). There are two major factors influencing the loss of the signal intensities. The first factor takes place during the lengthy magnetization transfer steps when coherence is transferred all the way along the polypeptide chain from the amide proton of one residue to the nitrogen of the neighboring residue. The signal is diminished due to enhanced relaxation of various coherences, likely because of more pronounced motions. The second factor takes place during the relaxation period, denoted by T in Eq. 1. Equation 1 demonstrates that the reduction of the signal intensity during the relaxation period is due to small cross-correlated rates. Small cross-correlated rates can come from either small values of the structural factor when the values of 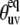 are close to the magic angle of 54.7° for which
are close to the magic angle of 54.7° for which 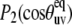 ≈ 0 or from small values of the
≈ 0 or from small values of the 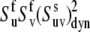 indicating high amplitude of motions. Among the absent loop residues, K75 is the only one with the angle being close to 54.7°. L42, L61, P62, and F76 are not observable. For the remainder of the missing loop residues (L43, S52, and T54) the absence of the signals are due to the dynamic contributions, taking place either during the lengthy magnetization transfer steps or the relaxation period itself. They are probably arising from large amplitude slow motions, since the autocorrelated 15N order parameters are comparable to those of other residues. Absent helical residues are F51, N60, and G74. All of them are at the very ends of the helices, which are likely to have strong dynamic contributions. Possible reasons are weaker H-bonds or their role as hinges between the structural elements and less ordered loops. In addition, F51 and N60 have structural angles close to 54.7°.
indicating high amplitude of motions. Among the absent loop residues, K75 is the only one with the angle being close to 54.7°. L42, L61, P62, and F76 are not observable. For the remainder of the missing loop residues (L43, S52, and T54) the absence of the signals are due to the dynamic contributions, taking place either during the lengthy magnetization transfer steps or the relaxation period itself. They are probably arising from large amplitude slow motions, since the autocorrelated 15N order parameters are comparable to those of other residues. Absent helical residues are F51, N60, and G74. All of them are at the very ends of the helices, which are likely to have strong dynamic contributions. Possible reasons are weaker H-bonds or their role as hinges between the structural elements and less ordered loops. In addition, F51 and N60 have structural angles close to 54.7°.
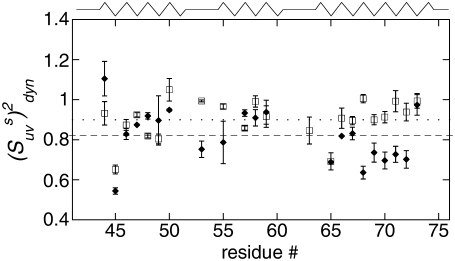
The values of 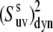 obtained with the use of Eq. 24 are shown in Fig. 4. Open square and solid diamond symbols represent the data at 22 and 32°C, respectively. Note that the midpoint of thermal unfolding transition is 72°C and 32°C is the highest temperature at which the HP36 is >99% folded (20). The results clearly demonstrate the presence of slow motions in HP36. However, as we already discussed in the Theory subsection above, the cross-correlated relaxation experiments do not provide the extent of correlations between the bonds participating in the slow motions. Additional RDC data would be desirable to clarify this question.
obtained with the use of Eq. 24 are shown in Fig. 4. Open square and solid diamond symbols represent the data at 22 and 32°C, respectively. Note that the midpoint of thermal unfolding transition is 72°C and 32°C is the highest temperature at which the HP36 is >99% folded (20). The results clearly demonstrate the presence of slow motions in HP36. However, as we already discussed in the Theory subsection above, the cross-correlated relaxation experiments do not provide the extent of correlations between the bonds participating in the slow motions. Additional RDC data would be desirable to clarify this question.
FIGURE 4.
Dynamic cross-correlated order parameters for slow motions of N-H bonds in neighboring amino acid residues 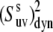 are plotted versus residues number at 22°C (open squares) and 32°C (solid diamonds). NH-NH angles between two N-H bonds in successive residues were calculated using the x-ray structure, 1YRF.pdb. Dotted (22°C) and dashed (32°C) lines represent the average values of
are plotted versus residues number at 22°C (open squares) and 32°C (solid diamonds). NH-NH angles between two N-H bonds in successive residues were calculated using the x-ray structure, 1YRF.pdb. Dotted (22°C) and dashed (32°C) lines represent the average values of 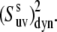
Uncertainties in the NH-NH angles provide an additional source of error for the values of 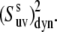 The average uncertainty in the angles for the x-ray structure, estimated as described in Materials and Methods, is ∼1.5°. The propagated errors in the values of
The average uncertainty in the angles for the x-ray structure, estimated as described in Materials and Methods, is ∼1.5°. The propagated errors in the values of 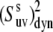 are functions of
are functions of  For example, the relative errors are 1, 5, 8, and 1% for 10, 30, 70, and 85°, respectively. The uncertainties are largest in the vicinity of the magic angle, which are excluded from our analysis.
For example, the relative errors are 1, 5, 8, and 1% for 10, 30, 70, and 85°, respectively. The uncertainties are largest in the vicinity of the magic angle, which are excluded from our analysis.
In determination of the order parameters for fast motions (35) the value of the chemical shift anisotropy was taken to be −172 ppm for all residues and the value rNH = 1.02 Å was used for the bond length. As has been discussed in detail elsewhere (47–53), the choice in the values of both CSA and bond-length affect the resulting values of autocorrelated order parameters. In contrast, the values of the cross-correlated order parameters for two dipole-dipole interactions are practically independent of the choice of the bond length, because the same factor 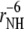 contributes to both autocorrelated dipole-dipole interactions, NuHu/NuHu and cross-correlated dipolar interactions of two successive bonds, NuHu/NvHv. The variations in NH bond lengths across the residues are absorbed in the effective values of
contributes to both autocorrelated dipole-dipole interactions, NuHu/NuHu and cross-correlated dipolar interactions of two successive bonds, NuHu/NvHv. The variations in NH bond lengths across the residues are absorbed in the effective values of 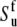 and
and 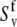 (54). If Eq. 24 uses the same bond length as employed for the model-free procedure (which yields
(54). If Eq. 24 uses the same bond length as employed for the model-free procedure (which yields 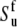 and
and 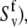 then the values of
then the values of 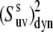 are essentially independent of the NH bond length. The uncertainty in CSA remains an essential factor in the effective value of the cross-correlated order parameter
are essentially independent of the NH bond length. The uncertainty in CSA remains an essential factor in the effective value of the cross-correlated order parameter 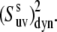 Hence, site-specific variations in CSA (which have not been taken into account in the determination of
Hence, site-specific variations in CSA (which have not been taken into account in the determination of 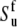 and
and 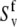 ) could introduce an additional small uncertainty of ∼3% or less (51) to the site-specific values of
) could introduce an additional small uncertainty of ∼3% or less (51) to the site-specific values of 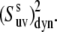 Taking into account all of the above discussions of the structural and 15N CSA uncertainties, we thus conclude that they have a small effect on the values of
Taking into account all of the above discussions of the structural and 15N CSA uncertainties, we thus conclude that they have a small effect on the values of 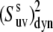 and the results presented in Fig. 4 are reliable estimates of the amplitudes of slow motions.
and the results presented in Fig. 4 are reliable estimates of the amplitudes of slow motions.
The effect of these uncertainties on the average values of the cross-correlated order parameters is even less significant. The average values of 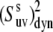 taken over all detectable residues are 0.90 ± 0.02 at 22°C and 0.82 ± 0.03 at 32°C. This result clearly indicates an average increase in the amplitude of the slow motions with increased temperature within this narrow temperature interval.
taken over all detectable residues are 0.90 ± 0.02 at 22°C and 0.82 ± 0.03 at 32°C. This result clearly indicates an average increase in the amplitude of the slow motions with increased temperature within this narrow temperature interval.
The ratio of dynamic order parameters at two temperatures is independent of structural uncertainties
As can be seen from Eq. 24 the ratio of 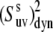 at any two temperatures can be determined without the knowledge of
at any two temperatures can be determined without the knowledge of 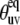 angles, assuming that the structure of a folded protein is temperature-independent. Thus, the ratio does not contain the uncertainties introduced by the uncertainties in the structure including the uncertainties in CSA parameters.
angles, assuming that the structure of a folded protein is temperature-independent. Thus, the ratio does not contain the uncertainties introduced by the uncertainties in the structure including the uncertainties in CSA parameters.
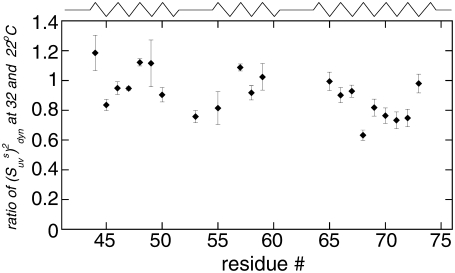
The ratio of 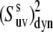 at 32°C and 22°C is displayed in Fig. 5. Most residues have a decrease in the values of slow motion cross-correlated order parameters at 32°C. This is most evident for residues in the third helix (residues 64–74). Order parameters for residues A49, A59, K65, and K73 do not change within the error limits and those for residues D44, K48, and A57 display a higher value at 32°C. The temperature-dependence of the dynamics is thus not homogenous across the sequence. The average value for the ratio is 1.01 ± 0.02 in helix 1, 0.92 ± 0.02 in helix 2, 0.83 ± 0.01 in helix 3, and 0.91 ± 0.01 for all residues in the protein.
at 32°C and 22°C is displayed in Fig. 5. Most residues have a decrease in the values of slow motion cross-correlated order parameters at 32°C. This is most evident for residues in the third helix (residues 64–74). Order parameters for residues A49, A59, K65, and K73 do not change within the error limits and those for residues D44, K48, and A57 display a higher value at 32°C. The temperature-dependence of the dynamics is thus not homogenous across the sequence. The average value for the ratio is 1.01 ± 0.02 in helix 1, 0.92 ± 0.02 in helix 2, 0.83 ± 0.01 in helix 3, and 0.91 ± 0.01 for all residues in the protein.
FIGURE 5.
Ratio of the dynamic cross-correlated order parameters 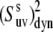 at 32 and 22°C. As explained in text, the ratio is independent of structural angles and reflects only the change in the N-H bonds dynamics with temperature.
at 32 and 22°C. As explained in text, the ratio is independent of structural angles and reflects only the change in the N-H bonds dynamics with temperature.
The decrease in the cross-correlated order parameters indicates that the slow motions of successive NH bonds become more pronounced at higher temperature. Similar features of backbone motions have been found for human ubiquitin protein (35). The increase in the amplitude of the slow motions can be viewed as indirect evidence for a larger population of states with higher free energies within the free energy landscape and reflect the onset of protein unfolding events, detected earlier by T-jumps experiments (55). Strong temperature dependence of the slow motion order parameters for the third helix suggests that it has a smaller stability compared to the other two helices. Thus, the denatured state ensemble of HP36 would be expected to have more structure in the first two helices compared to the third one. This is in agreement with the observations that the hydrophobic core of HP36 consists of residues F47, F51, and F58, which belong to the first two helices (56), and that a significant structure was observed in the HP21 peptide which spans helices 1 and 2 (22).
CONCLUSION
In this article, we investigated NMR cross-correlated relaxation rates arising from fluctuations of two N-HN dipole-dipole interactions in successive residues. These fluctuations correspond to the fast and slow internal backbone dynamics. We developed a theoretical framework which clarified the meaning of cross-correlated order parameters in the limit τf ≪ τc ≪ τs for any degree of correlations in the slow motions of the two bond vectors. Under certain conditions and with well-defined error limits, these order parameters can be separated into structural and dynamic contributions. As a result, we introduced the dynamic cross-correlated order parameter characterizing the amplitude of correlated slow motions. To estimate the actual strength of interbond correlations, we propose to combine cross-correlated relaxation and residual dipolar coupling experiments.
We applied the cross-correlated relaxation technique to extract the dynamic cross-correlated order parameters for HP36. The experimental data supports the notion that the high-resolution x-ray structure of HP36 is more accurate than the NMR structure. The ratio of the dynamic cross-correlated order parameters at different temperatures is independent of either the structural angles or the variations in the values of chemical shift anisotropies. The comparison of the dynamics indicates that for most residues in HP36 and especially in its last helix slow motions are more pronounced at higher temperatures where the protein remains >99% folded. The increased amplitude of slow motions can indicate the onset of protein unfolding events.
Acknowledgments
We are grateful to Prof. Arthur G. Palmer and Prof. Joel Tolman for critical readings of the manuscript. We thank Prof. Carlos Simmerling and Prof. Daniel P. Raleigh for useful discussions, Prof. W. M. Westler for assistance with the use of NMRFAM spectrometers, and to J. W. Brown, Dr. Z. G. Jiang, and Dr. S. Smirnov for assistance with HP36 preparation.
This work has been supported by the University of Alaska at Anchorage funds Nos. 104110-11970 and 14470 to L.V., and National Institutes of Health grant No. GM26335 to C.J.M. The study made use of the National Magnetic Resonance Facility at Madison, which is supported by National Institutes of Health grant Nos. P41RR02301 (Biomedical Research Technology Program/National Center for Research Resources) and P41GM66326 (National Institute of General Medical Sciences). Additional equipment was purchased with funds from the University of Wisconsin, the National Institutes of Health (grant Nos. RR02781 and RR08438), the National Science Foundation (grant Nos. DMB-8415048, OIA-9977486, and BIR-9214394), and the United States Department of Agriculture.
Editor: Heinrich Roder.
References
- 1.Palmer, A. G. 2004. NMR characterization of the dynamics of biomacromolecules. Chem. Rev. 104:3623–3640. [DOI] [PubMed] [Google Scholar]
- 2.Mittermaier, A., and L. E. Kay. 2006. Review. New tools provide new insights in NMR studies of protein dynamics. Science. 312:224–228. [DOI] [PubMed] [Google Scholar]
- 3.Frueh, D. 2002. Internal motions in proteins and interference effects in nuclear magnetic resonance. Prog. Nucl. Magn. Reson. Spectrosc. 41:305–324. [Google Scholar]
- 4.Bouvignies, G., P. Bernado, S. Meier, K. Cho, S. Grzesiek, R. Bruschweiler, and M. Blackledge. 2005. Identification of slow correlated motions in proteins using residual dipolar and hydrogen-bond scalar couplings. Proc. Natl. Acad. Sci. USA. 102:13885–13890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gardino, A. K., and D. Kern. 2007. Functional dynamics of response regulators using NMR relaxation techniques. Methods Enzymol. 423:149–165. [DOI] [PubMed] [Google Scholar]
- 6.Palmer, A. G., C. D. Kroenke, and J. P. Loria. 2001. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Methods Enzymol. 339:204–238. [DOI] [PubMed] [Google Scholar]
- 7.Tolman, J. R., and K. Ruan. 2006. NMR residual dipolar couplings as probes of biomolecular dynamics. Chem. Rev. 106:1720–1736. [DOI] [PubMed] [Google Scholar]
- 8.Blackledge, M. 2005. Recent progress in the study of biomolecular structure and dynamics in solution from residual dipolar couplings. Prog. Nucl. Magn. Reson. Spectrosc. 46:23–61. [Google Scholar]
- 9.Brutscher, B. 2000. Principles and applications of cross-correlated relaxation in biomolecules. Concepts Magn. Reson. 12:207–229. [Google Scholar]
- 10.Lundstrom, P., F. A. A. Mulder, and M. Akke. 2005. Correlated dynamics of consecutive residues reveal transient and cooperative unfolding of secondary structure in proteins. Proc. Natl. Acad. Sci. USA. 102:16984–16989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pelupessy, P., S. Ravindranathan, and G. Bodenhausen. 2003. Correlated motions of successive amide N-H bonds in proteins. J. Biomol. NMR. 25:265–280. [DOI] [PubMed] [Google Scholar]
- 12.Reif, B., M. Hennig, and C. Griesinger. 1997. Direct measurement of angles between bond vectors in high-resolution NMR. Science. 276:1230–1233. [DOI] [PubMed] [Google Scholar]
- 13.Reif, B., A. Diener, M. Hennig, M. Maurer, and C. Griesinger. 2000. Cross-correlated relaxation for the measurement of angles between tensorial interactions. J. Magn. Reson. 143:45–68. [DOI] [PubMed] [Google Scholar]
- 14.Schwalbe, H., T. Carlomagno, M. Hennig, J. Junker, B. Reif, C. Richter, and C. Griesinger. 2001. Cross-correlated relaxation for the measurement of angles between tensorial interactions. Methods Enzymol. 338:35–82. [DOI] [PubMed] [Google Scholar]
- 15.Chiarparin, E., P. Pelupessy, R. Ghose, and G. Bodenhausen. 2000. Relative orientation of (CH α)-H-α-bond vectors of successive residues in proteins through cross-correlated relaxation in NMR. J. Am. Chem. Soc. 122:1758–1761. [Google Scholar]
- 16.Ravindranathan, S., C. H. Kim, and G. Bodenhausen. 2003. Cross correlations between C-13-H-1 dipolar interactions and N-15 chemical shift anisotropy in nucleic acids. J. Biomol. NMR. 27:365–375. [DOI] [PubMed] [Google Scholar]
- 17.Rinnenthal, J., C. Richter, J. Ferner, E. Duchardt, and H. Schwalbe. 2007. Quantitative γ-HCNCH: determination of the glycosidic torsion angle χ in RNA oligonucleotides from the analysis of CH dipolar cross-correlated relaxation by solution NMR spectroscopy. J. Biomol. NMR. 39:17–29. [DOI] [PubMed] [Google Scholar]
- 18.Bretscher, A., and K. Weber. 1980. Villin is a major protein of the microvillus cytoskeleton which binds both G-actin and F-actin in a calcium-dependent manner. Cell. 20:839–847. [DOI] [PubMed] [Google Scholar]
- 19.Friederich, E., K. Van Compernolle, D. Louvard, and J. Van de Kerckhove. 1999. Villin function in the organization of the actin cytoskeleton—correlation of in vivo effects to its biochemical activities in vitro. J. Biol. Chem. 274:26751–26760. [DOI] [PubMed] [Google Scholar]
- 20.McKnight, C. J., D. S. Doering, P. T. Matsudaira, and P. S. Kim. 1996. A thermostable 35-residue subdomain within villin headpiece. J. Mol. Biol. 260:126–134. [DOI] [PubMed] [Google Scholar]
- 21.Brewer, S. H., D. M. Vu, Y. F. Tang, Y. Li, S. Franzen, D. P. Raleigh, and R. B. Dyer. 2005. Effect of modulating unfolded state structure on the folding kinetics of the villin headpiece subdomain. Proc. Natl. Acad. Sci. USA. 102:16662–16667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tang, Y. F., M. J. Goger, and D. P. Raleigh. 2006. NMR characterization of a peptide model provides evidence for significant structure in the unfolded state of the villin headpiece helical subdomain. Biochemistry. 45:6940–6946. [DOI] [PubMed] [Google Scholar]
- 23.De Mori, G. M. S., G. Colombo, and C. Micheletti. 2005. Study of the villin headpiece folding dynamics by combining coarse-grained Monte Carlo evolution and all-atom molecular dynamics. Proteins Struct. Funct. Bioinform. 58:459–471. [DOI] [PubMed] [Google Scholar]
- 24.Wickstrom, L., A. Okur, K. Song, V. Hornak, D. P. Raleigh, and C. L. Simmerling. 2006. The unfolded state of the villin headpiece helical subdomain: computational studies of the role of locally stabilized structure. J. Mol. Biol. 360:1094–1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kubelka, J., T. K. Chiu, D. R. Davies, W. A. Eaton, and J. Hofrichter. 2006. Sub-microsecond protein folding. J. Mol. Biol. 359:546–553. [DOI] [PubMed] [Google Scholar]
- 26.Buscaglia, M., J. Kubelka, W. A. Eaton, and J. Hofrichter. 2005. Determination of ultrafast protein folding rates from loop formation dynamics. J. Mol. Biol. 347:657–664. [DOI] [PubMed] [Google Scholar]
- 27.Havlin, R. H., and R. Tycko. 2005. Probing site-specific conformational distributions in protein folding with solid-state NMR. Proc. Natl. Acad. Sci. USA. 102:3284–3289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ripoll, D. R., J. A. Vila, and H. A. Scheraga. 2004. Folding of the villin headpiece subdomain from random structures. Analysis of the charge distribution as a function of pH. J. Mol. Biol. 339:915–925. [DOI] [PubMed] [Google Scholar]
- 29.van der Spoel, D., and E. Lindahl. 2003. Brute-force molecular dynamics simulations of villin headpiece: comparison with NMR parameters. J. Phys. Chem. B. 107:11178–11187. [Google Scholar]
- 30.Kubelka, J., W. A. Eaton, and J. Hofrichter. 2003. Experimental tests of villin subdomain folding simulations. J. Mol. Biol. 329:625–630. [DOI] [PubMed] [Google Scholar]
- 31.Wang, M. H., Y. F. Tang, S. S. Sato, L. Vugmeyster, C. J. McKnight, and D. P. Raleigh. 2003. Dynamic NMR line-shape analysis demonstrates that the villin headpiece subdomain folds on the microsecond time scale. J. Am. Chem. Soc. 125:6032–6033. [DOI] [PubMed] [Google Scholar]
- 32.McKnight, C. J., P. T. Matsudaira, and P. S. Kim. 1997. NMR structure of the 35-residue villin headpiece subdomain. Nat. Struct. Biol. 4:180–184. [DOI] [PubMed] [Google Scholar]
- 33.Chiu, T. K., J. Kubelka, R. Herbst-Irmer, W. A. Eaton, J. Hofrichter, and D. R. Davies. 2005. High-resolution x-ray crystal structures of the villin headpiece subdomain, an ultrafast folding protein. Proc. Natl. Acad. Sci. USA. 102:7517–7522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wickstrom, L., Y. Bi, V. Hornak, D. P. Raleigh, and C. Simmerling. 2007. Reconciling the solution and x-ray structures of the villin headpiece helical subdomain: molecular dynamics simulations and double mutant cycles reveal a stabilizing cation-π interaction. Biochemistry. 46:3624–3634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Vugmeyster, L., O. Trott, C. J. McKnight, D. P. Raleigh, and A. G. Palmer. 2002. Temperature-dependent dynamics of the villin headpiece helical subdomain, an unusually small thermostable protein. J. Mol. Biol. 320:841–854. [DOI] [PubMed] [Google Scholar]
- 36.Daragan, V. A., and K. H. Mayo. 1997. Motional model analyses of protein and peptide dynamics using C-13 and N-15 NMR relaxation. Prog. Nucl. Magn. Reson. Spectrosc. 31:63–105. [Google Scholar]
- 37.Vugmeyster, L., P. Pelupessy, B. E. Vugmeister, D. Abergel, and G. Bodenhausen. 2004. Cross-correlated relaxation in NMR of macromolecules in the presence of fast and slow internal dynamics. C. R. Phys. 5:377–386. [Google Scholar]
- 38.Bi, Y., Y. F. Tang, D. P. Raleigh, and J. H. Cho. 2006. Efficient high level expression of peptides and proteins as fusion proteins with the N-terminal domain of L9: application to the villin headpiece helical subdomain. Protein Expr. Purif. 47:234–240. [DOI] [PubMed] [Google Scholar]
- 39.Raiford, D. S., C. L. Fisk, and E. D. Becker. 1979. Calibration of methanol and ethylene-glycol nuclear magnetic-resonance thermometers. Anal. Chem. 51:2050–2051. [Google Scholar]
- 40.Delaglio, F., S. Grzesiek, G. W. Vuister, G. Zhu, J. Pfeifer, and A. Bax. 1995. Nmrpipe: a multidimensional spectral processing system based on UNIX pipes. J. Biomol. NMR. 6:277–293. [DOI] [PubMed] [Google Scholar]
- 41.Lipari, G., and A. Szabo. 1982. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 104:4546–4559. [Google Scholar]
- 42.Clore, G. M., A. Szabo, A. Bax, L. E. Kay, P. C. Driscoll, and A. M. Gronenborn. 1990. Deviations from the simple two-parameter model-free approach to the interpretation of N-15 nuclear magnetic-relaxation of proteins. J. Am. Chem. Soc. 112:4989–4991. [Google Scholar]
- 43.Ming, D. M., and R. Bruschweiler. 2006. Reorientational contact-weighted elastic network model for the prediction of protein dynamics: comparison with NMR relaxation. Biophys. J. 90:3382–3388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Abergel, D., and G. Bodenhausen. 2005. Predicting internal protein dynamics from structures using coupled networks of hindered rotators. J. Chem. Phys. 123:204901. [DOI] [PubMed] [Google Scholar]
- 45.Meiler, J., J. J. Prompers, W. Peti, C. Griesinger, and R. Bruschweiler. 2001. Model-free approach to the dynamic interpretation of residual dipolar couplings in globular proteins. J. Am. Chem. Soc. 123:6098–6107. [DOI] [PubMed] [Google Scholar]
- 46.Lakomek, N. A., T. Carlomagno, S. Becker, C. Griesinger, and J. Meiler. 2006. A thorough dynamic interpretation of residual dipolar couplings in ubiquitin. J. Biomol. NMR. 34:101–115. [DOI] [PubMed] [Google Scholar]
- 47.Tjandra, N., A. Szabo, and A. Bax. 1996. Protein backbone dynamics and N-15 chemical shift anisotropy from quantitative measurement of relaxation interference effects. J. Am. Chem. Soc. 118:6986–6991. [Google Scholar]
- 48.Fushman, D., and D. Cowburn. 1998. Model-independent analysis of N-15 chemical shift anisotropy from NMR relaxation data. ubiquitin as a test example. J. Am. Chem. Soc. 120:7109–7110. [Google Scholar]
- 49.Fushman, D., N. Tjandra, and D. Cowburn. 1998. Direct measurement of N-15 chemical shift anisotropy in solution. J. Am. Chem. Soc. 120:10947–10952. [Google Scholar]
- 50.Fushman, D., N. Tjandra, and D. Cowburn. 1999. An approach to direct determination of protein dynamics from N-15 NMR relaxation at multiple fields, independent of variable N-15 chemical shift anisotropy and chemical exchange contributions. J. Am. Chem. Soc. 121:8577–8582. [Google Scholar]
- 51.Hall, J. B., and D. Fushman. 2006. Variability of the N-15 chemical shielding tensors in the B3 domain of protein G from N-15 relaxation measurements at several fields. Implications for backbone order parameters. J. Am. Chem. Soc. 128:7855–7870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tang, S., and D. A. Case. 2007. Vibrational averaging of chemical shift anisotropies in model peptides. J. Biomol. NMR. 38:255–266. [DOI] [PubMed] [Google Scholar]
- 53.Kroenke, C. D., J. P. Loria, L. K. Lee, M. Rance, and A. G. Palmer. 1998. Longitudinal and transverse H-1-N-15 dipolar N-15 chemical shift anisotropy relaxation interference: unambiguous determination of rotational diffusion tensors and chemical exchange effects in biological macromolecules. J. Am. Chem. Soc. 120:7905–7915. [Google Scholar]
- 54.Kay, L. E., D. A. Torchia, and A. Bax. 1989. Backbone dynamics of proteins as studied by N-15 inverse detected heteronuclear NMR-spectroscopy—application to staphylococcal nuclease. Biochemistry. 28:8972–8979. [DOI] [PubMed] [Google Scholar]
- 55.Brewer, S. H., B. B. Song, D. P. Raleigh, and R. B. Dyer. 2007. Residue specific resolution of protein folding dynamics using isotope-edited infrared temperature jump spectroscopy. Biochemistry. 46:3279–3285. [DOI] [PubMed] [Google Scholar]
- 56.Frank, B. S., D. Vardar, D. A. Buckley, and C. J. McKnight. 2002. The role of aromatic residues in the hydrophobic core of the villin headpiece subdomain. Protein Sci. 11:680–687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Koradi, R., M. Billeter, and K. Wuthrich. 1996. MOLMOL: a program for display and analysis of macromolecular structures. J. Mol. Graph. 14:51–55. [DOI] [PubMed] [Google Scholar]