Modeling of the transient responses of the vocal fold lamina propria

Abstract

The human voice is produced by flow-induced self-sustained oscillation of the vocal fold lamina propria. The mechanical properties of vocal fold tissues are important for understanding phonation, including the time-dependent and transient changes in fundamental frequency (F₀). Cyclic uniaxial tensile tests were conducted on a group of specimens of the vocal fold lamina propria, including the superficial layer (vocal fold cover) (5 male, 5 female) and the deeper layers (vocal ligament) (6 male, 6 female). Results showed that the vocal fold lamina propria, like many other soft tissues, exhibits both elastic and viscous behavior. Specifically, the transient mechanical responses of cyclic stress relaxation and creep were observed. A three-network constitutive model composed of a hyperelastic equilibrium network in parallel with two viscoplastic time-dependent networks proves effective in characterizing the cyclic stress relaxation and creep behavior. For male vocal folds at a stretch of 1.4, significantly higher peak stress was found in the vocal ligament than in the vocal fold cover. Also, the male vocal ligament was significantly stiffer than the female vocal ligament. Our findings may help explain the mechanisms of some widely observed transient phenomena in F₀ regulation during phonation, such as the global declination in F₀ during the production of declarative sentences, and local F₀ changes such as overshoot and undershoot.

1. Introduction

Human phonation is produced when expiratory air flows through the vocal tract and causes the vocal folds to undergo self-sustained vibration. Figure 1 shows a laryngoscopic view of human larynx. The lamina propria of the vocal fold, which is the major vibratory tissue during phonation, is a layered connective tissue structure and can be divided into three layers from a histological perspective: the superficial layer, the intermediate layer and the deep layer. Functionally, these layers can be organized as the vocal fold cover (the epithelium and the superficial layer of the lamina propria) and the vocal ligament (the intermediate layer and the deep layer of the lamina propria). Key acoustic features of human phonation are defined so that they could be measured and studied quantitatively, e.g., the fundamental frequency (F₀) and the intensity of phonation. The fundamental frequency of human phonation is the fundamental frequency of vocal fold vibration; and the intensity of voice is closely related to the amplitude of vocal fold vibration. These acoustic characteristics are dictated by the vibration of the vocal fold. To improve our understanding of human phonation, an insight into the mechanical properties of the vocal fold lamina propria is thus indispensable.

Figure 1.

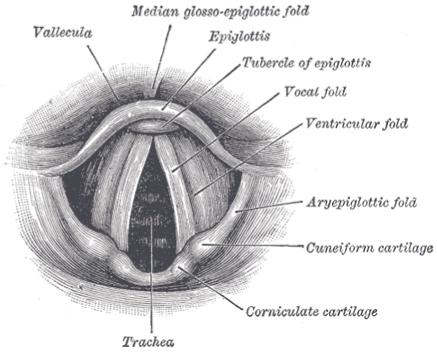
A laryngoscopic view of interior of human larynx, seen from the superior direction (Gray, 1918).

The vocal fold lamina propria has been characterized by both elastic and viscous mechanical behavior, including nonlinearity, hysteresis and time dependence (Min et al., 1995; Chan and Titze, 1999; Chan and Siegmund, 2004; Chan et al., 2007), as in other biological soft tissues (e.g., Woo et al., 1981; Hubbard and Chun, 1988; Schatzmann et al., 1998; Giles et al., 2007). Extensive studies have been conducted on the nonlinear elastic and hysteretic aspects of the stress-strain (or stress-stretch) response of the vocal fold. Min et al. (1995) proposed a nonlinear elastic model, which could capture the equilibrium stress-stretch response but failed to describe the hysteresis and rate-dependence of the vocal ligament. Viscoelastic models have been used to simulate the response of the vocal fold lamina propria under tensile or shear deformation (Chan and Titze, 2000; Chan and Siegmund, 2004; Hunter et al., 2004). In our previous study (Zhang et al., 2006), a two-network constitutive model was proposed to describe the stress-stretch response of the vocal fold lamina propria. The two-network model, which consists of a time-independent equilibrium network based on the Ogden’s model of hyperelasticity (Ogden, 1972) in parallel with a viscoplastic network, proved effective in characterizing the equilibrium stress-stretch response as well as the hysteretic response of the vocal fold cover in individual load cycles (Zhang et al., 2006).

Under cyclic mechanical loading of a soft tissue specimen transient effects appear. During cyclic tensile stretching and releasing of soft tissues, the peak stress decreases with the number of cycle, which is called cyclic stress relaxation. Repeated loading also results in a gradual increase in the reference length (or in situ, stress-free length) of the soft tissue specimen, which is a demonstration of creep behavior of the tissue. A large number of load cycles is often required for the stress to reach a steady state, which can be termed the “stabilized” or “preconditioned” state. The study of these transient biomechanical responses is relevant as they are required for some organs and tissue to function properly. For example, the transient effects of the myocardium might facilitate an increased stroke volume of diastole during exercise (Giles et al., 2007). In our previous study (Zhang et al., 2008) it was demonstrated that the transient mechanical response of the vocal fold tissue also can influence phonation processes.

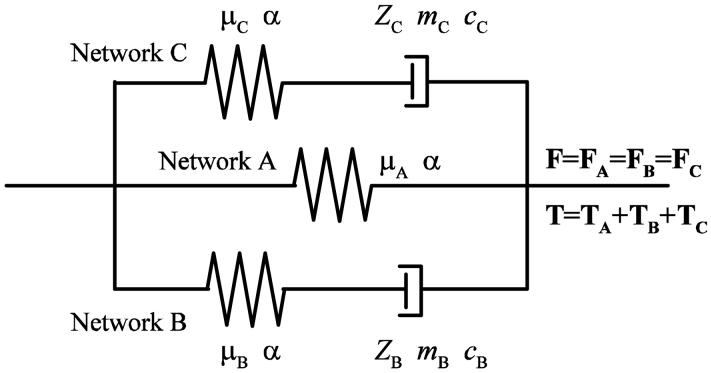
Transient responses of soft tissues have not commonly been characterized by constitutive models, most of which have focused on the stabilized state only. Only few studies (e.g., Woo et al., 1981; Carew et al., 2000; Giles et al., 2007) have made efforts to employ constitutive models to simulate such phenomena. Woo et al. (1981), Carew et al. (2000) and Giles et al. (2007) applied the quasi-linear viscoelasticity (QLV) theory (Fung, 1993) to simulate the preconditioning of the canine medial collateral ligament (MCL), the porcine aortic valve (PAV), and the porcine dermis. However, this theory has limitations in dealing with tissues with parallel fibers (Haut and Little, 1972; Jenkins and Little, 1974) and those with highly nonlinear response, especially in the large-strain time-dependent response. For these reasons, these models could not be applied for vocal fold tissues in the present study. Our previous two-network model (Zhang et al., 2006) focused on the hysteretic tissue response and failed to capture any long-term viscous behaviors, such as the peak stress decay and right-shift of the stress-stretch curves. The stress in the time-dependent network relaxed so quickly that it cannot provide the long-term cyclic stress relaxation observed empirically. To overcome this shortcoming of the two-network model, a three-network model with a long-term viscoplastic network in parallel with the two other networks is proposed (Fig. 2). This additional network is composed of a hyperelastic portion in series with a long-term viscoplastic portion, and is capable of relaxing its stress over a longer period of time. These two viscoplastic networks provide time constants on different scales, thus enabling the model to characterize both the short-term and the long-term viscous behaviors of the vocal fold lamina propria.

Figure 2.

A one-dimensional rheological representation of the three-network constitutive model, with a hyperelastic equilibrium network (A) in parallel with a short-term viscoplastic network (B) and a long-term viscoplastic network (C).

In the present study, the proposed three-network model is applied to simulate the cyclic stress-stretch responses of vocal fold cover and vocal ligament specimens from excised human larynges. The first stress-stretch cycle of each specimen is used to derive the parameters of the equilibrium network and the short-term viscoplastic network, following a parameter determination procedure proposed in our previous study (Zhang et al., 2006); whereas the data on transient effects, i.e., peak stress decay (cyclic stress relaxation) and increase in specimen reference length (creep) over the cycles are used to derive parameters for the long-term viscoplastic network. This three-network model is being applied to describe the transient effects of both vocal fold cover and vocal ligament specimens.

As both tissue components are described by the same constitutive model, the approach allows for an examination of the differences in mechanical responses, such that differences between the vocal fold cover and the vocal ligament can be investigated, as well as gender-related differences. Previous studies have shown the dependence of vocal fold histological structure and vocal fold geometry on gender, e.g., in terms of collagen and elastin content, and vocal fold length (Hammond et al., 1998, 2000; Gray et al., 2000). We hypothesize that such histological and geometrical differences can be expected to be related to differences in their mechanical responses, such as stresses at different stretch levels. Possible physiological implications of the tissue transient response on phonation are also briefly discussed. We examine the hypothesis that global (Saitou et al., 2005) and local (Lieberman, 1967, 1980; Bolinger, 1968; Cooper and Sorensen, 1981; Kutik et al., 1983) changes of F₀ during phonation can be partially attributed to the transient mechanical responses of the vocal fold lamina propria.

2. Methods

2.1. Experimental measurements of tissue mechanical response

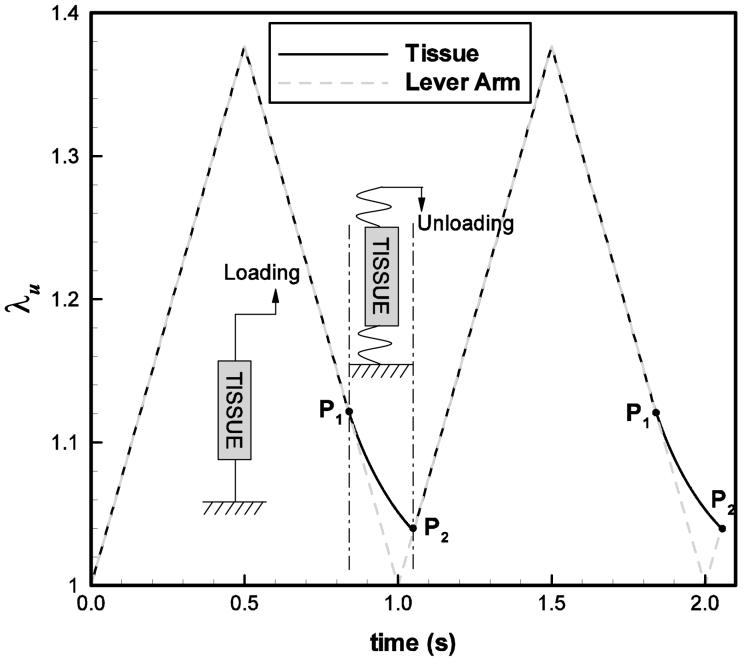
The experimental protocol for the measurement of tensile mechanical properties is briefly summarized in this section, with further details given in Chan et al. (2007). The passive uniaxial tensile stress-stretch response of the vocal fold cover and the vocal ligament was measured by sinusoidal stretch-release deformation (loading-unloading), with the use of a dual-mode servo-control lever system (Aurora Scientific Model 300BLR, Aurora, ON). Precise real-time measurements of the displacement and force of the lever arm were made by the servo-control lever system with a displacement accuracy of 1.0 μm and a force resolution of 0.3 mN. Displacement and force output of the lever system were digitized at a sampling rate of 1000 samples per second per channel with a 14-bit signal amplitude resolution (Windaq Model DI-722, DATAQ Instruments, Akron, OH). The lever system was calibrated by adjusting its electronic control circuitry under known magnitudes of displacement and force applied to the lever arm. The measured displacement and force values were then tuned so that they were within ±1% of the actual prescribed values. The servo control lever system possessed a displacement range of up to 8-9 mm in the frequency range of 1-10 Hz (Chan et al., 2007). Figure 3a illustrates the time history of the applied stretch.

Figure 3.

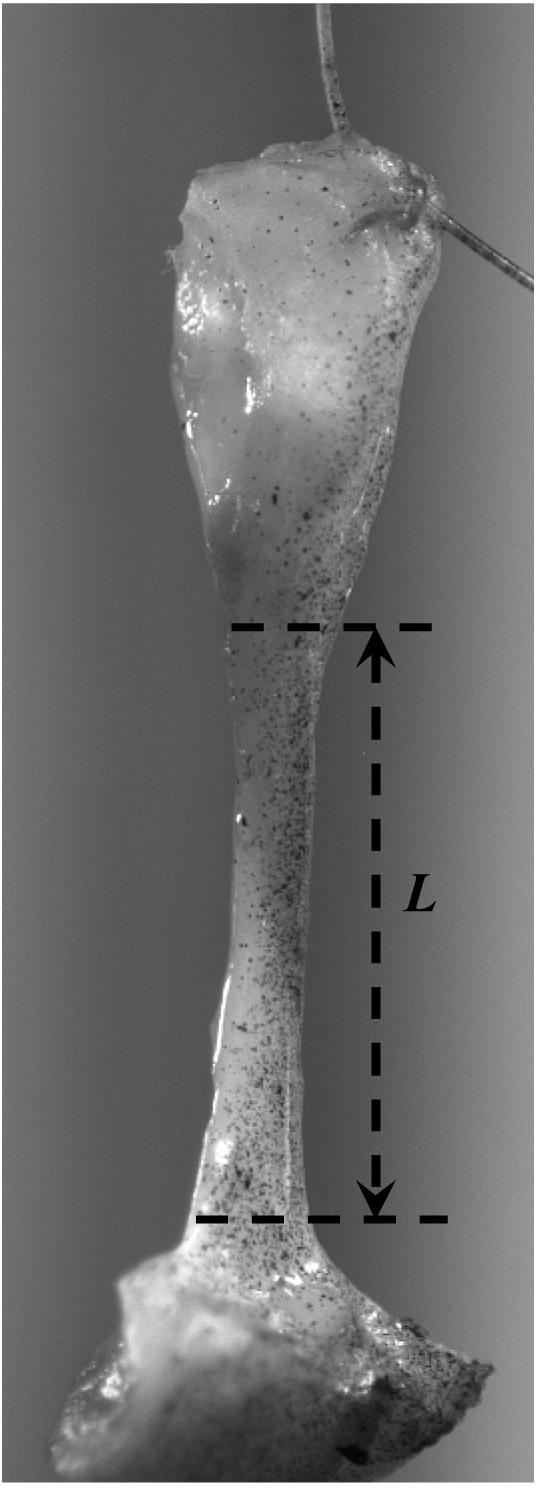
(a) A schematic representation of two load cycles. The stretch of the tissue specimen is denoted by (—) and applied displacement is represented by (- - - -). Between the points P₁ and P₂ the sutures attached to both ends of the tissue specimen are slack and no compressive load can be applied; (b) a photograph of a vocal fold ligament specimen mounted in the lever system with suture attachment through dissected sections of the thyroid cartilage (bottom) and the arytenoid cartilage (top). The initial length (mounting length) of the specimen (L) is shown.

Vocal fold cover and ligament specimens were dissected from larynges excised within 24 hours postmortem, procured from autopsy from human cadavers free of head and neck disease and laryngeal pathologies. Specimens were dissected with instruments for phonomicrosurgery, as summarized in Chan et al. (2007). All subjects were non-smokers, and were Caucasians or Hispanics, although race was not a factor in the procurement. Each specimen was mounted vertically to the lever arm of the servo-control lever system through a 3-0 suture (Ethicon, Somerville, NJ) (Fig. 3b) in Krebs-Ringer solution at pH 7.4 in an environmental chamber at 37°C. The initial length L was measured before dissection as the distance from the anterior attachment at the thyroid cartilage (i.e., the anterior commissure) to the posterior attachment at the arytenoid cartilage (i.e., the vocal process) at the most medial plane of the vocal fold (Chan et al., 2007). Specimen deformation is defined as stretch λ_u = l/L with l the displacement of the lever arm. While the deformation of the suture is negligible, the deformation of the suture insertion is most likely not. This factor was, however, not accounted for. Each specimen was stretched to a fixed maximum length l_rev at load reversal. The uniaxial stretch λ_u at load reversal is defined as λ_u,rev = l_rev/L with L being the initial length (mounting length) of the specimen. During posturing the vocal fold stretch can reach values of up to 1.5 (Hunter et al., 2004; Titze, 2006). To account for the large stretch in the physiological situation, the full displacement range of the lever system was exploited. Male specimens were loaded on average to stretch of λ_u,rev = 1.33, the female specimens were loaded on average to stretch of λ_u,rev = 1.54. Posturing typically occurs at frequencies (around 1-10 Hz) well below that of the actual vibration frequency (Hunter et al., 2004). A loading rate of 1.0 Hz was chosen in the present experiments. Up to twenty cycles of repeated loading and unloading at 1.0 Hz were performed for specimens of relevance to this study.

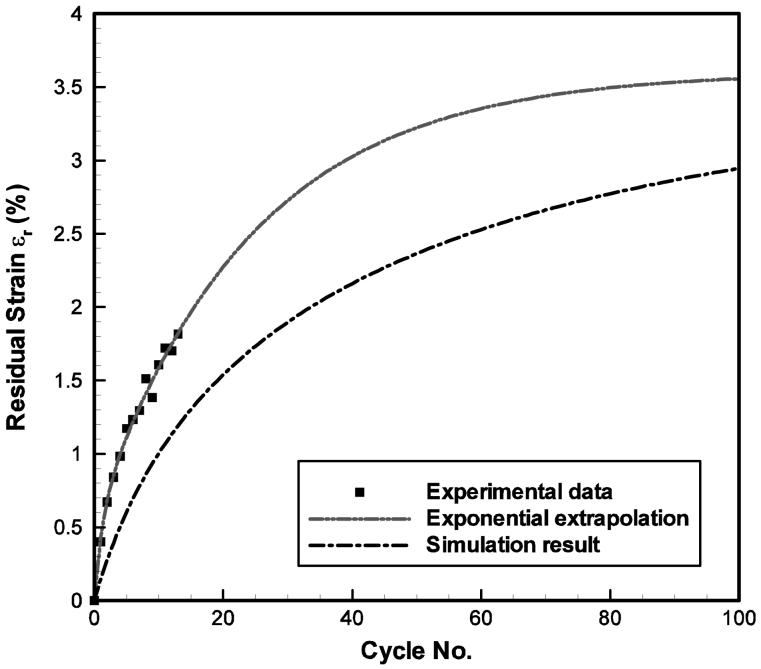
It was found that 20 load cycles indeed would not provide a stabilized mechanical response of the tissue, and that the significantly larger number of load cycles as applied to the samples of the 69-year-old male subject would be appropriate to fully characterize the transient mechanical response. Previous studies on brain tissues (Gefen and Margulies, 2004) and periodontal ligament (Komatsu et al., 2007) have shown that such transient responses can be approximated by use of exponential functions. In the present study, the peak stress values σ_p are approximated by an exponential decay function of the form,

$${\sigma }_p\left(t\right)={\sigma }_s+\sum _{k=1}^3{\sigma }_k\cdot \exp (-t∕N_k)$$ (1)

in which t is time (or cycle number), σ_s is the predicted stabilized peak stress level, and N_k (k = 1, 2, 3) are cycle constants. t = 0 is the instance at which the peak load is reached in the first cycle. Values of σ_s, σ_k and N_k (k = 1, 2, 3) are determined by fitting experimental data to the exponential function with a least-square curve-fitting process (MATLAB 7.0, The MathWorks, Natick, MA). The right-shift of the stress-stretch curves is quantified by use of the strain value at which the individual load cycle starts from zero stress. These strain values ε_r are approximated by an exponential function of the form,

$${\epsilon }_r\left(t\right)=\sum _{k=1}^3{\epsilon }_k\cdot [1-\exp (-t∕N_k)]$$ (2)

with ${\epsilon }_s={\sum }_{k=1}^3{\epsilon }_k$ the predicted stabilized residual strain level, and N_k (k = 1, 2, 3) the cycle constants, see also Eq. (1).

To test the method, for one cover specimen and one ligament specimen dissected from one vocal fold of a 69-year-old male subject, 125 cycles of repetitive tensile stretch and release at 1.0 Hz were applied to obtain high cycle number experimental information on the peak stress decay (cyclic stress relaxation) and shift of the stress-stretch curves to the right (creep). For the cover, the experimental data of σ_p and ε_r can be described by the following fit functions based on data of all 125 cycles: σ_p(cover) = 260.1+14.0·exp(-t/1.05)+25.8·exp(-t/6.34)+85.3·exp(-t/65.1) [kPa], ε_r(cover) = 1.40·[1-exp(-t/1.05)]+1.36·[1-exp(-t/6.34)]+3.49·[1-exp(-t/65.1)][%]. For the ligament only experimental values for the peak stresses could be determined, σ_p(ligament) = 82.9+5.1·exp(-t/6.09)+0.12·exp(-t/16.5)+21.4·exp(-t/85.3) [kPa]. Subsequently, we obtain an estimate of the long-term transient specimen response by determining constants σ_s, σ_k, ε_k, N_k (k = 1, 2, 3) from nonlinear fits employing only the first 15 cycles of each experiment. The experimental protocol dictated that the peak stress was measured more accurately than the stress-free lengths of the specimens. For this reason the extrapolations of the peak stress were deemed more representative than the extrapolations of the residual strain, and constants N_k are based on stress data. For the cover specimen, extrapolations based on Eqs. (1) and (2) with the first 15 cycles lead to σ_p = 283.7+22.7·exp(-t/1.70)+78.6·exp(-t/28.0)+0.003·exp(-t/948.8) [kPa] , R² = 0.997 and ε_r = 1.94·[1-exp(-t/1.70)]+3.19·[1-exp(-t/28.0)]+10.0·[1-exp(-t/948.8)][%] , R² = 0.980. For the ligament specimen, the extrapolation based on the first 15 cycles leads to σ_p = 80.9+1.7·exp(-t/1.8)+8.2·exp(-t/10.0)+22.5·exp(-t/107.7) [kPa], R² = 0.999.

The validity of the exponential extrapolation scheme was examined by comparing the estimated peak stresses and residual strains predicted employing the first 15 cycles with the experimental values observed in the 125th cycle of these specimens. For the cover, the peak stress and residual strain values recorded in the 125th cycle of the experiment are 271.5 kPa and 5.9%, respectively. The extrapolations overestimate the peak stress and the residual strain in the 125th cycle by 4.8% and 7.1%, respectively. For the ligament, the peak stress value recorded in the 125th cycle is 88.1 kPa. The extrapolation underestimates the experimental data in the peak stress observed at the 125th cycle by 0.2%. It can be seen that the predictions by the exponential fits agreed quite well with the empirical data at large cycle numbers. Consequently, the process of estimating stabilized peak stress values and residual strains by use of the exponential extrapolations is used in characterizing the long-term cyclic specimen response.

2.2. Constitutive characterization

A one-dimensional rheological representation of the three-dimensional model is given in Fig. 2. The three networks (A), (B) and (C) are in parallel with one another such that the applied deformation gradient F is identical to the deformation gradients F_i in the networks with the subscript i denoting network (A), (B) or (C):

$$\mathbf{F}={\mathbf{F}}_{\mathrm{A}}={\mathbf{F}}_{\mathrm{B}}={\mathbf{F}}_{\mathrm{C}}$$ (3)

Following this parallel arrangement of networks, the total Cauchy stress T is the sum of the Cauchy stresses in networks (A), (B) and (C), T_A, T_B, T_C:

$$\mathbf{T}={\mathbf{T}}_{\mathrm{A}}+{\mathbf{T}}_{\mathrm{B}}+{\mathbf{T}}_{\mathrm{C}}$$ (4)

The deformation gradient of the time-dependent components (B) and (C) can be decomposed multiplicatively into an elastic component F^e and a viscoplastic component F^p:

$$\mathbf{F}={\mathbf{F}}_{\mathrm{B}}={\mathbf{F}}_{\mathrm{B}}^{\mathrm{e}}\cdot {\mathbf{F}}_{\mathrm{B}}^{\mathrm{p}}={\mathbf{F}}_{\mathrm{C}}={\mathbf{F}}_{\mathrm{C}}^{\mathrm{e}}\cdot {\mathbf{F}}_{\mathrm{C}}^{\mathrm{p}}$$ (5)

The one-dimensional form of Eq. (5) in the longitudinal direction of the vocal fold can be obtained as follows,

$${\lambda }_u={\lambda }_{\mathrm{B}}^{\mathrm{e}}{\lambda }_{\mathrm{B}}^{\mathrm{p}}={\lambda }_{\mathrm{C}}^{\mathrm{e}}{\lambda }_{\mathrm{C}}^{\mathrm{p}}$$ (6)

in which λ_u is the applied stretch, ${\lambda }_i^{\mathrm{e}}$ and ${\lambda }_i^{\mathrm{p}}$ are the elastic and viscoplastic stretch components, respectively, with the subscript i denoting network (B) or (C).

The elastic response of all network components is described by the Ogden model (Zhang et al., 2006), with a shear modulus μ and a power α describing the degree of nonlinearity of the elastic response (Ogden, 1972). In this model it is assumed that the three networks (A), (B) and (C) have the same power α = α_A = α_B = α_C in the hyperelastic response, but different values of the initial network shear moduli μ_A, μ_B and μ_C. The first-order Ogden model is described by a strain energy density function w of the form,

$$w_i=\frac{2{\mu }_i}{{\alpha }^2}[{\left({\lambda }_{i,1}^{\mathrm{e}}\right)}^{\alpha }+{\left({\lambda }_{i,2}^{\mathrm{e}}\right)}^{\alpha }+{\left({\lambda }_{i,3}^{\mathrm{e}}\right)}^{\alpha }-3](i=\mathrm{A},\mathrm{B},\mathrm{C})$$ (7)

where ${\lambda }_{i,1}^{\mathrm{e}}$ is the principal stretch of the elastic component of network (A), (B) or (C) in the longitudinal direction ${\lambda }_{i,1}^{\mathrm{e}}={\lambda }_i^{\mathrm{e}}$, and ${\lambda }_{i,2}^{\mathrm{e}}$ and ${\lambda }_{i,3}^{\mathrm{e}}$ are the principal stretches in the transverse directions, which satisfy ${\lambda }_{i,1}^{\mathrm{e}}\cdot {\lambda }_{i,2}^{\mathrm{e}}\cdot {\lambda }_{i,3}^{\mathrm{e}}=1$. For uniaxial loading of a specimen of initial length L to a current length l the principal stretches in the transverse directions are ${\lambda }_{i,2}^{\mathrm{e}}={\lambda }_{i,3}^{\mathrm{e}}=1∕\sqrt{{\lambda }_i^{\mathrm{e}}}$. The stress is obtained as the derivative of the strain energy density with respect to the principal stretch in the longitudinal direction ${\lambda }_i^{\mathrm{e}}$,

$${\sigma }_i=\frac{\partial w_i}{\partial {\lambda }_i^{\mathrm{e}}}=\frac{2{\mu }_i}{\alpha }[{\left({\lambda }_i^{\mathrm{e}}\right)}^{\alpha -1}-{\left({\lambda }_i^{\mathrm{e}}\right)}^{-\frac{\alpha }{2}-1}]$$ (8)

The formulation regulating the inelastic rate of the shape change of the time-dependent components (B) and (C) follows Bergström and Boyce (1998),

$${\stackrel{`}{\mathbf{D}}}_i^{\mathrm{p}}={\dot{\stackrel{‒}{\lambda }}}_i^{\mathrm{p}}\frac{{\mathbf{S}}_i}{{\stackrel{‒}{\sigma }}_i}={\mathbf{F}}_i^{\mathrm{e}}{\stackrel{.}{\mathbf{F}}}_i^{\mathrm{p}}{\left({\mathbf{F}}_i^{\mathrm{p}}\right)}^{-1}{\left({\mathbf{F}}_i^{\mathrm{e}}\right)}^{-1}(i=\mathrm{B},\mathrm{C})$$ (9)

where S_i is the deviator of the Cauchy stress tensor in network (B) or (C), and ${\stackrel{‒}{\sigma }}_i=\sqrt{(3∕2){\mathbf{S}}_i:{\mathbf{S}}_i}$ is the corresponding effective stress in network (B) or (C). The effective inelastic stretch rate ${\dot{\stackrel{‒}{\lambda }}}_i^{\mathrm{p}}$ depends on the effective inelastic stretch ${\stackrel{‒}{\lambda }}_i^{\mathrm{p}}$ and the effective stress ${\stackrel{‒}{\sigma }}_i$:

$${\dot{\stackrel{‒}{\lambda }}}_i^{\mathrm{p}}=Z_i{({\stackrel{‒}{\lambda }}_i^{\mathrm{p}}-1+\delta )}^{c_i}{\left({\stackrel{‒}{\sigma }}_i\right)}^{m_i}$$ (10)

in which the stress exponent m_i characterizes the dependence of the inelastic deformation on the stress level in networks (B) or (C), the stretch exponent c_i (-1 ≤ c_i ≤ 0) characterizes the dependence of the rate of inelastic deformation on the current magnitude of inelastic deformation, the viscosity scaling constant Z_i defines the absolute magnitude of the inelastic deformation, and δ is a small positive number (δ < 0.001) introduced to avoid singularities in the inelastic stretch rate when the inelastic stretch is close to unity (Bergström and Boyce, 2001). The inelastic component of the deformation gradient in network (B) or (C) is obtained by inverting the relationships presented in Eq. (9) and then substituting into Eq. (10),

$$\begin{array}{cc}\hfill {\stackrel{.}{\lambda }}_i^{\mathrm{p}}=& \frac{2}{3}{\lambda }_i^{\mathrm{p}}\cdot Z_i\cdot \mathrm{sgn}({\lambda }_i^{\mathrm{e}}-1)\cdot {\left\{\sqrt{\frac{1}{3}\left[{\left({\lambda }_i^{\mathrm{p}}\right)}^2+\frac{2}{{\lambda }_i^{\mathrm{p}}}\right]}-1+\delta \right\}}^{c_i}\hfill \\ \hfill & \cdot {\mid \frac{2{\mu }_i}{\alpha }\left[{\left({\lambda }_i^{\mathrm{e}}\right)}^{\alpha }-{\left({\lambda }_i^{\mathrm{e}}\right)}^{-\frac{\alpha }{2}}\right]\mid }^{m_i}(i=\mathrm{B},\mathrm{C})\hfill \end{array}$$ (11)

Under consideration of the time-dependent response, stress is calculated from the elastic components of stretch ${\lambda }_{\mathrm{A}}^{\mathrm{e}}$, ${\lambda }_{\mathrm{B}}^{\mathrm{e}}$ and ${\lambda }_{\mathrm{C}}^{\mathrm{e}}$, all of which depend on the applied stretch λ_u and the applied stretch rate ${\stackrel{.}{\lambda }}_u$. For network (A) the elastic stretch rate is ${\stackrel{.}{\lambda }}_{\mathrm{A}}^{\mathrm{e}}={\stackrel{.}{\lambda }}_{\mathrm{A}}={\stackrel{.}{\lambda }}_u$ and the elastic stretch is ${\lambda }_u={\lambda }_{\mathrm{A}}={\lambda }_{\mathrm{A}}^{\mathrm{e}}$. In networks (B) and (C) the elastic stretch rate ${\stackrel{.}{\lambda }}_{\mathrm{B}}^{\mathrm{e}}$ and ${\stackrel{.}{\lambda }}_{\mathrm{C}}^{\mathrm{e}}$ can be expressed as follows when substituting Eq. (6) into Eq. (11),

$$\begin{array}{cc}\hfill {\stackrel{.}{\lambda }}_i^{\mathrm{e}}& ={\stackrel{.}{\lambda }}_u\frac{{\lambda }_i^{\mathrm{e}}}{{\lambda }_u}-\frac{2}{3}{\lambda }_i^{\mathrm{e}}\cdot Z_i\cdot \mathrm{sgn}({\lambda }_i^{\mathrm{e}}-1)\cdot {\left\{\sqrt{\frac{1}{3}\left[{\left(\frac{{\lambda }_u}{{\lambda }_i^{\mathrm{e}}}\right)}^2+\frac{2{\lambda }_i^{\mathrm{e}}}{{\lambda }_u}\right]}-1+\delta \right\}}^{c_i}\hfill \\ \hfill & \cdot {\mid \frac{2{\mu }_i}{\alpha }\left[{\left({\lambda }_i^{\mathrm{e}}\right)}^{\alpha }-{\left({\lambda }_i^{\mathrm{e}}\right)}^{-\frac{\alpha }{2}}\right]\mid }^{m_i}(i=\mathrm{B},\mathrm{C})\hfill \end{array}$$ (12)

During loading and at the beginning of unloading, the applied stretch rate is prescribed by the lever arm as constant, ${\stackrel{.}{\lambda }}_u=\mathit{const}$. (Fig. 3a). Then, the elastic stretch component ${\lambda }_{\mathrm{B}}^{\mathrm{e}}$ and ${\lambda }_{\mathrm{C}}^{\mathrm{e}}$ can be found through numerical integration of Eq. (12) (MATLAB 7.0, The MathWorks, Natick, MA). With these formulations, the total nominal stress σ can be obtained from Eq. (8):

$$\sigma =\frac{2{\mu }_{\mathrm{A}}}{\alpha }\left[{\lambda }_u^{\alpha -1}-{\lambda }_u^{-\frac{\alpha }{2}-1}\right]+\frac{2{\mu }_{\mathrm{B}}}{\alpha }\left[{\left({\lambda }_{\mathrm{B}}^{\mathrm{e}}\right)}^{\alpha -1}-{\left({\lambda }_{\mathrm{B}}^{\mathrm{e}}\right)}^{-\frac{\alpha }{2}-1}\right]+\frac{2{\mu }_{\mathrm{C}}}{\alpha }\left[{\left({\lambda }_{\mathrm{C}}^{\mathrm{e}}\right)}^{\alpha -1}-{\left({\lambda }_{\mathrm{C}}^{\mathrm{e}}\right)}^{-\frac{\alpha }{2}-1}\right]$$ (13)

During cyclic loading, the reference length of the specimen was observed to increase. Since in the experimental protocol loading is displacement controlled, toward the end of unloading of each cycle the sutures attached to both ends of the tissue specimen are slack due to the creep behavior. The sutures thus apply no load on the specimen (Fig. 3a). During this special “relaxation” period, the total stress σ remains zero and the overall stretch rate ${\stackrel{.}{\lambda }}_u$ is unknown. The governing equation is that the time derivative of the stress [Eq. (13)] remains zero,

$$\begin{array}{cc}\hfill \frac{d\sigma }{dt}=& \frac{\partial \sigma }{\partial {\lambda }_u}{\stackrel{.}{\lambda }}_u+\frac{\partial \sigma }{\partial {\lambda }_{\mathrm{B}}^{\mathrm{e}}}{\stackrel{.}{\lambda }}_{\mathrm{B}}^{\mathrm{e}}+\frac{\partial \sigma }{\partial {\lambda }_{\mathrm{C}}^{\mathrm{e}}}{\stackrel{.}{\lambda }}_{\mathrm{C}}^{\mathrm{e}}\hfill \\ \hfill =& \sum _{i=\mathrm{A},\mathrm{B},\mathrm{C}}\frac{2{\mu }_i}{\alpha }\left[(\alpha -1){\left({\lambda }_i^{\mathrm{e}}\right)}^{\alpha -2}+\left(\frac{\alpha }{2}+1\right){\left({\lambda }_i^{\mathrm{e}}\right)}^{-\frac{\alpha }{2}-2}\right]\cdot {\stackrel{.}{\lambda }}_i^{\mathrm{e}}=0\hfill \end{array}$$ (14)

in which ${\lambda }_{\mathrm{A}}^{\mathrm{e}}={\lambda }_{\mathrm{A}}={\lambda }_u$ is the overall stretch, ${\lambda }_{\mathrm{B}}^{\mathrm{e}}$ and ${\lambda }_{\mathrm{C}}^{\mathrm{e}}$ are the elastic stretch components of networks (B) and (C), respectively. From Eqs. (12) and (14), all the stretch components can be calculated numerically. During unloading, when the total stress σ vanishes, it serves as an indicator to replace the condition ${\stackrel{.}{\lambda }}_u=\mathit{const}$. with Eq. (14) in the numerical integration process (point P₁ in Fig. 3a); during the relaxation period, when the lever arm displacement (dashed line in Fig. 3a) catches up with the real stretch of the tissue specimen (solid line in Fig. 3a), the numerical integration process will be switched back into Eq. (12) (point P₂ in Fig. 3a) together with the constant applied stretch rate condition.

The Appendix describes the optimization procedure to determine the values of the constitutive parameters. The constitutive parameters are uniquely determined for each specimen and thus characterize the empirical mechanical response of that individual specimen.

3. Results

Tissue specimens were obtained from six male subjects of ages Y(male) = 33, 51, 65, 66, 88 and 99 years and six female subjects of ages Y(female) = 73, 80, 82A, 82B, 83 and 84 years. Table 1 shows the characteristics of the subjects and the specimens. The extrapolation of the peak stress was deemed more representative than extrapolation of the residual strain and hence the determination of the constitutive parameters was based on stress data primarily. Shown in Table 1 are the experimental data for the peak stresses of the first cycle, the experimental data for the peak stresses and the residual strains of the 10th cycle (a representation of the transient response), the stabilized peak stresses and residual strains predicted (extrapolated) by exponential fits, and the simulation results. For several specimens no residual strain was detected in the experiment. The relative differences between peak stress values from the simulation, Eqs. (13), and the experimental data (or their exponential extrapolations in the case of the stabilized response) are smaller than 3% for all specimens. The results of the simulated creep behavior are less satisfactory for some of the specimens.

Table 1.

Summary of the vocal fold in situ lengths and comparisons between experimental data (Exp.), extrapolated (predicted) responses based on exponential fits (Pre.), and simulation results based on constitutive modeling (Sim.) for all specimens; σ_p,1 -peak stress of the 1st cycle; σ_p,10 - peak stress of the 10th cycle; ε_r,10 - residual strain after 10 cycles of repeated loading-unloading; σ_s - peak stress of the stabilized response; ε_s - residual strain of the stabilized response; (c) - vocal fold cover; (l) -vocal ligament

Gender	Age	L	λu,rev	σp,1 [kPa]		σp,10 [kPa]		σs [kPa]		εr,10 (%)		εs (%)
		[mm]	[-]	Exp.	Sim.	Exp.	Sim.	Pre.	Sim.	Exp.	Sim.	Pre.	Sim.
Male	33 (c)	17.9	1.33	21.1	21.1	19.6	19.7	17.4	17.4	1.18	0.74	7.44	3.36
	33 (l)	17.9	1.32	29.6	29.5	28.5	28.5	24.4	24.4	1.29	0.29	7.78	2.71
	51 (c)	21.4	1.38	17.0	17.0	16.4	16.3	14.5	14.6	1.75	0.42	4.99	2.94
	51 (l)	21.4	1.39	22.0	22.0	21.2	21.2	19.9	19.9	1.39	0.34	2.20	2.04
	65 (c)	20.5	1.27	27.7	27.7	25.4	25.0	21.8	21.8	1.61	1.01	3.60	3.44
	65 (l)	20.5	1.23	38.6	38.7	37.8	37.3	22.0	22.0	0.34	0.17	4.87	3.79
	66 (c)	20.4	1.40	72.4	72.4	56.0	55.7	41.1	41.1	3.64	4.43	4.92	10.65
	66 (l)	20.4	1.31	59.6	59.6	56.1	56.1	52.5	52.5	0.65	0.46	1.30	2.14
	88 (l)	20.7	1.37	86.0	86.0	76.5	76.1	70.8	70.8	0	1.39	-	3.99
	99 (c)	17.9	1.30	29.5	29.5	28.4	28.1	10.1	10.1	1.38	0.49	5.20	11.27
	99 (l)	17.9	1.33	63.5	63.5	36.3	36.3	18.8	18.8	3.01	3.88	6.21	10.54
Female	73 (c)	16.9	1.54	56.7	56.7	50.9	51.8	28.9	29.0	0	6.07	-	13.84
	73 (l)	16.9	1.47	18.5	18.5	17.6	17.7	8.82	8.83	0	0.44	-	8.21
	80 (c)	14.5	1.50	108.3	108.4	100.3	100.8	79.9	80.1	1.62	0.71	3.56	5.66
	80 (l)	14.5	1.51	67.2	67.2	58.3	57.2	28.3	28.3	0.85	1.36	10.9	10.74
	82A (c)	14.9	1.48	120.6	120.6	113.1	112.9	97.3	97.3	1.32	0.64	9.30	4.62
	82A (l)	14.9	1.47	147.0	147.0	138.6	139.8	103.2	103.4	2.38	0.50	17.7	6.20
	82B (c)	14.6	1.55	107.1	107.1	98.7	97.3	94.1	94.1	0	8.45	-	9.49
	82B (l)	14.6	1.59	57.3	57.3	47.0	46.8	40.5	40.5	0	9.42	-	13.16
	83 (c)	15.1	1.49	130.9	131.0	127.9	128.0	120.3	120.4	0	1.36	-	3.07
	83 (l)	15.1	1.57	61.7	61.7	58.2	57.9	48.6	48.6	0.97	3.49	12.9	6.60
	84 (l)	11.1	1.74	135.0	135.0	129.2	126.6	79.4	79.4	0	8.61	-	17.75

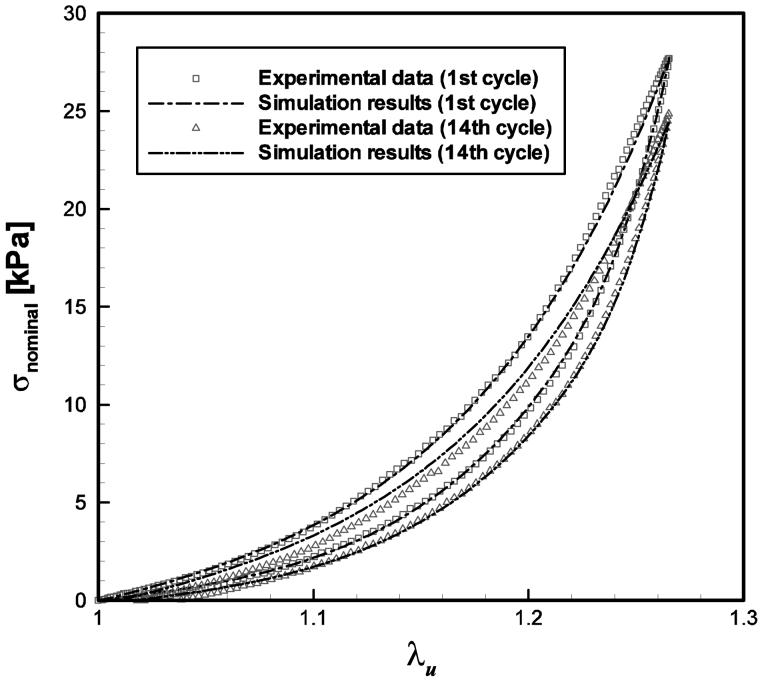
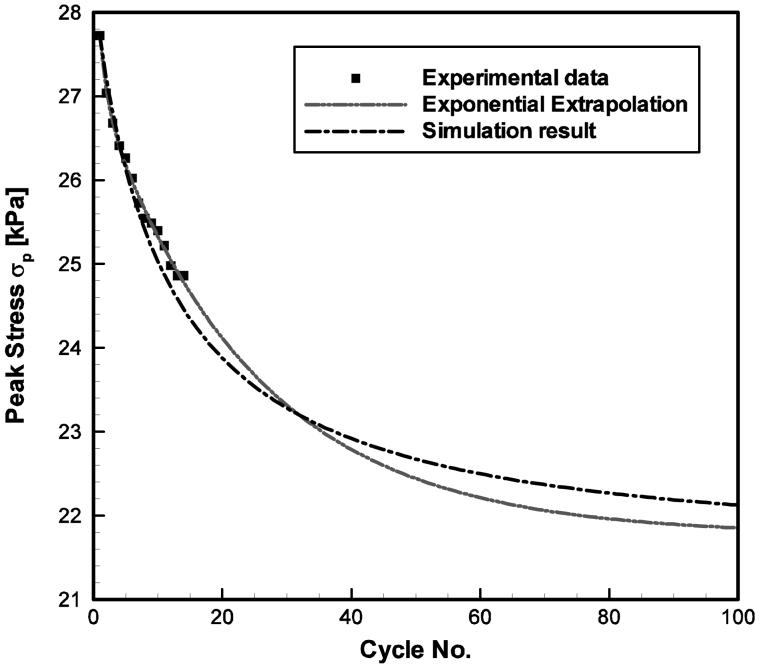
Parameter values for all specimens are summarized in Table 2. Figure 4 shows the typical simulation results of the constitutive model in comparison to the experimental data, as illustrated for the 65-year-old male vocal fold cover. Stress-stretch curves obtained from other specimens showed similar characteristics in the comparison between data and simulation results, but with significant inter-specimen variability in the data. A strong nonlinear dependence of stress on the applied stretch is observed, especially at higher stretch (λ_u ≥ 1.2). This finding is similar to previous data of both the human vocal ligament and the vocal fold cover (Min et al., 1995; Zhang et al., 2006; Chan et al., 2007). Figure 4a demonstrates the comparison between constitutive model simulations and experimental results for the first and the 14th cycles in cyclic loading-unloading. For most of the specimens, a notable peak stress decay (cyclic stress relaxation) and shift of the stress-stretch curves to the right (creep) were observed experimentally, as summarized in Table 1. Figure 4b exhibits the peak stress decay over the cycles of loading-unloading; Fig. 4c displays the residual strain in dependence of the number of cycles. It can be seen from Fig. 4 that the nonlinearity and the hysteresis of the stress-stretch curves, as well as the transient effects of stress relaxation and creep can be characterized very well by the three-network constitutive model.

Table 2.

Summary of the constitutive model parameters of all specimens; μ_i - initial shear modulus; α - power in Ogden model; Z_i - viscoplastic scaling constant; m_i -stress exponent (subscript i denoting network (A), (B) or (C)); (c) - vocal fold cover; (l) - vocal ligament

Gender	Age	μA	μB	μC	α	ZB	mB	ZC	mC
		[kPa]	[kPa]	[kPa]		[s-1(kPa)-mB]		[s-1(kPa)-mc]
Male	33 (c)	2.82	20.0	0.74	13.8	0.05	1.8	0.005	1.0
	33 (l)	3.33	50.0	0.87	15.3	0.02	1.4	0.001	1.2
	51 (c)	1.38	40.0	0.28	14.3	0.06	1.5	0.005	1.2
	51 (l)	1.33	50.0	0.16	15.2	0.04	1.3	0.01	1.3
	65 (c)	5.02	60.0	1.87	15.3	0.005	1.6	0.003	1.1
	65 (l)	1.83	40.0	1.99	24.0	0.006	1.5	0.00008	1.1
	66 (c)	2.30	130.0	2.35	15.0	0.0025	1.8	0.001	1.1
	66 (l)	2.76	50.0	0.44	20.0	0.004	1.3	0.004	1.0
	88 (l)	3.70	130.0	1.05	16.9	0.0045	1.2	0.002	1.4
	99 (c)	1.13	40.0	5.14	14.0	0.01	2.1	0.0001	1.0
	99 (l)	0.57	40.0	2.04	20.2	0.01	1.2	0.0008	1.1
Female	73 (c)	0.26	70.0	0.36	16.2	0.02	1.3	0.0002	1.1
	73 (l)	0.20	60.0	0.45	14.7	0.05	1.1	0.0001	1.5
	80 (c)	2.17	190.0	0.97	14.3	0.008	1.1	0.00015	1.4
	80 (l)	0.40	65.0	0.87	15.5	0.02	1.2	0.00002	1.8
	82A (c)	2.50	70.0	0.68	15.4	0.01	1.7	0.0006	1.1
	82A (l)	5.91	50.0	3.05	13.0	0.005	1.5	0.00008	1.2
	82B (c)	0.37	40.0	0.065	18.8	0.02	1.3	0.009	1.1
	82B (l)	0.43	80.0	0.23	14.9	0.02	1.3	0.003	1.2
	83 (c)	1.09	150.0	0.11	18.2	0.008	1.0	0.0005	1.5
	83 (l)	0.14	50.0	0.041	19.0	0.08	1.2	0.001	1.1
	84 (l)	1.17	80.0	1.08	11.4	0.006	1.7	0.00006	1.2

Figure 4.

Comparisons between the predictions (extrapolations) by the exponential fits (the dash-dot-dot lines) with the experimental data (the symbols) and the constitutive model simulation results (the dash-dot lines) of the tensile stress-stretch response of the 65-year-old male vocal fold cover specimen at 1.0 Hz: (a) the first and the 14th cycles of the stress-stretch responses; (b) the peak stress decay over cycles and (c) the evolution of the reference length over cycles.

Further analysis of the data involved comparing the vocal fold cover and the vocal ligament to each other. In order to conduct paired statistical tests and to make this comparison meaningful, only those subjects with both cover and ligament specimens available are selected for the analysis, including five male (Y=33, 51, 65, 66, 99 years) and five female subjects (Y=73, 80, 82A, 82B, 83 years). The constitutive model was utilized to predict the mechanical response for each specimen under two ramp stretch histories at a stretch rate of 0.4/sec, but at two different stretch levels that are typical of phonation (1.2 and 1.4) (Hollien, 1960). The value of stretch rate 0.4/sec was considered since it represents a lower bound for all experiments of the present study. The peak stresses at the end of loading were compared to investigate any differences between the cover and the ligament. Detailed results of the statistical tests on comparisons between the cover and the ligament are given in Table 3. For paired Wilcoxon signed-rank tests, only the differences between the cover and the ligament of the same subject are of concern. Based on procedures following the paired Wilcoxon signed-rank tests the data did not reflect any significant difference between the cover and the ligament except for the peak stress at a stretch of 1.4 for males.

Table 3.

Summary of the results of statistical tests conducted on the peak stresses at different stretch levels and characteristic time constants (comparisons between the vocal fold cover and the vocal ligament)

Gender	Parameter	Cover			Ligament			Paired tests?	p-value
		mean	SD	n	mean	SD	n
Male	σ(λu = 1.2) [KPa]	8.32	4.12	5	10.78	7.14	5	Yes	0.09
	σ(λu = 1.4) [kPa]	60.92	32.85		217.7	266.5			0.03
	τB (ms)	122.9	72.3		76.6	49.9			0.31
	τC (s)	248.2	190.2		266.8	148.3			0.5
Female	σ(λu = 1.2) [kPa]	3.97	2.27	5	3.90	5.27	5	Yes	0.31
	σ(λu = 1.4) [kPa]	34.92	17.56		26.32	30.80			0.22
	τB (ms)	35.4	25.8		37.9	50.2			0.5
	τC (s)	1452	1116		2859	2416			0.16

The dependence of the mechanical response on gender is investigated for the cover and the ligament separately. For the vocal fold cover specimens we found a male-to-female difference of ${\stackrel{‒}{\sigma }}_c\left(\text{male}\right){\mid }_{{\lambda }_u=1.2}-{\stackrel{‒}{\sigma }}_c\left(\text{female}\right){\mid }_{{\lambda }_u=1.2}=4.35\mathrm{kPa}$ in the mean value of the peak stress at a stretch of 1.2. A Wilcoxon rank-sum test indicates this difference to be statistically not significant (p = 0.08). A similar analysis of gender-related difference was also conducted for the peak stress at a stretch of 1.4. The data from the simulations by the constitutive model result in a difference between male and female of ${\stackrel{‒}{\sigma }}_c\left(\text{male}\right){\mid }_{{\lambda }_u=1.4}-{\stackrel{‒}{\sigma }}_c\left(\text{female}\right){\mid }_{{\lambda }_u=1.4}=26.0\mathrm{kPa}$. The result of a Wilcoxon rank-sum test indicates that this difference is statistically not significant with p = 0.11. Detailed results of the statistical tests on gender differences are listed in Table 4. For the vocal ligament specimens, a male-to-female difference in the mean values of peak stresses at a stretch of 1.2 of ${\stackrel{‒}{\sigma }}_l\left(\text{male}\right){\mid }_{{\lambda }_u=1.2}-{\stackrel{‒}{\sigma }}_l\left(\text{female}\right){\mid }_{{\lambda }_u=1.2}=7.07\mathrm{kPa}$ was found. A Wilcoxon rank-sum test indicates that this gender-related difference in peak stress at a stretch of 1.2 was statistically significant (p = 0.03). For the peak stress at a stretch of 1.4, a difference between male and female of ${\stackrel{‒}{\sigma }}_l\left(\text{male}\right){\mid }_{{\lambda }_u=1.4}-{\stackrel{‒}{\sigma }}_l\left(\text{female}\right){\mid }_{{\lambda }_u=1.4}=176.1\mathrm{kPa}$ was found. The result of a Wilcoxon rank-sum test indicates that the difference was statistically significant with p = 0.004 (Table 4).

Table 4.

Summary of the results of statistical tests conducted on the peak stresses at different stretch levels and characteristic time constants (differences across gender)

Component	Parameter	Male			Female			Paired tests?	p-value
		mean	SD	n	mean	SD	n
Cover	σ(λu = 1.2) [KPa]	8.32	4.12	5	3.97	2.27	5	No	0.08
	σ(λu = 1.4) [kPa]	60.92	32.85		34.92	17,56			0.11
	τB (ms)	122.9	72.3		35.4	25.8			0.02
	τC (s)	248.2	190.2		1452	1116			0.008
Ligament	σ(λu = 1.2) [kPa]	10.94	6.39	6	3.87	4.72	5	No	0.03
	σ(λu = 1.4) [kPa]	200.6	242.0		24.48	27.92			0.004
	τB (ms)	70.3	47.2		46.8	49.9			0.15
	τC (s)	252.9	136.9		3062	2217			0.001

In order to quantify the time-dependent response, characteristic time constants τ_i (i = B, C) are defined for each viscoplastic network as the time required for 90% stress relaxation to have occurred at a stretch of 1.2 in the respective network. Networks (B) and (C) are characterized by stretch exponents c_B = -1.0 and c_C = 0.0, respectively, and thus contribute differently to the relaxation response. The values of the two time constants were calculated for each specimen under consideration. It was found that the time constant of the short-term response provided by network (B) is on the order of 10 ms, whereas the time constant of network (C) is on the order of 100 s. Statistical tests (Wilcoxon test) were conducted for the two time constants to investigate differences between the cover and the ligament, and gender-related differences. As in the comparisons of peak stresses, only those subjects with both cover and ligament specimens available were selected for cover-ligament comparison. Detailed results of the statistical tests are shown in Table 3 and 4. Statistically significant gender difference was found in τ_B and τ_C of the cover and τ_C of the ligament. In general, τ_B for males is larger than that for females, while τ_C for males is smaller than that for females. It can be seen that the time constants of the cover are in general comparable to those of the ligament for both genders (no statistically significant difference), which might be a representation of synergy between the two tissue components.

4. Discussion

It is well known that cyclic loading influences the mechanical properties of soft tissues (Fung, 1993). What can be observed directly from the cyclic tensile stress-stretch curves of the vocal fold lamina propria in this study are a decrease of peak stress and the shift of stress-stretch curves to the right over the cycles of tensile deformation. While it was previously argued that approximately 20 cycles would be sufficient to stabilize vocal fold tissue specimens, we find indication that a significantly larger number of load cycles is needed. In order to accommodate this finding with a specimen population that was tested on a small cycle number only, an extrapolation scheme was devised and tested on independent experiments. The observed transient mechanical responses during cyclic loading are in principle similar to those observed for other soft tissues (Woo et al., 1981; Woo, 1982; Hubbard and Chun, 1988; Schatzmann et al., 1998; Yamamoto et al., 1999; Carew et al., 2000; Sverdlik and Lanir, 2002; Giles et al., 2007). Experimental studies on vocal fold tissue are however difficult in that only two specimens per subject can be obtained. This certainly limits the ability to conduct experiments considering wide arrays of stretch and stretch rate conditions. It has been argued that these features occur because the internal structure of the tissue changes with the cyclic deformation (Fung, 1993). From a structural point of view, the extracellular matrix (ECM) of the human vocal fold lamina propria is composed of fibrous proteins and interstitial proteins (Gray et al., 2000), with the fibrous proteins (collagen and elastin) presumed to carry most of the tensile stress, whereas the interstitial proteins (proteoglycans and structural glycoproteins, such as hyaluronic acid) serve as crosslinks between collagen and elastin, regulating the viscoelastic properties of the ECM (Chan et al., 2007). It is speculated that the transient effects observed in the cyclic loading of the vocal fold lamina propria could result from the unraveling of some of those crosslinks between the proteins. For the same reason, the hysteresis loop, an important indicator of the energy dissipation in the tissue, decreases with increase in the number of loading cycles.

Results of the present study show that more than 100 cycles of loading are required to stabilize the vocal fold tissue specimens. Previous studies have reported a wide range of the number of cycles needed for stabilization - between 3 and 200 cycles of loading - depending on the tissue type and the mechanical tests conducted. Schatzmann et al. (1998) found that more than 150 cycles are required to achieve a stabilized state with no further creep for human quadriceps tendons and patellar ligaments; while Woo (1982) and Yamamoto et al. (1999) stated that after 10-20 cycles the stress decay during consecutive cycles reached a steady response for rabbit patellar tendon, swine digital extensor, and flexor tendons and medial collateral ligament (MCL) of both swine and dog. For the examined vocal fold tissue specimens, the peak stress on average dropped by 30.9% (SD ± 18.9%) from the first cycle to the stabilized response. Meanwhile, the reference lengths of the vocal fold specimens increased by 4.7% (SD ± 4.8%) from the first cycle to the stabilized response. All these findings are comparable to those of published studies on other soft tissues. Woo et al. (1981) observed that peak stress decreased by around 16% for canine MCL after 10 preconditioning cycles. Peak stress decay ranging from 6% to 14% was recorded for canine limb tendons by Hubbard and Chun (1988) after the first 12 seconds of cyclic extension. Schatzmann et al. (1998) observed an average increase in the reference length of 2.2% for the quadriceps tendons and 3.2% for the patellar ligaments. Sverdlik and Lanir (2002) also recorded an increase of the stress-free length from 1.33% to 3.48% for sheep digital tendons, depending upon the level of strain applied.

It has been recognized that the vocal fold lamina propria may not be completely isotropic with a primarily parallel arrangement of collagen and elastin fibers, particularly for the vocal ligament (Chan and Titze, 1999; Alipour et al., 2000). In the present study, however, effects of anisotropy are not considered and only the tissue response in the anterior-posterior direction is investigated. It is the tissue response in that direction that is of concern in most structural models of human phonation F₀ regulation (Titze, 1994; Titze and Hunter, 2004). As all specimens are characterized with a single constitutive framework, comparisons of mechanical response across gender and between the cover and the ligament can be made. Testing of human tissue specimens invariably leads to variations in testing conditions due to specimen geometry variations thus making statistical comparison based on raw stress-stretch data impossible. This problem can be circumvented if the constitutive framework is used to construct stress-stretch curves under identical conditions for all specimens. Results of statistical tests showed that for male the peak stress in the ligament is significantly higher than that in the cover at a higher stretch level (λ_u = 1.4). This finding implies that when subjected to a higher stretch the ligament would be capable of carrying a larger tensile stress. This finding is in agreement with the body-cover model (Titze, 1994), which states that when both the cover and the ligament are in vibration, the vocalis muscle can stiffen the body of the vocal fold (including part of the ligament) while slackening the cover. Interestingly, this may not apply for female, as no statistically significant differences in the peak stresses were found between the vocal fold cover and the vocal ligament at two different stretch levels. Indeed, Chan et al. (2007) found that for female the vocal fold cover has a slightly higher mean elastic modulus (Young’s modulus) than the vocal ligament.

As for the gender dependence of the mechanical responses, statistically significant differences were found in the peak stresses at two stretch levels (1.2 and 1.4) between the male ligament and the female ligament (Table 4), while the p-values for comparisons between the male cover and the female cover are also very close to 0.05. These results suggested that male vocal folds are generally stiffer than female vocal folds, in agreement with previous findings that male vocal folds generally have higher concentration of collagen than female vocal folds (Hammond et al., 2000). Higher stress in the male vocal fold on average apparently could lead to a higher fundamental frequency (F₀) than the average female. However, since female vocal folds are usually much shorter than male, and also as female vocal folds are subjected to a higher stretch level during speaking than male (Hollien, 1960), they may both compensate for a lower elastic modulus or a lower degree of nonlinearity, contributing to a higher overall F₀ for the female voice. These findings on statistical differences have to be considered as preliminary due to the small number of samples in our experiments, as well as the relatively large inter-subject variability observed.

The observed transient effects of the vocal fold lamina propria might have important physiological implications on phonation, when the vocal fold oscillates at a high frequency and the tensile stretch applied on the vocal fold becomes repetitive, similar to the situation of cyclic loading-unloading. The time constants emerging from the model could be considered to correspond to the time constants observed in phonation. The fundamental period of vocal fold vibration (1/F₀) is on the order of 1-10 ms, shorter than the short-term time constant τ_B, while a fraction of an utterance is usually on the order of 100-5000 ms, shorter than the long-term time constant τ_C. These relative values of the time constants may contribute to the fact that self-sustained oscillation of the vocal fold does occur during the production of utterances. The cyclic stress relaxation could affect the fundamental frequency by gradually lowering the tensile stress in the tissue. A widely observed and interesting phenomenon about global changes of F₀ is that F₀ tends to fall gradually during the course of a declarative sentence (Lieberman, 1967, 1980; Bolinger, 1968; Cooper and Sorensen, 1981; Kutik et al., 1983). It is hypothesized that cyclic stress relaxation of the vocal fold lamina propria as characterized by the three-network model could account for a significant portion of the F₀ declination, whereas the short-term response provided by the viscoplastic network (B) could capture local changes of F₀, such as undershoot and overshoot (Saitou et al., 2005). It can be seen from the present data (Table 4) that the time constant τ_B of the average male is larger than that of the average female, and the time constant τ_C of the average male is significantly smaller than that of the average female. This seems to imply that local changes of F₀ would occur more quickly for the average female than the average male, yet a more prolonged overall F₀ declination may be observed in the average female. Further studies on F₀ predictions at the sentence level are currently ongoing, with some preliminary results reported in Zhang et al. (2008).

Further improvements can be made in the experimental measurements of the tissue mechanical response. In the present set of experiments, the sutures are attached to the cartilages at both ends of the tissue specimen. During cyclic loading, there will be some elongation in the sutures and the cartilages, especially in the latter. The stretch of the sutures and the cartilages is much lower than that of the specimen, as the vocal fold tissue is much more compliant. Nonetheless, the real stretch applied on the specimen is somehow overestimated. Optical strain measurements would allow one to eliminate this influence.

5. Conclusion

The transient mechanical responses of the vocal fold lamina propria are very important and interesting phenomena, but not many data have been reported previously. Based on the two-network model in our previous study (Zhang et al., 2006), a three-network constitutive model is proposed to account for the transient responses of the vocal fold lamina propria, specifically the cyclic stress relaxation and creep behavior under tensile deformation. The model is composed of an equilibrium hyperelastic network based on the Ogden’s model in parallel with two viscoplastic networks, such that one offers the short-term viscous response and the other the long-term viscous response. It is shown that the three-network model can capture the transient phenomena of cyclic stress relaxation and creep reasonably well. As similar mechanical behaviors have been observed in other biological soft tissues, the constitutive model proposed in the present study, though developed for the vocal fold lamina propria, could have applications in other soft tissues. Constitutive model parameters were determined from the experimental tensile stress-stretch data of a set of human vocal fold cover and vocal ligament specimens. Particular attention was given to the state at unload-load reversal, where loading shifts from displacement control to relaxation under zero applied stress. The three-network model captures this load state since residual stresses developed in its individual networks branch. Future work would aim to apply the constitutive model to complex stretch histories. Such studies would prove if the constitutive model can be successful beyond its use in tissue characterization as successfully conducted in this study. Comparisons were conducted between the cover and the ligament specimens and also between male and female. It was found that for male the peak stress in the vocal ligament was significantly higher than that in the vocal fold cover under a relatively high level of stretch (λ_u = 1.4). Female vocal folds in general are found to be more compliant than male vocal folds, with the peak stress in the male vocal ligament significantly higher than that in the female vocal ligament at both stretch levels (1.2 and 1.4). However, the size of our empirical data pool was limited and our conclusions should be considered as preliminary. The proposed three-network model could provide a useful tool for predicting the fundamental frequency (F₀) of phonation when combined with the ideal string model (Titze, 1994; Zhang et al., 2006) or the composite beam model (Titze and Hunter, 2004; Zhang et al., 2007).

Appendix

The procedure followed in the parameter identification is based on our previous study (Zhang et al., 2006) after Bergström and Boyce (2001), but incorporates modifications appropriate for the current choice of the hyperelastic response.

First the parameters of networks (A) and (B) are determined by the first stress-stretch cycle of cyclic loading-unloading of the specimen. The values of μ_A and α are determined through a least-square optimization process following the Levenberg-Marquardt method to best fit the experimental equilibrium response estimated from the empirical stress-stretch curves as the midpoint values of equal stretch between the loading and unloading portions of the hysteresis loop. Subsequently, the initial shear modulus of network (B) can be determined from the tangent stiffness E_t at load reversal of the first stress-stretch cycle. At the instant of load reversal, network (B) responds through its hyperelastic deformation only. Thus the tangent modulus at the onset of unloading E_t is the sum of the elastic moduli of the two networks:

$$E_t=3{\mu }_{\mathrm{B}}+\frac{2{\mu }_{\mathrm{A}}}{\alpha }\left[(\alpha -1){\lambda }_{u,\mathrm{rev}}^{\alpha -2}+\left(\frac{\alpha }{2}+1\right){\lambda }_{u,\mathrm{rev}}^{-\frac{\alpha }{2}-2}\right]$$ (A.1)

The viscosity scaling constant Z_B is then obtained such that the simulated loading-unloading curves expand gradually from the equilibrium curve to fit the experimental data points of the stress-stretch hysteresis loop. The stress power parameter m_B is chosen such that the predicted response fits the initial slope of the experimental loading curves. For all the specimens of the present investigation the stretch power parameter is set to c_B = -1.0. With this choice the model allows the network (B) to relax quickly and to provide the short-term viscous behaviors.

Network (C) is supposed to provide the long-term viscous behaviors. For all specimens the stretch power parameter is set to c_C = 0. The initial shear modulus of network (A) is decreased to capture the stabilized peak stress level from the prediction by the exponential fit, and the initial shear modulus of network (C) μ_C is decided by the peak stress decay from the first cycle to the stabilized level recorded in the experiments. The viscosity scaling constant Z_C is determined by fitting the peak stress decay rate obtained from simulation to the experimental data. The stress exponent parameter m_C is obtained such that the creep behavior can be best captured.