SUBJECT-SPECIFIC MODELS REVEAL THE EXISTANCE OF A RELATIONSHIP BETWEEN MORPHOLOGY OF THE ANKLE JOINT COMPLEX AND ITS PASSIVE MECHANICAL PROPERTIES

Abstract

The morphology of the bones, articular surfaces and ligaments and the passive mechanical characteristics of the ankle complex were reported to vary greatly among individuals. The goal of this study was to test the hypothesis that the variations observed in the passive mechanical properties of the healthy ankle complex are strongly influenced by morphological variations. To evaluate this hypothesis six numerical models of the ankle joint complex were developed from morphological data obtained from MRI of six cadaver lower limbs, and from average reported data on the mechanical properties of ligaments and articular cartilage. The passive mechanical behavior of each model, under a variety of loading conditions, was found to closely match the experimental data obtained from each corresponding specimen. Since all models used identical material properties and were subjected to identical loads and boundary conditions, it was concluded that the observed variations in passive mechanical characteristics were due to variations in morphology, thus confirming the hypothesis. In addition, the average and large variations in passive mechanical behavior observed between the models were similar to those observed experimentally between cadaver specimens. The results suggest that individualized subject-specific treatment procedures for ankle complex disorders are potentially superior to one-size-fits-all approach.

INTRODUCTION

The morphology of the bones, articulating surfaces and ligaments of the human ankle joint complex (AJC) was reported to be highly variable. For example, the anterior and medial articulating facets of the subtalar joint may be distinct or may blend into one surface (Barbaix et al., 2000; Bunning and Barnett, 1965; Gupta et al., 1977); the inclination and size of the sustentaculum tali vary from subject-to-subject (Sarrafian, 1983); ligaments, such as the calcaneofibular ligament, have variable insertion areas, and their orientation can range from vertical to posterior (Sarrafian, 1983). These morphological variations could be a main cause for the large variations observed in joint mechanics(Lundberg et al., 1989; Siegler et al., 1988b). They could influence the mechanical consequences of ligament injuries and may partially explain why some individuals are more predisposed to chronic ankle or subtalar instability than others (Barbaix et al., 2000). They may influence the outcome of surgeries such as joint fusion or joint replacement.

Despite the potential importance of this morphology-passive mechanics relationship, a review of the literature indicates that it has not been previously studied either experimentally or through numerical models. Models that incorporate subject-specific morphological data provide a convenient framework to explore this relationship since material properties, loading and boundary conditions can be kept identical between models thus isolating and identifying the contribution of morphology. Previous AJC models were unsuitable to study the morphology–passive mechanics relationship for a variety of reasons. Many did not include morphological data relying instead on simplified mechanical joint analogues such as one or two fixed revolute joints or four-bar linkages (Leardini et al., 1999; Scott and Winter, 1993). Other models, based on finite element techniques, incorporated morphology and tissue material properties (Bandak et al., 2001; Camacho et al., 2002; Cheung et al., 2005; Ledoux, 2000). However, these models were limited to loading conditions that produced small displacements (e.g., axial loading (Ledoux, 2000)), thus they only explored a small portion of the 3D envelope of motion of the AJC. Furthermore, these models were based on morphological data from a single subject, thus they were not used to explore effects of morphological variations.

The goal of the present work was to develop a 3D, image-based modeling framework and to use it to explore the existence of a relationship between morphological and passive mechanical variations of the AJC. The long-term goal, beyond this study, is to use this modeling framework to develop customized treatments of the AJC based on subject-specific morphology.

We present in this paper the development and evaluation of 6 models that were constructed using morphological data from 6 cadaveric specimens. The models were evaluated through a comparison of the passive mechanical behavior of each model with the experimental data from each corresponding specimen. This evaluation was used to address the hypothesis that the passive range of motion of the AJC is strongly influenced by morphological variations. In addition, the models were evaluated by comparing their average passive mechanical behavior with average experimental data obtained from an independent group of 15 cadaveric specimens. Passive mechanical behavior included range of motion, non-linear load-displacement characteristics and hysteresis during cyclic loading.

MATERIALS AND METHODS

Development of the Models

Structural Components

Six models of the AJC were developed from MRI data obtained with a 1.5 Tesla commercial GE Signa MRI scanner from six non-pathological un-embalmed cadaveric legs (average age 71.5 years, 2 males and 4 females). The scanning protocol consisted of a 3D Fast Gradient Echo pulse sequence with a TR/TE/flip angle of 11.5 ms/2.4 ms/60°, a 512 × 256 in-plane acquisition matrix, a 731.2 receiver bandwidth, and a 180mm × 180mm field of view. Sixty 2.1 mm-thick contiguous sagittal slices were collected to cover the foot from the medial to the lateral aspect. Consequently, the spatial resolution was 0.35mm × 0.7mm × 2.1mm. (Siegler et al., 2005).

3D renderings of the bones and identification of insertion sites of ligaments was achieved using an image processing software 3DVIEWNIX™ (Udupa et al., 1994). The 3D rendering process included operator-steered segmentation (Falcao et al., 1998) for identifying the boundaries of the bones followed by interpolation and filtering (Udupa et al., 1994) of the 2D binary bone images to obtain 3D surface models of the bones (Fig.1). These were imported into Geomagic Studio™ (Geomagic, Inc., Research Triangle Park, NC) where they were further smoothed, meshed (an average of 9825 ± 1475 surface triangles per bone), converted into stereolithographic format and imported into the dynamics software–ADAMS™ (Mechanical Dynamics, Inc., Ann Arbor, MI) (Fig. 2).

Fig. 1.

Comparison of bone surface renderings after image processing in 3DVIEWNIX (A) and after processed image was imported into ADAMS (B).

Fig. 2.

Medial view of all hindfoot models in the neutral position.

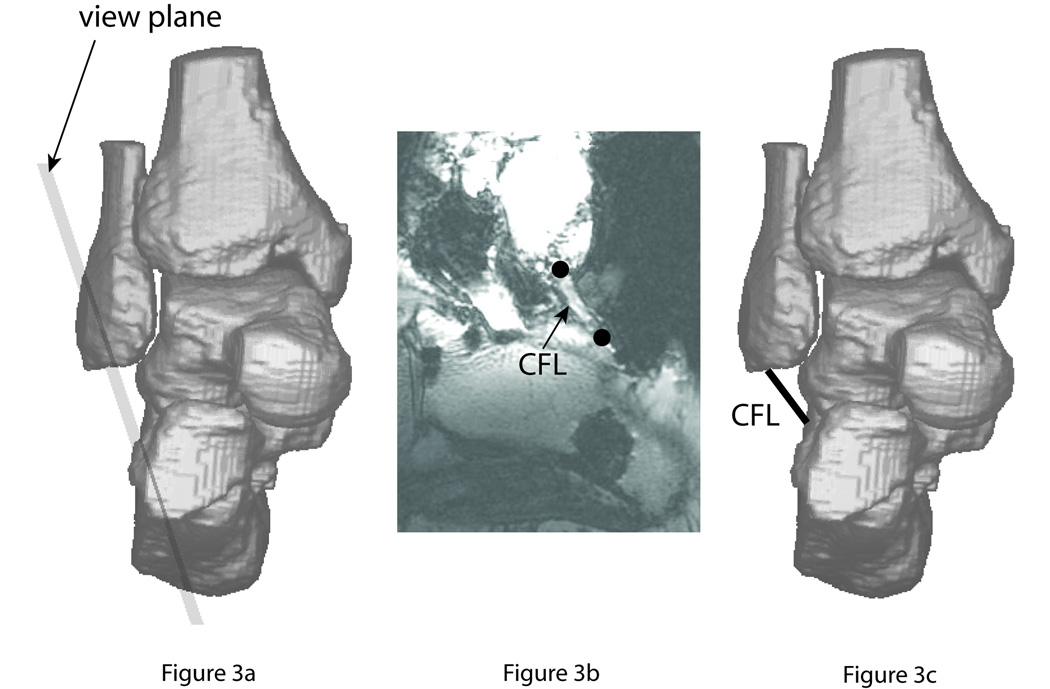
Identification of the insertions sites of ligaments was performed using a re-slicing algorithm (Fig. 3). The user moved a visible plane on the computer screen to an approximate orientation allowing visualization, after the new set of slices was created parallel to the chosen plane, of a selected ligament along its entire length (Fig. 3b). The user then marked the insertion sites of the ligament in the new slices, and the information was used to create a corresponding ligament element in the AJC model (Fig. 3c). A few trial-and-error cycles were typically required for the operator to successfully complete this process for each ligament. Collateral ligament diameter (Siegler et al., 1988a) (between 3.5 and 7.6 mm) was greater than the largest MRI voxels’ spatial dimension (2.1 mm), ensuring identification of these structures using the re-slicing algorithm.

Fig. 3.

Procedure for identifying the ligaments in the MRI.

Mechanical Components

The ligaments of the AJC were represented with single or multiple line elements depending on their geometries (Fig. 4). Cylindrical ligaments with relatively small diameter-to-length ratio such as the CFL (ratio = 1.3) (Siegler et al., 1988a) were represented by a single element. Ligaments with relatively large diameter-to-length ratio, such as the ITCL (ratio = 45.2) (Siegler et al., 1988a) were represented by multiple elements. This multi-element representation enabled the simulation of recruitment of different ligament fibers under different loading conditions.

Fig. 4.

3D rendering in ADAMS showing the representation of the ligaments used in the model. The lateral collateral group consisting of three ligaments: the anterior talofibular ligament – ATFL, the calcaneofibular ligament – CFL, and the posterior talofibular ligament – PTFL (2 elements). The medial collateral group consisting of three ligaments: the anterior tibio-talar ligament – ATTL, the tibio-calcaneal ligament – TCL (2 elements), and the deep posterior tibio-talar ligament – PTTL (4 elements). The subtalar group consists of two ligaments: the cervical ligament – CL (4 elements), and the interosseos ligament – ITCL (10 elements).

The material properties of each ligament element were described using a tension-only, non-linear load (T)–strain (ε) relationship (Eq. 1).

$$T\left(\epsilon \right)=A\left(e^{B\epsilon }-1\right)+c_1\mathit{\epsilon ̇}$$ Equation 1

The constants, A and B, were fit (in the least square error sense) to experimental data reported in the literature (Funk et al., 2000). The damping coefficient was selected as c₁ = 1 N*s/mm, based on experimental stress relaxation data reported for the hindfoot ligaments (Funk et al., 2000). Initial ligament lengths were taken as the distance between insertions sites in the neutral position.

The mechanical properties of the subtalar ligaments are unknown. Therefore, they were assigned the same material properties as the PTTL since they have similar gross morphological appearance (Sarrafian, 1983) and similar cross-sectional areas (Siegler et al., 1988a).

Contact at the joints including location, penetration depth and penetration velocity was detected using the Robust and Accurate Polygon Interference Detection (RAPID) search algorithm (Gottschalk et al., 1996). RAPID, which was part of the ADAMS software. The force developed between contacting articular surfaces was defined as a non-linear function of penetration depth, x, and penetration velocity, ẋ.

$$\mathit{\text{Force}}={\mathit{\text{kx}}}^e+c_2\mathit{ẋ}$$ Equation 2

The penetration depth was scaled by a stiffness constant k, based on the compressive modulus of cartilage at the distal tibia and talar dome. (E=0.374 MPa) (Treppo et al., 2000). The modulus term was scaled by the cartilage thickness which was assumed uniform throughout each joint (Al-Ali et al., 2002) (ankle joint = 0.8 mm, subtalar joint = 0.73 mm, talo-fibular joint = 0.8 mm) and the average area of the triangular elements comprising the bone surfaces (1 mm²). The penetration depth, x, was also scaled by an exponent e, which modeled the nonlinear compressive properties of cartilage (Park et al., 2004). This term was assigned a value of 9 to ensure that penetration would not exceed cartilage thickness at each articulation. The damping coefficient’s value was chosen as c₂=2 Nmm/sec to match previously reported data (Izambert et al., 2003). The articular surfaces were assumed to be frictionless (Eberhardt et al., 1991; McCutchen, 1962).

The mass, location of the center of mass, principle mass moments of inertia and directions of the principle axes of the bones were calculated automatically using the ADAMS software. The calculations were based on the average densities of cortical and cancellous bone(Mow and Hayes, 1991), assumed equal distribution of the material throughout each bone geometry, and on the points comprising the surface of each bone geometry. It was estimated that because of the relatively slow movements involved in the simulations, the effect of inaccuracies in bone mass distribution on the resulting passive mechanics were negligible.

The equations of motion governing model behavior were generated and solved using ADAMS. The simulation process required setting up run time, solver parameters (GSTIFF integrator (Gear, 1971), integrator error 0.01, a maximum integrator step size 0.001 seconds, initial simulation step size of 0.0001 seconds), and initial, boundary and loading conditions. These conditions were set to correspond to the experimental conditions used to evaluate model behavior.

Evaluation of the Models

Evaluation of the models was based on a specimen-by-specimen comparison (n=6) to test the main hypothesis, and a group mean comparison (n=15) to evaluate average model behavior. This second group excluded the 6 specimens used to create the models.

For the specimen-by-specimen comparison, the experiments consisted of loading the AJC in anterior drawer and in inversion simulating clinical tests for evaluating integrity of the ATFL and CFL(Johannsen, 1978). Each specimen was positioned in neutral in an MR compatible loading device (Siegler et al., 2005) with the tibia and fibula fixed and the calcaneus constrained to move only in the direction of the applied loads and scanned. Next, an anterior drawer force, increasing from zero to 150N was slowly applied, the device was locked in the maximally loaded position, and the loaded specimen was rescanned. The procedure was repeated for inversion with a maximum moment of 3.4 Nm.

The rotations and translations of the calcaneus from neutral to each maximally loaded configuration were computed from the MRI data (Siegler et al., 2005). We used the principal axis coordinate system of the calcaneus expressed relative to the tibia in the neutral and loaded configurations to calculate the rotation about the screw axis (Kinzel et al., 1972; Udupa et al., 1998). To compute translations at the ankle joint complex, we calculated the relative translation of the origin of the calcaneus with respect to the origin of the fixed tibia. We then expressed the components of this translation in the coordinate system of the tibia. We used the component of translation projected onto the anterior-posterior oriented axis of the tibia as our measure for anterior drawer.

Root Mean Square (RMS) error of the differences between model and experimental results for all six data sets was computed. In addition, a one way repeated measures analysis of variance (ANOVA) with a Tukey post-hoc test (P < .05) was used to determine the presence of significant differences between model predictions and the experimental data. The standard deviation was used to estimate the level of variability across experimental data and across model predictions.

The rotational passive displacement-load properties in all 3 anatomical planes (plantarflexion/dorsiflexion, inversion/eversion and internal/external rotation) were used for model evaluation based on comparison of group means. These properties were obtained using an experimental set-up (Chen et al., 1988; Siegler et al., 1988b) that allowed the application of pure moments to the calcaneus. These loads were slowly cycled between 0 and ±8 Nm. The tibia and fibula were fixed and the motion of the unconstrained talus and calcaneus were recorded via a 3D sonic digitizer (Chen et al., 1988; Siegler et al., 1988b). We calculated all primary and coupled rotations from the kinematic data using the Grood and Suntay parameters as applied to the ankle joint, subtalar joint and AJC as described in our previous work(Siegler et al., 1988b; Siegler et al., 2005).

Model evaluation was based on comparison of the rotations produced at maximal loads at the ankle joint, the subtalar joint, and the AJC in the direction of the applied load (primary ROM) and in directions other than that of the applied load (coupled ROM). Qualitative assessment of the ability of the model to capture the viscoelastic and non-linear behavior of the AJC was observed from the cyclic displacement-load characteristics.

A one factor ANOVA with a Tukey post-hoc test (P < .05) was used to determine whether there were significant differences between the model predictions and the experimental data for all the primary ROM parameters at the AJC, ankle joint and subtalar joint, and coupled ROM parameters at the AJC.

RESULTS

The one-to-one comparison of the ROM of the models with their corresponding physical experiment in inversion yielded an RMS error of 1.8° (Table 1). There was no significant difference between model prediction and experimental data (P=0.964). The ROM of the AJC varied across experiments (min = 6.4°, max = 23.9°,) and across models (min = 7.7°, max = 23.2°). Standard deviations were 5.9° for the model and 6.7° for the experiments.

Table 1.

One-to-one comparison of each of the six model predictions and the corresponding experimentally measured ROM of the ankle joint complex in inversion and anterior drawer.

	AJC
	Inversion [Deg]		Anterior Drawer [mm]
Specimen	Model	Experiment	Model	Experiment
1	13.4	11.8	6.2	6.6
2	12.8	13.9	4.5	5.7
3	15.0	11.3	8.4	4.8
4	23.2	23.9	10.3	6.5
5	22.0	21.8	8.7	10.1
6	7.7	6.4	7.1	3.3
AVE	15.7	14.9	7.5	6.2
STDV	5.9	6.7	2.0	2.3

In anterior drawer, the one-to-one comparison of the ROM of the models with their corresponding physical experiment yielded an RMS error of 2.8mm. There were no significant differences between model prediction and experimental data (P=0.864). The ROM of the AJC varied across experiments (min = 3.3mm, max = 10.1mm), and across models (min = 4.5mm, max = 10.3mm). Standard deviations were 2.0 mm for the model and 2.3 mm for the experiments.

The comparison of the average model predictions with the independent average experimental data revealed no significant differences for primary ROM at the AJC in all directions except for dorsiflexion, where model prediction was significantly higher (P=0.032) than the experimental average (Table 2).

Table 2.

Model and experimental results of the averages and standard deviations of the motion patterns of the ankle joint complex - primary ROM (in bold) and coupled ROM.

			Rotation at the AJC in degrees
			Plantarflexion		Dorsiflexion		Inversion		Eversion		Internal Rot		External Rot
			Model	Exp	Model	Exp	Model	Exp	Model	Exp	Model	Exp	Model	Exp
	Plantarflexion	AVG	39.6	40.9			9.0			0.4	0.4	2.4
		STDV	11.7	4.3			9.5			4.7	7.6	3.5
	Dorsiflexion	AVG			35.3	24.7	0.4			0.5		0.4	0.6
		STDV			7.0	3.2	4.6			5.0		5.8	9.6
	Inversion	AVG	26.0	22.4			16.1	16.3			11.0	21.9
		STDV	6.3	9.1			8.5	3.9			12.5	8.7
	Eversion	AVG		11.8	17.1				13.2	15.9			0.0	11.0
		STDV		10.3	13.1				5.8	4.4			7.0	6.9
	Internal Rot	AVG	8.1	14.4			5.6	5.9			26.6	29.8
		STDV	9.7	6.9			5.1	2.8			11.7	7.6
	External Rot	AVG		9.8	17.3				8.4	6.3			15.0	22.0
		STDV		9.4	8.0				6.6	2.7			5.6	6.0

Significant differences between average model predictions and average experimental data for primary ROM at the ankle joint were observed only in dorsiflexion (P=0.022) and in internal rotation (P=0.039) (Table 3). At the subtalar joint, there were no statistically significant differences in primary ROM between average model predictions and average experimental data.

Table 3.

Model and experimental results of the averages and standard deviations of the primary ROM of the ankle and subtalar joints corresponding to the primary ROM of the ankle joint complex.

		AJC		AJ		STJ
		Model	Experiment	Model	Experiment	Model	Experiment
Plantarflexion [Deg]	AVG	39.6	40.9	26.9	32.7	10.6	9.0
	STDV	11.7	4.3	7.9	3.8	7.1	4.1
Dorsiflexion [Deg]	AVG	35.3	24.7	27.4	19.7	6.5	5.4
	STDV	7.0	3.2	4.2	4.0	4.9	3.2
Inversion [Deg]	AVG	16.1	16.3	4.8	4.6	12.8	15.0
	STDV	8.5	3.9	5.9	4.9	7.9	5.7
Eversion [Deg]	AVG	13.2	15.9	4.7	6.3	9.8	8.5
	STDV	5.8	4.4	1.8	4.4	5.1	3.4
Internal Rot [Deg]	AVG	26.6	29.8	7.0	14.3	20.7	15.6
	STDV	11.7	7.6	4.7	3.7	12.4	6.6
External Rot [Deg]	AVG	15.0	22.0	5.1	12.2	10.5	10.2
	STDV	5.6	6.0	4.6	3.7	7.1	5.4

Both models and experimental average data showed negligible coupling (less than 2.4°) associated with dorsiflexion and plantarflexion with an exception of an average of 9 ± 9.5° of inversion coupled with plantarflexion exhibited by the models (Table 2). Both models and experiments showed plantarflexion and internal rotation coupled with inversion with no significant differences between model predictions and experimental data. The experimental data showed, on average, plantarflexion and external rotation coupled with eversion. In contrast, the models predicted only dorsiflexion coupled with eversion (P<0.001). Both the models and the experiments showed plantarflexion and inversion coupled with internal rotation and eversion coupled with external rotation.

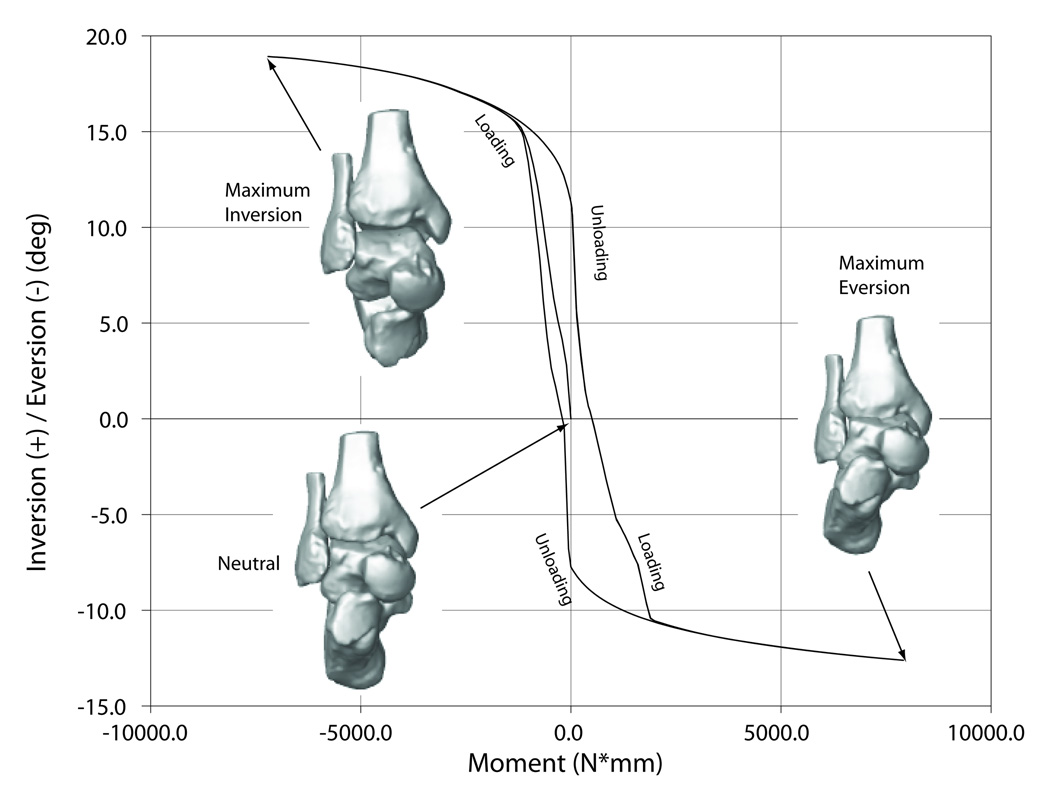
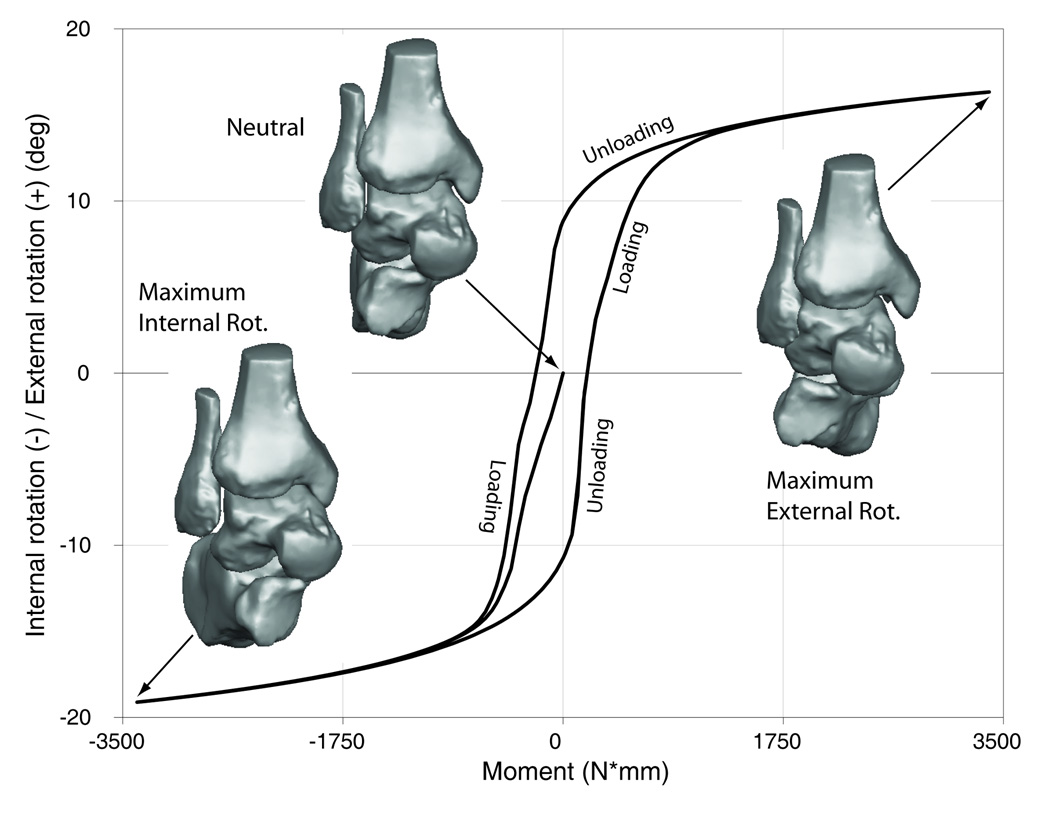
Similar to the average experimental data, all six models exhibited non-linear displacement-load behavior, which manifested as high initial flexibility around neutral that decreased towards the extremes of the range of motion, and viscoelastic behavior, which manifested as hysteresis (Fig. 5).

Fig. 5.

Displacement-load characteristics of the ankle complex in the different loading directions.

5a - anterior drawer.

5b – dorsiflexion/plantarflexion.

5c – inversion/eversion.

5d – internal rotation/external rotation.

DISCUSSION AND CONCLUSIONS

We have described the development and evaluation of models of the AJC using subject-specific morphological data from multiple specimens. Model evaluation was based both on comparing model behavior to experimental data on a specimen-by-specimen basis and on the basis of population average.

The passive mechanical behavior of each of the six models was found to closely match the experimental data obtained from each of the six corresponding specimens. Since all models used identical material properties and were subjected to identical loads and boundary conditions, it was concluded that the observed variations in passive mechanical characteristics were due to variations in morphology, thus confirming the hypothesis. For example, the pronounced differences in morphology of the sustentaculum tali of specimen 6 (larger, more conforming, and spanning a large portion of the medial border of the subtalar joint) compared to those of the other five specimens (Fig. 2) likely correspond to the large difference in ROM in inversion of specimen 6 (2 to 3 times smaller) compared to the others. This specific observation supports the claim (Barbaix et al., 2000; Wagner et al., 1992) that variations in the geometry of the sustentaculum tali across a population are related to variations in the stability of the subtalar joint and may explain the predisposition of some individuals to develop subtalar instability.

Given the strong dependency of passive joint mechanics on joint morphology, certain surgeries (e.g., ankle or sublalar joint fusion, joint replacement or ligament reconstruction) may produce different results in different individuals. For example, patients with morphological features that cause a less constrained subtalar joint may be able to tolerate an ankle joint fusion better than those with a more constrained joint due to the ability of their subtalar joint to compensate for the lost ankle motion. Thus, individualized clinical treatment of hindfoot disorders may be superior to a generic, one-size-fits-all approach.

Average model predictions of ROM were found to be in close agreement with values reported previously (20° –50° plantarflexion; 13° – 33° dorsiflexion; 15° – 20° inversion; 10° – 17° eversion; and 24° external rotation) (Allinger and Engsberg, 1993; Cass et al., 1984; Kjaersgaard-Andersen et al., 1991). In addition, the large variations of primary and coupled ROM observed between the models were similar to those observed experimentally between cadaveric specimens and were similar to those reported by others in the past (Hintermann et al., 1994; Kjaersgaard-Andersen et al., 1991; Lundberg et al., 1989; Siegler et al., 1988b; Siegler et al., 2005). The models also captured the experimentally well known non-linear mechanical behavior of human joints (Kjaersgaard-Andersen et al., 1991; Siegler et al., 1996; Tohyama et al., 1995) including hysteresis during loading-unloading cycles.

The disagreements between model predictions and experimental data may be due to lack of information on the material properties of the subtalar ligaments, and exclusion of pretension in the representation of the ligaments. However, as such data become available, they can be easily incorporated in the models. Sensitivity analyses could be used in the future to identify the impact of these unknown parameters on model predictions.

In conclusion, morphological subject-specific models of the AJC are necessary to correctly predict individual hindfoot passive mechanical behavior. Such models could be used as subject-specific surgical planning and optimization tools for surgeries such as ankle or subtalar arthrodesis. For example, surgical parameters such as orientation and amount of bone resected in joint fusions could be optimized for each individual patient based on prescribed criteria such as minimization of ligament loads, or achievement of a desired ROM. They can also be used to identify morphological features that place certain individuals at increased risk for pathological conditions such as chronic ankle or subtalar joint instability.