Compound Poisson Approximation of the Number of Occurrences of a Position Frequency Matrix (PFM) on Both Strands

Abstract

Transcription factors play a key role in gene regulation by interacting with specific binding sites or motifs. Therefore, enrichment of binding motifs is important for genome annotation and efficient computation of the statistical significance, the p-value, of the enrichment of motifs is crucial. We propose an efficient approximation to compute the significance. Due to the incorporation of both strands of the DNA molecules and explicit modeling of dependencies between overlapping hits, we achieve accurate results for any DNA motif based on its Position Frequency Matrix (PFM) representation. The accuracy of the p-value approximation is shown by comparison with the simulated count distribution. Furthermore, we compare the approach with a binomial approximation, (compound) Poisson approximation, and a normal approximation. In general, our approach outperforms these approximations or is equally good but significantly faster. An implementation of our approach is available at http://mosta.molgen.mpg.de.

1. Introduction

Transcription factors (TFs) play a key role in gene regulation by binding to genomic sequences (Alberts et al., 2002). Binding sites of TFs are often represented as position frequency matrices (PFMs) introduced by Stormo et al. (1982). Genome annotation and the understanding of genetic regulatory networks require the assessment of the statistical significance of TF binding site occurrences. Reliable results for the significance are given by p-values derived from the count statistic (Denise et al., 2001).

Exact calculation of the count distribution can be done by generating functions (Gentleman and Mullin, 1989; Hertzberg et al., 2005; Kleffe and Langbecker, 1990; Régnier, 2001) or other methods (Beckstette et al., 2006; Bejerano et al., 2004; Staden, 1989; Zhang et al., 2007). Unfortunately, the calculation of exact p-values is NP-hard (Zhang et al., 2007). Hence, many efforts are concerned with the asymptotic word count distribution using normal approximations (Brendel et al., 1986; Leung et al., 1996; Waterman, 2000; Prum et al., 1995), (compound) Poisson approximations (Chryssaphinou and Papastavridis, 1988; Godbole, 1991; Schbath, 1995; Robin, 2002; Roquain and Schbath, 2007), and large deviation results (Denise et al., 2001; Reinert et al., 2000). Both the exact and the asymptotic approaches require the enumeration of all compatible words which are words encoded in the PFM yielding a hit on the sequence. The number of compatible words grows exponentially with the length of the PFM. Thus, calculation is inefficient for long PFMs.

In this article, we propose an approximation based on the compound Poisson distribution for the number of occurrences of a PFM without enumerating all compatible words. Furthermore, we incorporate both strands of the DNA molecules, which is important for palindromic PFMs. We explicitly consider dependencies of overlapping hits. The approach outperforms existing approximations (Schbath, 1995; Waterman, 2000; Roquain and Schbath, 2007). In contrast to the most recent exact calculation (Zhang et al., 2007), its complexity neither depends on the number of compatible words nor on the sequence length.

The next section introduces the statistical framework (Rahmann et al., 2003) and develops the approximation for the count statistic. Since we explicitly model the self-overlap of the PFM that results in dependencies, we can calculate two characteristic values for the self-overlap and the palindromicity of a PFM. Finally, the simulation for the comparison of the approaches is described, as well as the competing approaches (Schbath, 1995; Waterman, 2000; Roquain and Schbath, 2007). The Results section contains the comparison of the approaches. A discussion and an outlook are given in the final section.

2. Methods

Our statistic for the number of binding sites uses the probability of a detected binding site, as well, as the self-overlap of the PFM. For example, a PFM with the consensus “CTAACT” has a higher probability to find two hits overlapping in two positions than to find two independent hits. Counting the number of binding sites while taking care of the self-overlap has already been discussed for a single word (Guibas and Odlyzko, 1981; Robin and Schbath, 2001) and a small set of given words (Reinert et al., 2000). We give two reasons for avoiding the Chen-Stein approach proposed by Reinert et al. (2000) and Roquain and Schbath (2007): First of all, the enumeration of all compatible words encoded in the PFM is computationally demanding and only possible for small PFMs. Second, the incorporation of the complementary strand can lead to two hits at one position. In terms of word counting, this means that the words in the set of compatible words are not necessarily different contradicting one important assumption for the (compound) Poisson approximation. Therefore, we use the discrete nature of the PFM score to compute the probabilities of overlapping hits (Pape et al., 2006). Based on these probabilities, we use a generalization of the Poisson distribution to model overlaps. We couple a probability vector for the number of hits with a Poisson distribution. This is a so called stopped-sum distribution (Johnson et al., 1995) or compound Poisson distribution. This distribution is widely used for word count statistics.

2.1. The PFM framework

Each PFM represents a binding site. It contains specific probabilities for each nucleotide at every position. We assume that the binding sites of each TF are described by only one PFM. An extension to more than one PFM is not trivial but, in general, possible. The position specific scoring matrix (PSSM) Ψ_{κ, σ} is chosen to be the log-likelihood ratios of the nucleotide distribution of the PFM and the background probabilities π_σ for every position κ and for nucleotides σ ∈ Σ. We denote the length of the PSSM by ℓ. The background model is an i.i.d. model only defined by the GC content. Since we require the distribution of hits on both strands to be equal, we need this restriction. We call this a symmetric i.i.d. background model which can also be justified by Chargaff's second law. Furthermore, in contrast to coding sequence, there is no motivation to handle both strands in the upstream region differently.

Using the PSSM, we can assign a score to every position of the potential binding site depending on the observed nucleotide. Sliding a window of length ℓ over the sequence σ₀ … σ_n and summing up the scores in each window, yields a score S_j for every position j of the sequence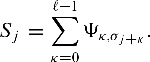

From now on, we consider the letters σ_j of the sequence as random variables. Thus, S_js are random variables, too.

Considering the complementary strand requires additional notation: In general, we use the same variables with a prime for this purpose. We call the strand of the corresponding gene the 5′-3′ strand. Correspondingly, the complementary strand is called the 3′-5′ strand. In contrast to the 5′-3′ strand, we assign a hit to the position at the complementary strand where the actual hit ends (Fig. 1). This means, that refers to the score of the nucleotides 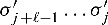where 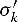denotes the complementary letter of σ_k.

FIG. 1.

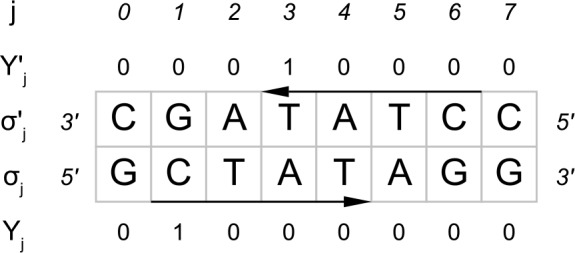
The figure clarifies notation: The lower 5′-3′ strand is the leading strand. Given a motif CTAT, there are two overlapping occurrences on the shown sequence region. 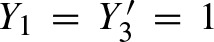indicate a hit starting at position 1 on the leading strand and another hit ending at position 3 on the complementary strand. This definition of Y_j and 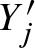simplifies notation.

We call a position a hit if the corresponding window yields a score s higher than a certain threshold t . Denoting a hit at position j by the indicator random variable Y_j = 1, we obtain the definition: Y_j : = 1[S_j ≥ t]. Similarily, a detected binding site on the complementary strand at position j is denoted by 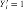(Fig. 1).

2.2. Statistics for binding site detection

The threshold t controls the probabilities α and β given by 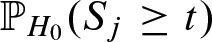and 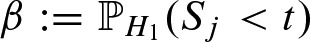where H₀ is the null model corresponding to a random sequence and H₁ the model for the binding site. Using the convolution of the position-specific score distributions according to the background model (Rahmann, 2003), we can compute the threshold t depending on the choice of α. The parameter α has to be very small as the expected number of false positives on a sequence of length n is 2n · α for both strands. To control the power of the PFM to seperate compatible from non-compatible words, we set the threshold as described by Pape et al. (2006). There, the threshold is set such that α and β are balanced on a reasonable level. In general, the count statistic is robust against the actual threshold as long as neither all positions are hits nor none because α is incorporated into its computation.

2.3. Count statistic

After this review of the detection of binding sites, we move on to the statistics of the number of detected binding sites. As previously mentioned, the probability of detecting a binding site by chance in a symmetric i.i.d. sequence model is α. Hence, the indicator random variables Y_j and 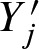have a Bernoulli distribution with 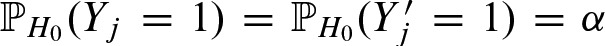and 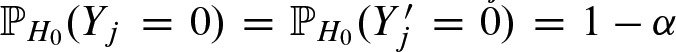. Let X denote the number of binding sites in a region of length n of a sequence:

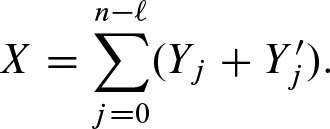
In fact, Y_j and 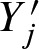are defined on an infinite sequence but in practice we are concerned with finite sequences. Hence, the dependencies of Y_j and 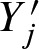are different at the beginning and the end of the sequence. These boundary effects are negligibly small under the rare hit assumption (Barbour et al., 1992). The rare hit assumption holds because we set α and the threshold t such that only a very small fraction of all possible words have a score greater than or equal to the threshold.

Now, we can compute the enrichment of binding sites on a sequence using the probability 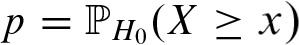as p-value where x is the observed number of binding sites. Although we know the probability of Y_j and we assume the symmetric i.i.d. sequence model, calculation of p is not straightforward due to dependencies between Y_js and 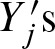. The dependencies are caused by self-overlap of the PFM and by incorporation of the complementary strand both leading to overlapping binding sites.

2.4. Computing probabilities of clumps

Dealing with overlapping hits requires a refined vocabulary: A hit and its overlapping hits together can be defined as a clump. The size of the clump corresponds to the number of contained overlapping hits. Also a single hit without any overlaps is called a clump of size 1. Thus, a clump is a left- and right-maximal set of overlapping hits on both strands.

Now, we incorporate the notion of clumps into our definitions. We assume that the number of clumps N is distributed as a Poisson random variable 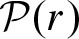with unknown rate parameter r. The size Z_i of the clumps are assumed to be identically and independently distributed by an unknown probability vector 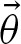. (Fig. 2). Both assumptions can be justified by the fact that they hold for word counting (Robin, 2002). The number of counts per sequence is given by 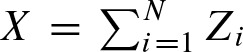. X follows a compound Poisson distribution .

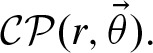FIG. 2.

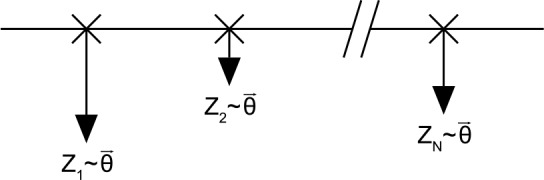
The horizontal line symbolizes the sequence. At certain position (marked by a cross), a clump occurs. The size of each clump is modeled by an i.i.d. probability vector. The number of clumps N is distributed as a Poisson random variable .

In the remaining part of this section, we show how to compute approximations of the unknown parameters of rate r and the probability vector 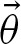. First of all, we reduce the computation of r to the computation of 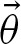. Then, we start with the probability θ₁ of having exactly one hit. Based on θ₁, we recursively compute the remaining parameters. Furthermore, the analysis of the resulting formulation discovers two characteristic values describing the self-overlap of the PFM.

2.4.1. Computing the rate r

The parameter r is the rate of clump occurrences. We cannot use the probability α of a false positive directly to compute it because α is the probability for hits including overlapping hits. In contrast, we need the rate for non-overlapping hits which is equal to the rate of clumps. Using the law of total probability, we obtain

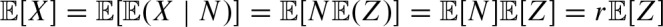
Thus, we can express r in terms of 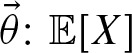is the expected number of hits. The probability of a hit by chance is α as we defined the threshold in this way. Hence, the expected number of hits is given by the fact that a hit can occur at each sequence position on each strand, thus

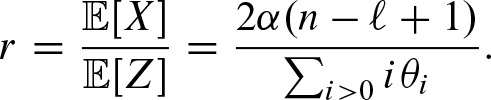
2.4.2. Parameters for the probability vector

The probability vector 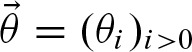contains probabilities for the different sizes of clumps i > 0. Here, we show how to compute approximations 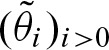of these probabilities. At first, we focus on one strand of the sequence only. Subsequently, we extend the approach to deal with the complementary strand as well.

θ₁ corresponds to the event that there is exactly one hit at a certain position j while no overlapping hits occur given the hit at position j. Using the fact that an overlapping hit is a hit within the range of the length ℓ of the PFM, we obtain

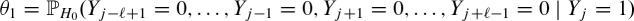
The conditional probability on the right hand side of Equation (2) is hard to compute because the events in the collection ({Y_{j + k} = 0})_{− ℓ + 1≤k ≤ ℓ−1, k≠0} are not independent, given {Y_j = 1}. However, in a first order approximation we pretend that conditional independence holds and compute

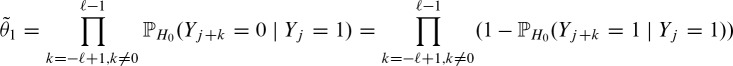
Due to the symmetric i.i.d. random sequence, we can prove the symmetry 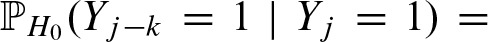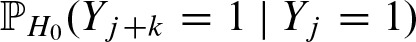by applying the law of conditional probabilities and substituting j = j′ + k:

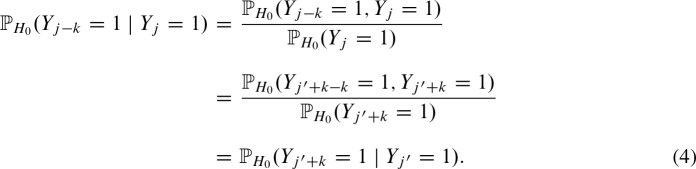
Symmetry follows due to the symmetric i.i.d. background model. Thus, we obtain for Equation (3)

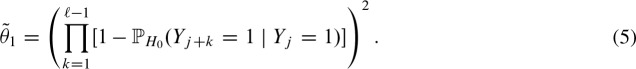
Next, we extend the approach to both strands by continuing to assume conditional independence for all hits (Pape et al., 2006) and simplify notation by

where Y′ refers to the hit random variable on the other strand. Hence, Equation (5) becomes

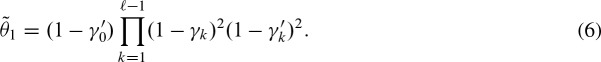
This term contains the probability of two overlapping hits 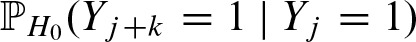for k as given above in γ_k, and correspondingly in 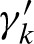for the reverse strand. Thus, we need to compute the probability of the score at position j + k exceeding the threshold given there is a hit at position j: 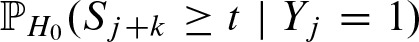. In previous work (Pape et al., 2006), we used the nucleotide distribution given by the PFM for the overlapping part. Unfortunately, the performance of the approximation varies signficiantly between different PFMs. Therefore, we model the dependencies explicitly.

2.4.3. Probability of two overlapping hits

Here, we compute the exact value for 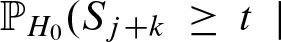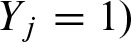. The event {Y_j = 1} is equal to the event {S_j ≥ t) due to the definition of the indicator random variable Y_j. We define the set of scores which are assumed to be integers by

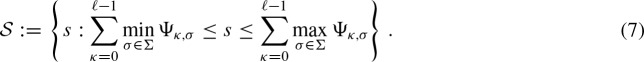
Then, the scores greater than or equal to the threshold can be defined by 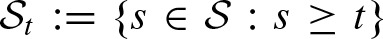. Using these definitions, we can express 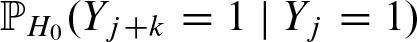in terms of a two-dimensional score distribution

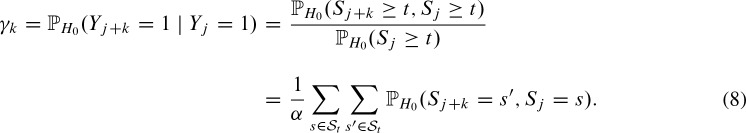
The overlapping probabilities 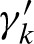can be computed correspondingly.

Considering the scores as state space, the S_js become a first-order Markov chain (Fu and Koutras, 1994) because the score only depends on the score of the previous position. Hence, Equation (8) can also be written in terms of its transition matrix to the kth power. For the sake of simplicity, we focus on the two-dimensional score distribution for each k. This distribution can be computed by the two-dimensional convolution of the position specific score distributions. An efficient dynamic programming algorithm is presented in Section 2.5.

2.4.4. Probability of an i-clump with i > 1

We recursively compute the probability 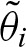to have a clump with exactly i hits for i > 1. Without loss of generality, we assume that we count hits starting with 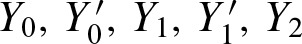, and so on. Considering a clump of size two, the first overlapping hit at a clump position j can either occur in the interval k ∈ [j + 1, j +ℓ − 1] on the same strand or in the interval k ∈ [j, j +ℓ − 1] on the opposite strand. The idea is to cancel the probability in Equation (6) for each position k and to replace it with the probability of a hit at this position. We denote these extension factors ξk for a hit on the 5′-3′ strand and 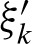for a hit on the 3′-5′ strand. We obtain for a pair of hits for 0 < k < ℓ

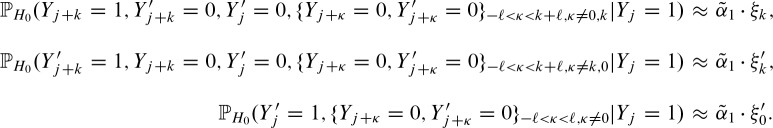
For the definitions of ξ_k, 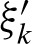, and 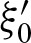, it is important to note that one also has to replace the probability at the other strand at position k with the probability 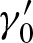for an exact palindromic hit at position k of the old hit except the new hit is on the 3′-5′ strand. In this case 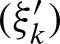, an exact palindromic hit is not possible (because we would have counted the hit before). We also replace the probabilities for hits at the subsequent positions given the hit at position j with the probabilities of a hit given the hit at j + k. Lastly, one has to extend the positions without a hit to the positions covered by the new hit but not by the former hit. Thus, we obtain the definitions for 0 < k < ℓ

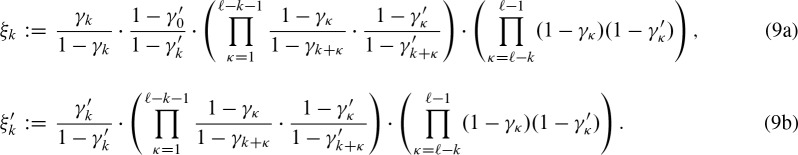
For the other strand, we must not replace the exact palindromic hit because the hit is already on that strand. We have an overlapping hit if any of these encoded events occur. Thus, we can sum up the terms (Fig. 3)

FIG. 3.

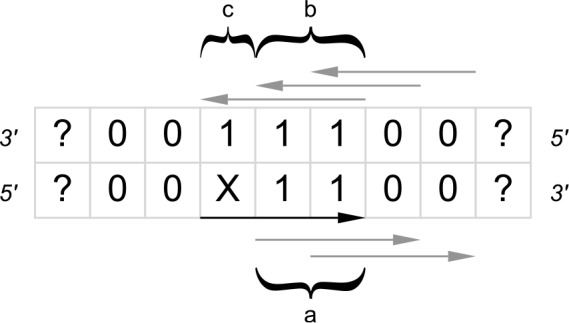
X and the black arrow indicate the given hit, while 0s indicate where no hit is allowed, 1 denotes the possibility of an overlapping hit (marked by grey arrows), and ? is a hit or no hit. The letters a, b, and c label the three different type of hits: type (a) is a hit on the same strand, type (b) hits on the complementary strand but not palindromic, and type (c) is the palindromic hit.

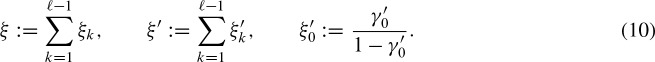
We split up the different types of hits into a, b, and c because they differ with respect to which hit can follow (see Fig. 4). Type (a) encodes a hit on the 5′-3′ strand. The hit can be followed by a hit on the same strand (a), a hit on the complementary strand (b), or an exact palindromic hit (c). Type (b) is a hit on the 3′-5′ strand excluding an exact palindromic hit. After it, types (a) and (b) can follow. An exact palindromic hit is not possible as the hit itself is on the 3′-5′ strand. Type (c) stands for the exact palindromic hit. Everything but another exact palindromic hit can follow.

FIG. 4.

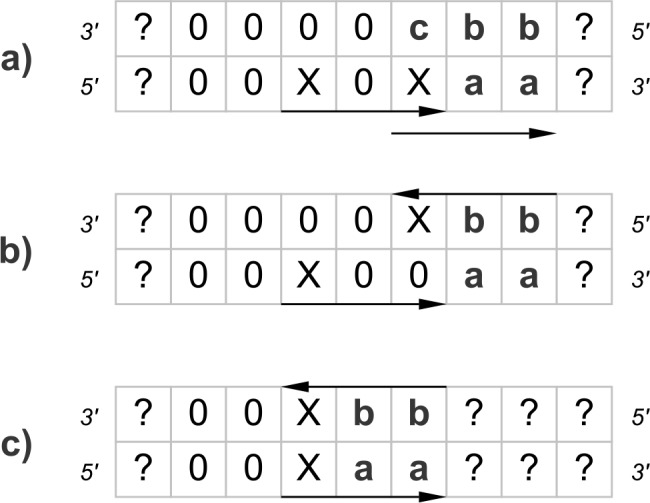
The figure shows the three different types of hits (a), (b), and (c) in a situation of two previous hits. Furthermore, for each type of hit, the possible subsequent type of hit is indicated by the corresponding identifier (a, b, or c). While (a) and (b) can occur after each type of hit, (c) can only occur after type (a).

Thus, an additional hit of type (a) can be preceded by a hit of type (a), (b), or (c). For (b) the same logic applies. In contrast, a palindromic hit (c) can only occur after a hit of type (a). Without these considerations, we would allow more than two hits at the same position. This gives us a linear system of recurrences to compute an approximation of 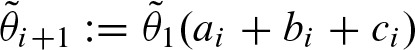. Again, assuming that conditional independence holds, we have 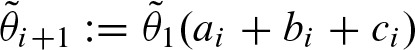, where

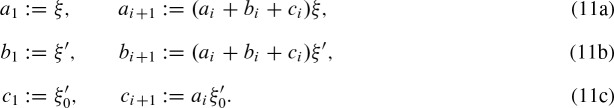
2.4.5. Closed formula

Although the above formulas suffice to compute an approximation for 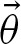, the reformulation as a closed formula and its further analysis reveals interesting insights. At the end, we obtain two characteristic values which describe the self-overlap of the PFM.

We can write the recursive formulas (11a) to (11c) by matrix notation for i > 0

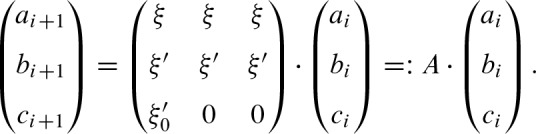
Thus, we get the closed formula for i ≥ 0 with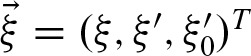

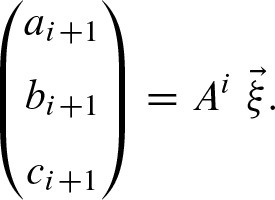
Furthermore, we obtain 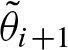using the recurrence formula for i > 0

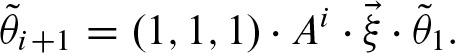
We decompose A = B⁻¹ Λ B where B contains the eigenvectors of A and the diagonal matrix Λ the corresponding eigenvalues λ₁, λ₂, λ₃ given by

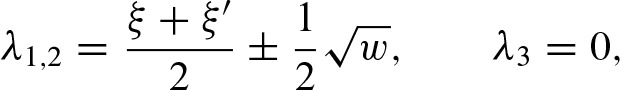
with 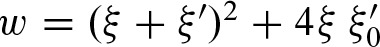. Hence, we can denote 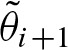in terms of the eigenvalues

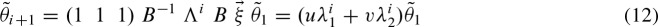
where u and υ are computed by solving the linear system

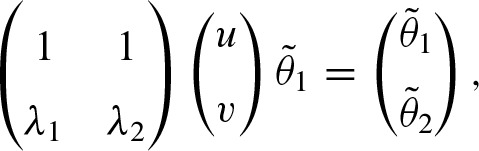
whereby 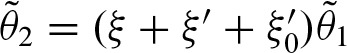using the recursive formula. Finally, we obtain the solution

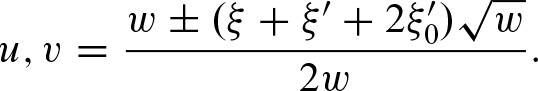
In addition to the benefits of a closed formula, the expression in Equation (12) shows that the asymptotics of the clump size only depend on the first two eigenvalues λ₁, λ₂. Obviously, the following inequalities hold: λ₂ ≤ 0 and λ₁ > −λ₂. Hence, the series 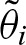converges to zero, 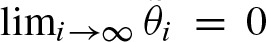, if λ₁ < 1. This condition holds if most of the words of length ℓ do not exceed the threshold which is in practice always true. In most cases, we can also assume λ₁ < 1 since for λ₁ > 1 we can transform the PSSM and the threshold to its complement which yields λ₁ < 1 and correspondingly use the complementary statistics.

2.4.6. Two characteristic values for PFMs

The eigenvalues can be used as descriptive values for the PFM: We call a PFM a palindrome if it allows two hits at the same position on both strands. Considering a PFM which is not a palindrome, we have 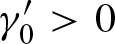, thus, 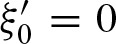. Hence, matrix A has only rank 1 and we only obtain one non-zero eigenvalue λ₁ and u = 1. Therefore, 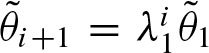decreases exponentially. Higher values of λ₁ decelerate convergence. Since 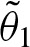is the probability of a clump of size one, which means that no overlap occurs, and λ₁ corresponds to the probability of an overlap, obviously 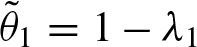holds. Hence, the clump size has a shifted geometric distribution. This case is similar to the compound Poisson model for one word considering only one strand described by Robin (2002). Discarding the complementary strand always leads to λ₂ = 0 and then both models are equivalent.

A palindromic PFM has λ₂ < 0 since 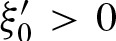. If 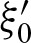dominates the eigenvalues we obtain λ₂ ≈ −λ₁. In addition, it follows that v ≈ −u. Thus, 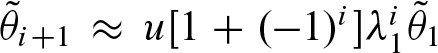. This leads to 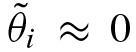for odd i. It indicates that the probability of an odd clump size is approximately equal to zero. As we assumed a palindromic PFM with a very high probability of a palindromic hit, one almost always detects a hit on both or neither strands. In summary, λ₁ describes the speed of convergence of 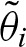to zero and −λ₂ correlates with the tendency of palindromic hits.

2.4.7. The p-value for number of hits

Now, we can compute the approximations of the probability vector 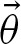and the rate parameter r using Equation (1). Using the approximations for the parameters, we can compute the distribution for the number of hits x ≥ 0. Since the number of hits X is distributed as 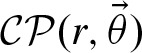we can apply formulas for the compound Poisson distribution (Kemp, 1967):

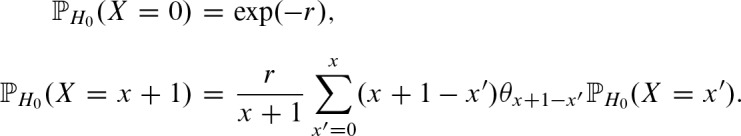
The p-value for the occurrence of x ≥ 0 hits is computed by:

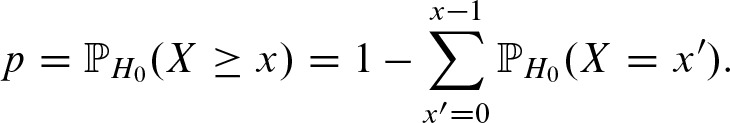
2.4.8. The p-value for number of clumps

The underlying Poisson process for the count statistic is given by 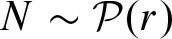. Since N is the number of clumps, one can use 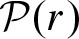to compute p-values p′ for clumps as the count entity. In this case, we only need to compute the rate r. Equation (1) can be approximated by

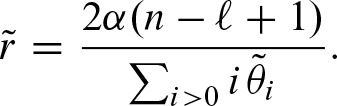
Next, we show how to compute 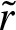efficiently by substituting the sum under the assumption −1 < λ₂ ≤ 0≤ λ₁ < 1. Using the expression in Equation (12), we obtain

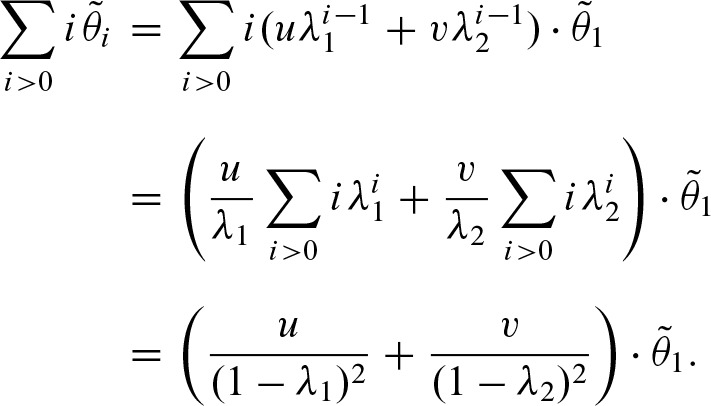
Again, this equation has an interpretation in terms of the self-overlap of the PFM. In case of a non-palindromic PFM, the second term is equal to zero since λ₂ = 0 and, therefore, υ = 0. From λ₂ = 0, it also follows that w = (ξ + ξ′)², hence, u = 1. Since a non self-overlapping PFM has λ₁ near to zero, the above equation is equal to 1. Thus, the expected value of the clump size is equal to 1 and the rate for clumps is 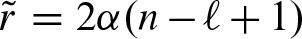. Furthermore, 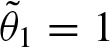contains all the weights of the probability vector. Then, . Hence, applying the derived statistic to a non self-overlapping PFM leads to a Poisson process with rate .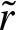

2.5. An efficient algorithm for computing overlap probabilities

In Equation (8), we have to compute the joint event of two scores greater than or equal to the threshold. Given a position j and a shift k, the two scores induce a two dimensional distribution. The first component is the score s of the PSSM starting at position j. The second component is the score s′ of the PSSM beginning at position j + k. As an example, consider a PSSM which only accepts ‘CC’. In the case of a shift k = 1, the score s′ can only exceed the threshold if s is above the threshold. Thus, both scores are not independent for 0 ≤ k < ℓ. Since scores are the sum of the position specific scores Ψ_i, we can decompose the score into each pair of positions j + i and j + i + k which point to the same sequence position, and, thus, to the same nucleotide. Then, pairs of scores are independent. Hence, we can use a dynamic programming algorithm.

The dynamic programming approach is often used for the computation of the one dimensional score distribution (Staden, 1989; Claverie and Audic, 1996; Wu et al., 2000; Rahmann, 2003; Rahmann et al., 2003; Beckstette et al., 2006). We extend this approach to two dimensions. Let 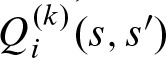denote the probability for a score s at the first i + 1 positions of the PSSM and a score s′ at the first i + 1 − k positions of the PSSM shifted by k positions. We compute this value by summing over the probabilities of the last step i − 1 which yield a score s and s′ after observing any nucleotide with its respective score at step i . With Ψ_κ,. : = 0 for κ < 0 or κ ≥ ℓ, we obtain for 0 ≤ k < ℓ and 0 ≤ i < ℓ + k

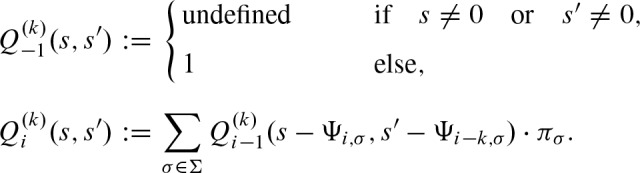
After the last step, 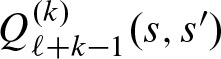contains the probability to observe score s starting at position j and score s′ starting at position j + k. Therefore, 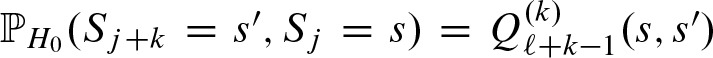and, hence, we can solve Equation (8).

2.5.1. Speed improvement

The practical running time of the algorithm can be improved significantly by some modifications. The last k steps do not modifiy the scores starting at position j since Ψ_κ,. = 0 for κ ≥ ℓ. Hence, instead of the k two-dimensional convolutions, we can obtain 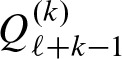in one step by using the one dimensional convolution of the last k positions (Fig. 5). Since Equation (8) sums over all scores s starting at position j, we can do the summation before adding the remaining scores:

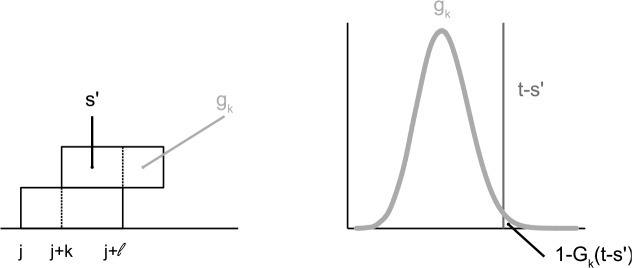
FIG. 5.

The left part of the figure shows the sequence with two overlapping hits at position j and j + k. The score of the overlapping part of the second hit is given by s′. The score of the non-overlapping part is a random variable whose distribution is the convolution of the position-specific scores of the remaining positions of the PFM g_k. The right part of the figure visualizes this distribution and the probability of the second hit 1 − G_k(t − s′).

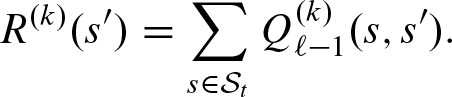
Let f_κ denote the position specific score distribution at position κ of the PSSM and g_κ denotes the score distribution for the non-overlapping part for a shift k:

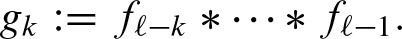
Using the recursion g_{k + 1} = g_k * f_{ℓ − k−1}, we can use a dynamic programming approach for computing the convolution. Denoting the cumulative distribution for g_k with G_k, we can rewrite Equation (8) by:

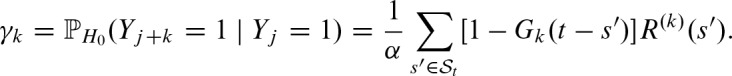
We can further improve the speed by removing scores in each step of the calculation of Q which are too small to reach the threshold (see Beckstette et al. [2006] for the one-dimensional case). Hence, we define intermediate thresholds t_i by

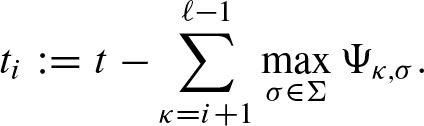
In each step i, we can remove scores s < t_i and s′ < t_{i − k}. In addition, one can merge scores which will exceed the threshold t for sure. The corresponding intermediate thresholds 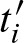are defined analogously to Equation (13) by substituting min with max. Then, in each step i, scores 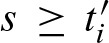and 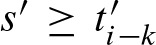can be merged.

We can further speed up the algorithm by enhancing the effect of these improvements (see Beckstette et al. [2006] for a similar idea). Processing positions of the PFM with high information content first, discards many scores which can't exceed the threshold at all in the first steps. In addition, indefinite positions (processed at the end) often do not change the score significantly such that either the score has already been discarded or the score surely exceeds the threshold. This reduces the size of Q significantly.

In summary, the algorithm takes advantage from both a high and a low threshold t: On the one hand, the higher the threshold, the more scores can be removed in the beginning steps because scores will not be able to exceed the threshold at all. On the other hand, a low threshold yields many scores which surely exceed the threshold. As those scores can be merged, the number of different scores (size of Q) stays low.

2.5.2. Time complexity

The complexity of the algorithm for the computation of Q depends on the length of the PFM ℓ, the size of the set 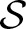of all scores, and the alphabet size 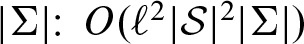. The length of the PFM ℓ and the alphabet size |Σ| are primitives and, therefore, cannot be reduced any further. In contrast, 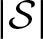is a constructed set, hence, we have to analyze its complexity. It is important to note that the size of 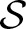is independent of the threshold and, therefore, of the number of compatible words. Furthermore, 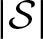does not grow exponentially with increasing length of the PFM because the scores of a new column are only added to the overall scores. This only increases the size of 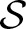linearly with increasing PFM length.

3. Computational Results

3.1. Data

3.1.1. Sequences

To compare the new statistic with previous approaches, we use a simulation study. We simulate 100,000 sequences of length 10,000 with an arbitrarily selected GC content of 40% using an i.i.d. model. These sequences are annotated by binding sites of artificially constructed and real PFMs (see next paragraph). Counting the number of hits/clumps per sequence and computing the frequency for each count, one retrieves a simulated count distribution for each PFM. Comparing the simulated count distribution with the theoretically approximated distributions, we can easily assess the accuracy of the approximations, as well, as comparing the approximations between themselves.

3.1.2. PFMs

We artificially construct four PFMs, each of them carrying a certain characteristic regarding self-overlap (Crooks et al., 2004) (Fig. 6):

FIG. 6.

Sequence Logos from left to right and top to bottom: “nothing,” “palindrome,” “repeat,” “repeatpalindrome,” and “M00950.”

• Nothing: a PFM without any self-overlaps

• Palindrome: a PFM with a likely hit on the complementary strand

• Repeat: a PFM where the suffix matches the prefix such that one expects overlapping hits in a chain

• Repeatpalindrome: a combination of the palindrome and the repeat.

Furthermore, we arbitrarily pick one real PFM from TransFac (Matys et al., 2003) with a self-overlapping structure to show that the gain in accuracy is relevant in practice. We select the palindromic PFM M00950 corresponding to the binding site of the MADS domain protein AGAMOUS-like 15 (AGL15) (Tang and Perry, 2003).

In a pre-processing step, we regularize the PFMs to ensure strictly positive frequencies. Thus, we add pseudocounts to the position specific distributions according to the information content of the position (Rahmann, 2003). In fact, positions with low information content are shifted towards the background distribution. For positions with high information content, the difference to the background distributions is enforced. Then, we compute PSSMs from the regularized PFMs by taking the log-likelihood ratio of the nucleotide frequencies of the binding site and the background model.

We set the threshold for each PFM according to Pape et al. (2006) ensuring that the probability α₅₀₀ for at least one false positive in a sequence of length 500 for any higher threshold is 10% at maximum. Thus, in the case that one cannot balance α₅₀₀ and β, we obtain α₅₀₀ ≈ 0.1. Furthermore, in case of a balanced threshold, α₅₀₀ and β will not be exactly equal due to the discrete nature of the score and, thus, of α₅₀₀ and β. Applying this procedure, the number of compatible words for PFM “nothing” using a threshold t = 136 with α₅₀₀ = 0.013 and β = 0.01 is 1,142 only containing unique words. PFM “palindrome” (t = 99, α₅₀₀ = 0.129 and β = 0.325) encodes 48 words based on 24 unique words while PFM “repeat” (t = 128, α₅₀₀ = 0.118 and β = 0.553) has 702 words without any non-unique words and, finally, “repeatpalindrome” (t = 125, α₅₀₀ = 0.157 and β = 0.649) yields 50 words from which 25 are unique. Thus, the compatible set of both PFMs with a palindromic structure contain each word twice (for each strand once). The Transfac PFM ‘M00950’ (t = 118, α₅₀₀ = 0.0785 and β = 0.0747) has 846,976 words with 429,812 unique words.

3.2. Standard count statistics

In this section, we present the previous count statistics that we compare our approach with. They are applied on the set of compatible words after removing redundant words such that the assumptions are met.

3.2.1. Binomial and Poisson approximation

A simple approach to compute the p-value for the number of hits is the assumption of independence between hits. Then, the number of hits have a binomial distribution. We obtain the p-value p_B = 1 − B(x; 2n, α) where B(·) is the cumulative binomial distribution with parameters x for the number of successes, 2n the number of trials and α the probability of success. The number of successes corresponds to the number of detected hits. As we consider hits on both strands and assume independence, the number of trials is twice the length of the sequence.

A statistic for the number of clumps can also be derived. A clump is defined such that it does not overlap with a previous clump. Hence, the probability α′ of a clump can be calcuated by

α′ = 2(1 − α)^{2ℓ − 1}α + (1 − α)^{2ℓ − 2} · α².

The term (1 − α)^{2ℓ − 1} is the probability of no hit on the ℓ − 1 positions before the hit on both strands plus no hit on the complementary strand at the current position. As a hit can occur on both strands, we multiply by the factor 2. The last term corresponds to a clump starting with a palindrome. The p-value is computed by .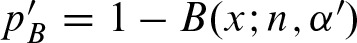

Both binomial distributions can also be approximated by a Poisson distribution with parameter r_P ≈ 2(n − ℓ + 1)α for hits and 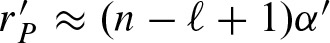for clumps.

3.2.2. Chen-Stein Poisson approximation

Reinert and Schbath (1999) present a Chen-Stein Poisson approximation for the occurrences of multiple words. We can transform the PFM hit statistic to a word counting problem using the set of compatible words . Then, we can use the Chen-Stein approach to compute the Poisson approximation. There are several problems using this approach: First, enumeration of all words in is not possible for longer PFMs. Second, the number of words in might be fairly high which leads to large bounds on the total variation distance. Third, incorporation of the complementary strand can only be achieved by extending by all reverse complementary words. This almost always breaks the necessary assumption for the approximation that no word is a substring of any overlap of any two other words. Therefore, we only use the approximation for the clump statistics because there only the weaker assumption that no word is a substring of any other word has to be fulfilled. This is indeed the case except for a palindrome.

In Roquain and Schbath (2007), an improved compound Poisson approximation is proposed. Since this approach only requires that no word is a substring of any other word for both the clump and the hit distribution, we also include this approach in the comparison. Still, the main drawback to enumerate all the compatible words remains. Furthermore, the approach involves multiple matrix multiplications where the two dimensions of the matrices are equal to the number of compatible words. This leads to numerical instabilities for large sets of compatible words.

3.2.3. Normal approximation

We can use another multiple word occurrence approach for the number of hits. Waterman (2000) shows how to compute the limiting covariance matrix as well as the limiting mean value. These values can be used as parameters for a normal distribution. Again, we need the set of all compatible words for the computation.

3.3. Comparison of the different approaches using simulated data

We compare the approaches based on the p-values since the statistic will mainly be used to retrieve p-values for observed number of hits/clumps. We present them after taking the logarithm to base ten. Therefore, the p-p plots show log-p-values. The x-axis always refers to the simulated distribution while the y-axis corresponds to the approximated distribution. The more points are located on the diagonal, the better the approximation. Furthermore, points below the diagonal correspond to underestimation of the p-values while points above the diagonal are conservative approximations.

3.3.1. Artificial PFMs

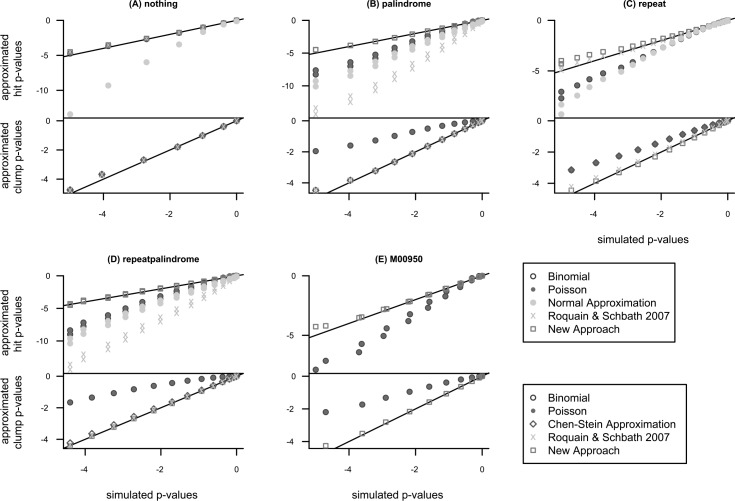
Figure 7A shows the p-p plots of the “nothing” PFM. Most of the points lie on the diagonal. Furthermore, there is no big difference between the binomial and Poisson approximations, as well, as the the approach from Roquain and Schbath (2007) and the new approach. Only for very small p-values, there is a subtle difference between the approximations: The binomial and Poisson approaches seem to slightly outperform the others. However, the very small p-values are based on very few sequences because such high numbers of hits/clumps do not occur very often. Therefore, we ignore these points for interpretation. Only the normal approximation underestimates the p-values systematically. As the Poisson approximation works better, obviously, the rare word assumption is fullfilled instead of the normal approximation assuming often-occurring words. The results for clumps do not differ. As there are no overlaps, both the hit and the clump statistics are similar. Obviously, the new approach captures this non-self-overlap

FIG. 7.

Comparison of the simulated p-values (x-axis) with the approximated p-values (y-axis) in a log-scale p-p plot.

Figure 7B contains the results for the PFM “palindrome.” The single distribution lying on the diagonal corresponds to our new approach. The binomial, Poisson, the normal and the Roquain and Schbath (2007) approach substantially underestimate the p-values. For the binomial and Poisson approximation, this is due to the fact that the number of hits is higher since the PFM tends to hit on both strands the same time. Furthermore, there are always pairs of points very close to each other. This is due to the hit on the complementary sequence which always occurs with a hit on the 5′-3′ strand: Having one hit on one strand implies a second hit on the other strand. Obviously, only the new approach can deal with this. In contrast, the Roquain and Schbath (2007) approach does not lead to a reasonable approximation. Since the set of compatible words contains each word twice but the approach can only deal with a set of unique words, the weak approximation is not surprising. For statistics of clumps, the Roquain and Schbath (2007) and the new approach lie fairly on the diagonal, as well, as the Chen-Stein approximation. Here, the approximations for the Roquain and Schbath (2007) and the Chen-Stein approach work because for clumps redundant words in the set of compatible words have no influence.

Figure 7C compares the approximations for the “repeat” PFM. Binomial, Poisson, and normal approximations look very similar. Neither these nor the other two approaches lie on the diagonal, although the Roquain and Schbath and the new approach are more similar to the diagonal. In general, the Roquain and Schbath estimates are lower than the ones from the new approach and fit better to the diagonal. In addition, both approaches are conservative in contrast to the others which significantly underestimate the p-values. The approximations for the clump statistic are similar except that the new approach slightly underestimates the p-values for small number of clumps and overestimates them for higher number of clumps. In general, while the Roquain and Schbath approach obtains higher estimates leading to a more accurate approximation for small number of clumps but a slightly weaker approximation for higher number of clumps. The other approaches overestimate the p-values significantly. Here, the Chen-Stein approximation performs as bad as the binomial/Poisson approximation since the assumption that no word is a substring of the concatenation of any other two words is extensively violated.

In Figure 7D, the comparisons for the “repeatpalindrome” PFM is shown. In general, the approximations are similar to the ones of the “palindrome” PFM with some influence of the “repeat” PFM. This shows that the new approach can deal with both types of similarity at the same time in contrast to all other approaches. Only the new approach leads to a reasonable approximation of p-values for the number of hits.

3.3.2. PFM M00950

The results for the Transfac PFM M00950 are shown in Figure 7E. Using the balanced threshold to obtain a probability of a false positive in a region of 500 bp equal to 7.6%, the number of unique compatible words is equal to 429,812. Therefore, comparison with the Chen-Stein approximation, the normal approximation, and the Roquain and Schbath approach is not possible because these statistics could not be computed in a feasible amount of time. The comparison with the simulated p-values shows that the new approach fits very well. In contrast, the binomial/Poisson approximations show the typical significant deviation we have already seen for the artificial PFMs. Hence, in such a realistic framework, the new approach is the only possiblity to compute the count statistic without simulations.

3.4. Characteristic values

Table 1 shows the characteristic values for each PFM. The “nothing” PFM has a low first eigenvalue while the second eigenvalue is equal to zero. Since the PFM has no self-overlap, these two characteristic values confirm the analysis given in the method section. For the “palindrome” PFM the equation λ₁ ≈ −λ₂ holds because the only self-overlap is given by the the palindromic property of the PFM. The “repeat” PFM has a much higher first eigenvalue than the “nothing” PFM since it has a strong repeat-structure. Since there is no palindromic feature within the PFM, we obtain λ₂ = 0. In constrast, the “repeatpalindrome” PFM contains both self-overlaps, thus, λ₂ < 0 but λ₁ ≠ −λ₂. Finally, the PFM “M00950” has also a clear palindromic self-overlap. All these observations are confirmed by the sequence logos (Fig. 6) and the resulting count statistics (Fig. 7). Thus, the characteristic values describe the self-overlapping features well. In the given cases, the self-overlap is clear for illustration purposes but in more difficult cases they shed light on the self-overlapping structure.

Table 1.

The Two Characteristic Values Given by the Eigenvalues of Matrix A for Each pfm

	λ1	λ2	Comment
Nothing	0.0123	0.0000	λ1 small, λ2 = 0
Palindrome	0.0016	−0.0016	λ1 small, λ2 = −λ1
Repeat	0.2599	0.0000	λ1 large, λ2 = 0
Repeatpalindrome	0.1792	−0.1526	λ1 large, λ2 ≈ −λ1
M00950	0.0455	−0.0435	λ2 ≈ −λ1

4. Discussion

We have proposed a new approximation for the count statistic of PFMs. In contrast to most previous works, we incorporate the complementary strand, which introduces further dependencies of overlapping hits. Due to explicit modeling of these dependencies, as well as dependencies between overlapping hits on the same strand, we are able to compute precise p-values for any PFM. Furthermore, we have shown how to compute two characteristic values describing the tendency of overlaps and palindromic hits of a given PFM with the same algorithm. The time complexity neither depends on the sequence length nor on the number of compatible words. Therefore, the algorithm is very efficient. It might be further improved using the Fourier transform with the convolution theorem (Press et al., 1992; Keich, 2005).

Comparison with other approaches shows that our approach has highest accuracy. Furthermore, most of the competing approaches enumerate all compatible words . Since grows exponentially with the length of the PFM the overall-running time is exponential. Hence, the normal approximation (Waterman, 2000), the Chen-Stein approach (Reinert and Schbath, 1999), as well as the Roquain and Schbath (2007) approach, and the exact approach (Zhang et al., 2007) cannot generally be applied in practice (see Supplementary Material for a comparison of the running time at http://mosta.molgen.mpg.de).

A major drawback of the new approach is the restricted background model. So far, we only use a symmetric i.i.d. model defined by the GC content. Therefore, the statistics are symmetric between both strands. Further studies will show whether more complicated background models which conserve the symmetry can be used as well.

The count statistic can be used for the upstream annotation of genes as well as mapping of PFMs to certain genome regions. An extension of the approach to two or more PFMs yield many more applications like p-values for co-occurrences and similarity between PFMs (Pape et al., 2008).

Disclosure Statement

No competing financial interests exist.