Systematic construction and prediction of the arrangement of the strands of sandwich proteins

Abstract

The problem of predicting the three-dimensional structure of a protein starting from its amino acid sequence is regarded as one of the most important open problems in biology. Here, we solve aspects of this problem for the so-called sandwich proteins that constitute a large class of proteins consisting of only β-strands arranged in two sheets. A breakthrough for this class of proteins was announced in Kister et al. (Kister et al. 2002 Proc. Natl Acad. Sci. USA 99, 14 137–14 141), in which it was shown that sandwich proteins contain a certain invariant substructure called interlock. It was later noted that approximately 90% of the observed sandwich proteins are canonical, namely they are generated by certain geometrical structures. Here, employing a topological investigation, we prove that interlocks and geometrical structures are the direct consequence of certain biologically motivated fundamental principles. Furthermore, we construct all possible canonical motifs involving 6–10 strands. This construction limits dramatically the number of possible motifs. For example, for sandwich proteins with nine strands, the a priori number of possible canonical motifs exceeds 360 000, whereas our construction yields only 49 geometrical structures and 625 canonical motifs.

1. Introduction

It is well known that the three-dimensional structure of a protein is completely determined from the sequence of its amino acids. However, the problem of predicting the three-dimensional structure (often called tertiary structure) of a protein starting from a given amino acid sequence remains open.

Proteins appear in the form of certain topological structures called folds. It has been suggested that the limited number of folds is perhaps due to the existence of rules that dictate the folding of a polypeptide chain. Furthermore, it has been suggested that such rules can be divided into two types: rules that predict the so-called secondary elements of the protein, namely the β-strands and the α-helices, and rules that give the arrangement of strands and helices into a tertiary structure. Although, the question of the complete description of the first type of rules remains open, the prediction of the strands and the helices starting from a given amino acid sequence has now become a routine procedure of approximately 80% accuracy (Rost 2001). However, even for proteins that consist of only β-strands (and no α-helices) such as the so-called sandwich proteins, the problem of predicting the arrangement of the strands in the space remains open. In this direction, structural biologists have used the occurrence of the so-called Greek key introduced by Richardson (Chirgadze 1987) as well as several different algorithms based on neural networks and Markov models (Chothia & Finkelstein 1990; Yue & Dill 2000).

The β-strands of sandwich proteins are arranged in two planes. Regarding the structure of sandwich proteins, a breakthrough was announced in Kister et al. (2002), in which it was shown that sandwich proteins contain a certain supersecondary substructure called interlock. Following this discovery, it was noted in Fokas et al. (2004) that approximately 90% of the observed secondary structures of sandwich proteins are canonical, i.e. they satisfy certain structural rules (see rules I–III of Fokas et al. (2004)). Furthermore, it was shown in Fokas et al. (2005) and Kister et al. (2006) that these rules are automatically satisfied provided that the canonical structure is generated from a certain geometrical structure.

In this paper, (i) we show that the existence of geometrical structures is a consequence of certain simple biologically motivated principles, (ii) we identify all possible geometrical structures, and (iii) we construct all possible canonical strand arrangements of sandwich proteins consisting of 6–10 strands.

2. Definitions and schematics

We first review some definitions of Fokas et al. (2005) and Kister et al. (2006). We then introduce the notion of a path that is important for the subsequent analysis. Finally, we present several schematics for the secondary structure of a given sandwich protein, which is referred to as a motif.

2.1 Cyclic numbering

Throughout this work, n denotes the number of strands of a sandwich protein. Although our analysis is valid for any positive integer n, we concentrate on 6≤n≤10 since this is the range of the strands of most observed sandwich proteins. We assign the numbers 1, 2, …, n to the n strands. Two consecutive strands i and i+1 are connected with a loop directed from i to i+1 and denoted as i→i+1. We use cyclic numbering (‘addition modulus n’), e.g. if i=n the next strand i+1=n+1 is strand 1. Furthermore, the strand n is connected with the strand 1 by the fictitious loop n→1.

We recall some definitions of Fokas et al. (2005) and Kister et al. (2006): sheets are the two planes in which the strands of a sandwich protein are arranged. Neighbouring strands (NSs) are two strands in the same sheet with no other strand between them. A jumping pair (JP) is a pair (i, i+1) of two consecutive strands that belong to different sheets. If both strands of a JP lie at the same end (left or right) of the two sheets, then the JP will be an edge JP (EJP). Otherwise, it is an internal JP (IJP). An interlock consists of two IJPs, (i, i+1) and (j, j+1), such that i and j are NSs, i+1 and j+1 are also NSs and if i is to the left (right) of j then i+1 is to the right (left) of j+1. We also define as a ‘jumping loop’ and as an ‘edge jumping loop’ the loop i→i+1, where (i, i+1) is an IJP and an EJP, respectively.

2.2 Paths

For any two strands i and j, a path from i to j, denoted by i↦j, is the sequence of all consecutive strands and loops, in increasing order, beginning with i and ending at j.

Examples: the path i↦i+1 includes the loop i→i+1 and the two strands i and i+1; 3↦7 is the path 3→4→5→6→7; for n=9, 8↦2 is the path 8→9→1→2. By the ‘trivial path i↦i’, we define only the strand i, whereas by the ‘complete circular path i↦i’, we define the path i→i+1→⋯→n→1⋯→i, which contains all strands and loops. For any two strands i, j, i≠j, the two paths i↦j and j↦i, put together in this order, form the complete circular path i↦i.

2.3 Schematic representations

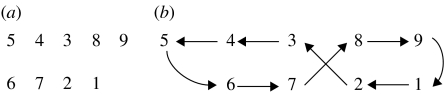
A typical representation of a motif is given by the example of figure 1a; the upper and lower sheets contain the strands 5, 4, 3, 8, 9 and 6, 7, 2, 1, respectively. Figure 1b provides an alternative schematic of the same motif, which also contains the connecting loops and the fictitious loop 9→1. In figure 1b, one can easily identify any path i↦j, such as the path 8↦2 mentioned earlier.

Figure 1.

(a,b) Two schematics of a motif consisting of n=9 strands.

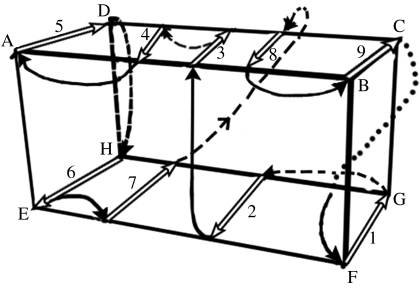
For our analysis, we will need more details about the orientation and the location of strands and loops, as shown in the more informative schematic of figure 2: the upper and lower sheets are located on the upper and lower planes ABCD and EFGH, respectively. The planes ABFE and DCGH will be referred to as the front and back planes, respectively. The planes ADHE and BCGF will be referred to as the left and right edges, respectively. Strands in each sheet are directed either from the front to the back planes or from the back to the front planes. Two strands with the same direction are called parallel, while two strands of opposite direction (i.e. one from the back to the front plane and the other from the front to the back plane) are called antiparallel. Loops connecting consecutive strands that are both either in the front or in the back planes are denoted by continuous and broken lines, respectively. For example, the loops 2→3 and 6→7 lie in the front plane, while 7→8 and 5→6 lie in the back plane. Note that 9→1 starts in the back plane and ends at the front one, i.e. it crosses from one plane to the other. It is clear that there exist a priori several choices for possible loop and strand orientations. One of these choices for the motif of figure 1a is shown in figure 2, where strands 3 and 4 are antiparallel, while strands 9 and 1 are parallel.

Figure 2.

Detailed schematic of an SP motif with n=9 strands.

2.4 Relative position of strands

Let k and m be two different strands and suppose that they do not form an EJP. Then the schematic specifies unambiguously whether k is to the left or to the right of m. Indeed, there exist the following possibilities for k and m: (i) they are in the same sheet, (ii) they are in different sheets and lie on opposite sides of an IJP, (iii) one of them is part of a JP and the other lies to the left or to the right of this JP, and (iv) they form a JP. For cases (i)–(iii), it is clear whether k is to the left or to the right of m. Regarding (iv), let us take, without loss of generality, m=k+1. If k−1 and m+1 lie on different sides of this JP, then the relative position of k, m is also well defined: if k−1 is on the left (right) and m+1 is on the right (left) of the JP (k, m=k+1), then k is also on the left (right) of m.

2.5 Path directions

We say that a path i↦j has right (left) direction or, equivalently, that it is a rightward (leftward) path, if for all consecutive pairs k, k+1 in this path, k is to the left (right) of k+1. Furthermore, if the path i−1↦i+1 has a right or left direction, then we also adopt this as the direction of the trivial path i↦i. For example, in figure 1b, the path 2↦5 and the trivial path 3↦3 are both leftward.

2.6 Direction change

If (k,  k+1) is a JP and both k−1 and k+2 are to the left (right) of this JP, then we say that this JP causes a direction change, namely the direction changes from rightward (leftward) to leftward (rightward).

3. Fundamental principles

We introduce three fundamental principles. These can be considered as the fundamental axioms, from which observed motifs can be constructed. These fundamental principles are consistent with the following basic biological requirement.

Folding takes place using only necessary and uncomplicated moves. Unnecessary jumps or moves that create complicated structures are avoided.

For the generation of a motif, it is necessary that there exists a change of direction. According to the definitions of §2, this can occur only at a JP. However, if this JP is not an EJP, it is easy to see that this direction change leads to more direction changes and more JPs. Based on the above, we postulate the following.

3.1 Fundamental principle 1

A direction change occurs only at an EJP.

Consider two JPs (i, i+1) and (j−1, j) contained in a rightward (leftward) path i↦j with no other JPs between them. This path leaves one sheet at strand i using the JP (i, i+1) and returns to the same sheet at strand j, using the JP (j−1, j). If i and j are NSs, we consider these two JPs as either unnecessary or fictitious because the above path could continue in its rightward or leftward direction from i to j without the need to change sheets, i.e. without these two JPs. Alternatively, the path can be viewed as lying entirely in the sheet of i and j, i.e. this sheet is schematically deformed so that the two JPs are fictitious.

3.2 Fundamental principle 2

There do not exist paths i↦j, which leave a sheet at the strand i using the JP (i, i+1), do not change direction and return to the same sheet at the strand j, using a second JP (j−1, j), where i and j are NS.

3.3 Fundamental principle 3

Loops do not overlap or cross each other. Furthermore, loops do not cross from the front (back) to the back (front) planes, with the possible exception of loops associated with EJPs.

This principle implies that the cases shown in figure 3a–e are not allowed. Similarly, the cases obtained from these figures when the left–right sides and/or the front–back planes are interchanged are also prohibited. It should be noted that, if the two consecutive strands involved in these examples are the strands (n, 1), then the loop n→1 is fictitious and in this case the violations do not take place.

Figure 3.

(a–g) Examples of unacceptable cases and (h) the EJP acceptable case. (a,b) Loops cross each other, (c–e) loops overlap and (f–h) loops cross from the front to the back plane.

We emphasize that several of the above cases have been discussed by other authors. In particular, the non-occurrence of crossing loops and of topological knots has been explicitly stated in Richardson (1977) and Lim et al. (1978). Furthermore, the prohibition of the cases figure 3c,d follows from the results of Efimov (1982, 1995), which state that the superhelices formed by three consecutive β-strands in a sandwich protein must be right-handed. Also, the prohibition of cases figure 3f,g follows from the fact that the dehydration of the NH and CO groups of a polypeptide chain is energetically expensive (e.g. Lim et al. 1978).

4. Geometric properties of motifs

In this section, we show that the fundamental properties postulated in §3 imply that motifs possess certain basic properties. It will be shown in §5 that these properties can be used for the systematic construction and the prediction of all such motifs.

If a motif of a sandwich protein satisfies the three fundamental principles postulated in §3, then: (i) Two consecutive strands lying in the same sheet are necessarily NSs. (ii) Two consecutive strands that are not the strands n, 1 and which do not form an EJP are necessarily antiparallel. (iii) Assume that the JPs (i, i+1) and (j, j+1) form an interlock and neither of these JPs is (n, 1). Then the two loops i→i+1 and j→j+1 lie entirely in different planes, i.e. one loop lies in the front plane and the other lies in the back plane. Moreover, each of the pairs (i, j+1) and (j, i+1) consists of parallel strands and the strands of the one pair are antiparallel with the strands of the other pair. (iv) Two consecutive strands (in the same or in different sheets) cannot lie on different sides of an interlock. (v) Assume that i↦j is a path that does not contain a JP and also does not contain the strands n, 1. Then the number of strands in this path is odd (even) and the number of loops is even (odd) if and only if the strands i, j are parallel (antiparallel). Included in the parallel case (even number of loops) is the trivial path i↦i.

If the two consecutive strands are not n, 1 then (i) follows directly from fundamental principle 3. If the two consecutive strands are n, 1 and we accept the existence of at least one strand k between them, a systematic examination of all possible cases (regarding the location of other strands such as k−1, k+1 and paths such as 1↦k and k↦n) shows violation of fundamental principle 1 and/or fundamental principle 2. Hence (i) is valid for any pair of consecutive strands. Part (ii) follows directly from fundamental principle 3 since, otherwise, their loop would cross from one plane to the other. The two exceptions are allowed because n→1 is a fictitious loop or the loop of an EJP and these cases do not cause such violation. Part (iii) is a direct consequence of fundamental principle 3 and part (ii). Part (iv) follows immediately from part (iii), since the loop connecting the two consecutive strands would have to cross one of the loops of the interlock. Special consideration is needed for the cases where (i) the two consecutive strands on different sides of the interlock are n, 1 and (ii) one of the JPs of the interlock is (n, 1). In these cases, the presence of the fictitious loop does not cause a violation of fundamental principle 3. However, in these cases, the path 1↦n will have to contain both JPs of the interlock and this causes a violation of fundamental principle 1. Part (v) is a direct consequence of (ii), since all consecutive strands of the path are antiparallel and the number of strands equals the number of loops plus one. This argument fails if the path contains the consecutive strands n, 1. ▪

Under the assumption of proposition 4.1, a motif possesses the following properties: (i) two JPs (i, i+1) and (j, j+1) cannot have all the properties of an interlock except the property that (i, j) and (i+1, j+1) are NSs and (ii) there do not exist two JPs (i, i+1) and (j, j+1) such that i and j+1 lie in the same sheet, j and i+1 also lie in the same sheet, and if i is to the left (right) of j+1 then i+1 is to the right (left) of j.

For part (i), assume, for clarity, that i+1 and j+1 are not NSs, hence there exists a strand k between them, (i, i+1) is a front JP, (j, j+1) is a back JP, both are upward and i is to the left of j. All other cases can be treated in a similar way. Let (l, l+1) and (r, r+1), respectively, be the left and the right EJPs. Fundamental principle 1 implies that k belongs to either the rightward path l+1↦i or the leftward path r+1↦j. Both these cases must be rejected since they violate fundamental principle 2 and/or fundamental principle 3. Regarding part (ii), the difference with an interlock is that now one of the JPs is upward and the other is downward. Both JPs have the same direction, say rightward for clarity. Then the path must include the right EJP so that it can change direction from rightward to leftward and then it must contain a loop m→m+1 that crosses one or both of the JPs; this violates either part (i) or proposition 4.1(iv). ▪

Under the assumption of proposition 4.1, the IJPs appear only in the form of interlocks.

Let (i, i+1) be an IJP and, for clarity, assume that it is upward, in the front plane and rightward. All other cases can be treated in a similar way. The path i+1↦i has to include the right EJP so that it changes direction from rightward to leftward. Then it must cross from the right to the left of the IJP (i, i+1) and, by proposition 4.1(i), this may take place only with a JP (j, j+1), where j is to the left and j+1 is to the right of the IJP (i, i+1). By proposition 4.2(ii), the JP (j, j+1) is also upward. By proposition 4.2(i), i, j and i+1, j+1 must be NSs. Thus, the two JPs (i, i+1) and (j, j+1) form an interlock. Other JPs crossing the interlock cannot exist according to proposition 4.1(iv). ▪

5. Determination of all possible geometrical structures and all canonical motifs for sandwich proteins

We present a slight modification of the definition of a geometrical structure (Fokas et al. 2005) and introduce certain symmetries that geometrical structures may satisfy. We then construct systematically all possible geometrical structures and canonical motifs consisting of 6–10 strands. We use for geometrical structures the same terms used for motifs (e.g. jumping loop, JP, EJP, interlock and path), the only difference being that instead of strands we use strand positions.

A geometrical structure is an arrangement of strand positions (denoted by dots) that lie in two different levels (sheets) and each position is connected (by an undirected loop) with two different strand positions, so that the following rule is satisfied: a loop either connects two NS positions in the same sheet, or it is a jumping loop that forms an interlock with another jumping loop, or it is an edge loop.

An example of a geometrical structure with n=9 strand positions is shown in figure 4a.

Figure 4.

An example of a geometrical structure with two interlocks and n=9. (a) The geometrical structure and (c) the central part. (b) The left and (d) the right edge parts are shown.

For the creation of a sandwich protein, it is necessary that there exists at least one interlock. Furthermore, in all observed cases, the maximum number of strands in a path that lies entirely in the same sheet is four. Hence, we make the following two assumptions.

Each geometric structure contains at least one interlock.

Let M denote the number of strands in a path that lies entirely in the same sheet. Then M≤4.

It is convenient to decompose a geometrical structure into three basic components: the central part that consists of all interlocks and all paths between two neighbouring interlocks and the left and right edge paths that consist of the remaining strands and loops at the left and right of the central part, respectively. For example, for the geometrical structure of figure 4a, the central part (figure 4c) consists of two interlocks and two paths: one in the lower sheet, which is the trivial path consisting of the common position of the two interlocks and the other in the upper sheet consisting of one loop and the two strand positions of the left and right interlocks. The left edge part (figure 4b) consists of three loops (one loop being the left edge loop) and two strands at the lower sheet. The right edge part (figure 4d) consists of just the right edge loop since the two rightmost strand positions are included in the central part. This example shows that in some cases an edge part may consist of only an edge loop and no strand positions.

5.1 Representation of all edge parts

Any pair of the left and right edge parts is represented by an edge matrix

$$E=\left[\begin{array}{ll}{l}_1\hfill & r_1\hfill \\ l_2\hfill & r_2\hfill \end{array}\right],$$

where the entries of the left (right) column denote the number of strand positions of the left (right) edge part and the entries of the upper (lower) row denote the number of strands in the upper (lower) sheet. Thus, for example, l₂ and r₁ denote, respectively, the number of strands in the lower sheet of the left edge part and in the upper sheet of the right edge part. In the example of figure 4, l₁=0, l₂=2, r₁=0, r₂=0.

We say that a geometrical structure or the central part of a geometrical structure possesses the LR, or the UL, or the D symmetry, if each of its strand positions is symmetric to another strand position with respect to a vertical axis, or a horizontal axis, or a point. It turns out that any two of the above symmetries imply the third. Thus, we use the term ‘all’ if any two of them are valid. Also, we use the term none if none of these symmetries is valid. Also we say that a pair of the left and right edge parts has the LR, UL, D, all and none of the symmetry properties if, respectively, the left and right columns are the same (l₁=r₁, l₂=r₂), or the lower and upper rows are the same (l₁=l₂, r₁=r₂) or the diagonal entries are the same (l₁=r₂, l₂=r₁), or all entries are the same (l₁=l₂, r₁=r₂), or none of the above takes place. In the case that a geometrical structure possesses the LR or UL or D symmetry, we use the term ‘symmetry pair’ for two different symmetric positions. If the geometrical structure possesses all symmetry properties, then there are symmetry quadruplets, consisting of four different positions with the property that each of them forms a symmetry pair with each of the remaining three positions, one pair with respect to the LR, another with respect to the UL and the third with respect to the D symmetry. If the geometrical structure possesses the LR or all symmetry properties, then there may also exist up to two self-symmetric positions, i.e. positions that lie on the vertical symmetry axis. Examples are shown in figure 5.

Figure 5.

(a) LR, (b) UL, (c) D, (d) all and (e) none. Examples of geometrical structures with symmetry properties. The symmetry axes for the LR and UL properties are indicated with dashed lines and the symmetry point for the D property by ‘squares’. Positions denoted with ‘circles’ represent examples of symmetry pairs (LR, UL and D cases) and a symmetry quadruplet (‘all’ case). Self-symmetric positions are denoted with a star.

5.2 The generation of canonical motifs

According to Fokas et al. (2005) and Kister et al. (2006), each geometrical structure gives rise to canonical motifs, by placing the strands in specific strand positions and requiring the rule that two positions connected with a loop must be occupied by consecutive strands. Each position is connected by a loop with two other positions. Thus, after strand 1 is placed in any of the n positions, there are two available positions to place strand 2. After strand 2 is placed in one of these two positions, there is only one position available to successively place each of the remaining strands, since the other one is already occupied by the previous strand. Thus, after 1 and 2 are placed in a specific position, one canonical motif is generated. Since there are two choices to place strand 2 and n choices to place strand 1, the total number of canonical motifs generated is, in general, 2n. However, if the geometrical structure possesses a symmetry property, then there are cases where two canonical motifs coincide after one of them is properly rotated (i.e. if the left–right sides or the upper–lower sheets or both are interchanged). Hence, only one of them is counted. This leads to the following restrictions.

Restriction 1. If two geometrical structures coincide after an appropriate rotation then only one of them is used, since the other generates the same canonical motifs.

Restriction 2. If two central parts coincide after an appropriate rotation then only one of them is used, since they generate two geometrical structures for which restriction (1) applies.

Restriction 3. If a geometrical structure possesses one of the LR, UL, D (respectively, all) symmetries, then only one position from a symmetry pair (respectively, quadruplet) is used, since the other(s) will generate the same canonical motif.

Restriction 4. If strand 1 is placed in a self-symmetric position (which may exist if the geometrical structure possesses the LR or all symmetries) then strand 2 is placed in only one of the two available positions since the other will generate the same canonical motif.

Restriction 5. In the case of all symmetry properties with two self-symmetric positions (as in figure 4c), only one of these two positions is used to place strand 1, due to restriction 3.

5.3 Construction of all possible central parts

One way to systematically construct all possible central parts is to first consider the number of interlocks contained in each central part and then to analyse all possible cases of paths between two interlocks. Since n≤10, there exists only one central part with four interlocks (and no loops between them). Thus, all other central parts contain up to three interlocks. By definition 5.1, a path between two neighbouring interlocks lies entirely in the same sheet. This path may either consist of only one strand position, common to the two interlocks (trivial path), or, by assumption 5.3, it may contain up to two additional positions (up to three loops). Furthermore, if two central parts coincide, when properly rotated, then only one is counted, see restriction 2. A systematic construction leads to a total of only 16 central parts. Six of these central parts have already been observed and these cases are presented in figure 6, while the remaining 10 (presented in figure 7) have not been observed yet.

Figure 6.

All possible central parts observed in actual cases and their symmetry properties. (a) c=4 (all) (4a); (b) c=6 (all) (6a); (c) c=7 (LR) (7a); (d) c=8 (all) (8a); (e) c=8 (all) (8b); (f) c=9 (none) (9a).

Figure 7.

All possible cases of unobserved central parts with their symmetry properties. (a) c=8 (LR) (8a); (b) c=9 (LR) (9a); (c) c=9 (LR) (9b); (d) c=10 (all) (10a); (e) 10 (all) (10b); (f) 10 (LR) (10c); (g) 10 (none) (10d); (h) 10 (UL) (10e); (i) 10 (LR) (10f); (j) 10 (D) (10g).

5.4 Construction of all edge part pairs

Since a pair of edge parts is represented by an edge matrix, we construct all edge matrices. Restriction 1 implies that certain edge matrices are not eligible for a given central part that possesses some symmetry property. Specifically, consider the following four matrices:

$$E_1=\left[\begin{array}{cc}v& u\\ x& y\end{array}\right],E_2=\left[\begin{array}{cc}u& v\\ y& x\end{array}\right],E_3=\left[\begin{array}{cc}x& y\\ v& u\end{array}\right],E_4=\left[\begin{array}{cc}y& x\\ u& v\end{array}\right],$$

where any of them generates the other three if we interchange its columns, or rows or its diagonal entries. From the pairs (E₁, E₂), (E₁, E₃) and (E₁, E₄), only one of the two matrices is used if the central part possesses, respectively, the LR, UL, D symmetry properties. If the central part possesses all symmetry properties, only one of the above four matrices is used.

The strand positions that lie in the same sheet of an edge part belong to a path that also contains one strand position of the closest interlock. Then by assumption 5.3

$$0\le l_1,l_2,r_1,r_2\le 3.$$ (5.1)

Let e be the total number of strand positions of both edge parts, i.e.

$$e=l_1+l_2+r_1+r_2.$$ (5.2)

For each value of e, we determine all possible values of l₁, l₂, r₁, r₂ taking into account (5.1), (5.2) and the choices of E₁, E₂, E₃, E₄ as described above. The values of e are determined by e=n−c, where c is the number of strand positions of a central part. From figures 6 and 7, all possible values of c are 4, 6, 7, 8, 9 and 10. From 6≤n≤10, it follows that 0≤e≤6. Not all values of e are combined with all values of c; for example, the values e=5, 6 are combined only with c=4, while e=1 is combined only with c=6, 7, 8, 9. As an example, consider the case where the total number of strand positions of the left edge part is 5 (=l₁+l₂). Then the pairs (l₁,l₂)=(5,0), (4,1), (1,4), (0,5) are not valid and only the pairs (3,2), (2,3) may be used. Similarly, if the total number of strand positions of the right edge part is 6 (=r₁+r₂), only the pair (r₁, r₂)=(3,3) may be used. As another example consider the case where the value e=2 is combined with the central part 4a of figure 6 thus giving a geometrical structure with n=2+4=6 positions. Since this central part has all symmetry properties, only the following four edge matrices are eligible:

$$\left[\begin{array}{cc}2& 0\\ 0& 0\end{array}\right],\left[\begin{array}{cc}1& 0\\ 1& 0\end{array}\right],\left[\begin{array}{cc}1& 1\\ 0& 0\end{array}\right],\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right].$$

It follows that this combination produces only four geometrical structures, which have the same symmetry property with the above edge matrices, i.e. none, UL, LR and D, respectively. These four geometrical structures are:

A substructure of a central part (hence also of a geometrical structure that contains this central part) is called uneven, if it consists of two consecutive interlocks and of two paths between them, such that one of the two paths has an odd number of loops and the other path has an even number of loops (including the case of zero loops). The end strand positions of an uneven substructure are the positions at the two ends of it, i.e. the two leftmost positions of its left interlock and the two rightmost positions of its right interlock. The internal positions are the remaining ones.

All possible uneven substructures appear in the central parts 7a 9a (figure 6) and 9b, 9c, 10f and 10g (figure 7). Note that the central parts 7a (figure 6) and 9b, 9c (figure 7) coincide with their uneven substructures. The central parts 10f, 10g of figure 7 are composed of two uneven substructures of the form 7a (one of them is rotated in the case of 10f), which have a common interlock, the central one.

If strand 1 is placed at an end position of an uneven substructure U, then strand 2 may not be placed in an internal position of U.

If strand 2 is placed in an internal position, then strand n may not occupy an internal position and the fictitious loop n→1 will not belong to U. Then, by proposition 4.1(v) and definition 5.6, the two rightmost strands of the left interlock or the two leftmost strands of the right interlock would be antiparallel, which contradicts proposition 4.1(iii). ▪

Let m be the number of canonical motifs generated by a geometrical structure. (i) Assume that a geometrical structure does not contain an uneven substructure. If this geometrical structure possesses the LR, or the UL or the D symmetry, then m=n. If it has all or none of these symmetries then, respectively, m=n/2 or m=2n. (ii) Assume that the geometrical structure does contain one uneven substructure U with u strand positions. If this geometrical structure possesses none of the symmetry properties then m=2u−4. If it possesses the LR or D property then m=u−2. (iii) If the geometrical structure does contain two uneven substructures then m=2.

(i) If the geometrical structure possesses none of the symmetry properties, then, after strand 1 is placed in each of the n positions, strand 2 may be placed in any of the two available positions, thus producing m=2n canonical motifs. If the geometrical structure possesses one of the symmetry properties then n=2p+s, where p is the number of pairs of symmetric positions and s is the number of positions that are self-symmetric. In the UL, D case s=0. In the LR case, restriction 4 implies that after strand 1 is placed in each of the s positions then strand 2 may be placed in only one of the two available positions. Thus, there are two canonical motifs generated by each of the p positions and one canonical motif generated by each of the s positions, for a total of m=2p+s=n canonical motifs. In the case of all symmetries n=4q+s, where q is the number of symmetry quadruplets; s is the number of self-symmetric positions; and s=0 or s=2. Restriction 3 implies that only one of the four positions of a quadruplet is used, each generating two canonical motifs. Restrictions 4 and 5 imply that the number of canonical motifs generated by the s self-symmetric positions is s/2, for s=0 or s=2. Hence, the number of canonical motifs is m=2q+s/2=n/4. (ii) By lemma 5.7, each of the four end positions generates one canonical motif and each of the remaining u−4 internal positions generates two canonical motifs each, for a total of m=4+2(u−4)=2u−4 canonical motifs. The UL property is not valid due to the existence of an uneven substructure U, thus only LR and D may be valid. If in addition the geometrical structure possesses one of these properties, then U also possesses the same property and u=2p+s, where p is the number of symmetry pairs of U and s is the number of its self-symmetric positions (which may exist only in the LR case). By restriction 4, the s positions generate one canonical motif each. By restriction 3, only p of the 2p positions are used. These include two end positions each generating only one canonical motif, by lemma 5.7. The remaining p−2 positions generate two canonical motifs each. Thus, the total number of canonical motifs is m=2(p−2)+2+s=u−2. (iii) If the geometrical structure contains two uneven substructures, then n≤10 implies that it consists of three interlocks and the two paths between two interlocks in each substructure have 0 and 1 loop, respectively (cases 10f, 10g of figure 7). In this case, the central part consists of these two substructures, the total number of strand positions is 10 and the edge parts consist of only the edge loops. The resulting geometrical structure possesses either the LR (case 10f) or the D (case 10g) symmetry. By lemma 5.7, n→1 must belong to both uneven substructures, i.e. it must be a jumping loop of the central interlock. The LR or D symmetry of the geometrical structure implies that strand 1 may be placed in only two of the four positions of the central interlock and, by lemma 5.7, strand 2 may not be placed in an internal position. Thus, one canonical motif is generated in each case for a total of m=2 canonical motifs. ▪

All possible geometrical structures, their symmetry properties and the number m of canonical motifs generated by each geometrical structure are presented in tables 1a and 1b for the observed central parts and in table 2 for the unobserved ones. Recall that e+c=n, where c and e denote, respectively, the number of strand positions of the central part and the pair of the edge parts. In the left column of each sub-table, the values e, c (first row) and the central part with its symmetry property (second row) are shown. The symmetry properties of the resulting geometrical structure follow from the fact that a geometrical structure possesses a symmetry property (LR or UL or D or all) if both its central part and the representative edge matrix possess the same property. Thus, for example, if the central part possesses all properties (hence also the LR property) and the edge matrix possesses the LR property, then the geometrical structure also possesses the LR property. In the remaining columns, the applicable edge matrix is shown in the top row and the symmetry property of the resulting geometrical structure is shown in the bottom row, together with the number m of canonical motifs generated by this geometrical structure, as implied by theorem 5.8. Following are some examples that illustrate the results contained in these tables.

Table 1(a).

All possible geometrical structures for the observed central parts, for n=6,7,8,9, with their symmetry properties and the number m of canonical motifs they generate.

Table 1(b).

All possible geometrical structures for the observed central parts, for n=10, with their symmetry properties and the number m of canonical motifs they generate.

Table 2.

All possible geometrical structures for the unobserved central parts with their symmetry properties and the number m of canonical motifs they generate.

For n=6 (table 1a) and the sub-table with e=0, c=6, the only geometrical structure is generated by the combination of the central part 6a of figure 6 and the two edge parts with zero strand positions, i.e. containing only an edge loop. The geometrical structure and the m=3 canonical motifs are

Only one position (denoted by ‘○’) is used from the symmetry quadruplet that consists of four end positions and only one of the two self-symmetric positions is used (denoted by a star), since these two positions constitute a UL symmetry pair. The ‘○’ position generates the first two canonical motifs and the ‘star’ generates the third one. All other canonical motifs, which are generated if strands 1 and 2 are placed in positions other than the above, coincide with the above three after appropriate rotation. In the sub-table with e=2, c=4, the 4 geometrical structures generated are:

There are no self-symmetric positions and all positions denoted by ‘○’ generate two canonical motifs each, thus m=12 in the ‘none’ and m=6 in the other three cases. For example, the canonical motifs for the UL case are as follows:

$$\begin{array}{ccc}\text{1}& \text{2}& \text{4}\\ \text{6}& \text{5}& \text{3}\end{array}\begin{array}{ccc}\text{1}& \text{6}& \text{4}\\ \text{2}& \text{3}& \text{5}\end{array}\begin{array}{ccc}6& 1& 3\\ 5& 4& 2\end{array}\begin{array}{ccc}2& 1& 5\\ 3& 4& 6\end{array}\begin{array}{ccc}4& 3& 1\\ 5& 6& 2\end{array}\begin{array}{ccc}4& 5& 1\\ 3& 2& 6\end{array}$$

For n=9 (table 1a) and the sub-table with e=2, c=7, all geometrical structures contain the central part 7a of figure 6, which is an uneven substructure. Hence n→1 must belong to this central part. Consider the first and last geometrical structures (columns 2 and 8):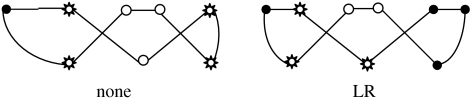

If strand 1 is placed in one of the end positions of the uneven substructure, then strand 2 cannot be placed in any of the internal positions, thus in each such case only one canonical motif is generated. For example, if strand 1 is placed in the upper left of the end positions, the canonical motifs generated in the none and LR cases are

$$\begin{array}{cccccc}3& 2& 1& 5& 6& 8\\ 4& 9& 7& & & \end{array}\begin{array}{cccccc}2& 1& 4& 5& 8& 7\\ 3& 9& 6& & & \end{array}.$$

If strand 1 is placed in one of the three internal positions, then strand 2 may be placed in each of the two available positions with one exception for the LR case: if strand 1 is placed in the self-symmetric position, then strand 2 may be placed in only one of the two available positions. Thus, the total number of canonical motifs generated is 10 for the none and 7 for the LR cases.

For n=10 (table 2) and the sub-table with e=0, c=10, the geometrical structure of the seventh row, which uses the central part 10f of figure 7, contains two uneven substructures:

The loop n→1 must belong to both uneven substructures, hence it lies in their common (central) interlock. Since the geometrical structure possesses the LR property, there are two positions to place strand 1, denoted by a star. For each of them, n must occupy a position of the interlock, hence only the following two canonical motifs are generated:

$$\begin{array}{cccccc}4& 2& 1& 6& 7& 9\\ 3& 5& 10& 8& & \end{array}\begin{array}{cccccc}2& 4& 5& 10& 9& 7\\ 3& 1& 6& 8& & \end{array}.$$

A summary of the number of geometrical structures and the total number of motifs, for each n, is presented in table 3.

Table 3.

The total number of geometrical structures (g.s.) and canonical motifs for each n.

	n=6	n=7	n=8	n=9	n=10
g.s.	5	7	19	49	63
c.m	33	89	200	625	825

6. Conclusions

Without using the results of the present work, the a priori number of all possible motifs is prohibitively large. Specifically, all possible subsets of k and (n−k) strands, belonging to two different sheets, are $(\begin{array}{c}n\\ k\end{array})$ All possible permutations for each set of k and (n−k) strands are, respectively, k! and (n−k)! Thus, the number of all motifs with k and (n−k) strands in the two sheets is $k!\times (n-k)!\times (\begin{array}{c}n\\ k\end{array})=n!$ for each value of k. If we assume that there must be at least two strands in each sheet, then k=2, …, (n−2), hence the total number of motifs for given n is (n−3)×n! Thus, if we do not use the results of the present work, the total number of all possible motifs is the sum of these numbers for n=6, 7, 8, 9, 10, which is approximately equal to 32 million motifs. Even if we use the convention of this paper that two motifs are considered the same if they coincide after an appropriate rotation, we find about one-quarter of the above number of motifs, i.e. approximately 7 million motifs, which is still prohibitively large. Our approach has led to a tremendous reduction of the number of (canonical) motifs, namely table 3 gives only 143 geometrical structures and 1772 motifs!

Some of the rules used here are consistent with the stereochemical approach based on the construction of structural trees (Efimov 1997). Our analysis is restricted only to sandwich proteins, and, for this case, our results are more complete and yield an effective characterization of the relevant motifs.