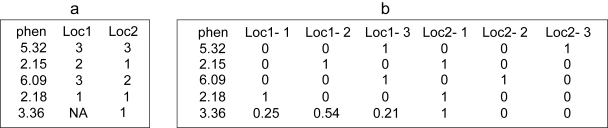
Figure 1. Illustration of data formatting.

Part a provides an example of a data set in which the genotypes of individals are fully known (or, alternatively, totally unknown and considered as missing data); 1 and 3 stand for the homozygotes (e.g. ‘AA’ and ‘aa’) and 2 for the hererozygote. Part b illustrates a second kind of data set in which the genotypes are defined by their probabilites. In this example, part b is the exact equivalent of part a (and then, the frequency of the ‘known’ genotypes is always 1), but in practice, especially when the data result from a Haley-Knott regression, the probabilities, computed from the genotypes at flanking markers, may be intermediate. Missing values (‘NA’) are allowed in type a data sets, and are replaced by genotypic probabilities equal to genotypic frequencies in the rest of the population (here, close to 0.25, 0.5, and 0.25 since the population is an F₂). The Z matrix used for the regression (equation 5) is computed from a ‘type b’ data set, meaning that if ‘type a’ data is provided, it is turned into ‘type b’ before the genetic regression.