Refinement of non-calorimetric determination of the change in heat capacity, ΔCp, of protein unfolding and validation across a wide temperature range

Abstract

The change in heat capacity, ΔC_p, upon protein unfolding has been usually determined by calorimetry. A non-calorimetric method which employs the Gibbs-Helmholtz relationship to determine ΔC_p has seen some use. Generally, the free energy change upon unfolding of the protein is determined at a variety of temperatures and the temperature at which ΔG is zero, T_m, and change in enthalpy at T_m are determined by thermal denaturation and ΔC_p is then calculated using the Gibbs-Helmholtz equation. We show here that an abbreviated method with stability determinations at just two temperatures gives values of ΔC_p consistent with values from free energy change upon unfolding determination at a much wider range of temperatures. Further, even the free energy change upon unfolding from a single solvent denaturation at the proper temperature, when coupled with the melting temperature, T_m, and the van’t Hoff enthalpy, ΔH_vH, from a thermal denaturation, gives a reasonable estimate of ΔC_p, albeit with greater uncertainty than solvent denaturations at two temperatures. We also find that non-linear regression of the Gibbs-Helmholtz equation as a function of stability and temperature while simultaneously fitting ΔC_p, T_m, and ΔH_vH gives values for the last two parameters that are in excellent agreement with experimental values.

Introduction

One of the more interesting aspects of the thermodynamics of proteins is the non-zero values of the change in heat capacity (ΔC_p) upon unfolding. The change in heat capacity (ΔC_p) upon denaturation can be determined directly by calorimetric methods, but this requires large amounts of protein and specialized equipment. Pace and Laurents¹ introduced a non-calorimetric method using a combination of solvent and thermal denaturation derived stability data in the Gibbs-Helmholtz equation to calculate the ΔC_p for the unfolding of ribonuclease T1 and ribonuclease A. Pace and Makhatadze² determined the ΔC_p for the unfolding of ribonuclease A using differential scanning calorimetry and found that the non-calorimetric method gave very similar results. This non-calorimetric method has since seen successful application to a variety of proteins, but several questions remained.

In large part because of the length of time required to achieve equilibrium at low temperatures, Pace and Laurents examined only a fairly narrow temperature range from 19 to 29 °C. One possible criticism is that data collected over a wider temperature range might give a different result for ΔC_p. Automated equipment developed in our laboratory^3,4 makes it relatively easy for us to conduct solvent denaturations with long equilibration times. Further, Pace and Laurents calculated ΔC_p at different temperatures and averaged them or fitted the curve of stability versus temperature to the Gibbs-Helmholtz equation by manual adjustment of the value of ΔC_p, less practical than non-linear regression over a wide temperature range. Non-linear regression also offers the possibility of calculating the melting temperature, T_m, and the van’t Hoff enthalpy, ΔH_vH, and comparing these values derived from ΔG as a function of temperature to those obtained experimentally from a thermal denaturation as a validation of the procedure. Lastly, while several wild-type proteins and a few mutants have been examined, a large series of mutant proteins has never been examined. Therefore, we decided to determine the free energy change upon unfolding, which, in interest of conciseness, we will usually refer as stability, over a wide range of temperatures for wild-type staphylococcal nuclease and 22 mutant proteins in order to determine ΔC_p.

Materials and Methods

Mutagenesis, Protein Expression, and Protein Purification

The construction, expression and purification of the mutants of staphylococcal nuclease used in this study has been described elsewhere.^5–8 Briefly, a set of single, double, triple, quadruple and multiple mutants were previously constructed to include every possible permutation of leucine, isoleucine and valine at two overlapping sets of four positions (23/25/66/72, 66/72/92/99) in the core of staphylococcal nuclease. In most cases new preparations of protein were made and found to give results consistent with earlier work. We selected all 16 possible quadruple mutants at 23/25/66/72. Because this set generally has values of m_GuHCl below that of wild-type nuclease, we also selected 6 additional mutants from the 66/72/92/99 set which had values of m_GuHCl equal to or greater than wild-type. The melting temperature (T_m) of most mutants were at or above 40 °C, thus providing a relatively wide temperature range at which free energy change upon unfolding could be reliably determined.

Thermal Denaturation and Data Analysis

The thermally-induced unfolding of nuclease was monitored by probing the changes in intrinsic fluorescence of the protein as a function of temperature. The experiments were carried out as previously described.^3,4,9 Wild-type staphylococcal nuclease has been thermally denatured 42 times and the values used here are the previously reported averages.⁹

Guanidine Hydrochloride Denaturation and Data Analysis

The stabilities of the mutants were determined by guanidine hydrochloride denaturation in an AVIV model ATF-101 fluorometer as previously described.^3,4 The guanidine hydrochloride solution (6M GuHCl, 100 mM NaCl, 25mM sodium phosphate, pH 7.0) used in these experiments was prepared with extreme caution to maintain the concentration and pH. Note that this is slightly different from earlier work in the Stites laboratory, with the inclusion of sodium chloride in the guanidine hydrochloride solution. Data analysis was carried out assuming a two-state model for reversible protein unfolding. This data analysis yields three parameters: the stability difference in the absence of denaturant between a protein’s native and denatured states (ΔGH₂O), the rate of change of free energy with respect to guanidinium hydrochloride (GuHCl) concentration (m_GuHCl or d(ΔG)/d[GuHCl]), and the concentration of GuHCl at which the protein is half denatured (C_m).

Isothermal guanidine hydrochloride-induced unfolding experiments were carried out, at 4, 10, 15, 20, 30, and 40 °C for mutants and 3, 10, 15, 20, 25, 30, 40, and 50 °C for wild-type. In solvent titration experiments at or above 15 °C, a 5–8 minute equilibration time period was required between two additions. This time period allowed for proper equilibration of the native and denatured states. Occasional longer intervals in each denaturation were used to confirm that sufficient time was allowed for equilibration. However at 10°C or lower, the equilibration time interval had to be increased to 20 minutes. During denaturation experiments at lower temperatures, the equilibration time interval at a data point near C_m was increased to 35 minutes. This allowed us to confirm that 20 minutes was sufficient to reach equilibrium. In order to prevent condensation on the walls of the cuvette at lower temperatures (4 °C and 10 °C), a slow stream of liquid nitrogen boil off at low pressure was used. At higher temperatures (30 °C and 40 °C) noise problems were encountered due to the formation of bubbles on the cuvette wall. To avoid bubbles, the buffer was degassed by raising the temperature to about 5 °C above the experimental temperature for 10 minutes. The cuvette was then removed from the holder and gently tapped to dislodge the bubbles. The temperature was lowered to the desired experimental value and the protein stock solution was added. The sample was covered with a small plastic lid to prevent evaporation. All the quadruple mutants were previously characterized by guanidine hydrochloride denaturations⁷ at 20 °C, but were redetermined as part of this study so that all thermal and guanidine hydrochloride denaturations were measured using protein from a single preparation.

Non-linear regression analysis

The free energy difference between native and denatured states obtained from guanidine hydrochloride denaturation experiments at various temperatures and mid-point temperature and van’t Hoff enthalpy obtained from thermal denaturation experiments were fit to the Gibbs-Helmholtz equation (Eq. 1) using non-linear regression. SigmaPlot (versions 9.01 or 10) was used for the non-linear regression analysis and various starting values were tested to ensure that the algorithm converged to a common value.

$$\mathrm{\Delta }\text{G}=\mathrm{\Delta }{\text{H}}_{\text{vH}}(1-\frac{\text{T}}{{\text{T}}_{\text{m}}})-\mathrm{\Delta }{\text{C}}_{\text{p}}({\text{T}}_{\text{m}}-\text{T}+\text{T}ln\frac{\text{T}}{{\text{T}}_{\text{m}}})$$ (Eq. 1)

In the Gibbs-Helmholtz equation T_m (midpoint temperature or melting temperature) is the temperature at which half the protein molecules are unfolded. ΔH_vH is the van’t Hoff enthalpy at the melting temperature and ΔC_p is the change in heat capacity upon protein unfolding. The assumption is made that ΔC_p is not a function of temperature.

By rearranging the Gibbs-Helmholtz equation (Eq. 1) we obtain Eq. 2 from which ΔC_p can be calculated by substituting the values of ΔH_vH and T_m from thermal data and ΔG is ΔGH₂O from solvent denaturation data.

$$\mathrm{\Delta }{\text{C}}_{\text{p}}=\frac{\mathrm{\Delta }\text{H}\left(1-\frac{\text{T}}{{\text{T}}_{\text{m}}}\right)-\mathrm{\Delta }\text{G}}{{\text{T}}_{\text{m}}-\text{T}+\text{T}ln\left(\frac{\text{T}}{{\text{T}}_{\text{m}}}\right)}$$ (Eq. 2)

The non-linear regression analysis on each mutant was done in four different ways:

• The mid-point temperature T_m and van’t Hoff enthalpy ΔH obtained from thermal denaturation experiments were defined. A non-linear regression of ΔG_calc (predicted values) against ΔGH₂O (experimental values) was performed while fitting only ΔC_p.

• ΔH was defined experimentally and regression of ΔG_calc against ΔGH₂O was done while fitting the values of T_m and ΔC_p.

• T_m was defined experimentally and regression of ΔG_calc against ΔGH₂O was done while fitting the values of ΔH and ΔC_p.

• None of the thermodynamic parameters were defined and a non-linear regression of ΔG_calc against ΔGH₂O was carried out while the values of ΔH, T_m and ΔC_p were all allowed to fit.

Further, non-linear regression was first done against all the stabilities obtained over the entire temperature range, and then just with stabilities determined at 15 and 20°C, and just with stabilities determined at 20 and 30°C.

Regression was done for the mutant proteins using only a single stability value at each temperature, that being the most recently obtained, if more than one was available. However for wild-type, to which all mutants are referred, we used all available data, including 106 independent determinations of free energy change upon unfolding at 20°C.

Results

Previously our laboratory constructed a large set of conservative packing mutants to include every possible permutation of leucine, isoleucine, and valine at two overlapping sets of four positions (23/25/66/72, 66/72/92/99) in the core of staphylococcal nuclease.^5–8 A subset of 22 quadruple mutants⁷ was chosen for this present study. The selected mutants had melting temperatures (T_m) at or above 40°C, thus providing a relatively wide temperature range over which free energy change upon unfolding could be determined.

Each of the 22 mutants, along with wild type nuclease, was characterized by thermal denaturation experiments using the fluorescence of Trp140 as a probe of structure, as described elsewhere.³ During the original work on these mutants, thermal denaturations had previously been obtained (J. Chen and W. E. Stites, unpublished observations). Thermal and guanidine hydrochloride denaturations were performed again so that all thermal and guanidine hydrochloride denaturations were measured using protein from a single preparation. Stabilities reported here are the same as those previously reported within the range of expected experimental error. Table I includes the midpoint temperatures, T_m, and van’t Hoff enthalpies, ΔH_vH, newly obtained.

The free energy difference (ΔGH₂O) between the native state and denatured state is the measure of protein stability determined from guanidine hydrochloride denaturation experiments. Each of the 22 mutants was previously characterized by guanidine hydrochloride at 20°C⁷ but stability at this temperature was determined again, as well as at 4, 10, 15, 20, 30, and 40°C. Stabilities reported here are the same as those previously reported within range of expected experimental error. The values of ΔGH₂O, the midpoint concentration, C_m, and the rate of change of ΔG with respect to guanidine hydrochloride concentration, or slope value, m_GuHCl at all the temperatures examined are available in supplementary material online.

Non-linear regression analysis was used to fit ΔG values predicted by the Gibbs-Helmholtz equation to various experimentally determined ΔGH₂O values obtained at different temperatures. The stabilities of wild-type and five representative mutants are depicted as a function of temperature in Figure 1. As shown in Table I, by defining or fitting different combinations of thermodynamic parameters, four different values of ΔC_p were obtained by non-linear regression analysis as described in Materials and Methods. The value of ΔC_p obtained by defining T_m and ΔH_vH as values obtained experimentally in thermal denaturation while using all the stabilities at all temperatures is referred to as the global value and is shown in the first column. In the second and third columns, respectively, are the experimentally determined values of T_m and ΔH_vH. In the fourth and fifth columns are the fitted values of ΔC_p and ΔH_vH when T_m is defined as the value experimentally determined. Similarly, in the sixth and seventh columns are the fitted values of ΔC_p and T_m when ΔH_vH is defined as the value experimentally determined. Finally, the last three columns are those values obtained by allowing ΔC_p, ΔH_vH, and T_m all to simultaneously vary when fitting the ΔG values predicted by the Gibbs-Helmholtz equation to experimentally determined ΔGH₂O values.

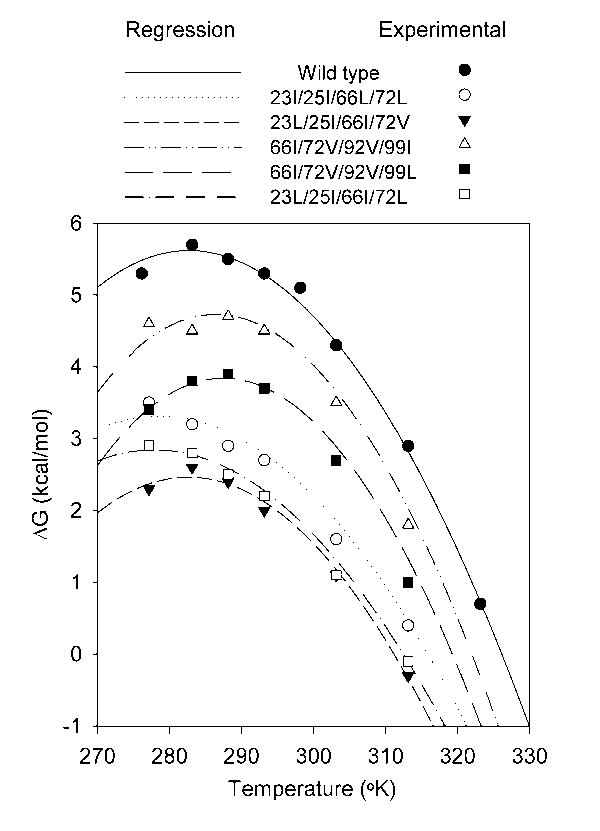
Figure 1.

Plot of ΔGH₂O against temperature for wild-type staphylococcal nuclease and five representative quadruple mutants. The mutant 23I/25I/66L/72L was chosen as it has a low ΔC_p and subjectively amongst the worst fits. The mutant 23L/25I/66I/72V has a markedly lower stability than wild-type, yet has a ΔC_p that is nearly the same and a subjectively good fit. The mutants 66I/72V/92V/99I and 66I/72V/92V/99L are poor and good fits respectively but both with high ΔC_p. The mutant 23L/25I/66I/72L has a low ΔC_p and a good fit. The lines are the best fit against the Gibbs-Helmholtz equation obtained by non-linear regression of predicted ΔG against ΔGH₂O for all measured temperatures while defining T_m and ΔH as the values obtained from thermal denaturation experiments. The points indicate experimental data obtained at various temperatures. The standard deviation in ΔGH₂O found in repeated determinations of wild-type stability at 20°C is ± 0.1 kcal/mol.

Discussion

Comparison of ΔC_p values with and without fixed, experimental ΔH and T_m values

One of the strengths of using non-linear regression to fit the Gibbs-Helmholtz equation to stabilities determined at different temperatures is that it is possible to supply fixed, experimental values for ΔH and T_m, or to fit ΔH, T_m, or both along with ΔC_p. This gives an excellent idea of the robustness of the fitting procedure and the possible degree of error. In Figure 2A it is obvious that allowing T_m to float has little impact on the value of ΔC_p.

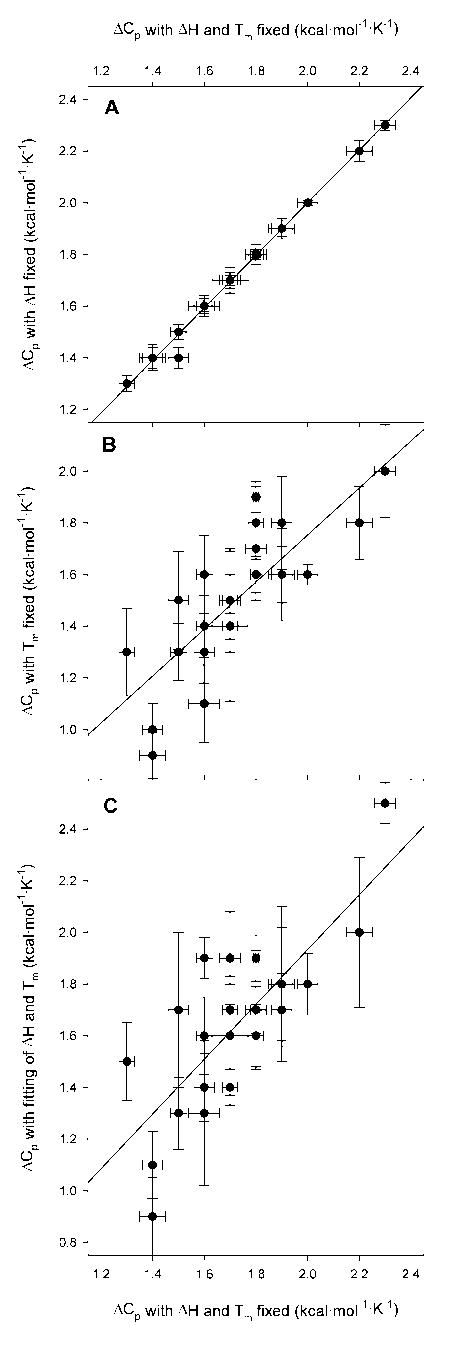
Figure 2.

Comparison of ΔC_p values with and without fixed, experimental ΔH and T_m values. In all panels the x axis is the global ΔC_p. This is the value of ΔC_p obtained by fitting predicted ΔG against ΔGH₂O for all measured temperatures while defining T_m and ΔH as the values obtained from thermal denaturation experiments. In panel A, the global ΔC_p is plotted against the value of ΔC_p returned by the regression when ΔH is fixed as the experimental value obtained from thermal denaturation and T_m is fit as well. In panel B, the global ΔC_p is plotted against the value of ΔC_p found by the regression when T_m is fixed as the value obtained from thermal denaturation and ΔH is now fit. In panel C, the global ΔC_p is plotted against the value of ΔC_p returned when ΔC_p, ΔH, and T_m are all fit by non-linear regression at once. In all cases, the error bars are those given by the regression and the lines are the least square regression of ΔC_p versus ΔC_p.

The value of ΔC_p is much more dependent upon the value of ΔH, as illustrated in panels 2B and 2C. The value of ΔH is a much more informative constraint on fitting than is T_m. There is much less agreement between the value of ΔC_p with ΔH defined as the experimental value and the value when ΔH is allowed to float. Although the overall fit is better when both ΔC_p and ΔH are allowed to vary, the error estimate returned by the regression program for ΔC_p dramatically increases. This is again due to the fact that the values of ΔC_p and ΔH are tightly coupled. While larger than the error when ΔH is defined, these errors, on the order of ± 0.2 kcal/(mol·K), compare favorably with the ± 0.5 kcal/(mol·K) estimated for calorimetrically determined ΔC_p.

Comparison of fitted ΔH and T_m values with experimental values

When both ΔC_p and T_m are fitted by non-linear regression the regression values are very similar to the experimental values, as shown in Figure 3A. Even when all three variables in the Gibbs-Helmholtz equation, ΔC_p, ΔH and T_m, are fit simultaneously the values of T_m hardly diverge from the experimental values (Figure 3B). The melting temperature, T_m, for nuclease is experimentally quite well defined in the thermal denaturation experiment, with an error of only ± 0.4°, so there is little to be gained from obtaining it via regression. Further, it is quite reassuring to see that the regression returns, within experimental error, the same value, meaning that the curve of ΔGH₂O versus temperature defines T_m quite well.

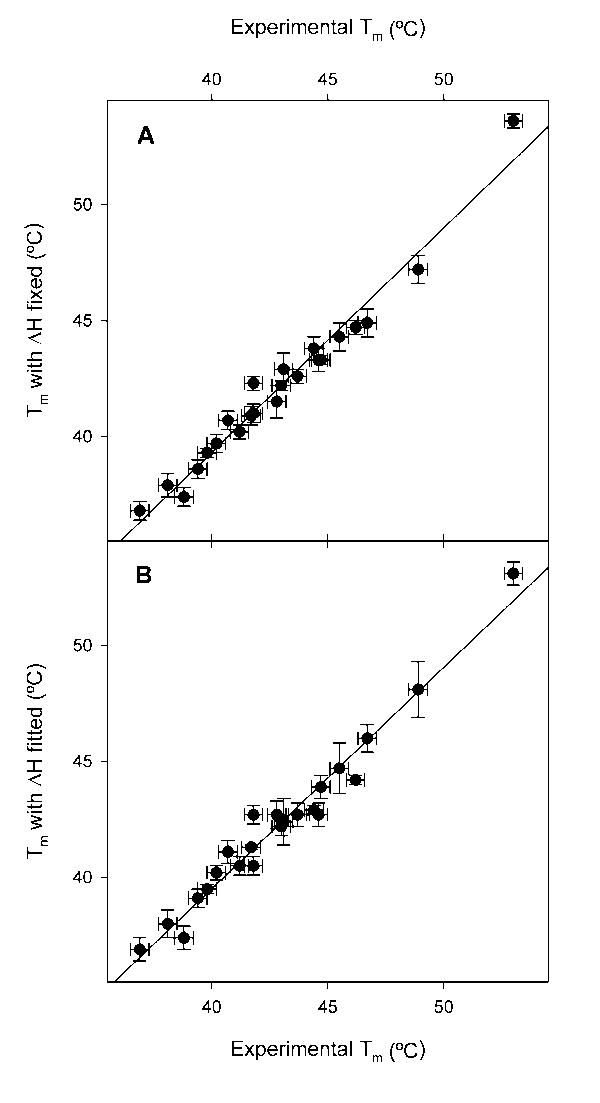
Figure 3.

Comparison of experimental T_m values to those derived from non-linear regression. In both panels the x axis is the experimental T_m. In panel A, the experimental T_m is plotted against the value of T_m returned by the regression when ΔH is fixed as the value obtained from thermal denaturation while ΔC_p is fit as well. In panel B, the experimental T_m is plotted against the value of T_m returned when ΔC_p, ΔH, and T_m are all fit by non-linear regression at once. The error bars in the y axis are those given by the regressions, the error in the x axis is the ± 0.4° standard deviation found in repeated thermal denaturations of wild-type staphylococcal nuclease.⁹ The lines are the least square regression of T_m versus T_m.

When both ΔC_p and ΔH are fitted while T_m is fixed at the experimental value, ΔH does not usually vary more than the amount of the experimental error. However, close inspection of Figure 4A reveals that the experimental values at the low end of the range tend to be greater than those returned by regression as evidenced by the greater slope of the least squares regression of experimental ΔH versus regression ΔH.

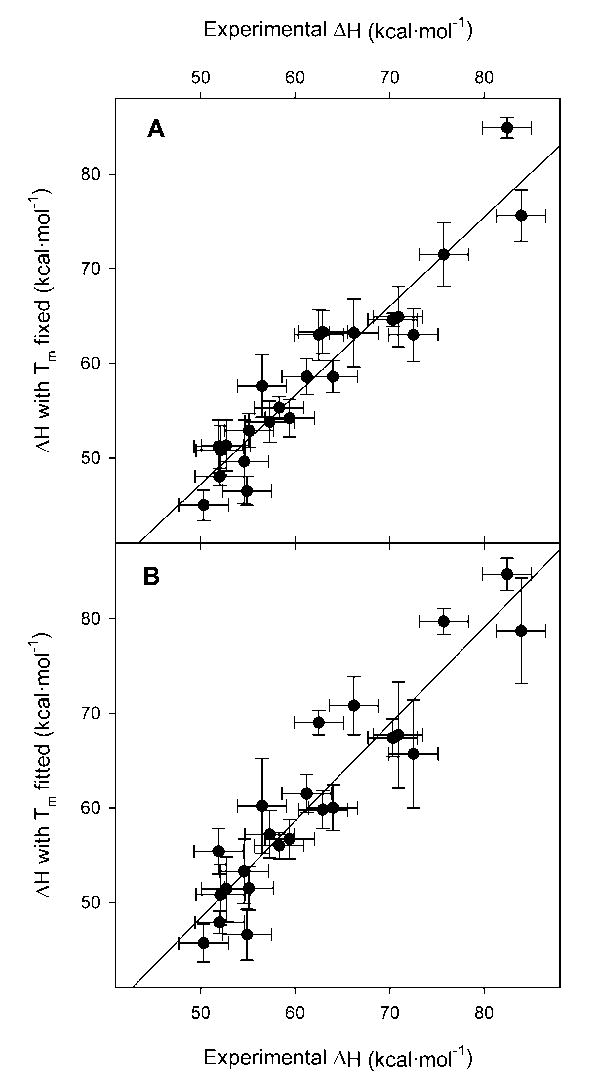
Figure 4.

Comparison of experimental ΔH values to those derived from non-linear regression. In both panels the x axis is the experimental ΔH. In panel A, the experimental ΔH is plotted against the value of ΔH returned by the regression when T_m is fixed as the value obtained from thermal denaturation while ΔC_p is fit as well. In panel B, the experimental ΔH is plotted against the value of ΔH returned when ΔC_p, ΔH, and T_m are all fit simultaneously by non-linear regression. The error bars in the y axis are those given by the regressions, the error in the x axis is the ± 2.6 kcal/mol standard deviation found in repeated thermal denaturations of wild-type staphylococcal nuclease.⁹ The lines are the least square regression of ΔH versus ΔH.

Comparison of ΔC_p values using stability determined at different temperatures

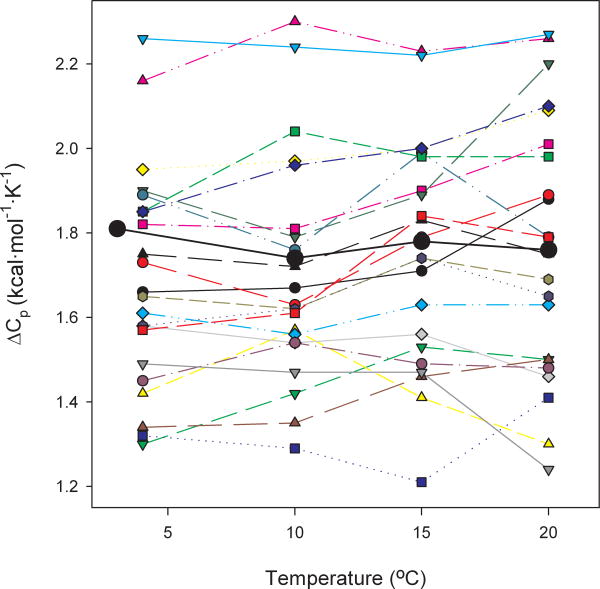
As the curves of stability versus temperature in Figure 1 show, there is good agreement of the predicted ΔG with the observed ΔGH₂O over the entire temperature range accessible to us. In other words, the assumption that ΔC_p is independent of temperature seems valid. Of course ΔC_p may be calculated at a given temperature using the particular free energy difference between the folded and unfolded states determined at that temperature and the experimental values of ΔH and T_m. Generally, up to 20° there is little variation with temperature, as is demonstrated in Figure 5 where such temperature-particular ΔC_p values are graphed as a function of temperature. As Pace and Laurents¹ pointed out, any error in ΔG translates into a larger error in ΔC_p as the T_m is neared. At 40°C, near the melting point of many of the mutants, a change in ΔG of 0.1 kcal/mol translates into a change in calculated ΔC_p of as much as 10 or 20 kcal/(mol·K), therefore we do not show single temperature ΔC_p values at these higher temperatures. The ΔC_p values calculated at 20°C are shown in Table II while all the values calculated at each temperature, including higher temperatures not shown in Figure 5, are available in the online supplementary material.

Figure 5.

Plot of ΔC_p versus temperature for all 22 mutants and wild-type. Each ΔC_p value is calculated from the experimental ΔH and T_m and the ΔGH₂O for that protein at each temperature.

In addition to calculating ΔC_p based on a single solvent denaturation and a single thermal denaturation, it is possible to use fewer stabilities in the non-linear regression. The point that error in ΔG translates into a larger error in ΔC_p as the T_m is neared means that the values of ΔG near T_m have less informational content and, indeed, their inclusion may be counterproductive. The curvature of ΔG with temperature is greatest near the temperature of maximal stability and this curvature is dictated by ΔC_p. Accordingly, we repeated the non-linear regression using the experimentally defined T_m and ΔH, but used only the ΔGH₂O data determined at 15 and 20°C, and then again using only the stabilities at 20 and 30°C. These values are given in Table II to the level of precision estimated by the regression program.

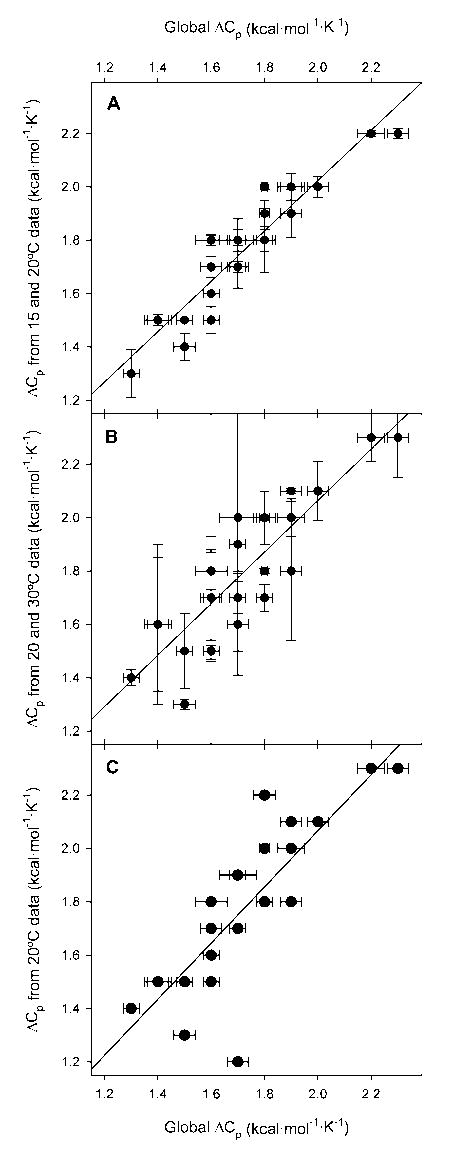
In Figure 6 we plot, after rounding to a more realistic single decimal place, the ΔC_p values calculated from these more limited data sets to that calculated from the global dataset. The agreement is quite good in general. A linear regression of dependent variable ΔC_p from the fit to the 15 and 20°C data against the independent variable, ΔC_p from the global fit, gives a standard error for the 15 and 20°C ΔC_p of ± 0.1 kcal/(mol·K). Similarly, the standard error in the ΔC_p from the 20 and 30°C data was ± 0.1 kcal/(mol·K). Interestingly, linear regression of ΔC_p values calculated solely from the 20°C data against the global ΔC_p values gives a standard error that is higher, but still a quite respectable ± 0.2 kcal/(mol·K). Of course, the independent variable has error in it, estimated at ± 0.2 kcal/(mol·K). The error in either the ΔC_p from the fit to the 15 and 20°C data or the ΔC_p from the 20 and 30°C data is the same, (0.2² + 0.1²)^1/2 = 0.22, which rounds to ± 0.2 kcal/(mol·K). The error in ΔC_p calculated from the 20°C data is slightly greater, (0.2² + 0.2²)^1/2 = 0.28, which rounds to ± 0.3 kcal/(mol·K).

Figure 6.

Comparison of ΔC_p values calculated with ΔGH₂O values determined at different temperatures and the values of ΔH and T_m from a thermal denaturation. In all panels the x axis is the global ΔC_p. This is the value of ΔC_p obtained by fitting predicted ΔG against ΔGH₂O for all measured temperatures while defining T_m and ΔH as the values obtained from thermal denaturation experiments. In panel A, the global ΔC_p is plotted against the value of ΔC_p returned by the regression against just the stabilities determined at 15 and 20°C. In panel B, the global ΔC_p is plotted against the value of ΔC_p returned by the regression against just the stabilities determined at 20 and 30°C. In panel C, the global ΔC_p is plotted against the value of ΔC_p calculated from just the stability determined at 20°C. In all cases, the error bars are those given by the regression and the lines are the least square regression of ΔC_p versus ΔC_p.

What is the error in the value of ΔC_p? In various tables and graphs we give the standard error estimates returned from the non-linear regression. This estimate is best understood as the range of values that give a similar degree of fit of the predicted ΔG from the Gibbs-Helmholtz equation to the experimental ΔGH₂O values. In particular for the global fit, this error (an average ± 0.04 kcal/(mol·K)) is artificially low since it does not take into account the possible error in ΔH and T_m. When all thermodynamic parameters, ΔC_p, ΔH, and T_m, are simultaneously fit the error estimates returned for T_m (an average ± 0.5°) and ΔH (an average ± 2.8 kcal/mol) are very similar to the experimental errors for wild-type (T_m ± 0.4°, ΔH ± 2.6 kcal/mol) that we have verified by long experience.⁹ This implies that the error estimates for ΔC_p in this case are reasonable, although even at an average ± 0.2 kcal/(mol·K) this is still excellent for this notoriously difficult to measure parameter.

This should not be interpreted as implying that the values returned when ΔC_p, ΔH, and T_m are all simultaneously fit are more accurate. ΔGiven the high degree of autocorrelation of ΔC_p and ΔH it is clear that providing a good value for ΔH will greatly increase the accuracy of ΔC_p. Rather, the precision of the regression when providing experimental values for ΔH and T_m is clearly incorrect and the true precision (error) is better reflected in the simultaneous fit. To acknowledge this fact, in Table I we limit the number of significant digits.

Finally our data clearly show that there is no need to routinely make measurements over a wide temperature range. This is because the stabilities taken at lower temperatures have a much greater impact on the value of ΔC_p than the high temperature data. Therefore measuring ΔGH₂O within 10 or even 15° of T_m does little to improve the accuracy of ΔC_p, although it does improve values of T_m if one wishes to determine that by non-linear regression. On the other hand, accurate determination of ΔC_p does not require extreme low temperature data. Indeed, the global fit is likely to be less accurate than a fit using a more limited temperature range. It was extremely difficult to collect good data at 10° and below. Problems with condensation, ensuring adequate equilibration times, and the increased chances of misadventure in a data collection that takes nearly a complete day not only required many data sets to be recollected but also lead to us to believe that there is a much greater chance that stabilities determined at low temperature have greater potential for error and, of course, error here translates into large errors in ΔC_p.

Comparison with wild-type ΔC_p literature values

Our value of ΔC_p for wild-type staphylococcal nuclease of 1.8 kcal/(mol·K) agrees well with literature values. The ΔC_p of wild type nuclease was first determined using differential scanning calorimetry (DSC) by Griko et al.,¹⁰ although they used a variant with seven additional disordered amino acids at the N-terminus. They found that in 10 mM sodium acetate, 100 mM NaCl the value of ΔC_p was 1.8 kcal/(mol·K), with no error estimated. DSC done by Tanaka et al. found a value of 2.2 kcal/(mol·K), again with no error estimate given, in various buffers at 50 mM and 100 mM NaCl.¹¹ Also using DSC, Carra and Privalov measured ΔC_p as 2.1 ± 0.5 kcal/(mol·K) in 20 mM sodium phosphate, 100 mM NaCl, 1mM EDTA at pH 7.0.¹²

Eftink and Ramsay¹³ estimated a ΔC_p value of 2.27 ± 0.15 kcal/(mol·K) for the unfolding of wild-type nuclease in 10 mM TrisHCl, 100 mM NaCl, pH 7.0. They used a different non-calorimetric approach, carrying out a non-linear fit of the Gibbs-Helmholtz equation to two state stability calculated from thermal unfolding followed by fluorescence and CD at 222 and 235 nm as probes of structure. In essence, this approach determines ΔC_p as the second derivative of ΔG versus temperature. They fit all three datasets globally, which gave the value listed above, as well as separately to obtain very similar results.

Lasalle et al.¹⁴ used a non-calorimetric method somewhat comparable to that used here to calculate a value for nuclease’s ΔC_p of 3.1 ± 0.5 kcal/(mol·K). In this work the protein was unfolded using pressure at various temperatures over the range of 1.5 to 35°C using NMR as a probe of structure in D₂O, 20 mM Mes at pH 5.3. While ΔC_p can vary with pH, little change for the ΔC_p of nuclease occurs in the pH range of 5–7¹² so the offered explanation¹⁴ for this high value and an elevated protein stability is the fact that the stabilities were determined in D₂O.

As of yet, there is no calorimetric ΔC_p available for the mutants of staphylococcal nuclease examined here. One of the interesting questions about the denaturation of nuclease is whether it proceeds by a two state model (used here in the data analysis) or via some intermediate. The first evidence that a two state model might be insufficient was the V66W mutant.¹⁵ Bolen’s group has argued convincingly^16,17 that neither a simple two or three state model fully explains the data for wild-type nuclease and the majority of mutants that have been studied. They generally favor the variable two state model proposed by Shortle,^18,19 wherein the character of the denatured state changes with mutation, denaturant concentration, or temperature. Carra and Privalov, proponents of the three state model for solvent denaturation,²⁰ have concluded that thermal denaturation of wild-type nuclease is two state.^12,20 On the other hand, Eftink’s group has shown that V66W mutant with tryptophan or tryptophan analogues, appears to be better fit by a three state thermal unfolding model.²¹ Maki et al.^22,23 showed that a proline-minus variant of nuclease could have no more than 5% of an equilibrium intermediate at any urea concentration, while a F76W mutant of this proline-minus variant has nearly 50% of the protein populating an equilibrium intermediate at moderate urea concentrations. We have recently published data showing that the thermal denaturations of wild-type nuclease and ninety-seven single mutants are identical within experimental error, whether followed by Trp 140 fluorescence or circular dichroism helical signal at 222 nm, putting rather strict limits on the amount of helix that might be present in any putative intermediate.⁹ The NMR used to measure structure in the ΔC_p determination just noted above clearly shows that the C-terminal helix breaks down ahead of the core of the protein, but this is regarded by these workers as a structural fluctuation of the native state.¹⁴ Therefore, another reason for elevated ΔC_p in this work may be that the two states for which the change in heat capacity is measured may be different from those measured by Trp 140 fluorescence.

While the calorimetric and non-calorimetric values for wild-type agree well, in the longer term, we hope to measure ΔC_p for these mutants calorimetrically. The agreement, or lack thereof, between the calorimetric values and the non-calorimetric values presented here will provide useful evidence for determination of the appropriate model for nuclease denaturation.

Conclusion

It is clear for staphylococcal nuclease that ΔGH₂O values determined at two or even a single temperature, when coupled with ΔH_vH and T_m from a thermal denaturation, give values for ΔC_p consistent with ΔGH₂O values measured over a much wider temperature range. This validates the use of fewer temperatures, making this approach more experimentally practical. Indeed, not only is the use of fewer temperature more practical, it is superior. The best non-calorimetric values for ΔC_p are those fitted by regression against stabilities determined at 15 and 20°C, with a likely error of ± 0.2 kcal/(mol·K). Even ΔC_p calculated from the T_m and ΔH_vH derived from thermal denaturation and a single ΔGH₂O value determined at a temperature near the point of maximal stability is reasonably accurate, with an error of ± 0.3 kcal/(mol·K). Although the exact temperature ranges over which the procedure should be done will vary from protein to protein, a similar approach should work with most proteins that undergo reversible thermal and solvent denaturation. In future communications we will further explore the implications of the ΔC_p values we have found in staphylococcal nuclease and the correlation it shows with m_GuHCl.