Resampling methods for improved wavelet-based multiple hypothesis testing of parametric maps in functional MRI

Abstract

Two- or three-dimensional wavelet transforms have been considered as a basis for multiple hypothesis testing of parametric maps derived from functional magnetic resonance imaging (fMRI) experiments. Most of the previous approaches have assumed that the noise variance is equally distributed across levels of the transform. Here we show that this assumption is unrealistic; fMRI parameter maps typically have more similarity to a 1/f-type spatial covariance with greater variance in 2D wavelxet coefficients representing lower spatial frequencies, or coarser spatial features, in the maps. To address this issue we resample the fMRI time series data in the wavelet domain (using a 1D discrete wavelet transform [DWT]) to produce a set of permuted parametric maps that are decomposed (using a 2D DWT) to estimate level-specific variances of the 2D wavelet coefficients under the null hypothesis. These resampling-based estimates of the “wavelet variance spectrum” are substituted in a Bayesian bivariate shrinkage operator to denoise the observed 2D wavelet coefficients, which are then inverted to reconstitute the observed, denoised map in the spatial domain. Multiple hypothesis testing controlling the false discovery rate in the observed, denoised maps then proceeds in the spatial domain, using thresholds derived from an independent set of permuted, denoised maps. We show empirically that this more realistic, resampling-based algorithm for wavelet-based denoising and multiple hypothesis testing has good Type I error control and can detect experimentally engendered signals in data acquired during auditory-linguistic processing.

Introduction

In analysis of functional magnetic resonance imaging (fMRI) data, the usual strategy is massively univariate testing to identify significantly activated voxels by thresholding the voxel-wise test statistics in a way which controls the false positive error rate at some acceptable level given the large number of tests involved (typically N ~ 20,000 for whole brain statistical mapping). A classical threshold for multiple comparisons is the Bonferroni-corrected voxel-wise P-value, which controls the family-wise error rate (FWER) but is conservative for correlated tests and lacks power. A more recently introduced alternative threshold is defined in terms of controlling the false discovery rate (FDR), which is less conservative than the Bonferroni correction and easily generalised to correlated tests.

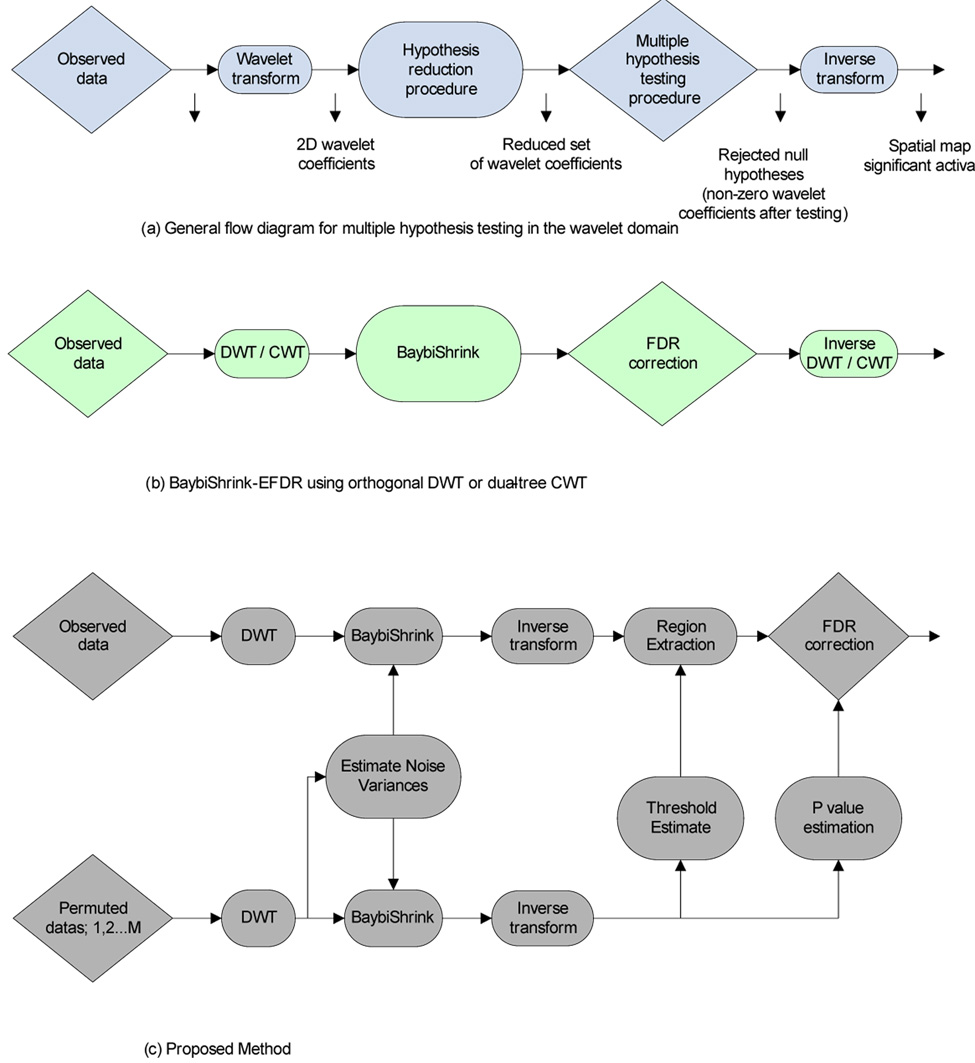
Further improvements in power could be achieved by reducing the number of univariate tests and the wavelet transform has been considered as a suitable mathematical basis for this purpose. The discrete wavelet transform (DWT) has a property of data compaction; that is, the energy of a signal tends to be concentrated in a few large wavelet coefficients while the energy of the noise is more evenly distributed across a larger number of much smaller coefficients. Univariate testing over a small number of large wavelet coefficients has therefore been advocated as a way of reducing the search volume or number of tests required for whole brain mapping; see Fig. 1a for a general schematic of a two-stage wavelet-based algorithm for multiple hypothesis testing.

Figure 1.

Schematics of two-stage wavelet-based hypothesis testing algorithms. Top row: Schematic of general approach. Middle row: BaybiShrink-EFDR algorithm. The total number of hypotheses to be tested is first reduced by a preliminary shrinkage operation in the wavelet domain; then the smaller subset of surviving coefficients is tested, one hypothesis at a time, in a way which controls the FWER (or the FDR) over all tests. Finally, the signal is reconstructed in the spatial domain by the inverse DWT using only those coefficients which survive both tests (all other coefficients being set to zero). Bottom row: BaybiShrink denoising of 2D wavelet coefficients is informed by resampling-based estimates of the spectrum of noise variance at different spatial scales. Permuted maps are additionally used to estimate the preliminary threshold τ_s used to define a restricted set of voxels in the spatial domain and to estimate the P-values for each voxel in this set prior to a final stage of multiple hypothesis testing controlling the false discovery rate.

Ruttimann et al (1998) made the first effort to apply this two stage operation to the problem of multiple hypothesis testing in the analysis of fMRI statistic maps. They used an omnibus χ ² test on all coefficients in each level of the 2D DWT to identify which levels represented signals, and then individually tested each coefficient in those levels against a Bonferroni-corrected threshold. Shen et al (2002) recently introduced an analogous method, called the enhanced false discovery rate (EFDR) algorithm. In the first stage of their procedure, the generalized degrees of freedom (Ye, 1998) is used to define the reduced subset of wavelet coefficients for further testing and, in the second stage, they tested the significance of statistics informed by the local neighborhood around each wavelet coefficient (rather than treating each coefficient in isolation), setting the significance threshold for each test such that the FDR was controlled at a certain level. Sendur et al (2005) developed and validated an alternative algorithm, called BaybiShrink-EFDR, in the same general framework; see Fig.1b. The main idea was to use a Bayesian bivariate shrinkage algorithm to define a reduced set of coefficients at the first stage and then to test all surviving coefficients using a normal approximation and an FDR-corrected threshold. Additionally, the authors showed that performance of this algorithm was superior on the basis of a complex (dual-tree) wavelet transform compared to an orthogonal DWT; Fig. 1c.

Although these and other wavelet-based methods for multiple hypothesis mapping of fMRI data have greater statistical power than more conventional methods for testing a larger number of voxel statistics in the spatial domain (Fadili and Bullmore, 2004), all variations on this two-stage testing theme so far described share two important disadvantages. First, since the hypothesis testing is done in the wavelet domain, these procedures lack interpretability of statistical significance in the spatial domain. Second, they make an important but simplistic assumption; namely, the decorrelating properties of the wavelet transform are such that the noise variance is evenly distributed as white Gaussian noise across all scales of the 2D- or 3D-DWT applied to a map of voxel statistics. Thus it has been assumed (following Ruttimann et al [1998]) that a reasonable estimate of the noise variance at all scales or levels of the transform can be obtained from the mean absolute deviation (MAD) of the wavelet coefficients in the finest (highest frequency) scale. However, it is well-known that spatial maps of voxel statistics estimated by analysis of fMRI time series have a non-Gaussian covariance, and some research has addressed this issue Turkheimer et al, 2003; Van De Ville et al, 2004) exploiting the decorrelating property of wavelets without assuming white Gaussian noise. In fact, spatial maps of responses in fMRI are smooth and (as we show below) the noise is disproportionately represented in the coefficients of the DWT representing low frequency features in the maps.

The main innovation introduced in this paper is to improve the data fidelity of statistical testing in the wavelet domain by using resampling methods both to estimate the noise variance at each level of the wavelet transform, and to compute the critical values corresponding to probability thresholds for significance testing. The paper is structured as follows. First, we describe how activation statistic maps are generated from experimental and permuted fMRI time series data. Then we demonstrate how white Gaussian fields and smoother fields of test statistics are represented by the spectrum of variances of wavelet coefficients at different levels of the DWT; and thus that the wavelet variance spectrum of fMRI statistic maps under the null hypothesis is not compatible with the critical assumption of white Gaussian noise equally distributed across all levels. Third, we rehearse the BaybiShrink algorithm already described and show how it can be refined to incorporate noise variance estimates and critical values for significance testing in the spatial domain based on resampling of the observed fMRI time series in the wavelet domain (Bullmore et al., 2001). Finally, the methods are illustratively applied to simulated and experimental fMRI datasets to demonstrate nominal Type I error control and to provide preliminary evidence of favourable sensitivity compared to an alternative algorithm for non-parametric significance testing in the spatial domain.

Materials and methods

Experimental and permuted activation statistic maps

The experimental data were acquired during performance of a language processing task and have been extensively reported in the context of the Functional Image Analysis Contest, full details of which are described in Dehaene-Lambertz et al (2006). Briefly, this experiment involved auditory presentation of familiar or novel sentences spoken by familiar or novel speakers in a blocked periodic paradigm and was intended to activate perisylvian brain regions activated by processing novel and familiar linguistic material.

Functional MRI datasets acquired from 15 healthy volunteers during performance of this task were pre-processed individually, e.g., to correct effects of involuntary head motion, before a general linear model was fitted to the time series at each voxel. The design matrix comprised an orthogonal set of regressors representing the average difference in brain activation between language processing and baseline conditions, the activation difference between novel and familiar sentences, the activation difference between novel and familiar speakers, and the interaction between effects of speakers and sentences. Each regressor was convolved with a canonical hemodynamic response function before the model parameters were estimated by least squares. This time series regression analysis resulted in a set of four experimental activation statistic maps in the spatial domain (one for each regressor) for each of the 15 subjects. These observed spatial maps were co-registered in the standard space of Talairach (Talairach and Tournoux, 1988) and the median activation statistic for each regressor was estimated at each voxel; see Suckling et al (2006) for a complete description of these procedures.

We used a wavelet-based resampling or “wavestrapping” procedure to generate spatial maps of the same set of activation statistics under the null hypothesis (Bullmore et al, 2004). To do this, each pre-processed fMRI time series was decomposed using the 1-dimensional DWT, the wavelet coefficients at each level of the transform were randomly permuted, then the inverse transform was used to reconstitute the resampled data as a time series. This operation, repeated with the same permutation scheme identically at each voxel in an individual image, preserves the spatial and temporal covariance properties of the image but disrupts the relationship in time between task related components of variance and the presentation of experimental trials (Bullmore et al 2004). Activation statistics were estimated for each permuted time series, as described above for the observed time series, resulting in a set of four permuted spatial maps for each subject. The permuted statistic maps for all individuals were co-registered in standard space, and the median activation statistic was computed at each voxel, exactly as described for the observed maps. No spatial smoothing was applied to experimental or permuted activation statistic maps at any stage in their processing.

Wavelet representations of spatial and temporal noises

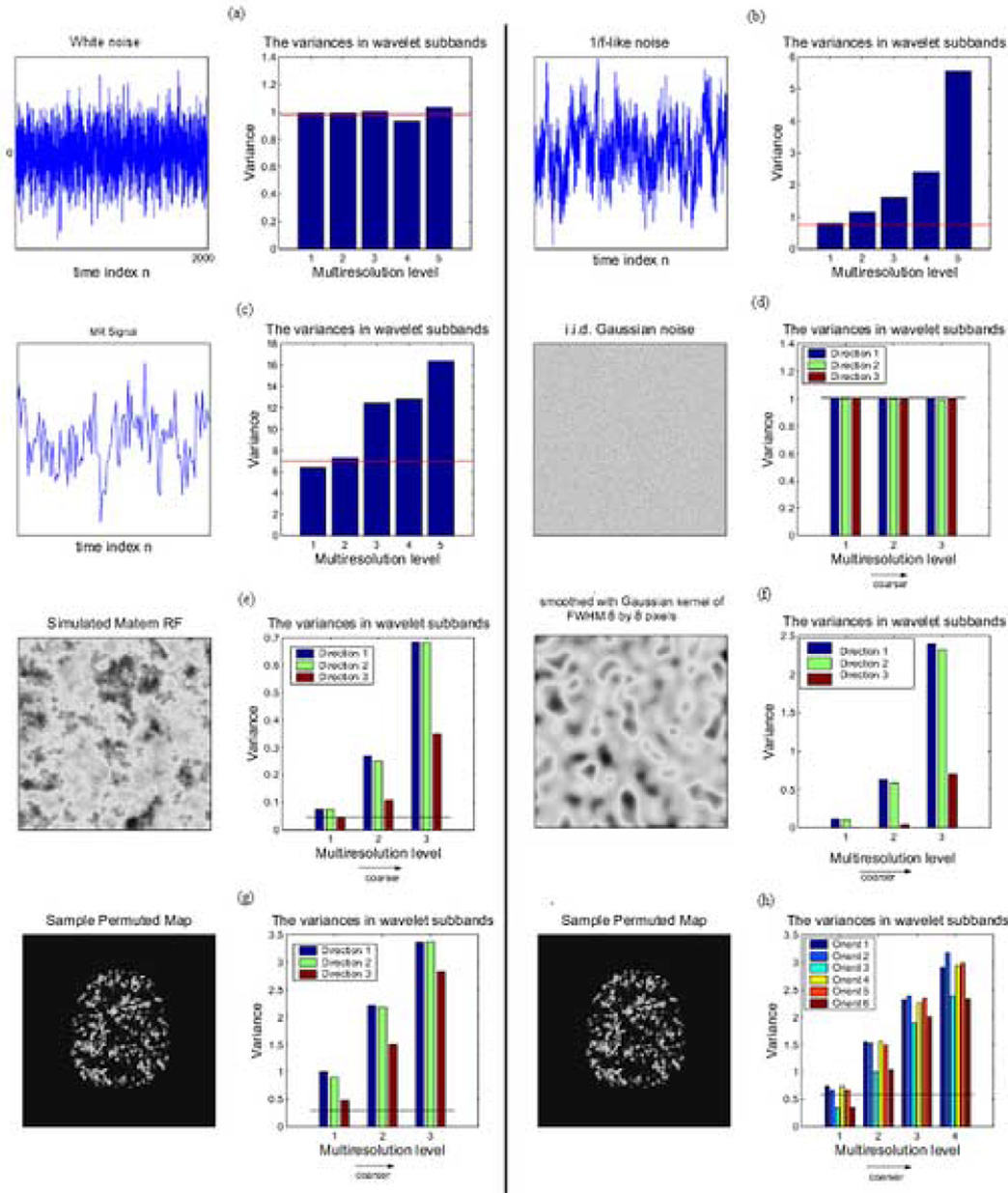
If we take the discrete wavelet transform of an independent and identically distributed (IID) one-dimensional process, we can see that the variance of the wavelet coefficients at each scale of the transform is approximately equivalent (Fig. 2a). In other words, the variance spectrum of the wavelet coefficients is flat across scales of the DWT. Hence, the variance of the coefficients at any scale of the DWT is reasonably well estimated by the median absolute deviation (MAD) of the coefficients at the finest scale (Donoho and Johnstone, 1994).

Figure 2.

Gaussian and non-Gaussian spatial (2D) and temporal (1D) signals and their corresponding wavelet variance spectra. a) 1D white noise has a flat wavelet variance spectrum where the variance at each scale is well approximated by an estimator based on the median absolute deviation (MAD) of the finest scale wavelet coefficients. b) Simulated 1D 1/f signal shows greater variance of the wavelet coefficients representing lower frequency trends in the time series, which is not well approximated by the MAD-based estimator. c) A functional MRI time series, acquired from a subject “at rest” (without experimental stimulation), has a wavelet variance spectrum similar to simulated 1D 1/f noise. d) A 2D spatial process with white Gaussian covariance has a flat 2D wavelet variance spectrum, i.e., the variances at all scales and orientations of the DWT are well approximated by the MAD-based estimator. e) A simulated Matern class spatial process and f) a smoothed Gaussian random field both have a wavelet variance spectrum with greater varainces of coefficients representing coarser scale spatial features. g) A permuted fMRI parameter map has greater variance of discrete wavelet transform coefficients, and h) complex wavelet transform coefficients, representing coarser scale spatial features, which is not well approximated by the MAD-based variance estimator (shown as a solid red line in all panels).

If we apply the same analysis to a simulated one-dimensional signal with 1/f-type spectral properties, in which low frequency trends are strongly represented, there is disproportionately large variance of wavelet coefficients at coarser scales of the DWT and this is substantially under-estimated by the MAD of the coefficients at the finest scale of the transform (Fig 2b). As an aside, note that fMRI time series are typically 1/f-type processes (Zarahn et al, 1997) and their wavelet variance spectrum is correspondingly dominated by the larger variances of coefficients at coarser scales (Fig. 2c).

Similarly for 2D processes, the wavelet spectrum is flat for coefficients of the 2D DWT applied to a Gaussian field of white noise (Wu et al, 1998; Pesquet et al, 1999), and the variance at all levels is reasonably well-estimated by the MAD of coefficients at the finest scale as illustrated by Fig.2d. However, for fields such as a Matérn class process (Whitcher, 2006), Fig 2e, or smoothed white Gaussian field, Fig. 2f, the variance spectrum of the wavelet coefficients is not flat. Rather there is disproportionately large variance of coefficients in the coarser scales of the transform that is not well estimated by the MAD of coefficients at the finest scale of the transform.

Importantly, it is clear by inspection of the permuted activation statistic maps that the spatial distribution of test statistics estimated in fMRI data under the null hypothesis is not white, i.e., the wavelet variance spectrum is not flat but is dominated by larger variances at coarser scales (Fig. 2g and 2h). This observation is consistent whether we consider the coefficients estimated by the orthogonal DWT (Fig. 2g) or a dual-tree complex wavelet transform (Fig. 2h). This is a significant observation because it indicates that any wavelet-based hypothesis-testing algorithm using the MAD of the finest scale coefficients as an estimator of the variance at all scales of the transform will substantially under-estimate the variance of coefficients at coarser scales under the null hypothesis, thereby potentially leading to erroneous rejection of the null hypothesis when testing coarse scale coefficients.

BaybiShrink-EFDR and related algorithms for multiple hypothesis testing

We previously described a two-stage procedure for multiple hypothesis testing in the wavelet domain (summarised schematically in Fig. 1). In the first stage of this algorithm, the complex wavelet coefficients of a 2D spatial map of fMRI activation statistics were denoised using a Bayesian bivariate shrinkage (BaybiShrink) operator detailed in Table 1. The BaybiShrink operator is basically a nonlinear function designed to exploit the generally expected dependencies between wavelet coefficients representing natural images. Let wavelet coefficient w₂ represent the parent of w₁, i.e., w₂ is the coefficient at the same location as w₁ , but at the immediately coarser scale, and assume that y₁ and y₂ are the noisy observations corresponding to wavelet coefficients w₁ and w₂ respectively. The Bayesian bivariate shrinkage function can be written as follows

$${\widehat{w}}_1=\frac{{(\sqrt{y_1^2+y_2^2}-\sqrt{3}{\sigma }_n^2/\sigma )}_{+}}{\sqrt{y_1^2+y_2^2}}\times y_1$$ (1)

where ${\sigma }_v^2$ and σ² are the noise and signal variances respectively, and ${\tau }_{\omega }\equiv \sqrt{3}{\sigma }_n^2/\sigma$ can be interpreted as a threshold value. Here (g)₊ is defined as

$${(g)}_{+}=\{\begin{array}{cc}0& \text{if}g<0\\ g& \text{otherwise}.\end{array}$$ (2)

Table 1.

Summary of the main steps of the algorithm for multiple hypothesis testing in the spatial domain after denoising in the wavelet domain; see also Fig 1.

1.	Compute the 2D DWT cofficients of a set of 10 permuted parametric maps derived from repeated wavelet resampling of a functional MRI dataset
2.	Combine the coefficients corresponding to the same level and orientation of the 2D DWT and store these as the empirical null data.
3.	Extract the coefficients corresponding to a specific level and orientation from the empirical null data. Estimate the corresponding variance and designate it as the noise variance, σn(li),corresponding to level li. Repeat the procedure for every level and orientation of the decomposition.
4.	BaybiShrink Denoising Algorithm : For each 2D DWT coefficient of the observed map,
	•	Estimate the noisy signal variance σ̂y using neighboring coefficients $${\widehat{\sigma }}_y^2=\frac{1}{M}{\displaystyle \sum _{y_{\iota }\in \mathrm{N}(k)}{y}_{\iota }^2}$$
	•	Estimate the signal variance σ̂ using $\widehat{\sigma }=\sqrt{{({\widehat{\sigma }}_y^2-{\widehat{\sigma }}_n^2(l_{\iota }))}_{+},}$
	•	Estimate the threshold value using ${\tau }_w={\widehat{\sigma }}_n^2(l_i)/\widehat{\sigma }$.
	•	Estimate each coefficient using Eqn. (1) with the estimated threshold value.
5.	Invert the denoised coefficients to obtain the denoised observed maps.
6.	Generate a new set of permuted parametric maps by fMRI time series resampling, repeat steps (1)–(4) and invert the DWT. Select a percentile value and compute the threshold value τs.
7.	Define a subset of voxels for significance testing by thresholding the denoised observed maps with the threshold value, τs, computed in the previous step.
8.	Compute the P-values for each of the voxels surviving step (7) using a permutation distribution of voxel statistics derived from the second set of permuted maps. Select an appropriate false discovery rate, αFDR, and apply the FDR procedure to control Type I error in observed maps.

To estimate the noise variance ${\sigma }_n^2$ from the noisy wavelet coefficients, the median absolute deviation (MAD) of the finest scale wavelet coefficients (HH₁ sub-band) has often been proposed as a convenient option:

$${\widehat{\sigma }}_n^2=\frac{\mathit{\text{median}}(|y_l|)}{0.6745},y_l\in \text{sub-band}H{H}_1.$$ (3)

To estimate the signal variance for each coefficient, we first estimate the noisy signal variance σ̂_y as follows:

$${\widehat{\sigma }}_y^2=\frac{1}{M}{\displaystyle \sum _{y_{\iota }\in \mathrm{N}(\kappa )}{y}_{\iota }^2}$$

where M is the size of a rectangular neighborhood N(k) of coefficients centered on the index coefficient. Then we can derive the signal variance $\widehat{\sigma }=\sqrt{{({\widehat{\sigma }}_y^2-{\widehat{\sigma }}_n^2(l_{\iota }))}_{+}.}$

In the second stage of this algorithm, we tested the denoised coefficients against a normal approximation using a multiple testing procedure designed to control the FDR and set all non-significant coefficients to zero. Finally, the inverse transform was used to reconstruct an activation map in the spatial domain.

In this note, we introduce two substantive changes to this algorithm. First, we replace the MAD estimator of variance, based only on the finest-scale wavelet coefficients of the experimental maps, with a more realistic, level-specific estimator of the noise variance σ_n , which is adaptive to the greater variance of coefficients representing low spatial frequencies. Second, we adopt a procedure similar to that previously described by Van de Ville et al (2004) to conduct the final tests of statistical significance in the spatial domain rather than the wavelet domain.

Data resampling to estimate wavelet coefficient variances

The permuted maps of activation statistics generated by wavelet-resampling of the experimental fMRI time series are used to estimate the variances of the wavelet coefficients at each level separately under the null hypothesis. The level-specific or sub-band adaptive estimates of the noise variance estimated in this way, denoted ${\widehat{\sigma }}_n^2(j)$ for the jth level of the wavelet transform, are then substituted into the BaybiShrink threshold ${\tau }_w={\widehat{\sigma }}_n^2(j)/\widehat{\sigma }$ to denoise the coefficients at the jth level. This refinement eliminates the need to use the MAD estimator of σ_n, which, as we have shown empirically above, will underestimate the variance of coarse scale coefficients unless the spatial covariance of the statistic maps is white. We apply the BaybiShrink operation, with level-specific estimates of the wavelet coefficient variances, to the coefficients generated by the complex wavelet transform (CWT) of both the experimental and permuted statistic maps. This procedure is summarized in Fig. 1.

Hypothesis-testing in a reduced search volume of the spatial maps

Once the wavelet coefficients have been denoised, we use the inverse transform to recover a continuous representation in the spatial domain of activation strength throughout the brain. We can then threshold this activation surface to identify the brain regions associated with the strongest signal. The choice of threshold for this purpose has often been defined heuristically. However, we can continue to exploit the information provided by the resampled data to make this choice more empirically driven. For example, we can find the 95th percentile value of the activation surface in the permuted data and apply this as a threshold τ_s to the activation surface in the experimental data. This operation considerably reduces the size of the search volume in the activated data before the final stage of testing.

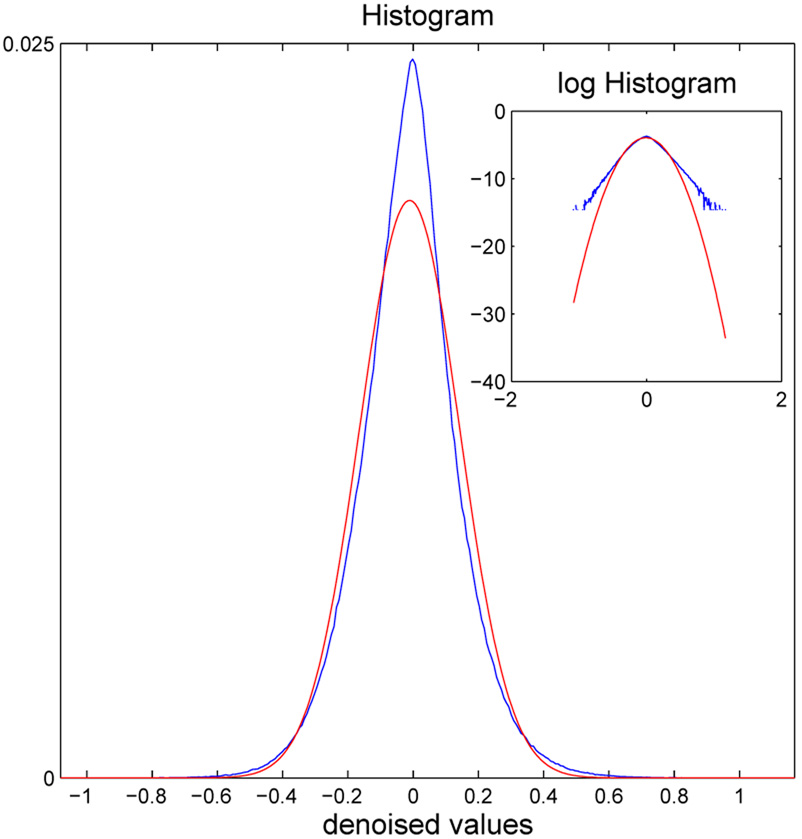
The last step of the procedure is to construct a histogram of the activation surface in the permuted data and use this sampled permutation distribution to assign a P-value to each statistic in the reduced search volume of the experimental data. The P-values are then thresholded using a standard algorithm to control the FDR at an arbitrary level, say α_FDR=0.01 As demonstrated in Fig. 3, an important advantage of using a permutation distribution for the final stage of significance testing is that the null distribution of the denoised activation statistics departs empirically from a Normal distribution, especially in the tails corresponding to the small P-values likely to be of greatest relevance to multiple hypothesis testing.

Figure 3.

Motivation for permutation testing of activation statistics after denoising by Bayesian shrinkage in the wavelet domain. The empirical histogram of denoised statistics (blue line) can be compared to the best-fitting Gaussian distribution (red line). It is clear, especially from the inset plots of these curves on a log scale, that the empirical distribution is more heavy-tailed than the Gaussian distribution, implying that hypothesis testing based on critical values in the tails of the Gaussian distribution would likely lead to uncontrolled Type I error.

Results

Type I error control

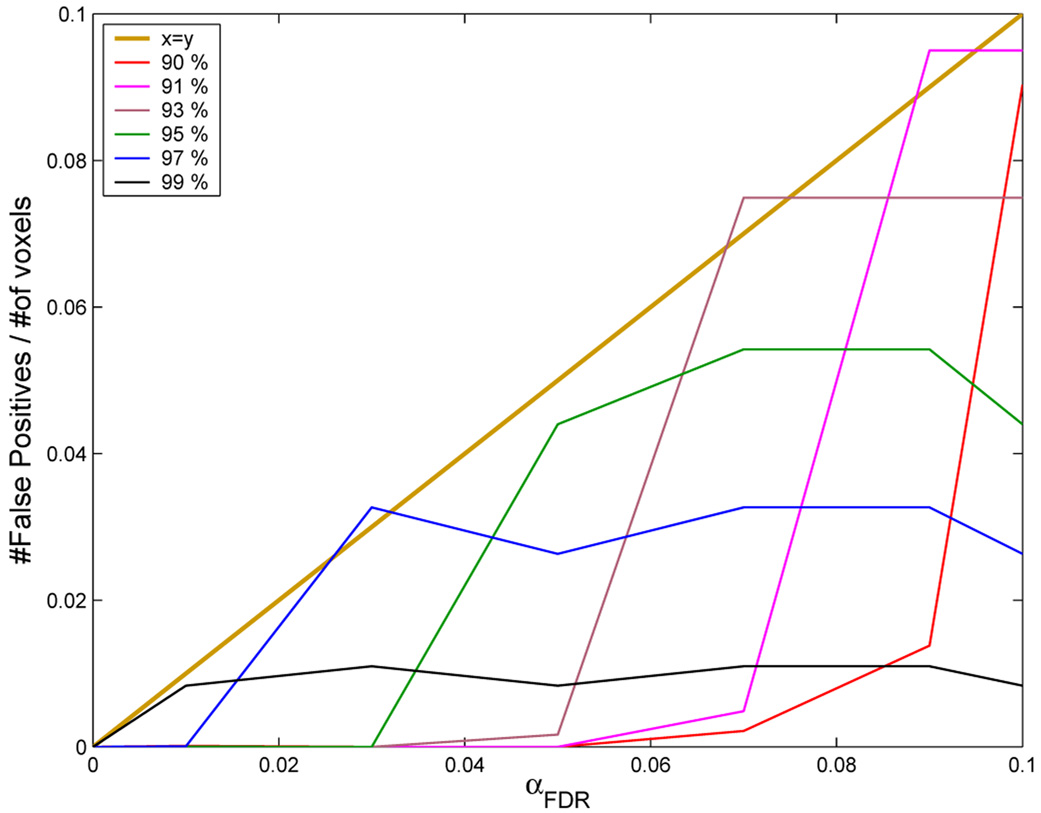
To assess Type I error control by this procedure, we applied the algorithm to analysis of a permuted statistic map, representing the spatial distribution of activation statistics under the null hypothesis. For a significance testing procedure to be valid, the number of positive tests under the null hypothesis should be less than or equal to the number of tests multiplied by the size of the test. As shown in Fig. 4, the proposed algorithm is valid by this criterion for several choices of τ_s and α_FDR.

Figure 4.

Demonstration of nominal Type 1 error control: y-axis, observed probability of a positive test; x-axis, probability of a positive test expected under the null hypothesis, α_FDR. A valid hypothesis testing algorithm must yield an observed number of positive tests that is less than or equal to the number of positive tests predicted under the null hypothesis, i.e., the observed number of positive tests must fall below the dark blue line (y = x) for any size of α_FDR The other lines indicate the number of positive tests observed for different values of the preliminary threshold τ_s and for different sizes of α_FDR at each threshold value. It is clear that, for all values ofτ_s and α_FDR , the hypothesis testing procedure is valid. The algorithm is least conservative, i.e., the observed number of positive tests most closely approximates the expected number of positive tests, when α_FDR ~ τ_s.

FIAC experimental data

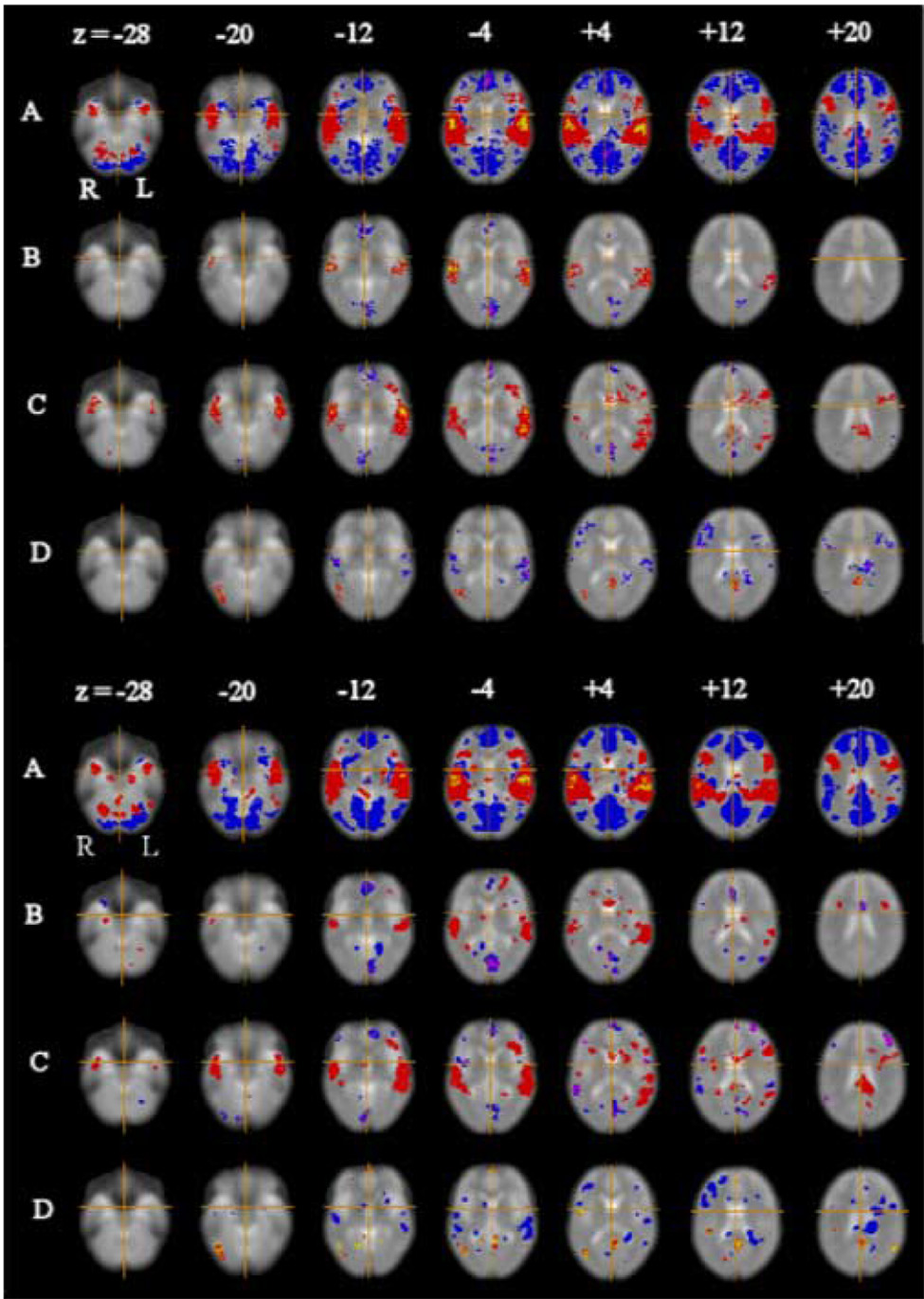
Using τ_s corresponding to the 99 percentile of the activation surface and α_FDR=0.01, we mapped voxels significantly activated by all four orthogonal contrasts estimated in analysis of the FIAC experimental dataset (Fig. 5). The results showed multiple areas of regional activation and deactivation that were very similar in their anatomical configuration to the results previously reported by analysis of the same dataset using a cluster-level permutation test in the spatial domain. Indeed, there is some evidence for incrementally greater sensitivity of the wavelet-based analysis in terms of more extensive representation of activation foci in bilateral superior temporal cortex.

Figure 5.

Activation maps for language processing experiment. Top panel: results previously reported by Suckling et al (2004), using a permutation test in the spatial domain. Bottom panel: results obtained by permutation testing of activation statistics in the spatial domain after Bayesian denoising in the wavelet domain. In both panels selected axial slices (at Talairach z-coordinates −28, −20, −12, −4, +4, +12, and +20 mm) are shown for (A) average activation difference between language processing and baseline conditions; (B) main effect of speaker novelty; (C) main effect of sentence novelty; and (D) interaction between sentence and speaker novelty. In both panels, the left-hand side of the image is the right-hand side of the brain and the crosshairs show the origin of the x and y coordinates in Talairach space. Red regions of A are where language processing conditions elicited greater response than baseline conditions and vice versa for blue regions. Red regions of B are where novel speaker blocks elicited greater response than familiar speaker blocks and vice versa for blue regions. Red regions of C are where novel sentence blocks elicited greater response than familiar sentence blocks and vice versa for blue regions. Red regions of D show where response to familiar sentence blocks was specifically increased when spoken by a novel speaker and response to novel sentence blocks was specifically decreased when spoken by a novel speaker and vice versa for blue regions. Type I error for the spatial permutation test (panel A) controlled the expected number of false positive tests at less than one per map; type I error for the permutation test after wavelet denoising (panel B) controlled the false discovery rate at α _FDR =0.01 for each map.

Discussion

In this note, we have confirmed that the spatial covariance of fMRI parameter maps is not white Gaussian and we have proposed using a wavelet-based resampling procedure to improve level-specific estimates of the 2D wavelet variance spectrum under the null hypothesis. We have combined this innovation with a previously described Bayesian bivariate shrinkage operator for denoising 2D wavelet coefficients. We have then used resampling-based threshold values for significance testing of voxel statistics in the spatial domain, after inversion of the denoised 2D wavelet coefficients. We have shown that overall this algorithm maintains acceptable Type I error control and can produce activation maps from an experimental dataset that appear to be somewhat more sensitive to experimentally-induced signals than comparable maps generated by a non-parametric hypothesis testing algorithm in the spatial domain.

Overall this work represents a convergence of previous efforts using wavelet transforms to resample fMRI time series under the null hypothesis (Bullmore et al 2001; Breakspear et al 2004; Patel et al 2006) with work using the 2D discrete or complex wavelet transform as a basis for multiple hypothesis testing of parametric maps derived from fMRI time series analysis (Ruttimann et al 1998; Shen et al 2002; Fadili & Bullmore 2004; Van de Ville et al 2004) or other functional neuroimaging data (Turkheimer et al 2004). Here we have used permutation of 1D discrete wavelet transform coefficients to resample the time series data but in principle the algorithm could be generalized to other, related approaches such as 4D spatiotemporal wavelet packet resampling (Patel et al 2006). Our approach to spatial hypothesis testing is similar to the method proposed by Van de Ville et al (2004) but differs by using estimates of sub-band specific variance for wavelet shrinkage of the spatial statistic maps, and critical values for hypothesis testing of denoised statistics, that are derived from wavelet resampling of the time series.

It will be interesting in future work to assess the differential sensitivity and specificity of these methodologically related approaches in analysis of simulated data. Nevertheless, such comparisons, especially on the basis of experimental data, are difficult to achieve with accuracy and robustness and are beyond the scope of this note. Here we restrict ourselves to the technical point that unrealistic and potentailly misleading assumptions about whiteness of spatial covariance have historically dominated the literature on wavelet analysis of 2D maps, yet can quite easily be circumvented by data resampling techniques.

To use this algorithm, only two parameters must be defined by the user: the percentile value for the preliminary threshold τ_s applied to the activation surface after wavelet denoising; and the false discovery rate α_FDR for the final test of a restricted subset of voxel statistics. The results obtained from an analysis of permuted statistic maps, where we expect there to be no truly activated voxels, indicate that any reasonable choice of these two parameters is associated with valid Type I error control. In other words, the number of positive tests is always less than or equal to the number of positive tests expected under the null hypothesis. Moreover, it seems that the sensitivity of the algorithm is likely to be greatest when τ_s ~ 1−α_FDR; so the user’s choice could be restricted to defining α_FDR < 0.05 and τ_s could be defined automatically based on this relation.