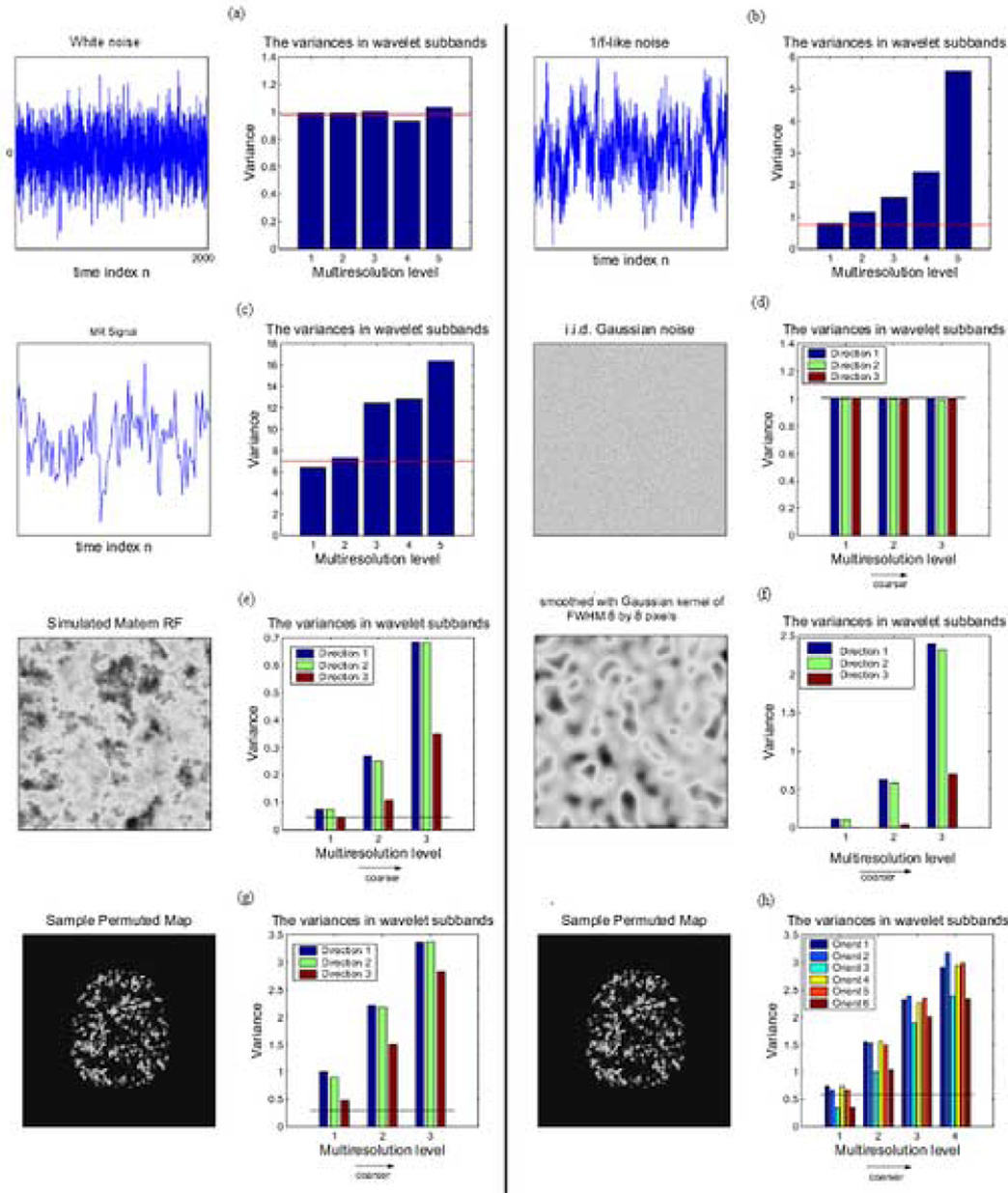
Figure 2.

Gaussian and non-Gaussian spatial (2D) and temporal (1D) signals and their corresponding wavelet variance spectra. a) 1D white noise has a flat wavelet variance spectrum where the variance at each scale is well approximated by an estimator based on the median absolute deviation (MAD) of the finest scale wavelet coefficients. b) Simulated 1D 1/f signal shows greater variance of the wavelet coefficients representing lower frequency trends in the time series, which is not well approximated by the MAD-based estimator. c) A functional MRI time series, acquired from a subject “at rest” (without experimental stimulation), has a wavelet variance spectrum similar to simulated 1D 1/f noise. d) A 2D spatial process with white Gaussian covariance has a flat 2D wavelet variance spectrum, i.e., the variances at all scales and orientations of the DWT are well approximated by the MAD-based estimator. e) A simulated Matern class spatial process and f) a smoothed Gaussian random field both have a wavelet variance spectrum with greater varainces of coefficients representing coarser scale spatial features. g) A permuted fMRI parameter map has greater variance of discrete wavelet transform coefficients, and h) complex wavelet transform coefficients, representing coarser scale spatial features, which is not well approximated by the MAD-based variance estimator (shown as a solid red line in all panels).