Abstract
A novel numerical method is developed that integrates boundary-conforming grids with a sharp interface, immersed boundary methodology. The method is intended for simulating internal flows containing complex, moving immersed boundaries such as those encountered in several cardiovascular applications. The background domain (e.g the empty aorta) is discretized efficiently with a curvilinear boundary-fitted mesh while the complex moving immersed boundary (say a prosthetic heart valve) is treated with the sharp-interface, hybrid Cartesian/immersed-boundary approach of Gilmanov and Sotiropoulos [1]. To facilitate the implementation of this novel modeling paradigm in complex flow simulations, an accurate and efficient numerical method is developed for solving the unsteady, incompressible Navier-Stokes equations in generalized curvilinear coordinates. The method employs a novel, fully-curvilinear staggered grid discretization approach, which does not require either the explicit evaluation of the Christoffel symbols or the discretization of all three momentum equations at cell interfaces as done in previous formulations. The equations are integrated in time using an efficient, second-order accurate fractional step methodology coupled with a Jacobian-free, Newton-Krylov solver for the momentum equations and a GMRES solver enhanced with multigrid as preconditioner for the Poisson equation. Several numerical experiments are carried out on fine computational meshes to demonstrate the accuracy and efficiency of the proposed method for standard benchmark problems as well as for unsteady, pulsatile flow through a curved, pipe bend. To demonstrate the ability of the method to simulate flows with complex, moving immersed boundaries we apply it to calculate pulsatile, physiological flow through a mechanical, bileaflet heart valve mounted in a model straight aorta with an anatomical-like triple sinus.
1 Introduction
There is growing recent interest in the development of non-boundary conforming numerical techniques for simulating flows in domains with arbitrarily complex, immersed boundaries. Depending on the approach adopted to satisfy the boundary conditions on solid surfaces, such techniques can be broadly classified as diffused or sharp interface methodologies. The former methods are known as immersed boundary formulations and tend to smear a solid boundary across few grid nodes due to the discrete delta function formulation they employ to introduce the effect of the boundary on the equations of motion [2]. The latter class of methods, on the other hand, treats solid boundaries as sharp interfaces utilizing either Cartesian, cut-cell formulations [3, 4] or hybrid Cartesian/Immersed Boundary (HCIB) approaches (see [5, 6, 1, 7] among others)—the reader is referred to [8, 9] for more detailed discussion of this class of methods. Regardless on whether a diffused or a sharp interface formulation is employed, however, all available non-boundary conforming methods solve the Navier-Stokes equations in a background coordinate-conforming mesh, such as a Cartesian (e.g. [1]) or a cylindrical (e.g. [6]) mesh. This is an inherent feature of such methods as their derivation is motivated by the need to avoid constructing a curvilinear, boundary conforming mesh, which for arbitrarily complex boundaries could be difficult if not impossible to construct.
There are, however, situations where hybrid methodologies combining aspects of curvilinear, body-fitted methodologies with those of non-boundary conforming approaches could be desirable and beneficial. Such cases are often encountered in cardiovascular flow problems where a complex, flexible immersed boundary—say the leaflets of a native or a prosthetic heart valve—is embedded within a blood vessel. The empty blood vessel geometry can be easily and efficiently discretized with a body-fitted curvilinear mesh, which can greatly facilitate the accurate resolution of the vorticity produced within the near wall boundary layers. The arbitrarily complex, deformable immersed boundary, on the other hand, can only be treated using a non-boundary conforming methodology. Therefore, the numerical simulation of such problems could greatly benefit from developing hybrid numerical techniques for simulating complex immersed boundaries moving within a background domain discretized with a generalized curvilinear mesh. A critical prerequisite, however, for the successful implementation of this novel modeling paradigm to complex flow simulations is the development of an accurate and efficient numerical method for solving the incompressible Navier-Stokes equations in generalized curvilinear coordinates and on fine computational meshes. The objective of this paper is to develop such a numerical method and demonstrate that this method can be used as the base flow solver for simulating unsteady flows with moving boundaries immersed in a curvilinear background mesh.
Our method is based on the recently developed HCIB formulation of Gilmanov and Sotiropoulos [1] who proposed a novel formulation for solving the incompressible Navier-Stokes equations on a hybrid, staggered/non-staggered grid layout. As discussed extensively in Gilmanov and Sotiropoulos [1] pure non-staggered grid formulations, even though easier to implement in conjunction with a HCIB approach, could lead to large errors in the satisfaction of the discrete continuity equation near rapidly accelerating immersed boundaries due to large induced pressure gradients. Staggered grid methodologies, on the other hand, can drive the discrete divergence to machine zero but are cumbersome to implement in the context of HCIB approaches. The hybrid, staggered/non-staggered grid methodology developed by Gilmanov and Sotiropoulos was shown to alleviate these difficulties and was successfully applied to simulate flows with arbitrarily complex, deformable bodies, including a swimming mackerel and a planktonic copepod. This method, however, is only applicable to Cartesian meshes. Thus, a major objective of our work is to extend the method of Gilmanov and Sotiropoulos to generalized curvilinear coordinates. In doing so we also address the broader problem of formulating staggered-grid methodologies in curvilinear coordinates [10, 11]. We show that the hybrid staggered/non-staggered grid approach of Gilmanov and Sotiropoulos can be used to satisfy the discrete continuity equation exactly in generalized, curvilinear coordinates without requiring the explicit evaluation of Christoffel symbols in the governing equations or the discretization of all three equations for the Cartesian velocity components at all surfaces of each control volume.
Another major objective of our work is to enhance the efficiency of the explicit iterative solver of Gilmanov and Sotiropoulos so that the method can be used to solve the unsteady, incompressible Navier-Stoke in generalized coordinates and on fine computational meshes. As our work is motivated by pulsatile flow problems in cardiovascular anatomies, the issue of computational efficiency becomes especially challenging. It is well known, for instance, that the performance of incompressible flow solvers deteriorates rapidly in pulsatile flow simulations where a new mass flux has to be propagated through the entire computational domain at each time step [12]. In this work we show that a fractional step formulation, coupled with a generalized, minimal residual (GMRES) solver with multigrid as preconditioner for the pressure equation can greatly enhance computational efficiency in pulsatile flow simulations.
Our paper is organized as follows. In section 2 we present the governing equations in generalized curvilinear coordinates. In section 3, we illustrate the difficulties encountered in staggered mesh formulations in curvilinear coordinates and review previous approaches for handling these difficulties. Subsequently we extend the hybrid staggered/non-staggered mesh formulation of Gilmanov and Sotiropoulos to curvilinear coordinates and show how this new formulation can alleviate shortcoming of previous approaches. In section 5 we discuss the fractional step approach used to solve the discrete equations, which is based on a multigrid preconditioned GMRES iteration scheme for solving the pressure equation. In section 7 we analyze the efficiency and spatial accuracy of the method by conducting numerical experiments for various benchmark problems, including the classical 2D driven cavity problem, impulsively started flow in a long straight duct, and pulsatile flow though a 90° pipe bend. For the latter case the computed results are compared with the experimental measurements of Rindt et al. [13]. In section 7.4 we demonstrate the applicability of the method to flows with moving immersed boundaries by applying it to simulate pulsatile flow through a bileaflet mechanical heart valve mounted in a model, straight aorta geometry with an anatomical-like triple sinus geometry. Finally, in the last section of the paper we summarize the major findings of our research and discuss future further extensions of the numerical approach.
2 The Navier-Stokes Equations in Curvilinear Coordinates
For the sake of completeness and to introduce some of the notation we adopt in this work, we begin our discussion by presenting the incompressible Navier-Stokes equations for a Newtonian fluid in Cartesian coordinates. Using Einstein’s tensor notation, where repeated indices imply summation unless otherwise indicated, the governing equations read as follows(q, r = 1, 2, 3):
| (1) |
where {xr} are the Cartesian coordinates, {ur}are the Cartesian velocity components, p is the static pressure divided by the density ρ, and Re is the Reynold number of the flow based on a characteristic length and velocity scales.
When body-fitted curvilinear grids are used to discretize the computational domain, a generalized, curvilinear coordinate mapping is typically employed to transform the equations from Cartesian to curvilinear (ξ1, ξ2, ξ3) coordinates—where ξm = ξm (x1,x2, x3). There are two approaches one can adopt to implement such a coordinate transformation: the partial transformation and the full transformation.
In the partial transformation approach only the independent variables {xm} are transformed to curvilinear coordinates while the dependent variables, the components of the velocity field, are retained in terms of their Cartesian components {um}. The partially transformed equations read as follows:
| (2) |
| (3) |
where C, G, and D are the convective, gradient, and viscous operators defined in curvilinear coordinates as follows:
| (4) |
| (5) |
| (6) |
In the above equations, J is the Jacobian of the geometric transfornation J = ∂ (ξ1, ξ2, ξ3) /∂ (x1, x2, x3), grm is the contravariant metric tensor , and Uq are the contravariant velocity components, which are related with the Cartesian velocity components as follows:
| (7) |
| (8) |
In the full transformation approach both the dependent and independent variables are transformed in generalized curvilinear coordinates. Selecting the surface volume fluxes Vq, Vq = Uq/J, as the dependent variables the fully transformed governing equations read as follows:
| (9) |
| (10) |
The fully transformed convective, C, and viscous, D, operators read as follows:
The covariant derivative operator that appears in the above equations is defined as:
where are the Christoffel symbols of the second kind defined as
3 Overview of staggered grid formulations in curvilinear coordinates
Staggered grid methods in Cartesian coordinates typically locate the pressure at the control volume centers (i, j, k) and the velocity components at the surface centers (see Fig. 1)–(i + 1/2, j, k), (i, j + 1/2, k), (i, j, k + 1/2) for the u, v, and w velocity components, respectively [14]. The continuity equation is then discretized by intergating it at control volumes that coincide with each computational cell whereas each momentum equation is discretized by intergating it over a control volume centered at the corresponding surface center. Integrating the transformed continuity equation (Eq. (2) or Eq. (9)) over a given control volume leads to the following discrete approximation of the continuity equation:
| (11) |
where Di,j,k denotes the discrete divergence operator, and the dots imply terms in the other two spatial directions, which are omitted for convenience. As seen in the above equation, the discretized continuity equation requires the volume fluxes at all surface centers, which, by definition, equals to the product of the normal velocity and the surface area. In Cartesian coordinates, the normal velocity coincides with the Cartesian velocity component defined at the surface centers (Fig. 1). Thus, the discretization of the continuity equation can be accomplished in a straightforward manner as the required Cartesian velocity components are available at the surface centers. In generalized curvilinear coordinates, however, the volume fluxes at surface centers may or may not be directly available depending on the choice of dependent variables. It is this critical difference between Cartesian and curvilinear coordinates that is at the center of the difficulties encountered in curvilinear staggered grid formulations.
Fig. 1.
Velocity and pressure storage arrangement for a staggered grid layout.
If the partially transformed form of the governing equations is employed (Eq. (2) and Eq. (3)) then the volume fluxes at the surface centers are not available and need to be reconstructed from the Cartesian velocity components, as follows:
The rigorous and most accurate approach to accomplish the reconstruction is to define at each surface center all three Cartesian velocity components and calculate them by integrating in time the three momentum equations–we shall refer to this approach as PT-1. This approach has been successfully applied in the past, see for example Maliska and Raithby [15], but it essentially triples the computational cost of the curvilinear formulation relative to the Cartesian formulation as in the latter only one momentum equation is solved at each surface center. This increased cost could be very expensive in 3D simulations and has prompted the development of approximate formulations, which de-fine only one Cartesian component at each surface center of the curvilinear staggered mesh (i.e., u1 component at all (i + 1/2, j,k) locations and u2, u3 for the other two surface centers, respectively) and reconstruct the other two by interpolation–this approach will be denoted as PT-2. More specifically, according to this approach the volume flux at the (i + 1/2, j, k) surface center would be reconstructed by obtaining u1 directly from the solution of the x1-momentum equation and interpolating u2 and u3 from surrounding surface centers, where they are calculated by the solution of the respective momentum equations. The cost of the PT-2 approach is comparable to that of the Cartesian, staggered mesh formulation but this treatment works well only for geometries for which the primary flow direction along which say the ξ1-curvilinear coordinate remains aligned with one of the Cartesian velocity components. Consider for example a 90° curved duct with its straight entrance section along the horizontal, x1-direction. The curvilinear coordinate ξ1 along the stream-wise direction through the duct is initially aligned with the x1-axis but at the end of curvature it is oriented along the perpendicular x2-axis. Therefore, solving the u1 momentum equation at the (i+1/2,j,k) nodes and interpolating the other two velocity components to construct the volume flux will lead to the result of having to interpolate the primary velocity component at the end of curvature (the u2 component in this case). As shown in [16] this treatment could result in odd-even decoupling of the pressure nodes and as such the resulting algorithm is not suitable for simulating arbitrarily complex flows.
The above difficulties with the partially transformed version of the equations can be alleviated by using the fully transformed momentum equations, Eq. (9) and Eq. (10). In this case it is straightforward to design an algorithm that emulates the Cartesian, staggered grid formulation by defining the volume fluxes, V1, V2, and V3 at the (i + 1/2, j, k), (i, j + 1/2, k), and (i, j, k + 1/2) surface centers, respectively. This approach (denoted as FT-1), however, requires the solution of the fully transformed form of the Navier-Stokes equations, which are very complex and cumbersome to discretize. Furthermore, these equations involve the Christoffel symbols of the second kind, see Eq. (10), which are expensive to compute and store and increase significantly the requirements for smoothness of the computational mesh as they involve second order derivatives of the metrics of the geometric transformation. FT-1 formulations have been proposed and applied to solve the incompressible Navier-Stokes equations, see for example [17, 18], but because of the aforementioned difficulties such methods have not been widely used in the literature.
Stagerred grid strategies that employ the fully-transformed equations, albeit indirectly, and can be considered as hybrid techniques between the PT-1 and FT-1 formulations have been proposed and successfully applied in [19, 20, 11]. Methods in this category, which will be denoted here as FT-2 formulations, exploit the relationship between the volume fluxes and the Cartesian velocity components (see Eq. (7) above) to avoid dealing with the fully-transformed form of the Navier-Stokes equations directly. Namely, the transport equations for the volume fluxes are derived from the partially-transformed form of the Navier-Stokes equations as follows:
| (12) |
Using the definition of the pressure gradient operator given by Eq. (6), the above equation reads as follows:
| (13) |
Eq. (13) is essentially identical to the fully-transformed equation (9) and equation (10) but does not explicitly involve the Christoffel symbols, which of course will appear if the above equation is further manipulated. In a similar fashion as FT-1 formulations, FT-2 type methods discretize at each surface center the transport equation for the respective volume flux in the form given by Eq. (13). At the (i + 1/2, j, k) nodes, for instance, the V1 equation is semi-discretized as follows:
| (14) |
where
| (15) |
is the pressure gradient operator for curvilinear cooordinates and δξr is the central differencing operator at the surface center. The advantage of using the above discretization approach over the FT-1 formulation is that the explicit evaluation of the Christoffel symbols is avoided. This is accomplished, however, at the expense of having to discretize at each surface center the convective and viscous operators for all three Cartesian momentum equations. In other words, the computational cost for discretizing the governing equations with this approach is comparable to that of the PT-1 formulation [10].
In the following section we present a new approach, which reduces significantly the computational work required to discretize the governing equations.
4 Hybrid staggered/non-staggered approach in curvilinear coordinates
The curvilinear formulation we propose in this work is based on the hybrid staggered/non-staggered approach developed by Gilmanov and Sotiropoulos [1]. They were motivated by the need to develop a method for solving the Navier-Stokes equations in Cartesian meshes that facilitates the implementation of boundary conditions in flows with complex, moving, immersed boundaries while satisfies the discrete continuity equation exactly. In this section we show that the method of Gilmanov and Sotiropoulos is a natural choice for developing an efficient curvilinear formulation that has all the advantages of a pure staggered grid formulation (i.e. satisfies the discrete continuity exactly) and eliminates the need for discretizing the Christoffel symbols without the excessive additional computational cost of previous formulations.
We define and store the volume fluxes Vq at the respective surface centers (as in the FT-1 and FT-2 formulations) and the pressure at the volume centers. The volume fluxes are obtained by discretizing and solving their respective transport equations, which, for reasons that will soon become apparent, are formulated as follows:
| (16) |
where ℜq (q = 1, 2, 3) denote the contravariant fluxes of the convective and viscous terms:
| (17) |
The key difference between the proposed method and the FT-2 approach is that the ℜq terms at their respective surface centers are not obtained by discretizing the C and D terms at the surface centers (as required in approach FT-2 as shown in Eq. (14)) but are reconstructed by interpolation from the volume centers. This is accomplished by first re-constructing the Cartesian velocity components at the volume centers–(i, j, k) nodes–by interpolating the contravariant velocity components and using Eq. (8). With the Cartesian velocity components available at the volume centers the convective and viscous terms (C (um) and D(um) for m = 1, 2, 3) can be readily discretized using the discretization method of choice (see below for details) in the same manner as in a non-staggered mesh. Subsequently, the discrete approximations of the terms can be calculated using Eq. (17). This step is followed by interpolation to re-construct and the semi-discrete (in space) approximation of Eq. (16) reads as follows:
| (18) |
where is the same discrete curvilinear pressure gradient operator defined as in Eq. (15). Obviously the proposed method is substantially more efficient that the FT-2 approach as it does not require the discretization of the convective and viscous terms for all three momentum equations at each surface center–a step, which as discussed earlier essentially triples the amount of computational work compared to a non-staggered grid method. Instead the cost for discretizing these terms in the present method is similar to that of a non-staggered mesh as their discretization takes place only once per time step at each (i, j, k) node. Of course relative to a non-staggered formulation, the present method does incur an additional computational overhead due to the intermediate re-construction steps needed to obtain the Cartesian velocity components at the volume centers and then project back the discrete convective and viscous terms at the surface centers. As we will subsequently discuss, however, the various re-construction steps involve local, one-dimensional interpolations in the transformed space and as such the computational cost associated with them is minimal. The details of the implementation of the various steps of the proposed method are as follows.
Let us assume that the volume fluxes at their respective surface centers are known at a given time step– Reconstruction of the Cartesian velocity components at the volume centers–(ur)i,j,k (r = 1, 2, 3) –is accomplished using the one-dimensional QUICK [21] interpolation formula, which was also employed for the Cartesian mesh analogue of the method by Gilmanov and Sotiropoulos [1]. For example, the V 1 volume flux is calculated by interpolating along the ξ1 direction as follows: assuming the grid volumes centers along i direction is numbered from 1, 2, … imax,
| (19) |
Similarly the V2 and V3 volume fluxes are determined by interpolating along their respective grid lines (j and k lines, respectively). With all three volume fluxes known at the volume centers the three contravariant and Cartesian velocity components can be readily computed using Eq. (8).
At the end of this step the Cartesian velocity components are available at the volume centers and the partially transformed convective, C(ur), and viscous, D(ur), terms for the three momentum equations (Eq. (4) and Eq. (5)) can be readily discretized in a manner similar to a non-staggered grid formulation. In this work we employ the QUICK scheme to discretize the convective terms and standard, three-point central differencing to discretize the viscous terms. Subsequently the discrete approximations of the contravariant fluxes of the convective and viscous terms can be calculated at the volume centers (q = 1,2,3) using Eq. (17).
The final step for completing the discretization of the transport equations for the volume fluxes according to Eq. (18) is to re-construct the ℜq terms at their respective surface centers. Here, similarly as in [1], we use the following QUICK scheme (see [1] for a discussion on the rationale for biasing the direction of the interpolation scheme):
| (20) |
Similar interpolation formulas are used to obtain along the j and k grid lines, respectively.
5 Time Integration Scheme
We employ a fractional step method similar to that proposed in [22] to integrate the governing equations in time. First, intermediate volume fluxes Vq(*) that do not satisfy continuity are calculated by solving implicitly (see below for details) the following momentum equations at the surface centers (we shall denote this step as the momentum step):
| (21) |
where Vq(n) represents the solution at time step n, and Gq is the curvilinear gradient operator expressed as in Eq. (15). In the above equations, the time derivative is discretized with a second-order backward Euler scheme and the right hand side is calculated using the previously described hybrid staggered/non-staggered approach.
The above step is followed by a pressure correction step to satisfy the continuity equation:
| (22) |
| (23) |
where Di,j,k(·) is the discrete divergence operator defined in Eq. (11) and ϕ is the pressure correction, whose value is obtained by solving the following Poisson equation:
| (24) |
The pressure at the new time step n + 1 can be recovered as
| (25) |
Both the momentum and pressure-correction steps result in large sparse systems. The numerical algorithms we employ for solving the two steps are described below.
5.1 Implicit solution of the momentum step
Our preliminary attempts to handle ℜ in Eq. (21) explicitly were not successful, especially in fine-mesh, pulsatile flow simulations. The explicit evaluation of ℜ imposed severe restrictions on the physical time step Δt and was further found to undermine the stability of the entire fractional step approach. Implicit treatment of ℜ, however, is not straightforward and requires careful consideration. A direct approach would require the inversion of a very large nonlinear sparse matrix and the resulting algorithm would be far too expensive to be practical. As such, alternative iterative solvers, such as Newton-Krylov methods or approximate factorization methods, provide the only feasible solution. Approximate factorization methods, say such as that developed by Beam and Warming [23], require the evaluation of the Jacobian of the right hand side of Eq. (21). It is easy to see, however, that in the present case the calculation of the Jacobian could be very costly as it would require the evaluation of the Christoffel symbols, which is exactly what we tried to avoid in the first place by developing the hybrid staggered/non-staggered grid approach. To circumvent this difficulty we employ a matrix-free, Newton-Krylov method. In what follows, we will briefly review the basic concepts of such methods in the context of the present problem–see [24] for a recent comprehensive review of the current state of development and application of matrix-free Newton-Krylov methods.
The semi-discretized momentum equation Eq. (21) can be reorganized as follows:
| (26) |
Advancing Eq. (21) implicitly in time is essentially equivalent to seeking the solution of the equation F(Vq*) = 0, which can be efficiently accomplished through the following Newton-like iteration scheme:
| (27) |
where k is the iteration counter, is the Jacobian matrix. The correction at the kth step of Newton iteration can be obtained by solving the following linear system:
| (28) |
using a Krylov subspace method, such as GMRES [25]. Solving the above linear system with GMRES, however, does not require the explicit evaluation of the Jacobian matrix 𝕵 but only the matrix vector product 𝕵δV. Following Brown and Saad [26], this product can be approximated as follows:
where h is a small perturbation.
In this work we employ the matrix-free Newton-Krylov solver implemented in PETSc [27] to efficiently solve Eq. (21). Typically about 5–7 Newton iterations are required to reduce the residual of F(Vq*) by 5 orders or more.
5.2 Solution of the pressure-correction equation
It is well-known that the overall efficiency of any fractional step method for solving the incompressible Navier-Stokes equations largely depends on the approach adopted to solve the pressure correction equation, Eq. (24). If one seeks to solve the Poisson equation in simple coordinates–for example, rectangular domain with Cartesian grids or circular domain with cylindrical grid systems–the solution can be efficiently obtained through direct solvers [28, 29]. These direct methods, however, are not useful for our work as we are interested in complicated flow domains using generalized curvilinear grids. Iterative methods are the only feasible alternative to the discrete Poisson equation arising in such curvilinear grid systems. The most efficient iterative solvers available today include Krylov subspace methods, such as GMRES and BICGSTAB [30], and multigrid methods. In our work, we employ a Flexible GMRES (FGMRES) solver [31] to solve the Poisson equation. Typically a GMRES solver is used together with a pre-conditioner, such as Jacobi, SOR, incomplete LU (ILU) decomposition [32], etc., in order to improve its robustness and efficiency. As we will subsequently show through numerical experiments in section 7.2, the convergence performance of the GMRES solver with simple pre-conditioner (such as Jacobi or ILU) deteriorates dramatically with increasing mesh size for the problems we are interested in. Such grid-size-dependent convergence performance can be effectively addressed by using a multigrid method as preconditioner for the GMRES solver [33]. As illustrated in [33], a multigrid-preconditioned GMRES solver is very robust and its overall performance is far superior than that of the multigrid method alone. In our work, we employ a cell-centered multigrid method as the preconditioner for the FGMRES solver. Upon constructing the multigrid preconditioner, we need to choose the grid coarsening strategy, smoother for fine grid levels and coarsest grid level solver, as well as the restriction and interpolation operators. For grid coarsening we implemented and tested both full coarsening and semi-coarsening strategies. The multigrid preconditioner uses ILU decomposition as smoother for the fine grid levels and the coarsest grid level equation is efficiently solved through a Krylov subspace solver (GMRES or BICGSTAB). We use the standard trilin-ear interpolation operator for the restriction and interpolation between different levels [34] and these operators are provided as subroutines. The coefficient matrices at each grid level are obtained by discretizing the left hand side of Eq. 24 at the corresponding grid level and their values are stored in the memory for improved performance. In section 7.2, we evaluate the convergence performance of the Poisson equation solver and show that multigrid-preconditioned GMRES can solve the discrete pressure Poisson equation very efficiently on fines meshes.
6 Sharp Interface Immersed boundary method
As stated in the introduction of this paper, our objective is to combine sharp-interface, immersed boundary methodologies with a background curvilinear mesh in order to effectively handle complex, internal flows with flexible immersed boundaries.The curvilinear Navier-Stokes solver described above is thus integrated with the HCIB approach of Gilmanov and Sotiropoulos [1]. The details of the method can be found in [1]. Here it suffices to state that the method employs an unstructured, triangular mesh to discretize and track the position of a complex, moving immersed boundary, which is handled as a sharp interface. The presence of the boundary on surrounding fluid nodes is accounted for by reconstructing boundary conditions for the velocity field at grid nodes in the immediate vicinity of the boundary (the so-called immersed boundary nodes) by interpolating along the local normal to the boundary. Since in the current scheme the discretization of the right hand side terms are accomplished at volume centers (where the reconstructed Cartesian velocity components are located), the reconstruction methodology of Gilmanov and Sotiropoulos [1] can be readily implemented without any modifications and will not be discussed further. The reconstruction method has been shown to be second-order accurate on Cartesian grids with moving immersed boundaries[1]. The capability of the combined curvilinear grid /immersed boundary method will be illustrated in section 7.4, where we apply it to simulate flow through a bileaflet mechanical heart valve inserted in a modeled aorta with an anatomic-like, triple sinus structure.
7 Numerical Results
In this section we report a series of numerical experiments aimed at demonstrating the accuracy and efficiency of the numerical method. We also present a series of calculations for pulsatile flow in a 90° pipe flow aimed at validating the base flow solver. The ability of the method to simulate complex flows with moving boundaries immersed in a curvilinear background mesh is also demonstrated by reporting results from the calculation of pulsatile flow in a mechanical bileaflet heart valve.
7.1 2D Driven Cavity
As we have already discussed, the present numerical method is the extension of the Cartesian method developed by Gilmanov and Sotiropoulos [1] to generalized curvilinear coordinates at least insofar as the hybrid staggered / non-staggered grid discretization and immersed boundary reconstruction technique are concerned. Gilmanov and Sotiropoulos [1] carried out grid-refinement studies to demonstrate that their method is second-order accurate for flows with moving immersed boundaries. Since when the present method is applied to a Cartesian mesh it reduces to the discretization approach of [1], second-order convergence rate should also be anticipated and numerical tests have indeed verified this conclusion. In this section we focus our attention on the spatial accuracy of the base flow solver when applied to generalized curvilinear coordinate systems. Carrying out a rigorous grid refinement study in a curvilinear mesh, however, is not straightforward due to the fact that the grid spacing varies throughout the computational domain. For that we adopt an indirect approach to demonstrate the accuracy of the proposed curvilinear staggered/non-staggered grid discretization approach. We carry out numerical simulations on both Cartesian uniform and stretched curvilinear grids and compare the numerical solutions to show that the latter yield results that are essentially indistinguishable from the former. Note that a similar general approach was also adopted by Wesseling et al. [11] to demonstrate the accuracy of their curvilinear staggered grid method.
We select the standard 2D driven cavity (DC) problem [35], which is a widely used benchmark test case for incompressible flow solvers. We consider three computational meshes all with 332 grid nodes: DC_g1 is the base uniform Cartesian mesh while DC_g2 and DC_g3 are both distorted curvilinear grids (see Fig. 2). The two curvilinear meshes are purposely distorted in order to set up challenging computational tests for the various aspects of the staggered / non-staggered grid discretization (reconstruction of Cartesian velocity components at cell centers, interpolation of the convective and viscous terms at surface centers, etc.). The curvilinear mesh DC_g2 (shown in Fig. 2 (a)) is constructed by selecting the four edges of the driven cavity as the boundaries of the curvilinear. On each edge, the grid nodes are distributed with a hyperbolic tangent distribution function with the grid spacing at one end specified as 0.01 and the other one 0.04. The curvilinear grid DC_g3 is constructed by dividing the moving lid of the cavity into two segments by introducing an arbitrary albeit strategically selected point (point D in Fig. 2 (b)). The right boundary of the so resulting computational domain consists of the horizontal portion of the lid to the right of point D and the vertical right edge of the cavity. The corner singularity in this boundary results in a severely distorted and discontinuous mesh in a critical region of the flowfield, i.e. the region where the vorticity generated by the moving lid is ejected into the flowfield to set up the overall recirculating flow pattern. Naturally such an irrational mesh topology would never be used for simulating the driven cavity flow but it is selected herein in order to test the accuracy of the numerical method under severe mesh continuity and smoothness conditions. Note, however, that highly distorted grid cells such as those generated at the upper right corner of the cavity in DC_g3 mesh are quite frequently encountered in complex geometries discretized with body-fitted curvilinear grids.
Fig. 2.
Two deliberately distorted curvilinear grids for the driven cavity flow. The four letters mark the corners of the transformed domain in curvilinear space.
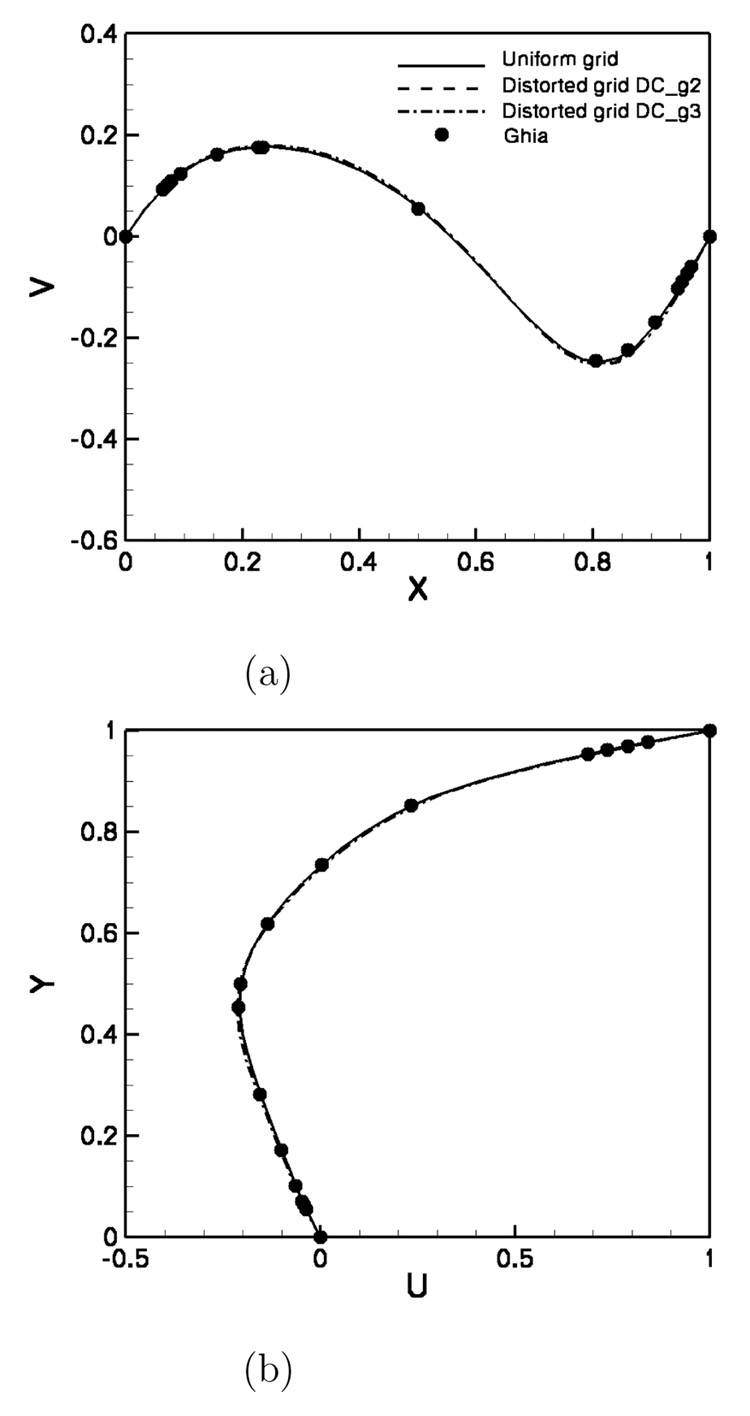
We carried out numerical simulations for both Re = 100 and 1000 on all three grids. Steady state solutions are obtained on all calculations. The computed results are compared with each other in Fig. 3 – Fig. 6. As seen in Fig. 3 and Fig. 5, which illustrate the velocity profile along the vertical and horizontal center lines, the velocity field obtained on these three different grid systems are almost identical to each other. What is more encouraging, however, is that the vorticity fields on all three grids are very close to each other, as shown in Fig. 4 and Fig. 6.
Fig. 3.
Velocity profile comparisons (Re = 100): (a) profile of vertical velocity component, v, along horizontal center line; (b) profile of horizontal velocity component, u, along vertical center line. The points show benchmark result from [35]. DC_g1 is the uniform Cartesian grid. DC_g2 and DC_g3 are the distorted curvilinear grids shown in Fig. 2 (a) and (b), respectively.
Fig. 6.
Comparisons of vorticity contours (Re = 1000). Solid lines: DC_g1; Dashed lines: DC_g2; Dotted lines: DC_g3. DC_g1 is the uniform Cartesian grid. DC_g2 and DC_g3 are the distorted curvilinear grids shown in Fig. 2 (a) and (b), respectively.
Fig. 5.
Velocity profile comparisons (Re = 1000): (a) profile of vertical velocity component, v, along horizontal center line; (b) profile of horizontal velocity component, u, along vertical center line. DC_g1 is the uniform Cartesian grid. DC_g2 and DC_g3 are the distorted curvilinear grids shown in Fig. 2 (a) and (b), respectively.
Fig. 4.
Comparisons of vorticity contours (Re = 100). Solid lines: DC_g1; Dashed lines: DC_g2; Dotted lines: DC_g3. DC_g1 is the uniform Cartesian grid. DC_g2 and DC_g3 are the distorted curvilinear grids shown in Fig. 2 (a) and (b), respectively.
These comparisons clearly demonstrates the ability of our curvilinear staggered / non-staggered grid approach to yield accurate solutions on very distorted meshes that are unavoidable in practical simulations of real-life engineering flows. It is also important to emphasize here that these results underscore the success of our interpolation procedure for reconstructing both the Cartesian velocity components at cell centers and the convective and viscous terms at surface centers. As we discussed in section 4 the interpolation for both cases is carried out in the transformed space so that the interpolation coefficients remain constant and do not depend locally on the grid spacing (see Eq. (19) and Eq. (20)). The results shown in Fig. 3 – Fig. 6 attest to the accuracy of our approach, which should be attributed to the fact that we interpolate contarvariant fluxes Vq and/or ℜq. Fluxes have by definition the information about the local area of the surface centers embedded in them, thus, accounting for the variations in mesh spacing automatically even though the interpolation is carried out in the uniform transformed curvilinear space.
7.2 Impulsively started pipe flow
This case is specifically designed to measure the efficiency of the Poisson equation solver. We consider laminar, impulsively started flow in a straight square duct of length l and height d = 1 (Fig. 7). The flow is initially (t = 0) stagnant everywhere. At t = 0+, the flow is impulsively accelerated by imposing a uniform incoming flow of constant velocity U = 1 at the inlet. Following the impulsive input at the inlet, the flow within the duct will develop toward a fully-developed steady state assuming that l is sufficiently long. When this flow is simulated in a time-accurate manner, the very first time step of the simulation poses a challenging test for the efficiency of any incompressible flow solver. During this first time step the flow will undergo the most dramatic change as the flow rate at each stream-wise section downstream of the inlet should adjust instantaneously from zero to the inlet value. This very first time step can also be thought as representative of the problem an incompressible flow solver will have to solve during each time step of a pulsatile flow simulation where the inlet flow rate is continuously changing with time. Finally, since the convergence rate of iterative solvers is known to deteriorate with aspect ratio, the severity of this problem from the standpoint of the Poisson solver can be further exacerbated by appropriately varying the aspect ratio l/d of the duct. For these reasons we select the impulsively accelerated straight duct flow from the initial time t = 0+ to t = Δt as the test case to gauge the performance of the various versions of GMRES-based solvers for the Poisson equation and demonstrate the superior performance of the multigrid-preconditioned GMRES approach. Calculations are carried out using the numerical procedure described in section 5 for Re = 100 (based on U and d), Δt = 0.01, various l/d values, and successively finer meshes. All tests in this sections have been carried out by running the code in parallel on 4 CPUs and using system clock time to measure the time required by the flow solver for each case. The so measured CPU time is scaled by the number of grid nodes to provide an objective measure of the computational work associated with each algorithm.
Fig. 7.
Sketch of the straight duct geometry with unit square cross-section.
The first set of numerical experiments is designed to gauge the effect of grid refinement on the efficiency of the flow solver while the mesh aspect ratio is kept constant and equal to 1. We set l = d = 1 and consider three, successively finer uniform grids: 333, 653 and 1293. The performance of the iterative solver is measured through the convergence rate, which is defined as:
where r(k) is the residual for the discrete divergence of the velocity field at the kth step iteration and ‖·‖2 denotes the L2-norm. In Fig. 8 we compare the performance of the FGMRES solver preconditioned with ILU pre-conditioner (Fig. 8 (a)) and with (Fig. 8 (b)) the multigrid preconditioner by plotting the convergence rate versus CPU time per grid node. As clearly evident from Fig. 8 (a), the convergence rate of the FGMRES solver with ILU pre-conditioner deteriorates rapidly as the grid is refined even though the mesh aspect ratio is one for all three grids. The implementation of the multigrid method as preconditioner to FGMRES, on the other hand, has a profound effiect on the efficiency of the solver. As seen in Fig. 8 (b), the multigrid-FGMRES algorithm yields a convergence rate that is nearly insensitive to mesh refinement especially when compared to the performance of the ILU preconditioned FGMRES. In fact on all three grid levels, the multigrid-FGMRES algorithm reduces the L2-norm of the error by at least 10 orders within 9 iterations.
Fig. 8.
Convergence performance of the FGMRES Poisson equation solver with different preconditioner for the impulsively started straight duct case (l = d = 1) during the first time step of the simulation. (a) ILU preconditioner; (b) multigrid preconditioner (each circle corresponding to one iteration of the FGMRES solver). γ is the L2-norm of the discrete divergence of the velocity field scaled with its value at the start of the iterative process. Straight line: 333 grid; Dash line: 653 grid; Dash-dot line: 1293 grid.
A second set of numerical experiments is carried out to investigate the effect of grid aspect ratio on the convergence of the pressure solver. It is well known that large grid aspect ratios can deteriorate the performance of the multigrid solver but this problem can be effectively addressed using an appropriate grid coarsening strategy [34]. To demonstrate the effect of the coarsening strategy on the performance of our method, we consider two flow domains with l = 10 and 100 both discretized with the same number of grid nodes (1013)-the grid spacing in each spatial direction is uniform. By construction the resulting meshes are uniform and have constant aspect ratios equal to 10 and 100, respectively. Fig. 9 compares the performance of the multigrid-FGMRES algorithm in conjunction with full-coarsening and semi-coarsening (grid is coarsened only in the transverse plane) for the two cases. Both coarsening strategies work well for the l = 10 case but the superior performance of the semi-coarsened multigrid preconditioner is evident for the l = 100 case. The semi-coarsened preconditioner appears to be nearly insensitive to grid aspect ratio while the performance of its full-coarsening counter-part deteriorates dramatically for the large aspect ratio case. In fact the convergence rate of the semi-coarsening algorithm is nearly one order of magnitude faster than that of the full-coarsening.
Fig. 9.
Effect of the coarsening strategy used in the multigrid preconditioner of the FGMRES Poisson equation solver for the impulsively started straight duct case during the first time step of the simulation. Two different duct aspect ratios are considered: (a) l/d = 10; (b) l/d = 100. For both cases a uniform mesh with 1293 grid nodes is used. γ is the L2-norm of the discrete divergence of the velocity field scaled with its value at the start of the iterative process. Solid line: Semi-coarsening; Dash line: Full-coarsening.
The superior performance of the semi-coarsening multigrid algorithm should be attributed to the fact that for the geometry under consideration coarsening the mesh only in the transverse plane results in coarser grids with successively smaller aspect ratios whereas full-coarsening preserves the fine-mesh aspect ratio on all mesh levels. Therefore, the FGMRES solver preconditioned with semi-coarsened multigrid should be expected to work well for geometries that have one dominant long spatial dimension. As such, the results presented in this section point to the conclusion that the semi-coarsening approach should be very efficient for the cardiovascular applications that have motivated the present work. This conclusion will be further reinforced in the results shown in the two subsequent sections.
7.3 Pulsatile flow in a 90° pipe bend
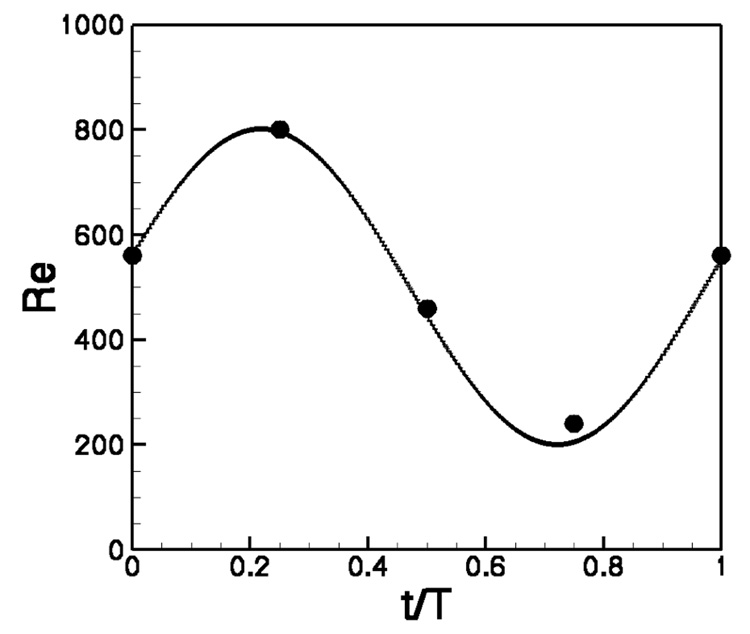
This test case is selected to demonstrate the accuracy and efficiency of our method in a complex, 3D pulsatile flow. We simulate numerically the curved pipe geometry studied experimentally by [13], which is shown in Fig. 10. The bend has a diameter of 8mm and radius of curvature equal to 24mm. A gear pump providing a steady flow of Re = 500 in conjunction with a piston pump generating a sinusoidal flow waveform with Reynolds number ranging from −300 to 300 were used in the experiment to generate the pulsatile flow wave-form shown in Fig. 11. The resulting Womersley number of the experimental flow is 7.8. The characteristic length and velocity scales used to calculate the non-dimensional numbers and non-dimensionalize the problem are the pipe diameter and median bulk velocity, respectively. The characteristic time scale is based on the characteristic length and velocity scales. The so resulting non-dimensional period of the incoming flow oscillation is T = 12.3.
Fig. 10.
Geometry and typical computational grid for the 90° pipe bend case. The diameter of the bend, d, equals to 8 mm. R denotes the radius from the center of bend curvature.
Fig. 11.
Incoming flow waveform. Solid line: Analytical flow waveform prescribed at the inlet of the flow domain obtained by assuming that the inlet flow follows the Womersley solution; Points: the measurements of [13]
The flow wave-form at the inlet is specified from the Womersley solution of a fully developed pulsatile flow within a circular pipe [36]:
| (29) |
where J0 denotes the Bessel function of the first kind and order zero, r is the radial distance from the center of the pipe, R is the radius of the pipe, ω represents the angular frequency of the flow oscillation, which is 13.31rad/s, and ν is the fluid viscosity. In order to generate the sinusoidal flow waveform that varies in accordance with the experiments from Re = 200 to Re = 800, the constant K is selected to be 0.375. We use Matlab to solve the above equation and the resulting solutions are stored and fed into the flow solver to specify the time-varying inlet flow. The so computed inflow waveform is in good overall agreement with the experimental inflow condition as shown in Fig. 11.
A curvilinear mesh is used to discretize the pipe cross-section (see Fig. 10) and calculations are carried out for three successively finer meshes: 41 × 41 × 81, 81 × 81 × 81 and 81 × 81 × 161 in the two transverse and stream-wise directions, respectively. Each pulsatile flow cycle is divided into 1000 time steps, with a corresponding non-dimensional time step ΔT = 0.0123. The typical convergence history of Poisson equation solver for this pulsatile flow computation is illustrated in Fig. 12, which shows the convergence history for the finest grid. As seen, the FGMRES solver preconditioned with semi-coarsened multigrid performs very well for this more complex flow case.
Fig. 12.
Pulsatile flow in a 90 deg pipe bend. Typical convergence histories of the discrete divergence of the velocity field for several time-steps during a pulsatile flow cycle on the 81 × 81 × 161 mesh.
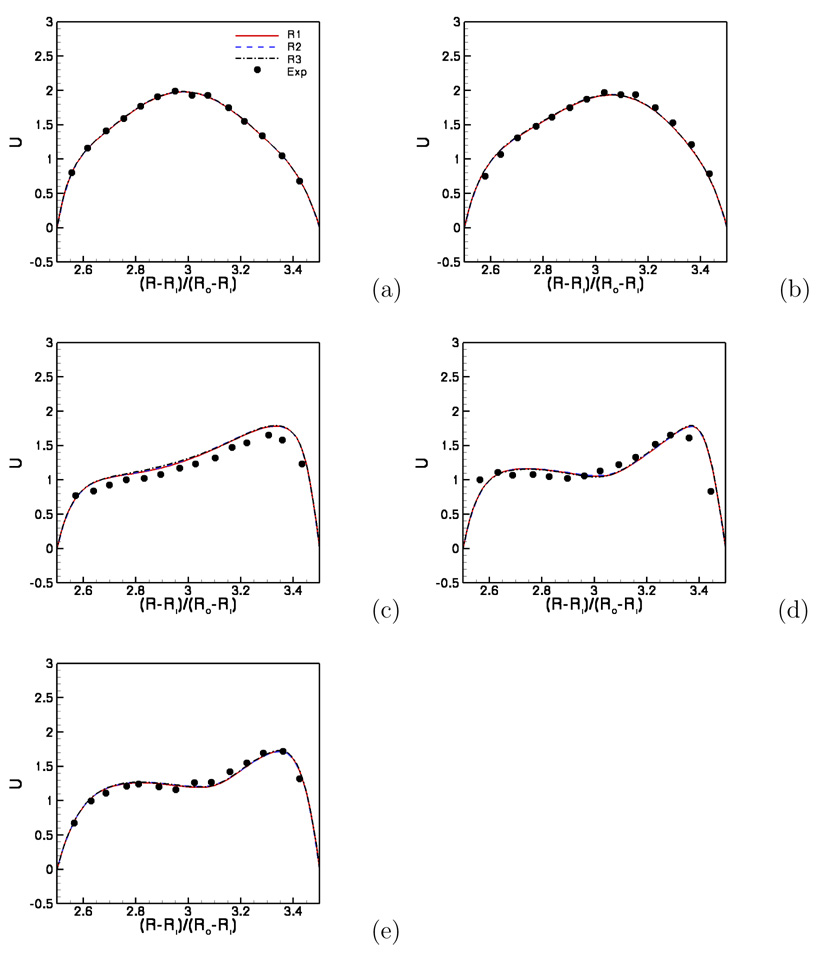
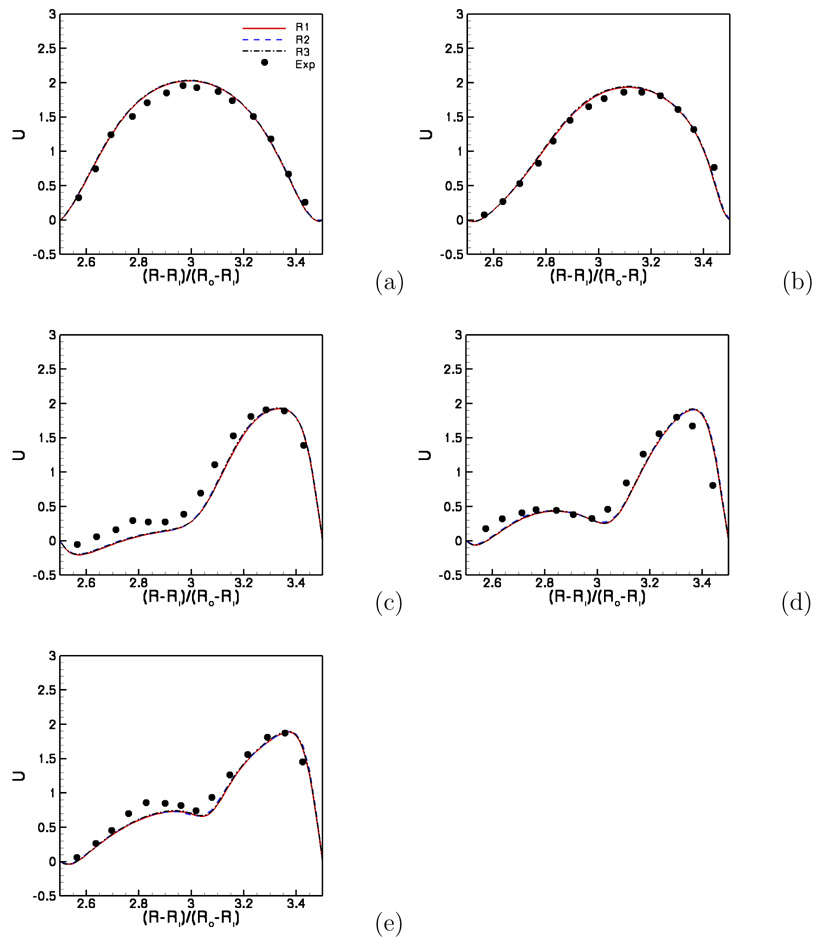
To validate our numerical simulation, we compare stream-wise velocity profiles from our simulations against the experiments in [13] at five different locations, which are θ = 0, 22.5°, 45°, 67.5° and 90° respectively. The stream-wise velocity profiles at four different time instants (0, 0.25T, 0.5T and 0.75T) are compared with the experimental measurements in Fig. 13 to Fig. 16. As seen in these figures even the coarsest mesh is adequate for obtaining grid independent solutions for this case. Furthermore, the calculated velocity profiles are in good agreement with measurements, with the largest overall discrepancies appearing at 0.75T time instant. Given the fact that all three meshes yield solutions that are identical to each other, this discrepancy could be largely attributed to the our inlet boundary conditions. As shown in Fig. 11, the wave-form prescribed at the inlet exhibits the largest deviation from the experimental wave form near t = 0.75T, i.e. the time instant when the largest discrepancies between the calculated and measured velocity fields are observed throughout the bend. This discrepancy not withstanding, however, the results presented in this section establish both the efficiency and accuracy of our method in complex, 3D pulsatile flow simulations.
Fig. 13.
Pulsatile flow in a 90 deg pipe bend. Measured (points) and computed stream-wise velocity profiles at t = 0. Solid line: 81 × 81 × 81 grid; Dash line: 41 × 41 × 81 grid; Dash-dot line: 81 × 81 × 161 grid. The five locations corresponding to (a) to (e) are θ = 0, 22.5°, 45°, 67.5°, and 90° respectively. Ri and Ro represent the inner and outer bend radius from the center of bend curvature.
Fig. 16.
Pulsatile flow in a 90 deg pipe bend. Measured (points) and computed stream-wise velocity profiles at t = 0.75T. Solid line: 81 × 81 × 81 grid; Dash line: 41 × 41 × 81 grid; Dash-dot line: 81 × 81 × 161 grid. The five locations corresponding to (a) to (e) are θ = 0, 22.5°, 45°, 67.5°,and 90° respectively.
7.4 Pulsatile Flow in a Mechanical Heart Valve
The last numerical experiment is designed to demonstrate the capabilities of our method in a complex, pulsatile flow with moving immersed boundaries. We simulate physiological, pulsatile flow through a simplified bileaflet mechanical heart valve (MHV) mounted in a model aorta geometry. Bileaflet mechanical heart valves are widely used as prosthetic heart valves to replace malfunctioning native valves. However, all current mechanical heart valve designs are far from ideal and their implantation is associated with complications, such as thromboembolism, tissue overgrowth and anticoagulant related hemolysis, etc [37]. The exact mechanisms that lead to these undesirable complications are yet to be fully understood. They are, however, believed to be strongly linked with the complicated hemodynamics induced with the mechanical heart valve. As such, advancing our understanding of MHV flows through simulations is critical prerequisite for establishing and quantifying the link between complex hemodynamics and thromboembolic complications.
As shown in Fig. 17, the modeled aorta is basically a straight pipe (as opposed to the curved shape of the actual ascending aorta) with three bulges symmetrically attached to the side wall. These bulges are introduced to model the three anatomic dilations (triple-sinus structure) of the ascending aorta, which occur at the aortic root just above each one of the three leaflets of the native aortic valve. Even though the mechanical valve we consider herein is bileaflet, when it is implanted in the aortic position it operates just upstream a triple-sinus geometry very similar to that shown in Fig. 17. The diameter of the straight aorta is set equal to 25.4mm. A simplified bileaflet MHV that represents the geometry of a St. Jude Regent 23mm valve is inserted upstream to the triple sinus. The actual valve contains two leaflets and a circular ring like housing structure. The two leaflets are connected to the housing through a hinge mechanism and they open/close following the changing of incoming pulsatile flow waveform (as shown in Fig. 19). For the purpose of this paper, we neglect the housing structure as well as the hinge mechanism here and focus on the flow phenomena induced by the two moving leaflets. The background, empty aorta domain is discretized with a boundary-fitted, curvilinear grid system with 153 × 153 × 201 grid nodes along the two cross-sectional directions and the stream-wise direction, respectively (Fig. 18). The leaflets are discretized with an unstructured, triangular grid, immersed in the background mesh as shown in Fig. 18 and treated as sharp interfaces using the method of [1]. At the inlet we specify plug flow velocity profile whose magnitude varies in time according to the nearly physiological, half sine flow waveform shown in Fig. 19. The prescribed kinematics of the leaflet motion is also shown (dashed line) in Fig. 19 in terms of the relative position of leaflet (θ- θ0)/(θmax - θ0) (where θ is the leaflet opening angle and is defined as shown in Fig. 19 (b), θ0 and θmax represent the opening angle of the leaflet at the fully close and fully open position, respectively, and θ0 = 23° while θmax = 85°). The peak Reynolds number based on the peak flow velocity U and the aorta diameter is 4000, which is within the physiological range. The period of the flow cycle equals to 860ms and each cycle is divided into 1200 time steps. The typical convergence history of the Poisson equation solver is shown in Fig. 20. Even for this very complex flow case, which not only involves pulsatile flow but also rapidly moving immersed boundaries, our method can very efficiently reduce the discrete divergence of the velocity by up to 8 orders of magnitude within few iterations per simulated cycle.
Fig. 17.
The geometry for the straight aorta configuration with a anatomic-like triple sinus structure. (a) perspective view; (b) side view from the downstream direction.
Fig. 19.
(a). The prescribed incoming flow waveform and kinematics of leaflet motions for the mechanical heart valve case. (b) Definition of leaflet opening angle θ and θ0 (fully closed position), θmax (fully open position).
Fig. 18.
Representative views of the computational grid for the bileaflet mechanical heart valve simulation. (a) Side view showing the background curvilinear grid used to discretize the empty aorta and the unstructured mesh used to discretized the valve leaflets; (b) cross-sectional view. For clarity, only every third grid line is plotted.
Fig. 20.
Pulsatile flow through a bileaflet mechanical heart valve. Typical convergence rate for the discrete divergence of the velocity field over several instants in time during a simulated cardiac cycle. Empty aorta grid size: 153 × 153 × 201.
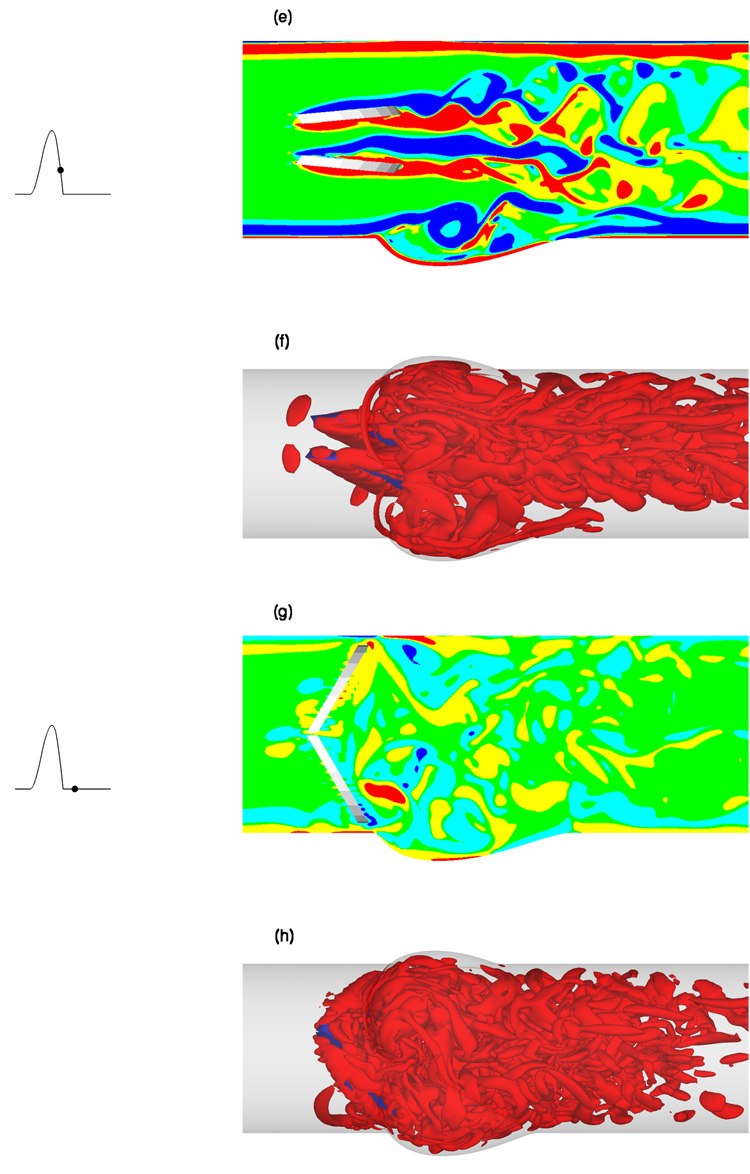
To illustrate the richness of the flow patterns generated by the moving leaflets, we show in Fig. 21 the numerical solutions at four different time instants, namely: (1) acceleration phase (Fig. 21 (a) and (b)); (2) peak systole (Fig. 21 (c) and (d)); (3) deceleration phase (Fig. 21 (e) and (f)); and (4) leaflets fully closed (Fig. 21 (g) and (h)). The calculated flowfields are visualized in terms of out-of-plane vorticity contours and the iso-surfaces of q-criterion [38]. The acceleration phase up to peak systole is dominated by the growth of coherent vortical structures shed from the valve leaflets and at the interface of the sinus and aortic flows. The non-linear interactions between these vortices leads to the rapid emergence of a very complex three-dimensional flow with multiple stream-wise and hairpin-like vortices. As the deceleration phase commences and the valve leaflets begin to close, the flow is getting rapidly disorganized and multiple small scale structures develop in the wake of the leaflets giving rise to a very rich, chaotic-like state.
Fig. 21.
Calculated instantaneous flow patterns for the pulsatile flow through a bileaflet mechanical heart valve. (a), (c), (e) and (g): Points indicate phases in the cardiac cycle. Middle: contours of the out-of-plane vorticity component on the vertical plane of symmetry of the valve leaflets. (b), (d), (f), and (h): Corresponding 3D coherent structures visualized using the q criterion [38].
It is evident from the above figures that the overall flow patterns generated by the moving leaflets of the MHV are very complex. The detailed discussion of the simulated flow physics, however, is beyond the scope of this work and will be reported in future publications. The results presented herein serve to illustrate the complexity of the flow in order to underscore the ability of our numerical method to obtain converged unsteady solutions for a dynamically rich, 3D, pulsatile flow case with moving immersed boundaries on a fine computational mesh.
8 Conclusions
We have developed a novel numerical method for solving the 3D, unsteady, Navier-Stokes equations in generalized curvilinear domains containing complex, moving, immersed boundaries. The method integrates elements from finite-volume, boundary conforming methods with a previously developed sharp-interface, Cartesian methodology for handling complex immersed boundaries. The method is especially suited for internal flow problems for which the background flow domain within which the moving boundaries are immersed can be efficiently discretized with boundary-fitted, generalized coordinates. Such situations are often encountered in simulations of cardiovascular flow problems where complex moving boundaries (the leaflets of a native or a prosthetic heart valve) are immersed within a blood vessel.
To develop the method we had to address two major numerical issues. The first issue relates to the development of a numerical technique for discretizing the Navier-Stokes equations in generalized, curvilinear staggered grids. The proposed discretization method is an extension to curvilinear coordinates of the hybrid staggered/non-staggered Cartesian grid method developed by Gilmanov and Sotiropoulos [1]. Our method is an improvement over currently available curvilinear, staggered grid techniques as it neither requires the explicit evaluation of the Christoffel symbols nor the discretization of all three Cartesian momentum equations at each surface center. The accuracy of the method on deliberately skewed and stretched curvilinear grids was demonstrated by applying to simulate flow in a lid-driven cavity. We showed that even on severely distorted curvilinear grids the method is capable of yielding solutions of comparable accuracy to those obtained on uniform Cartesian grids.
The second major issue we addressed in this work is the efficiency of the resulting unsteady flow solver on fine, curvilinear meshes. We employed a fractional-step approach coupled with a Jacobian-free, GMRES solver for the momentum step and a FGMRES method pre-conditioned with multigrid for the pressure-Poisson equation. We showed that when combined with a semi-coarsening strategy, the multigrid method is a powerful preconditioner of the FGMRES solver yielding convergence rates that are not very insensitive to grid size and aspect ratio. Numerical tests for impulsively started flow in a long straight duct and pulsatile flow in a curved pipe bend showed that the method can reduce the discrete divergence of the velocity field by 8 to 10 orders within 5 to 10 iterations on grids with 106 grid nodes.
The ability of the method to yield converged solutions for a very complex, pulsatile flow with moving immersed boundaries was demonstrated by applying it to simulate flow in a mechanical bileaflet heart valve mounted in a straight, albeit anatomically-inspired aorta geometry. The convergence rate of the flow solver even for this very complex case was comparable to that obtain in the simpler benchmark problems. The results demonstrate that our method can resolve geometrically complex flows with very rich flow physics and point to its potential as a powerful simulation tool for cardiovascular and other internal flow problems with moving, immersed boundaries.
Fig. 14.
Pulsatile flow in a 90 deg pipe bend. Measured (points) and computed stream-wise velocity profiles at t = 0.25T. Solid line: 81 × 81 × 81 grid; Dash line: 41 × 41 × 81 grid; Dash-dot line: 81 × 81 × 161 grid. The five locations corresponding to (a) to (e) are θ = 0, 22.5°, 45°, 67.5°,and 90° respectively.
Fig. 15.
Pulsatile flow in a 90 deg pipe bend. Measured (points) and computed stream-wise velocity profiles at t = 0.5T. Solid line: 81 × 81 × 81 grid; Dash line: 41 × 41 × 81 grid; Dash-dot line: 81 × 81 × 161 grid. The five locations corresponding to (a) to (e) are θ = 0, 22.5°, 45°, 67.5°,and 90° respectively.
Acknowledgements
This work was supported by NIH Grant RO1-HL-07262, NSF grant 0625976 and the Minnesota Supercomputing Institute. We are grateful to Ajit Yo-ganathan and the members of Georgia Tech’s Cardiovascular Fluid Mechanics Laboratory for providing us with the geometry of the mechanical valve and the leaflet kinematics.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Gilmanov A, Sotiropoulos F. A hybrid cartesian/immersed boundary method for simulating flows with 3d, geometrically complex, moving bodies. Journal of Computational Physics. 2005;207:457–492. [Google Scholar]
- 2.Peskin C. The immersed boundary method. Acta Numerica. 2003;11:479–517. [Google Scholar]
- 3.Ye T, Mittal R, Udaykumar HS, Shyy W. An accurate cartesian grid method for viscous incompressible flows with complex immersed boundaries. Journal of Computational Physics. 1999;156:209–240. [Google Scholar]
- 4.Udaykumar H, Mittal R, Rampunggoon P, Khanna A. A sharp interface Cartesian grid method for simulating flows with complex moving boundaries. Journal of Computational Physics. 2001;174(1):345–380. [Google Scholar]
- 5.Fadlun E, Verzicco R, Orlandi P, Mohd-Yusof J. Combined immmersed-boundary finite-difference methods for three-dimensional complex flow simulations. Journal of Computational Physics. 2000;161(1):35–60. [Google Scholar]
- 6.Kim J, Kim D, Choi H. An immersed-bounday finite-volume method for simulations of flow in complex geometries. Journal of Computational Physics. 2001;171:132–150. [Google Scholar]
- 7.Yang J, Balaras E. An embedded-boundary formulation for large-eddy simulation of turbulent flows interacting with moving boundaries. Journal of Computational Physics. 2006;215(1):12–40. [Google Scholar]
- 8.Fedkiw R, Aslam T, Merriman B, Osher S. A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the Ghost Fluid Method) Journal of Computational Physics. 1999;152(2):457–492. [Google Scholar]
- 9.Mittal R, Iaccarino G. Immersed boundary methods. Annual Review of Fluid Mechanics. 2005;37:239–261. [Google Scholar]
- 10.Zang Y, Street RL, Koseff R. A non-staggered grid, fractional step method for time-dependent incompressible Navier-Stokes equations in curvilinear coordinates. Journal of Computational Physics. 1994;114(1):18–33. [Google Scholar]
- 11.Wesseling P, Segal A, Kassels CGM. Computing flows on general three-dimensional nonsmooth staggered grids. Journal of Computational Physics. 1999;149:333–362. [Google Scholar]
- 12.Dwyer HA, Cheer AY, Rutaganira T, Shacheraghi N. Calculation of unsteady flows in curved pipes. Journal of Fluids Engineering. 2001;123(4):869–877. [Google Scholar]
- 13.Rindt CCM, van Steenhoven AA. Unsteady entrance flow in a 90° curved tube. Journal of Fluid Mechanics. 1991;226:445–474. [Google Scholar]
- 14.Harlow FH, Welch JE. Numerical calculation of time-dependent viscous incompressible flows with free surface. Physics of Fluids. 1965;8:2182–2189. [Google Scholar]
- 15.Maliska CR, Raithby GD. A method for computing three dimensional flows using non-orthogonal boundary-fitted co-ordinates. International Journal for Numerical Methods in Fluids. 1984;4(6):519–537. [Google Scholar]
- 16.Shyy W, Vu TC. On the adoption of velocity variable and grid system for fluid flow computation in curvilinear coordinates. Journal of Computational Physics. 1991;92:82. [Google Scholar]
- 17.Yang Z, Voke PR. Large-eddy simulation of boundary-layer separation and transition at a change of surface curvature. Journal of Fluid Mechanics. 2001;439:305–333. [Google Scholar]
- 18.Ko SC, Sung HJ. Large-eddy simulation of turbulent flow inside a sudden-expansion cylindrical chamber. Journal of Turbulence. 2002;3(1):4. [Google Scholar]
- 19.Rosenfeld M, Kwak D, Vinokur M. A fractional step solution method for the unsteady incompressible Navier-Stokes equations in generalized coordinate systems. Journal of Computational Physics. 1991;94(1):102–137. [Google Scholar]
- 20.He P, Salcudean M, Gartshore IS, Nowak P. Multigrid calculation of fluid flows in complex 3d geometries using curvilinear grids. Computers & Fluids. 1996;25(4):395–419. [Google Scholar]
- 21.Leonard BP. Stable and accurate convective modeling procedure based on quadratic upstream interpolation. Computer Methods in Applied Mechanics and Engineering. 1979;19(1):59–98. [Google Scholar]
- 22.van Kan J. A 2nd-order accurate pressure-correction scheme for viscous incompressible-flow. SIAM Journal on Scientific and Statistical Computing. 1986;7(3):870–891. [Google Scholar]
- 23.Beam RM, Warming RF. An implicit finite-difference algorithm for hyperbolic systems in conservation-law form. Journal of Computational Physics. 1976;22:87–110. [Google Scholar]
- 24.Knoll D, Keyes D. Jacobian-free Newton-Krylov methods: a survey of approaches and applications. Journal of Computational Physics. 2004;193(2):357–397. [Google Scholar]
- 25.Saad Y, Schultz M. GMRES: A generalized minimal residual algorithm for solving nonsymmetric linear systems. SIAM J. SCI. STAT. COMPUT. 1996;7(3):856–869. [Google Scholar]
- 26.Brown P, Saad Y. Hybrid Krylov methods for nonlinear-systems of equtions. SIAM Journal on Scientific and Statistical Computing. 1990;11(3):450–481. [Google Scholar]
- 27.Balay S, Buschelman K, Gropp WD, Kaushik D, Knepley MG, McInnes LC, Smith BF, Zhang H. PETSc Web page. 2001 http://www.mcs.anl.gov/petsc.
- 28.Buzbee BL, Golub GH, Nielson CW. Direct methods for solving poissons equations. SIAM Journal of Numerical Analysis. 1970;7(4):627–656. [Google Scholar]
- 29.Swarztrauber PN. A direct method for the discrete solution of separable elliptic equations. SIAM Journal on Numerical Analysis. 1974;11(6):1136–1150. [Google Scholar]
- 30.der Vorst H. BiCGSTAB: A fast and smoothly converging variant of BiCG for the solution of nonsymmetric linear systems. SIAM Journal of Scientific and Statistical Computing. 1992;13:631–644. [Google Scholar]
- 31.Saad Y. A flexible inner-outer preconditioned GMRES. SIAM Journal on Scientific Computing. 1993;14:461–469. [Google Scholar]
- 32.Barrett R, Berry M, Chan TF, Demmel J, et al. SIAM. Philadelphia, PA: 1994. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods. [Google Scholar]
- 33.Oosterlee C, Washio T. An Evaluation of Parallel Multigrid as a Solver and a Preconditioner for Singularly Perturbed Problems. SIAM Journal on Scientific Computing. 1998;19(1):87–110. [Google Scholar]
- 34.Trottenberg U, Oosterlee CW, Schuller A. Multigrid: Elsevier; 2001. [Google Scholar]
- 35.Ghia U, Ghia K, Shin C. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method, NASA, Symposium on Numerical Boundary Condition Procedures and Multigrid Methods, Moffett Field, CA, Oct. 19–22, 1981) Journal of Computational Physics (ISSN 0021-9991) 1982;48:387–411. [Google Scholar]
- 36.Healey TM. Ph.D. thesis. Georgia Institute of Technology; 2001. Multi-block and overset-block domain decomposition techniques for cardiovascular flow simulation. [Google Scholar]
- 37.Yoganathan AP, He Z, Jones SC. Fluid mechanics of heart valves. Annual Review of Biomedical Engineering. 2004;6:331–362. doi: 10.1146/annurev.bioeng.6.040803.140111. [DOI] [PubMed] [Google Scholar]
- 38.Hunt JCR, Wray A, Moin P. Eddies, stream, and convergence zones in turbulent flows. Tech. rep., Center for Turbulence Research Report CTR-S88. 1988