Abstract
A new optimization-based method is presented to predict the hydrophobic residue contacts in α-helical proteins. The proposed approach uses a high resolution distance dependent force field to calculate the interaction energy between different residues of a protein. The formulation predicts the hydrophobic contacts by minimizing the sum of these contact energies. These residue contacts are highly useful in narrowing down the conformational space searched by protein structure prediction algorithms. The proposed algorithm also offers the algorithmic advantage of producing a rank ordered list of the best contact sets. This model was tested on four independent α-helical protein test sets and was found to perform very well. The average accuracy of the predictions (separated by at least six residues) obtained using the presented method was approximately 66% for single domain proteins. The average true positive and false positive distances were also calculated for each protein test set and they are 8.87 Å and 14.67 Å respectively.
1 Introduction
Protein structure prediction is one of the greatest challenges in the field of computational biology. A variety of techniques are employed to make such predictions (comparative modeling, fold recognition and first principle based methods)(Floudas et al., 2006; Floudas, 2007). A first principles based approach is the most difficult type because such methods do not use information from the database of proteins with known structures. These methods rely on a search of the conformational space of a protein to find energetically stable and physically realizable structures. The use of additional restraints based on known or predicted tertiary contacts can be used to guide the search and help a structure prediction algorithm identify better quality structures. The definition of a contact is method dependent and a contact is said to occur when two atoms/residues are in spatial proximity with each other. The definition of a contact can be based on the distance between two Cα atoms, or between two Cβ atoms or may be a combination of both (Fariselli et al., 2001b). These predicted contacts can then be explicitly used as restraints in structure prediction algorithms. Contact prediction methods can also be enhanced and used for secondary structure topology and disulfide bridge prediction. Thus, the development of an effective residue contact prediction model can play a vital role in protein structure prediction (Ortiz et al., 1998a,b, c; Olmea et al., 1999; Cheng and Baldi, 2006; Bonneau et al., 2002; McAllister et al., 2006; McAllister and Floudas, 2007). Ortiz et al. (1998a) used multiple sequence alignments to derive distance restraints that were used in Monte Carlo simulations. Similarly, McAllister et al. (2006) integrated their α-helical topology prediction method with an ab-initio protein structure prediction method ASTRO-FOLD (Klepeis and Floudas, 2003c).
Various research groups have introduced different approaches to develop residue contact prediction methods (Horner et al., 2008; Cheng and Baldi, 2007; Vicatos and Kaznessis, 2008; Shackelford and Karplus, 2007; Vullo et al., 2006; Kundrotas and Alexov, 2006; Vicatos et al., 2005; Punta and Rost, 2005; Zhang and Huang, 2004; Zhao and Karypis, 2003; Shao and Bystroff, 2003; Singer et al., 2002; Fariselli et al., 2001a; Fariselli and Casadio, 1999; Lund et al., 1997; Göobel et al., 1994). These methods can broadly be classified into two categories. The first category uses correlated mutations analysis and the second category uses machine learning techniques for contact prediction. There exist a variety of machine learning approaches like hidden Markov models, self organizing maps and support vector machines (Zhao and Karypis, 2003; Cheng and Baldi, 2007) that are used for protein residue contact prediction. A few selected publications using these methods are reported below. Several researchers have specifically investigated the disulfide bridge connectivity and its relationship with protein structures (Chuang et al., 2003; Cheng et al., 2006; Chen and Hwang, 2005; Rubinstein and Fiser, 2008).
Correlated mutations analysis is based on the premise that mutations in proximal residues occur in a covariant fashion (Vicatos et al., 2005). This means that when a critical residue (i.e., important for protein function) of a protein is mutated, the proximal residues are likely to undergo mutations in order to keep the functionality intact (Vicatos et al., 2005). This hypothesis has been used as the underlying principle for various correlated mutations based contact prediction methods. Hamilton et al. (2004) used neural networks on a training set of 100 proteins. Instead of using pairwise correlation as the predictor, they used windows (pairwise correlation between 5 residues centered around a residue of interest) of correlation for contact prediction and reported an improved accuracy. This method resulted in an overall accuracy value of 30.7% when the best L/10 predictions are considered. Fariselli et al. (2001b) also used a correlated mutations analysis approach with neural networks and reported that their method had the lowest predictive ability for α-helical proteins relative to proteins of different structural classes. A similar result was also reported in another publication (Vicatos et al., 2005). Vicatos et al. (2005) started with a vector of 142 descriptors (based on the physiochemical properties) that they used for residue similarity comparison. These 142 descriptors are subsequently reduced to a set of 19 descriptors using Principal Component Analysis. Finally a set of 3 main descriptors was selected for correlated mutations analysis. This method was tested on all protein structural classes and was found to produce an average accuracy of around 15% using their two predictors for α-helical proteins. In another work, Vicatos and Kaznessis (2008) proposed a Monte Carlo simulation based approach to separate true positive predictions from the false positive predictions and thus increasing the accuracy of predictions for α-helical proteins.
In a recent work, Cheng and Baldi (2007) proposed a support vector machine method (SVMcon) to address this problem. This method uses a set of five features (local window feature, pairwise information feature, residue type feature, central segment window feature, and protein information feature) as input to predict the likelihood of contact between two residues (Cheng and Baldi, 2007). The use of the enhanced feature set enabled to authors to attain a higher level of accuracy and coverage on the test set. SVMcon was also tested on all protein structural classes and an average accuracy of 24% 17%, and 11% was obtained for α-helical proteins for residue separation value of 6, 12, and 24, respectively.
Despite all these developments, the protein residue contact prediction problem has still not achieved a desired level of success. There has been a conscious effort by re-searchers in this field to address this problem, which is also part of the Critical Assessment of Techniques for Protein Structure Prediction (CASP) experiments (Grana et al., 2005). As mentioned earlier, it has been found that predicting non-local contacts in α-helical proteins is a relatively difficult problem relative to predicting contacts in other structural classes of a protein (MacCallum, 2004). Our proposed method specifically aims at predicting non-local hydrophobic contacts in α-helical proteins and our focus is on improving accuracy of the predicted hydrophobic contacts. A complete description of the proposed model is presented in the following sections.
2 Methods
The residue contact prediction model in this article aims at predicting the contacts between different hydrophobic residues of an α-helical protein which can be used to narrow down the space searched by protein structure prediction algorithms. This contact prediction model is based on Anfinsen ‘s hypothesis (Anfinsen, 1973), which states that for a given physiological set of conditions the native structure of a protein corresponds to the global Gibbs free energy minima. The proposed model also selects contacts in such a way that the total energy of such a configuration is minimum. Given the secondary structure information (location of α-helices) of an α-helical protein, the proposed integer linear optimization model predicts a set of residues that are most likely to form contacts (i.e., interhelical contacts between hydrophobic residues). This method also produces a distance range in which these predicted contacts are most likely to occur. It uses the information about secondary structure of a protein as input to the model. The secondary structure information is obtained using the Dictionary of Protein Secondary Structure (DSSP)(Kabsch and Sander, 1983). The DSSP method assigns secondary structure through the identification of hydrogen bonding patterns indicative of α-helices, β-sheets, and turns. A high resolution Cα-Cα distance dependent force field (Rajgaria et al., 2006) is used to calculate the interaction energy between different residues of a protein. This force field is discussed in detail in Section 2.1. The energy of the conformer is calculated using this force field and the contacts that produce the lowest energy (that also satisfy some structural constraints) are selected by the proposed integer linear optimization model. Problem specific constraints can be easily incorporated in the existing model. This method has been found to perform very well on four different protein test sets with a very good accuracy.
2.1 High Resolution Cα-Cα Distance Dependent Force Field
The force field used in this formulation is a high resolution Cα-Cα distance dependent force field generated using a linear optimization formulation (Rajgaria et al., 2006). The force field is denoted as high resolution because it has been trained on a large set of high resolution decoys (small rmsd with respect to the native) and it was generated by requiring that the native structure always has a lower energy value than the similar non-native structures. This type of training ensures that the force field will assign a contact energy that would result in a lower energy configuration.
The Cα-Cα high resolution force field (HRFF) is a distance dependent force field and the energy of an interaction between two residues depends on the “contact” distance between the two Cα atoms. A contact exists when the Cα carbons of two amino acids are within 3 and 9 Å of each other. Hence, the energy of each interaction is a function of the Cα-Cα distances and the identity of the interacting amino acids. For 20 naturally occurring amino acids, there are 210 amino acid combinations and for 8 distance bins (refer Table I) there are 1680 energy parameters. In this model these energy parameters are denoted as Ei,j,b, where i and j are the interacting amino acids and b is the contact distance. The Cα-Cα HRFF is then simply used as a lookup table and the interaction energy between any two amino acids of given identities and distance is a parameter. For more detailed information on force field generation, readers are referred to the original work (Rajgaria et al., 2006).
Table I.
Distance dependent contact range definition based on predicted bin.
| Bin ID | Predicted Cα-Cα Contact Distance Range [Å] |
|---|---|
| 1 | 3.0–8.0 |
| 2 | 3.0–9.0 |
| 3 | 3.0–10.0 |
| 4 | 3.0–11.0 |
| 5 | 4.0–12.0 |
| 6 | 4.0–12.0 |
| 7 | 4.0–12.0 |
| 8 | 4.0–12.0 |
2.2 Optimization Model Formulation
A binary variable, wi,j,b is defined for each residue pair and this variable is active only when the pair (I, j) forms a residue contact in the given distance bin b. The high resolution force field uses 8-bin distance definition for the interaction energy between two interacting amino acids. These bins range from 3.0 Å to 9.0 Å. Contacts beyond this range are assumed to not contribute to the energy of a conformer. The model uses an extra bin, bin 9, to identify these no-contacts.
Table I shows the relation between the contact bin and the predicted contact distance range in which the predicted contact is likely to occur. From this table it can be seen that there is no prediction for distances less than 3.0 Å. It is very rare for two Cα atoms of two different residues to come closer than 3.0 Å, therefore predicted contacts are always more than 3.0 Å. A maximum prediction width of 8.0 Å is used to define a contact. If a contact is predicted in bin 1, then it means that the distance range of this contact varies from 3.0–8.0 Å. Similarly, for other bins the predicted contact distance range is given in column 2 of Table I.
Using the contact energy values, this formulation then identifies the optimal contact bin (bin 1–8 if there is a contact and bin 9 if there is no contact) for each residue combination subject to a set of constraints. These constraints are an important part of the formulation and are included either as a preprocessing step or as model equations (refer Section 2.3 and 2.4). In the preprocessing step some of the contacts are fixed before the model is solved. Model equations are constraints that are enforced while the solver searches the solution space. These constraints are described in Section 2.3 and Section 2.4.
2.3 Objective function and contact variables
The objective function of this formulation is to predict the set of hydrophobic residue contacts of a protein that minimizes the contact energy. In this formulation, every active binary variable, wi,j,b (representing the existence of a residue-residue contact between pair i, j at distance bin b) contributes to the energy of a conformer by amount Ei,j,b. The high resolution distance dependent force field published in Rajgaria et al. (2006) is used as the energy parameter for bins 1–8. It has been observed from the force field plots that as the contact distance increases, (greater than 9 Å) the interaction energy approaches a value of 0 for most of the residues. For this reason, the energy value of bin ‘9’ (which represents no contact), is assigned as zero (Ei,j,9 = 0).
The objective function can be written in terms of the binary variables and parameters as Equation 1. As mentioned earlier, whenever there is a contact between residue pair (i, j) at a distance bin b, then this contact contributes to the energy of a protein by amount Ei,j,b. Thus, the total energy of a protein can be calculated by taking the sum of such energy contributions over all residue pairs (Equation 1). Also, a residue pair (i, j) can only form contact in one of the 9 bins. This means that wi,j,b will be equal to 1 for only one bin b and it will be equal to 0 for rest of the bins. This is incorporated in the model as Equation 2. A binary variable yci,j is defined for each residue pair and this variable is active only when the pair (i, j) forms a residue contact in the first 8 bins. Equation 3 relates the activity of variable yci,j to wi,j,b. yci,j is equal to 1 when there is a contact between residue pairs (i, j) in bin 1–8. If the contact occurs in the last bin (bin 9) then yci,j is set equal to 0.
| (1) |
| (2) |
| (3) |
It might appear that the total energy in Equation 1 is calculated by summing the contribution from all possible residue pairs i and j, and not just hydrophobic residues. However, as explained later in the text (refer Section 2.4.2), all binary variables yci,j, corresponding to non-local (residues separated by more than 5 residues), non-hydrophobic contacts are set equal to zero. Thus, these non-local, non-hydrophobic contacts do not contribute to the total energy of the conformer. However, local non-hydrophobic residues are allowed to make contacts.
2.3.1 Helix Contact Constraints
For every helical residue hi (i ∈ α – helix), Equation 4 establishes the maximum number of non-local contacts that can be specified using hi. This constraint is included in order to limit the number of contacts a helical residue can have. Equation 4 means that every helical residue i, can at most make three contacts with other helical residues j that are not in the same helix and that are separated by at least three residues from i. This local separation of three residues is introduced to discount the contacts that a residue would make with other local residues because of sequential proximity. Increasing the right hand side value from three to four will produce more predictions but all of these predictions might not be correct or most effective. Similarly, decreasing the value of right hand side to two will result in a smaller subset of contacts while possibly missing some important contacts.
Equation 5 is a similar version of Equation 4 for helical residues that are Cysteine. Cysteine residues are also involved in forming disulfide bridges with other Cysteine residues of a protein. This additional contact property of Cysteine residues is included by allowing four non-local contacts for each of the helical Cysteine residue in a protein.
| (4) |
| (5) |
Another binary variable yhp,q, is introduced to represent a contact between two helices p and q. If any residue of helix p makes a contact with any residue of helix q, then this variable is active (i.e., yhp,q=1) implying a contact between these two helices. Thus, if wi,j,b is active for a residue pair (i, j) where i and j are residues of two different helices (p and q) and b is in the first 8 bins (denoting a contact) then yhp,q is forced to be active. This condition is written in the form of Equation 6. Similarly, if helices p and q are contacting each other then there should be at least one active contact between the residues of helix p and helix q. This constraint is included by relating the variable yhp,q to variable wi,j,b in the form of Equation 7.
| (6) |
| (7) |
Equation 8 is included in the model to limit the maximum number of interactions a helix can have with other helices of the protein. In the proposed model, a helix is only allowed to contact two other helices. This limit on the maximum number of helical contacts can be changed but a maximum value of two was set as an upper limit in order to require that the model choose the most important contacts.
| (8) |
Equation 9 requires that when two non-local, interhelical hydrophobic residues hi and hj (hi: subset of residues i which are in a helix; hi and hj are alias of each other) form a contact then hi, hj + 2 should not form a contact in bins 1–6. This equation is motivated from the fact that residues hj and hj + 2 do not lie on the same side of a helix. If there exists a contact between hi and hj, then the contact between hi and hj + 2 should be in bin 7 or bin 8. This constraint is written in terms of Equation 9. For the cases when hi and hj form a contact, ychi,hk equals 1 and the right hand side of this equation becomes 0 forcing all whi,hj+2,b (for bins 1–6) to take a value of zero.
| (9) |
It was observed that when a small helix (less than six residues) is connected to two other helices (one on either side) by long loops then the smaller helix rarely contacts adjacent helices. This constraint was included in the model in the form of Equation 10. In this equation, helbeg(p) − helend(p−1) − 1 denotes the loop length between helix hp and helix hp−1. Similarly, helbeg(p+1)−helend(p)−1 denotes the loop length between helix hp+1 and helix hp.
| (10) |
Another set of constraints is added to fix some of the contacts based on the parallel and anti-parallel topology of consecutive and non-consecutive helices. Two consecutive helices can be either in a parallel or an anti-parallel arrangement (except for a few orthogonal arrangements). The four most common possible arrangements for two contacting helices are shown in Figure 1. The first two arrangements (AP1 and AP2) correspond to the anti-parallel arrangement. AP1 corresponds to the case where the beginning of first helix is in contact with the end of the second helix and AP2 corresponds to the arrangement where the end of the first helix is in contact with the beginning of the second helix. Similar arrangements for parallel helices are denoted by P1 and P2.
Figure 1.
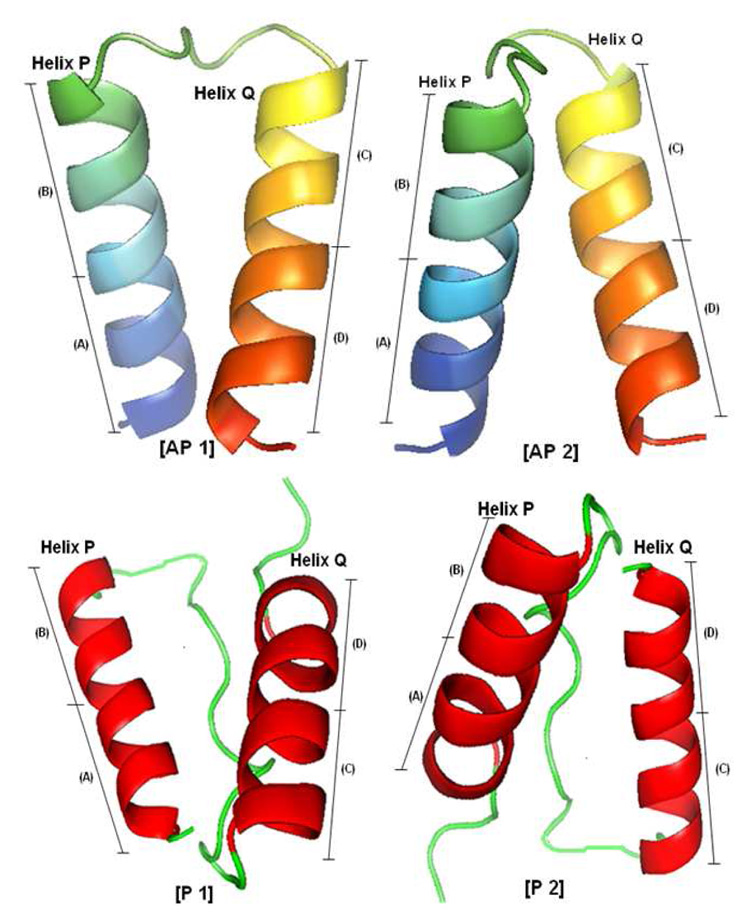
Four possible anti-parallel and parallel arrangements for consecutive helices. The top 2 arrangements denoted by AP1 and AP2 are anti-parallel arrangements and the bottom 2 arrangements denoted by P1 and P2 are parallel arrangements. Each contacting helix can be divided in two parts (A and B for helix P; C and D for helix Q). AP1 occurs when part A of helix P contacts part D of helix Q. Similarly, AP2, P1, and P2 occur when B–C, A–C and B–D contacts take place.
The occurrence of one of these arrangements depends on the length of the intermediate loop and the length of contacting helices. To better understand the length dependence, a set of 317 α-helical proteins was studied. There were 1764 consecutive α-helices in this set. In this study, the length of the intermediate loop along with the length of consecutive helices for each of these α-helical proteins was recorded. It was observed that for cases where the loop length was less than three residues, the AP2 arrangement occurred in about ~ 85 % cases. The small intermediate loop prohibits other arrangements to take place and because of this the end of first helix contacts the beginning of second helix resulting in an AP2 configuration.
For cases where the loop length was less than or equal to 6 residues, the anti-parallel arrangement was much more common than the parallel arrangement. The ratio between the loop length and the length of the smaller helix was calculated for these cases and it was found that when the loop length was less than or equal to six residues and the loopratio was less than 0.75 then AP2 arrangement occurred most of the time. Here, len(help) and len(helq) denote the length of helix p and q, respectively. These observations were used as constraints in our model to predict AP2 arrangements for above mentioned cases.
Equation 11 requires that when two consecutive helices are separated by three or less loop residues, then the helices must contact each other. Equations 12 and 13 are enforced for cases where the loop length is less than or equal to 6 residues and the loopratio is less than 0.75. These two equations require the contacting helices to have an AP2 contact arrangement. The AP2 arrangement is enforced by only allowing contacts between part B of helix p and part C of helix q (Figure 1). The binary variables denoting the contact between part A of helix p and helix q are set to zero. Similarly, binary variables denoting the contact between helix p and part D of helix q are also set to zero (as shown in Equation 13).
| (11) |
| (12) |
| (13) |
However, Equations 12 and 13 are only enforced when two contacting helices have comparable length. If the length of one helix is more than the double of another helix then the smaller helix is allowed to make contact with all residues of the longer helix. This constraint is incorporated for the cases shown in Figure 2. This constraint is written in the form of Equation 14 and 15.
| (14) |
| (15) |
Figure 2.

Cartoon depicting one scenario of a contact between two helices of different length. The length of helix P is very small compared to the length of helix Q. Under these circumstances it is possible for the smaller helix to contact the full length of the bigger helix.
For cases where the intermediate loop length is more than 7 residues (for consecutive and non-consecutive helices), no specific arrangement is enforced thus allowing the formulation to choose one of these arrangements (if contacting) based on the resulting energetic contribution. However, if two helices are in contact then it is enforced that the contacts occur in only one of these types of arrangements.
It was also observed that if the first and last helix of a protein contact, they contact in an anti-parallel fashion. This is natural to expect because a parallel arrangement would force the beginning and end loops (N-terminal and C-terminal coils) to go in opposite direction. This observation was investigated using a test set of 317 α-helical proteins. The average Cα-Cα distance between the first three and last three residues of first and last helix was calculated for each of these α-helical proteins. These four average distances were used to determine the four possible arrangements of these helices (Figure 1). The helices were said to be in contact when the average distance for one of these configurations was less than 9 Å. In this set, a total of 17 cases were found where first and last helices were contacting. Out of these 17 cases, the first and last helix contacted in an anti-parallel fashion 16 times. There was only one case in which the first and last helix contacted in a parallel fashion. This observation was written as a constraint in the form of Equation 16, which says that if there is a contact between the first and last helix of a protein then it should not be in a parallel fashion. Here, yhP(p,q) is a binary variable denoting the contact between helix p and helix q in a parallel fashion.
| (16) |
2.3.2 Loop And Coil Contact Constraints
This set of constraints is motivated from the fact that modeling a loop is very difficult and in the absence of such constraints the loop residues are free to make any contacts. These unrestricted non-local contacts can prohibit some of the important critical contacts resulting in a completely different topology. Equation 17 requires that the beginning and the end loop (N-terminal and C-terminal coils) of a protein do not form any non-local contact.
| (17) |
A similar equation can be written for the loop residues (other than the N-terminal and C-terminal coil residues) to prohibit non-local contacts. In the proposed model this constraint has been included as a preprocessing step (as shown in Equation 35).
2.3.3 General Contact Constraints
Equations 18 and 19 require that no three consecutive contacts should take place in the same bin. This equation is motivated from the observation that it is not very common to find three consecutive residues forming contacts with a common residue at approximately same distance. Although, it is possible to find such uncommon occurrences, this model aims at predicting typical (common) contacts using a mathematically rigorous framework.
| (18) |
| (19) |
The following three equations correspond to Cystine residues of a protein. It is expected that one Cystine residue will be part of at most one disulfide bridge. It has also been observed that the distance between two disulfide bridge forming Cystine residues is always below 6.5 Å. Equation 20 illustrates this constraint.
| (20) |
When two Cysteine residues participate in a disulfide bridge formation then it has been observed that the neighboring residues also form contacts because of spatial proximity between the participating cysteine residues. Thus, whenever a disulfide bridge is formed between residue i and j, then there should exist at least one contact in the neighborhood of both residues i and j. Equation 21 and 22 illustrate this constraint.
| (21) |
| (22) |
2.3.4 Integer Cut Constraints
This optimization based formulation offers a great advantage of generating multiple solutions. A single solution obtained using this formulation corresponds to the one with the lowest contact energy. However, it is possible to generate a rank-ordered list of solutions by using the following integer cut constraint (Equation 23). The addition of this constraint allows the user to generate a specified number of contact results in increasing order of optimal value (the objective function is being minimized). This ability to generate a rank ordered list of results in a mathematically rigorous way adds to the algorithmic advantage of the model.
| (23) |
Set A in Equation 23 represents the set of all active yhp,q (i.e., yhp,q = 1) variables. The cardinality of set A, card(A), is the total number of elements in set A. I represents the set of inactive variables. The use of Equation 23 excludes the previous solution from the feasible solution space for every subsequent iteration and a unique solution is obtained for each of the iterations.
2.4 Preprocessing Constraints
The preprocessing step helps reduce the search space of the contact prediction problem by fixing some of the contacts that one is most certain about. This type of information can be obtained by observing and rigorously quantifying the distances between various residues of a protein (i.e., intrahelical distances).
In order to obtain a representative set of protein structure tendencies, a large set of non-homologous protein structures that span the Protein Data Bank (Berman et al., 2000) should be selected. For this implementation, a set of structures that contain no more than 25% sequence similarity, denoted as PDBselect25, (Hobohm and Sander, 1994) has been used to develop the distance and angle bounds based on geometric tendencies. This PDBselect25 data set contains 2216 proteins and a total of 352,855 residues. Distance bounds are derived by observing the distances between residues in different secondary structures of a protein.
Some of these observations for intrahelical contacts are included in the Figure 3. The rest of the figures depicting occurrences of intrahelical distances are presented in Appendix 1. Figure 3 considers the distribution of contact distance between a helical residue, hi and, hi+3. This plot shows the distances that commonly occur for residues separated by 3 positions within a helix. A single peak distribution of distance occurrences is clearly visible. In this case, a lower bound of 4 Å and an upper bound of 6.0 Å appears to be appropriate to capture the typical intrahelical hi, hi + 3 distance for protein structures. Similarly, distance bound for hi, hi+4, hi+5 can be obtained from Figure 3. These observations are included as preprocessing constraints as mentioned in Section 2.4.2.
Figure 3.

Distribution of distance occurrences for intrahelical distances within the PDBse-lect25 data set.
The constraints included as a preprocessing step may not always be valid for all proteins. However, the aim here is to realistically approximate the geometry of protein interactions in a linear fashion. These preprocessing steps are discussed below.
2.4.1 General Constraints
It has been observed that the distance between residue i and i + 1 is limited to the range of 3.0–4.0 Å. This information is used as a preprocessing step to fix all the binary variables associated with this type of contact. This preprocessing is written in terms of Equation 24. Similarly, Equations 25 and 26 are also included as a preprocessing step to fix the binary variables corresponding to i, i+2 and i, i+3 contacts for each residue of a protein.
| (24) |
| (25) |
| (26) |
2.4.2 Helix Specific Constraints
The following set of constraints correspond to intrahelical contacts. These constraints are included to enforce the observed contact distances between various intrahelical residues, as shown in Figure 3. From this figure it can be seen that in most of the cases, the intrahelical contact distance between residues hi and hi + 3 of a helix is in between 4.0–6.0 Å. This observation can be used to restrict binary variables that denote a contact between an intrahelical pair hi and hi+3 beyond this contact distance range (Equation 26). Similarly, the most likely intrahelical contact distance range for residue pair hi and hi + 4 is 5.5–7.0 Å. This observation is also used to fix binary variables corresponding to bin 1–3,7–9 for intrahelical pair hi and hi + 4 (Equation 28). A similar constraint can be derived using Figure 3 for contact distance between intrahelical residue pair hi, hi + 5 (Equation 30). Intrahelical contacts that are separated by 6 or more residues are always more than 9 Å(bin 9). This observation is included in the form of Equation 30.
| (27) |
| (28) |
| (29) |
| (30) |
It is also desirable to fix the distance range in which two different helices interact (interhelical contacts). It has been observed that the contact distance between residues of two neighboring helices is rarely less than 6 Å. For non-neighboring helices we impose a minimum distance cutoff of 6.5 Å. These constraints are included as a preprocessing step (Equations 31 and 32) to fix all the binary variables denoting contact between two helical residues below 6 Å and 6.5 Å, respectively.
| (31) |
| (32) |
Equation 34 limits the contact between two interhelical residues, hi and hj based on their hydrophobic identity. The following set of residues, ℋ, are considered to be hydrophobic :
| (33) |
A parameter ifHP(hi) is defined for each of the helical residue hi. This parameter is equal to one when the residue is a hydrophobic residue (Equation 33) and is equal to zero otherwise. Two non-local (separated by more than 5 residues) interhelical residues are allowed to form a contact (bin 1–8) only when both residues belong to the hydrophobic residue set as given in Equation 33. This is an important preprocessing step because it sets all the binary variables corresponding to interhelical, non-hydrophobic contacts equal to zero. Thus, the proposed model only predicts hydrophobic contacts between two interacting helices.
| (34) |
2.4.3 Loop Specific Constraints
In the proposed model, we limit the contacts that any loop residue can have by allowing only local contacts. For any loop residue i, contacts are only allowed with residue (i−2, i−1, i+1, and i+2). However, if loop residue i, is Cysteine, then this constraint is not applied (to allow for the disulfide bride formation). This constraint is illustrated in Equation 35.
| (35) |
2.4.4 Helix and Sheet Specific Constraints
This subsection discusses the preprocessing steps that are included to limit the interaction between an α-helical residue hi, and a β-strand residue sj. Although this model has been specifically developed for α-helical proteins, some constraints and variables denoting contact between helical and strand residues have also been included. Inclusion of these constraints makes the model applicable for cases where a protein is primarily an α-helical protein but also has a small percentage of β-strand residues. An enhanced model to address α-β, and β proteins is being developed and will be part of a future publication.
Equation 36 requires that a contact between a helical and a strand residue that are separated by less than 4 residues (local contact) should not occur below a distance of 6 Å. A similar equation (Eq 37) is included to restrict the non-local contacts between such residues. Equation 37 requires that non-local residues (residue separation more than 4) of a helix and a strand should always occur in bin 9. These equations are not applied if both the interacting residues are Cysteine.
| (36) |
| (37) |
3 Sequence similarity
To evaluate the effect of sequence identity on the test results, sequence similarity was calculated between the 1250 Cα-Cα HRFF training proteins and the four test sets used in this work. PISCES, a method to identify a list of sequences with a maximum allowable sequence identity, was used (Wang and Dunbrack(Jr.), 2003). A maximum allowable sequence identity of 35% was used for all of these comparisons.
To calculate the sequence similarity between the Cα-Cα HRFF training and test set 1 (Cheng and Baldi, 2007), an-all-against all comparison was performed. For test set 1 (11 α-helical proteins), 11 × 1250 = 13750 comparisons were performed. Out of these 13750 comparisons, There was only one pair of proteins with sequence identity greater than 35%. A similar calculation was performed for the test set 2 (25 α-helical proteins) (Vicatos et al., 2005). For these 25 proteins, a total of 25 × 1250 = 31250 comparisons were performed and no pair of proteins had sequence identity more than 35%. Similarly, none of the proteins from test set 3 (25 α-helical proteins) and test set 4 (20 α-helical proteins) had sequence identity more than 35% when compared with the HRFF training proteins. Thus, there is no sequence similarity between the Cα-Cα HRFF training set and the test sets used in this work for a similarity threshold of 35%.
Sequence similarity was also calculated for the 317 α-helical proteins that were used to establish helix contact constraints (Section 2.3.1). The sequence similarity between these 317 proteins and all test proteins were calculated to estimate a possible bias (if any) in the results. All against all sequence similarity comparison was performed between all the 81 test proteins (test set 1- test set 4) and the set of 317 proteins. Out of these 317 × 81 = 25677 comparisons, there were only 7 proteins pairs with sequence identity greater than 35%.
4 Results and Discussion
An integer linear optimization model was developed to find the hydrophobic contacts between different residues of a protein. These predicted contacts can be used as explicit constraints in protein structure prediction methods to narrow down the search space thereby generating more realistic and accurate structures. The objective function of this formulation is to minimize the sum of contact energies while satisfying a set of constraints that were included in the model. These constraints were written as either a preprocessing step or model equations and were included in the model to produce physically realistic solutions. A high resolution Cα-Cα distance dependent force field (Rajgaria et al., 2006) was used to calculate the contact energy between different residues. This force field was generated by requiring that the native structure of a protein always has lower energy than the near-native structures of the same protein. Minimizing contact energy based on this force field should result in contacts that mimic the native structures. Integer cut constraints were also used to generate a rank-ordered list of contact predictions. About 3–5 predictions were obtained for each of the test cases. In most of the cases, the best prediction was in the top three predictions.
The effectiveness of a contact prediction can be measured by calculating its accuracy. Accuracy is defined as the ratio of correct predictions to total predictions. Accuracy can also be defined in terms of true positives (TP) and false positives (FP) as shown in Equation 38. It can be seen from Equation 38 that the higher the value of accuracy, the better the contact prediction model becomes.
| (38) |
| (39) |
Another metric used to measure the performance of contact prediction method is coverage (Equation 39). Coverage is defined as the ratio of correct predictions to the number of contacts in the native structure. A high coverage value means that the model is capable of predicting most of the contacts of a protein. To calculate accuracy, all the predicted contacts were compared with the native contacts. If the predicted contact was within the distance range corresponding to the actual native contact [as given in Table I] then the contact is counted as a true positive or correct contact. Otherwise the contact is considered a false positive. The total number of true positives is then divided by total number of predicted contacts to calculate accuracy. Coverage is calculated by taking the ratio of true positives to the total number of native contacts.
A high value of both accuracy and coverage is expected from a good contact prediction method. However, good accuracy does not mean good coverage and vice versa. Since, the current approach only predicts the hydrophobic contacts, coverage is not important for this approach. The proposed method was developed with the aim to produce higher accuracy. We believe that even a few good (true) contacts can help a structure prediction method produce good protein structures. Thus, the constraints that are part of the present formulation were written with the aim to produce accurate contacts even if it meant disallowing some of the native contacts (hence producing a low coverage value). For example, if we allow the number of permissible contacts for each helical residue hi, to be from 3 to 4, then the coverage of predicted contacts will increase while decreasing the accuracy of the contacts. Similarly, reducing the number of permissible contacts might increase the accuracy at the expense of reduced coverage. Hence, the proposed method also offers the flexibility of optimizing one of the two goals by varying the right hand side of constraint equations. This method was tested on α-helical proteins of four independent test sets. The testing results and comparisons on all these test sets are presented in following subsections.
4.1 Protein Test Set 1
The first test set was taken from the recent work by Cheng and Baldi (2007). In this work, the authors developed a residue contact prediction method (SVMcon) using Support Vector Machines. This method uses a set of five input features. Using these feature sets, the method then uses Support Vector Machines to predict if a pair of residue forms a contact. A contact is said to have occurred if the distance between the Cα atoms of two residues are less than 8 Å. If the distance between the Cα atoms of two residues is more than 8 Å then these residues are said to have no contact. This method then analyzes the prediction results in terms of non-local contacts that are 6, 12, and 18 residues apart. SVMcon performs best for the contacts that are 12 residues apart.
Cheng and Baldi (2007) tested SVMcon on a set of 48 proteins covering all SCOP (Murzin et al., 1995) structural classes. Our proposed method was only tested with the α-helical proteins of their test set. There are 11 α-helical proteins in this test set with protein lengths varying from 52 to 190 residues. Our prediction results on this test set are presented in Table II. Table II presents the performance of our method for 11 α-helical proteins for residue separation of 6, 12 and 24 residues. The third column reports the accuracy of our method for predicted residue contacts that are 6 residues apart. The number of true positive contacts (TP) and total contacts (TP+FP) are also listed in column three of this table. The average accuracy of the proposed method is 0.706. The highest and lowest value of accuracy was obtained for protein 1ELRA and 1ECAA, respectively. The average value of coverage for these 11 test proteins was also calculated (not shown in Table II). For residue separation value of 6 the average coverage value was 0.287. For α-helical proteins, Cheng and Baldi (2007) reported an average 0.24 for both accuracy and coverage for residue separation of 6 or more residues.
Table II.
Residue contact prediction results when tested on 11 α-helical test proteins of test set 1. (Cheng and Baldi, 2007)
| Residue Separation =6 | Residue Separation =12 | Residue Separation =24 | ||||
|---|---|---|---|---|---|---|
| PDB ID | Length | Accuracy | AvgTPdis | AvgFPdis | Accuracy | Accuracy |
| 1IG5A | 75 | 0.969(31/32) | 8.9 | 12.6 | 0.963(26/27) | 1.000(12/12) |
| 1HXIA | 108 | 0.824(14/17) | 8.3 | 14.4 | 0.818(9/11) | NA (0/0) |
| 1SKNP | 74 | 0.417(5/12) | 10.1 | 14.2 | 0.333(3/9) | NA(0/0) |
| 1ELRA | 128 | 0.971(33/34) | 8.8 | 12.6 | 1.000(11/11) | NA(0/0) |
| 1E29A | 135 | 0.714(15/21) | 7.3 | 15.2 | 0.500(5/10) | 0.500(5/10) |
| 1CTJA | 89 | 0.632(12/19) | 9.1 | 13.7 | 0.786(11/14) | 0.889(8/9) |
| 1J75A | 57 | 0.885(23/26) | 7.4 | 12.4 | 0.800(8/10) | 0.875(7/8) |
| 1ECAA | 136 | 0.400(12/30) | 9.5 | 17.1 | 0.263(5/19) | NA(0/0) |
| 1FIOA | 190 | 0.700(21/30) | 9.2 | 17.0 | 0.692(18/26) | 0.778(14/18) |
| 1C75A | 71 | 0.455(5/11) | 10.1 | 14.1 | 0.455(5/11) | 0.600(3/5) |
| 1HCRA | 52 | 0.800(4/5) | 8.8 | 12.4 | 1.000(1/1) | NA(0/0) |
| Average | 0.706 | 8.86 | 14.15 | 0.692 | 0.774 | |
Columns 6 and 7 of Table II denote the performance of our method when contacting residues are separated by at least 12 and 24 residues. The proposed method results in an average accuracy of 0.692 and 0.774, respectively. Similarly, the average coverage for these two cases is 0.276 and 0.146. For some of the test cases (i.e., 1HXIA, 1ELRA, and 1HCRA) there were no predictions for residue separation value of 24. For these cases, accuracy value was not reported.
The topology of these test proteins was also calculated from the predicted contacts. In almost all cases, the correct topology was predicted. For example, in the case of protein 1IG5 anti-parallel contact between helix 1 and 2, 1 and 5, 2 and 3, and, 4 and 5 was predicted by our contact prediction method. 1IG5 also has 5% beta strand residues (2 small β strands). Our method also predicted an anti-parallel sheet formation between β strand 1 and 2 (denoted as S1 and S2 in Figure 4). These anti-parallel contacts are also found in the native structure of protein 1IG5 as shown in Figure 4.
Figure 4.

3D representation of the native structure of protein 1IG5. The proposed method correctly identified the topology of this protein(AP contacts between H1–H2, H1–H5, H2–H3, H4–H5 and S1–S2).
For all the previous results, secondary structure information was derived using DSSP which in turn uses the tertiary structure of the protein. For new proteins, this accurate secondary structure information will not be available and one will have to rely on secondary structure prediction techniques that only use the sequence information. Another test was conducted to estimate the sensitivity of the proposed method with respect to the secondary structure information. PSIPRED (Jones, 1999) uses multi-stage feed forward neural networks for secondary structure prediction by incorporating profile information derived from position specific scoring matrices. It was used to generate the secondary structure information for all the 11 proteins of Test Set 1. Residue contacts were calculated using this new set of secondary structure information and the results are presented in Table III. An average accuracy of 0.637, 0.638 and 0.570 was found for residue separation of 6, 12 and 24. The average true positive and false positive distance was 9.39 Å and 15.51 Å. For most of the cases, the accuracy does not change by much except protein 1E29. Protein 1E29 is a 135 residue protein with 6 α-helices and 2 β-strands. PSIPRED predicts 7 α-helices and 3 β-strands, where the extra helix is predicted between helix 4 and helix 6. The presence of this extra helix causes an incorrect topology prediction, thereby producing a low accuracy value of 0.159. The average accuracy obtained using secondary structure information from PSIPRED is slightly lower than one obtained using DSSP. The consistent accuracy of the proposed method when true secondary structure information is not present further establishes the effectiveness of the proposed method.
Table III.
Residue contact prediction results when tested on 11 α-helical test proteins of test set 1 with secondary structure information derived using PSIPRED (Jones, 1999).
| Residue Separation =6 | Residue Separation =12 | Residue Separation =24 | ||||
|---|---|---|---|---|---|---|
| PDB ID | Length | Accuracy | AvgTPdis | AvgFPdis | Accuracy | Accuracy |
| 1IG5A | 75 | 0.905(19/21) | 9.5 | 12.3 | 0.905(19/21) | 1.000(4/4) |
| 1HXIA | 108 | 0.842(16/19) | 8.8 | 18.6 | 0.857(6/7) | NA (0/0) |
| 1SKNP | 74 | 0.417(5/12) | 10.1 | 14.8 | 0.600(3/5) | NA(0/0) |
| 1ELRA | 128 | 0.941(32/34) | 8.8 | 13.1 | 0.923(12/13) | NA(0/0) |
| 1E29A | 135 | 0.159(7/44) | 10.0 | 23.3 | 0.150(6/40) | 0.154(6/39) |
| 1CTJA | 89 | 0.722(13/18) | 9.3 | 13.8 | 0.769(10/13) | 0.778(7/9) |
| 1J75A | 57 | 0.750(9/12) | 9.4 | 12.6 | 0.500(1/2) | NA(0/0) |
| 1ECAA | 136 | 0.500(14/28) | 9.6 | 16.9 | 0.400(6/15) | NA(0/0) |
| 1FIOA | 190 | 0.477(21/44) | 9.1 | 18.8 | 0.452(19/42) | 0.455(15/33) |
| 1C75A | 71 | 0.467(7/15) | 9.6 | 14.1 | 0.467(7/15) | 0.467(7/15) |
| 1HCRA | 52 | 0.833(5/6) | 9.1 | 12.4 | 1.000(1/1) | NA(0/0) |
| Average | 0.637 | 9.39 | 15.51 | 0.638 | 0.570 | |
Another analysis was carried out to estimate the average distance of true positives and false positives. For a blind experiment, one can not determine whether a predicted contact is a TP or FP until the structure of protein under consideration is determined. A high value of accuracy is desired from any contact prediction method but it is important to estimate and measure the impact of false positive predictions. If a contact prediction method has a high value of accuracy but it produces some (few) false contacts that are far off in the native structure then this method might not produce a good set of restraints (for 3-D protein structure generation). Thus, a good prediction scheme should not only have a high accuracy value but the false positives should not correspond to unrealistic distances in the native structure of the protein either.
For all of the test proteins in test set 1, the average distance of true positives and false positives was calculated from the native structure. These values are reported in columns four and five of Table II. The average true positive and false positive distance is 8.86 and 14.15 Å, respectively for all contacts that were separated by more than 6 residues. This average false positive distance is only 2.15 Å more than our prediction range. If these contacts were to be used to derive restraints for 3D structure prediction in the form of quadratic penalty terms in the objective function then there will not be large violations because of the false positives in the predictions. The average distance between all non-contacting residues, that are 6 residues apart, was calculated for all the 11 proteins of this test set using their actual structures. This distance can be compared with the average false positive distance produced by the proposed method. The average distance for this test set was 20.82 Å which is much higher than 14.15 Å. An average value of 8.86 Å for true positive contacts implies that on an average non-local contacts are separated by about 9 Å. This result is also consistent with our contact definition.
4.2 Protein Test Set 2
The second test set used to compare the performance of our method was taken from Vicatos et al. (2005), where a new method based on correlated mutations analysis (CMA) has been presented. Correlation analysis was performed using a new set of descriptors based on the physiochemical properties of residues. Initially a large set of descriptors was identified but Principal Component Analysis was performed to reduce this to a small set of descriptors that accounted for most of the variations. It was found that the use of new descriptors resulted in more accurate predictions compared to other CMA methods. To define a contact, Vicatos et al. (2005) used a distance cutoff of 6 Å. According to their definition, a contact was said to occur only when the distance between contacting residues was less than 6 Å. Also, only non-local contacts that were separated by 8 or more residues were considered. Prediction results were found to be most accurate for two descriptors, PRIN1 and PRIN3. These components were found to have strong correlation with hydrophobicity and pkN values of amino acids. A set of 127 proteins (from different structural classes) were tested and the main descriptor PRIN1 (which has a strong correlation to hydrophobicity) was found to produce the most reliable results. In this work, we test our contact prediction method on the α-helical proteins of the test set of Vicatos et al. (2005). The remainder of this document will refer to this as test set 2.
The proposed method was only tested on the α-helical proteins of this test set. All proteins with more than 3 β-strands or 10% β residues were not included in this test. This results in a set of 25 α-helical proteins. This set was further divided into two parts. The first part constitutes only single domain proteins. Proteins with more than one domain were included in the second part of Table IV.
Table IV.
Residue contact prediction results when tested on 25 α-helical test proteins of test set 2. (Vicatos et al., 2005)
| Single Domain Proteins | |||||||
|---|---|---|---|---|---|---|---|
| Residue Seperation=6 | ResSep=8 | ResSep=12 | ResSep=24 | ||||
| PDB ID | Length | Accuracy | AvgTPdis | AvgFPdis | Accuracy | Accuracy | Accuracy |
| 1IF1 | 105 | 0.786(22/28) | 7.4 | 12.9 | 0.786(22/28) | 0.786(22/28) | 0.722(13/18) |
| 1FIP | 41 | 0.667(12/18) | 10.4 | 14.0 | 0.647(11/17) | 0.571(8/14) | 0.000(0/2) |
| 1AOY | 71 | 1.000(20/20) | 7.3 | 0.0 | 1.000(15/15) | 1.000(2/2) | NA(0/0) |
| 1ACA | 85 | 0.556(10/18) | 10.2 | 14.7 | 0.556(10/18) | 0.533(8/15) | 0.833(5/6) |
| 1LXL | 99 | 0.658(25/38) | 9.1 | 15.7 | 0.594(19/32) | 0.500(9/18) | 0.000(0/6) |
| 1RSS | 135 | 0.875(49/56) | 7.8 | 16.1 | 0.860(43/50) | 0.806(25/31) | 0.556(5/9) |
| 1BBH | 126 | 0.333(6/18) | 8.3 | 14.9 | 0.333(5/15) | 0.300(3/10) | 0.000(0/3) |
| 1BUN | 119 | 0.434(23/53) | 8.5 | 17.3 | 0.375(18/48) | 0.370(17/46) | 0.359(14/39) |
| 1R1R | 85 | 0.844(27/32) | 7.8 | 13.3 | 0.815(22/27) | 0.792(19/24) | 0.882(15/17) |
| 1BMF | 105 | 0.571(8/14) | 9.2 | 15.3 | 0.500(6/12) | 0.556(5/9) | 0.500(4/8) |
| 1AU1 | 166 | 0.434(23/53) | 9.2 | 16.8 | 0.434(23/53) | 0.423(22/52) | 0.412(14/34) |
| 1FCY | 181 | 0.590(23/39) | 8.7 | 17.3 | 0.515(17/33) | 0.462(12/26) | 0.375(6/16) |
| 1ECM | 85 | 0.556(5/9) | 9.3 | 15.6 | 0.556(5/9) | 0.500(4/8) | NA(0/0) |
| 1A91 | 70 | 0.429(9/21) | 9.2 | 16.2 | 0.429(9/21) | 0.429(9/21) | 0.357(5/14) |
| 1QRV | 67 | 0.750(3/4) | 9.3 | 13.1 | 0.750(3/4) | NA(0/0) | NA(0/0) |
| 1HIW | 115 | 0.762(16/21) | 9.0 | 13.2 | 0.750(15/20) | 0.706(12/17) | NA(0/0) |
| Average | 0.640 | 8.79 | 14.15 | 0.619 | 0.582 | 0.416 | |
| Multi-Domain Proteins | |||||||
| Residue Seperation=6 | ResSep=8 | ResSep=12 | ResSep=24 | ||||
| PDB ID | Length | Accuracy | AvgTPdis | AvgFPdis | Accuracy | Accuracy | Accuracy |
| 2TDX | 71 | 0.778(7/9) | 9.8 | 14.1 | 0.750(6/8) | 0.600(3/5) | NA (0/0) |
| 1ZYM | 125 | 0.625(15/24) | 9.1 | 13.9 | 0.619(13/21) | 0.667(12/18) | 0.667(8/12) |
| 1JI6 | 226 | 0.133(8/60) | 10.3 | 19.6 | 0.091(5/55) | 0.049(2/41) | 0.000(0/11) |
| 1PPR | 146 | 0.290(9/31) | 10.2 | 16.5 | 0.280(7/25) | 0.308(4/13) | 1.000(2/2) |
| 1AQT | 45 | 1.000(1/1) | 5.8 | 0.0 | 1.000(1/1) | NA(0/0) | NA(0/0) |
| 1IVH | 150 | 0.500(19/38) | 9.4 | 16.7 | 0.514(18/35) | 0.516(16/31) | 0.300(3/10) |
| 1A26 | 134 | 0.478(11/23) | 9.3 | 15.8 | 0.500(10/20) | 0.500(9/18) | 0.300(3/10) |
| 1AF7 | 57 | 0.682(15/22) | 9.4 | 14.2 | 0.667(14/21) | 0.500(7/14) | NA(0/0) |
| 1AGR | 114 | 0.500(10/20) | 10.2 | 18.4 | 0.500(10/20) | 0.471(8/17) | 0.467(7/15) |
| Average | 0.554 | 9.28 | 14.36 | 0.547 | 0.451 | 0.289 | |
Table IV presents the test results of our method on test set 2. The contacts that are separated by 6, 12 and 24 residues are reported in this table. An additional column reporting accuracy values for contacts separated by 8 or more residues is also included in this table, as published in Vicatos et al. (2005). For contacts that are separated by 6 or more residues, an average accuracy of 0.640 was obtained for 16 single domain proteins. The highest accuracy was obtained for protein 1AOY where all the predicted contacts were true positives. The average accuracy for multi-domain proteins was 0.554. The tertiary structure of multi-domain proteins is also stabilized by the contacts from other domains of the same protein. These external contacts have not been modeled in the proposed approach and thus a lower value of accuracy is obtained for these proteins (i.e., 1PPR, 1JI6).
The average TP and FP distance was also calculated for this test set. These values are reported in columns four and five of Table IV. An average value of 8.79 Å and 9.28 Å was obtained for true positive contacts for single and multi-domain proteins. This average value is also consistent with the average value obtained for test set 1. The average value of false positive distance for single and multi-domain proteins was 14.15 Å and 14.36 Å, respectively. The average false positive distance for single domain proteins of test set 2 is roughly same as test set 1. The average distance between non-contacting residues, that are at least 6 residues apart, was also calculated for this test set and was found to be 23.05 Å. This distance is also higher than the average false positive distance of 14.15 Å and 14.36 Å. A higher value of average false positive distance was produced for protein 1JI6. This protein has 3 domains with domain 1 containing all the α-helices and domain 2 and 3 containing all the β-strands. The α-helices of domain 1 contact strands from other 2 domains and some of these contacts are responsible for the compact tertiary structure of this protein.
4.3 Protein Test Set 3
The third test set used to measure the effectiveness of the proposed method was taken from the work published by McAllister et al. (2006). This work presents an optimization based framework to generate interhelical distance restraints between hydrophobic residues in α-helical globular proteins. This method was tested on 25 α-helical single domain proteins. The length of these proteins range from 38 to 150 residues and the number of helices varying from 2 to 8. Our method was tested on all of the 25 proteins and testing results are reported in Table V. The average accuracy obtained for contacts that are at least 6, 12, and 24 residue apart was 0.638, 0.618 and 0.641 respectively. This method produced a coverage of 0.27, 0.24 and 0.14 for the three values of residue separation. The average true and false positive distance for this test was 9.18 Å and 13.9 Å respectively. These distances are in the same range as found on the previous two test sets. Similarly, the average distance between all non-contacting residues, that are at least 6 residues apart, was also calculated for all the 25 proteins using their actual structures. The average distance for this est set was 21.23 Å.
Table V.
Residue contact prediction results when tested on 25 α-helical single domain test proteins of test set 3. (McAllister et al., 2006)
| PDB ID | Length | Residue Separation =6 | Residue Separation =12 | Residue Separation =24 | ||
|---|---|---|---|---|---|---|
| Accuracy | AvgTPdis | AvgFPdis | Accuracy | Accuracy | ||
| 1rop | 56 | 1.000(10/10) | 8.9 | 0.0 | 1.000(9/9) | NA(0/0) |
| 1erp | 38 | 0.667(10/15) | 8.9 | 13.5 | 0.636(7/11) | 0.429(3/7) |
| 1mbe | 52 | 0.909(10/11) | 9.6 | 13.7 | 1.000(2/2) | NA(0/0) |
| 1mbh | 52 | 0.778(7/9) | 9.1 | 12.9 | 0.667(2/3) | NA(0/0) |
| 1uxd | 59 | 0.909(10/11) | 7.4 | 14.7 | 1.000(10/10) | 1.000(4/4) |
| 1hta | 68 | 0.625(5/8) | 9.4 | 12.9 | 0.625(5/8) | NA(0/0) |
| 1bha | 67 | 0.222(2/9) | 10.4 | 15.1 | 0.400(2/5) | NA(0/0) |
| 1ail | 70 | 0.455(5/11) | 9.4 | 13.8 | 0.250(2/8) | NA(0/0) |
| 1nre | 81 | 0.667(10/15) | 8.8 | 13.3 | 0.667(10/15) | 1.000(1/1) |
| 2ezh | 65 | 0.846(11/13) | 9.1 | 15.7 | 0.667(4/6) | NA(0/0) |
| 1hsn | 79 | 0.250(2/8) | 10.7 | 18.9 | 0.000(0/6) | 0.000(0/6) |
| 1cc5 | 83 | 0.571(4/7) | 9.0 | 13.6 | 0.571(4/7) | 0.800(4/5) |
| 1p68 | 102 | 0.867(13/15) | 8.9 | 13.9 | 1.000(9/9) | 1.000(7/7) |
| 1r69 | 63 | 1.000(8/8) | 8.4 | 0.0 | 1.000(4/4) | 1.000(4/4) |
| 1b4f | 74 | 0.684(13/19) | 9.8 | 14.7 | 0.615(8/13) | 0.500(2/4) |
| 1g7d | 106 | 0.579(11/19) | 8.9 | 14.2 | 0.583(7/12) | 0.667(6/9) |
| 2mhr | 118 | 0.600(21/35) | 9.4 | 13.9 | 0.615(16/26) | 1.000(3/3) |
| 1a1w | 83 | 0.783(18/23) | 9.0 | 13.4 | 0.786(11/14) | 1.000(6/6) |
| 2tmv | 154 | 0.488(21/43) | 7.2 | 19.0 | 0.512(21/41) | 0.618(21/34) |
| 2ilk | 155 | 0.375(15/40) | 9.2 | 24.0 | 0.276(8/29) | 0.320(8/24) |
| 1gak | 137 | 0.395(17/43) | 9.8 | 16.9 | 0.462(12/26) | 0.250(3/12) |
| 1a17 | 159 | 0.750(27/36) | 8.6 | 14.5 | 0.692(9/13) | 0.800(4/5) |
| 1fc3 | 119 | 0.719(23/32) | 9.7 | 13.2 | 0.739(17/23) | 0.636(7/11) |
| 1ash | 147 | 0.414(12/29) | 9.6 | 15.8 | 0.333(8/24) | 0.286(2/7) |
| 1mba | 146 | 0.400(18/45) | 10.4 | 16.0 | 0.343(12/35) | 0.231(6/26) |
| Average | 0.638 | 9.18 | 13.90 | 0.618 | 0.641 | |
The average false positive distance for protein 2ILK was 24.0 Å. Although this protein is classified as a single domain protein, this has a very peculiar topology where the last two helices are not part of the compact protein structure. These two helices contact each other and are quite far from rest of the protein. Because of this unusual topology, a high value of average false positive distance is produced for this case.
4.4 Protein Test Set 4
The last test set was taken from the recently published work of Wu and Zhang (2008). In this work the authors have compared different machine learning methods (sequence-based and template-based) for residue contact prediction. They tested different contact prediction methods on a test set of 554 non-homologous proteins with a pair-wise sequence identity less than 25%. The length of these proteins varies from 50 to 300 residues. They classified these proteins into “Easy” (220 proteins), “Medium” (98 proteins), “Hard” (220 proteins) and “Very Hard” (16 proteins) targets based on the threading significance score [refer Wu and Zhang (2008) for a complete description of their method].
Test set 4 was created from the ”Hard” and ”Very Hard” proteins of Wu and Zhang (2008) test set. The α-helical and β-strand residue percentage was calculated for each of these cases to identify α-helical proteins. There were 92 proteins (86 “Hard” and 4 “Very Hard” targets) with more than 15% α-helical residues and less than 10% β-strand residues, which we classified as α-helical proteins. Test set 4 includes these 4 very hard targets and 16 randomly selected proteins from the 86 hard category proteins. Our method was tested on these 20 proteins and the results are presented in Table VI. The average accuracy for residue separation of 6 was 0.658 and 0.679 for very hard and hard proteins, respectively. The highest accuracy was obtained for protein 1II0 (84 residues) where the correct topology was predicted with a contact prediction accuracy of 0.914. The average true positive and false positive distance for the hard test proteins was 8.75 Å and 14.01 Å, which is in the same range as found on the previous test sets. An overall value of ~ 14 Å for average false positive distance across all four independent test sets underscores the effectiveness of the proposed method.
Table VI.
Residue contact prediction results when tested on 20 α-helical test proteins of test set 4 [4 proteins of very hard type and 16 proteins of hard type] (Wu and Zhang, 2008).
| “Very Hard” Type | ||||||
|---|---|---|---|---|---|---|
| Residue Seperation=6 | ResSep=12 | ResSep=24 | ||||
| PDB ID | Length | Accuracy | AvgTPdis | AvgFPdis | Accuracy | Accuracy |
| 1UGL | 50 | 0.667(10/15) | 6.6 | 12.5 | 0.692(9/13) | 0.667(6/9) |
| 1HA8 | 51 | 0.867(13/15) | 9.3 | 16.2 | 0.667(4/6) | 0.500(2/4) |
| 1BG8 | 76 | 0.667(10/15) | 9.4 | 14.9 | 0.444(4/9) | NA(0/0) |
| 1VFI | 95 | 0.432(16/37) | 7.8 | 21.8 | 0.400(12/30) | 0.381(8/21) |
| Average | 0.658 | 8.27 | 16.35 | 0.550 | 0.516 | |
| “Hard” Type | ||||||
| Residue Seperation=6 | ResSep=12 | ResSep=24 | ||||
| PDB ID | Length | Accuracy | AvgTPdis | AvgFPdis | Accuracy | Accuracy |
| 1MDY | 62 | 0.667(4/6) | 9.6 | 14.6 | 0.667(4/6) | 0.000(0/1) |
| 1BBY | 69 | 0.667(8/12) | 9.1 | 13.8 | 0.700(7/10) | NA(0/0) |
| 1KJS | 74 | 0.800(12/15) | 8.8 | 9.6 | 0.818(9/11) | 0.714(5/7) |
| 1V54 | 79 | 0.688(11/16) | 7.3 | 13.9 | 0.875(7/8) | 1.000(1/1) |
| 1CF7 | 82 | 0.900(9/10) | 7.3 | 12.1 | 1.000(6/6) | 1.000(4/4) |
| 1IIO | 84 | 0.917(11/12) | 9.2 | 13.8 | 0.917(11/12) | 0.750(3/4) |
| 1E2A | 102 | 0.778(7/9) | 8.4 | 12.9 | 0.778(7/9) | NA(0/0) |
| 1JR8 | 105 | 0.294(10/34) | 10.6 | 17.7 | 0.250(7/28) | 0.000(0/13) |
| 1ZZP | 109 | 0.727(16/22) | 8.6 | 14.2 | 0.750(15/20) | 0.750(3/4) |
| 1OCZ | 109 | 0.833(20/24) | 8.8 | 12.3 | 0.882(15/17) | 1.000(6/6) |
| 1TKN | 110 | 0.808(21/26) | 8.8 | 14.0 | 0.895(17/19) | 1.000(1/1) |
| 1ENW | 114 | 0.500(8/16) | 8.6 | 16.0 | 0.385(5/13) | 0.250(2/8) |
| 1V3F | 120 | 0.735(25/34) | 7.7 | 11.8 | 0.742(23/31) | 0.724(21/29) |
| 1BGF | 124 | 0.389(14/36) | 8.9 | 14.9 | 0.280(7/25) | 0.333(2/6) |
| 1X91 | 149 | 0.769(30/39) | 8.9 | 15.1 | 0.680(17/25) | 1.000(1/1) |
| 1WIX | 164 | 0.396(19/48) | 9.4 | 17.5 | 0.219(7/32) | 0.056(1/18) |
| Average | 0.679 | 8.75 | 14.01 | 0.677 | 0.613 | |
A residue contact map for four proteins from these four test sets is shown in Figure 5. In these plots the upper triangle shows the non-local hydrophobic contacts predicted by our method and the lower triangle shows all contacts (not just hydrophobic) that are present in the native structure of the protein (shown in dark blue color). The contacts in the upper triangle are shown using three different colors. Contacts shown by red color are true positive contacts. False positives are shown by yellow color and missing contacts are shown by light blue color. It is important to further highlight the fact that total number of off-diagonal contacts shown in the upper triangle is less than the number of off-diagonal contacts shown in the lower triangle. This is because only non-local hydrophobic contacts are shown in the upper triangle whereas all types of contacts are shown in the lower triangle.
Figure 5.
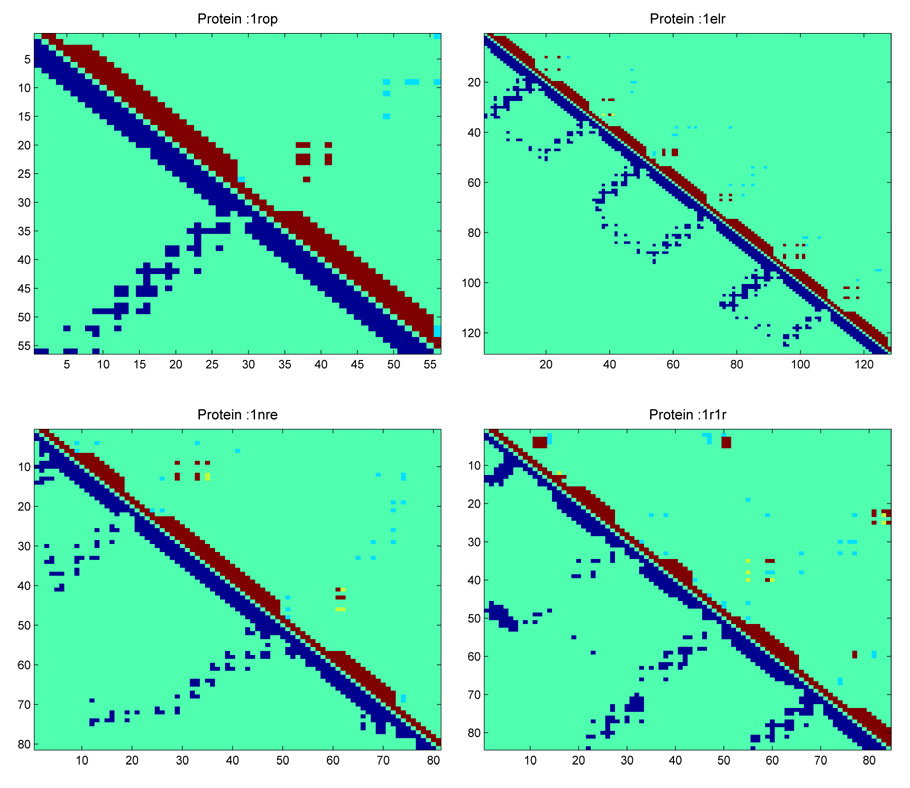
Residue Contact Map of Protein 1ROP, 1ELR, 1NRE and 1R1R. Dark blue color represents contacts (hydrophobic and non-hydrophobic) in the native structure (lower triangle). Red color represents correctly predicted contacts (TP). Yellow color represents incorrectly predicted contacts (FP). Light blue color represents missing contacts.
Protein 1ROP is a 56 residue protein made up of 2 helices [residue location: h1(3–28), h2(32–55)]. The residue contact map for protein 1ROP is shown in the upper left hand side of Figure 5. In the native structure, helix 1 contacts helix 2 in an anti-parallel fashion. The same topology is obtained using the proposed method. For this case there were no false positives (as is evident from the absence of yellow points in the upper triangle of this map). This method was able to correctly identify 10 non-local interhelical contacts for this protein. The native structure also has some non-hydrophobic interhelical contacts between helix 1 and helix 2. These contacts are not predicted by our method and are missing from the upper triangle.
Protein 1ELR is a 128 residue protein made up of 7 helices [residue location: h1(2–16), h2(20–33), h3(38–51), h4(54–70), h5(75–91), h6(95–108), h7(112–127)]. The residue contact map for protein 1ELR is shown in the upper right hand side of Figure 5. In the native structure, each helix contacts the next helix in an anti-parallel fashion. the same topology is obtained using the proposed method. All of these interhelical contacts are shown in red color in the contact map for protein 1ELR. There are two false positives (show by yellow points in the upper triangle of this map). These two false positives correspond to contact between helix 2 and helix 3. The proposed method was able to correctly identify 33 out of 34 non-local interhelical contacts for this protein. The native structure also contains some non-local and non-hydrophobic contacts between loops and helices of this protein. These contacts were set as “no-contact” as part of the preprocessing step of this model and therefore, they are missing in the upper triangular part of the figure. Similar plots have been shown for protein 1NRE (81 res) and 1R1R (85 res) in Figure 5. This figure demonstrates that the presented method can be effectively used to capture critical contacts of a helical protein.
From Table II–Table VI, it can be seen that our method consistently produces an accuracy value of ~ 66% across all test sets. The consistent performance across all test sets further establishes the effectiveness of this method.
5 Conclusion
We have presented a new integer linear optimization based formulation to predict inter-helical hydrophobic residue contacts in α-helical proteins. A binary variable is defined for each residue pair of a protein and a high resolution force field is used as a lookup table to assign a distance dependent energy value for these residue pairs. The formulation then minimizes the sum of contact energies while satisfying a set of constraints. These constraints are based on the commonly observed contact distances between various elements of a secondary structure of a protein. This model also offers the flexibility of incorporating additional constraints where a user can add unique and problem specific constraints to the model. The ability to generate more than one solution highlights the algorithmic advantage of the model. The presented method was tested on four different test sets of α-helical proteins and produced an average accuracy of ~ 66% for single domain proteins. This level of accuracy is higher than other contact prediction methods. It is believed that integration of this approach with other structure generation and structure prediction algorithm can definitely aid in protein structure prediction.
Acknowledgments
CAF gratefully acknowledges financial support from National Science Foundation, National Institutes of Health (R01 GM52032; R24 GM069736) and U.S. Environmental Protection Agency, EPA (GAD R 832721-010). Although the research described in the article has been funded in part by the U.S. Environmental Protection Agency’s STAR program through grant (R 832721-010), it has not been subjected to any EPA review and does not necessarily reflect the views of the Agency, and no official endorsement should be inferred.
Appendix 1: Intrahelical distance distribution

Figure A.I: Distribution of distance occurrences for intrahelical residues at position (i,i+2) within the PDBselect25 dataset.

Figure A.II: Distribution of distance occurrences for intrahelical residues at position (i,i+7) within the PDBselect25 dataset.

Figure A.III: Distribution of distance occurrences for intrahelical residues at position (i,i+8) within the PDBselect25 dataset.
References
- Anfinsen CB. Principles that govern the folding of protein chains. Science. 1973;181(4096):223–230. doi: 10.1126/science.181.4096.223. [DOI] [PubMed] [Google Scholar]
- Berman HM, Westbrook J, Feng Z, Gilliland G, Bhat TN, Weissig H, Shindyalov IN, Bourne PE. The Protein Data Bank. Nucleic Acids Research. 2000;28:235–242. doi: 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonneau R, Ruczinski I, Tsai J, Baker D. Contact Order and ab-initio Protein Structure Prediction. Protein Science. 2002;11:1937–1944. doi: 10.1110/ps.3790102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Hwang J. Prediction of Disulfide Connectivity From Protein Sequences. Proteins: Structure, Function, and Bioinformatics. 2005;61:507–512. doi: 10.1002/prot.20627. [DOI] [PubMed] [Google Scholar]
- Cheng J, Baldi P. A Machine Learning Information Retrieval Approach to Protein Fold Recognition. Bioinformatics. 2006;22:1456–1463. doi: 10.1093/bioinformatics/btl102. [DOI] [PubMed] [Google Scholar]
- Cheng J, Baldi P. Improved Residue Contact Prediction Using Support Vector Machines and a Large Feature Set. BMC Bioinformatics. 2007;8:113–121. doi: 10.1186/1471-2105-8-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng J, Saigo H, Baldi P. Large-scale Prediction of Disulphide Bridges Using Kernel Methods, Two-Dimensional Recursive Neural Networks, and Weighted Graph Matching. Proteins: Structure, Function, and Bioinformatics. 2006;62:617–629. doi: 10.1002/prot.20787. [DOI] [PubMed] [Google Scholar]
- Chuang C, Chen C, Yang J, Lyu P, Hwang J. Relationship Between Protein structures and Disulfide Bonding Patterns. Proteins: Structure, Function, and Bioinformatics. 2003;53:1–5. doi: 10.1002/prot.10492. [DOI] [PubMed] [Google Scholar]
- Fariselli P, Casadio R. A Neural Network Based Predictor of Residue Contacts in Proteins. Protein Engineering. 1999;12:15–21. doi: 10.1093/protein/12.1.15. [DOI] [PubMed] [Google Scholar]
- Fariselli P, Olmea O, Valencia A, Casadio R. Prediction of Contact Maps with Neural Networks and Correlated Mutations. Protein Engineering. 2001a;13:835–843. doi: 10.1093/protein/14.11.835. [DOI] [PubMed] [Google Scholar]
- Fariselli P, Olmea O, Valencia A, Casadio R. Progress in Predicting Inter-Residue Contacts of Proteins With Neural Networks and Correlated Mutations. Proteins: Structure, Function, and Bioinformatics. 2001b;5:157–162. doi: 10.1002/prot.1173. [DOI] [PubMed] [Google Scholar]
- Floudas CA. Computational Methods in Protein Structure Prediction. Biotechnology and Bioengineering. 2007;97(2):207–213. doi: 10.1002/bit.21411. [DOI] [PubMed] [Google Scholar]
- Floudas CA, Fung HK, McAllister SR, Möonnigmann M, Rajgaria R. Advances in protein structure prediction and de novo protein design : A review. Chemical Engineering Science. 2006;61:966–988. [Google Scholar]
- Göobel U, Sander C, Schneider R, Valencia A. Correlated Mutations and Residue Contacts in Proteins. Proteins: Structure, Function, and Bioinformatics. 1994;18:309–317. doi: 10.1002/prot.340180402. [DOI] [PubMed] [Google Scholar]
- Grana O, Baker D, MacCallum R, Meiler J, Punta M, Rost B, Tress M, Valencia A. CASP6: Assessment of Contact Predictions. Proteins: Structure, Function, and Bioinformatics. 2005;61:214–224. doi: 10.1002/prot.20739. [DOI] [PubMed] [Google Scholar]
- Hamilton N, Burrage K, Ragan MA, Huber T. Protein Contact Prediction Using Patterns of Correlation. Proteins: Structure, Function, and Bioinformatics. 2004;56:679–684. doi: 10.1002/prot.20160. [DOI] [PubMed] [Google Scholar]
- Hobohm U, Sander C. Enlarged Representative Set of Protein Structures. Protein Science. 1994;3:522–524. doi: 10.1002/pro.5560030317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horner DS, Pirovano W, Pesole G. Correlated Substitution Analysis and The Prediction of Amino Acid Structural Contacts. Briefings in Bioinformatics. 2008;9:46–56. doi: 10.1093/bib/bbm052. [DOI] [PubMed] [Google Scholar]
- Jones DT. Protein Secondary Structure Prediction Based on Position-Specific Scoring Matrices. Journal of Molecular Biology. 1999;292:195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- Kabsch W, Sander C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-bonded and Geometrical Features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- Klepeis JL, Floudas CA. ASTRO-FOLD: A Combinatorial and Global Optimization Framework for Ab Initio Prediction of Three-Dimensional Structures of Proteins from the Amino Acid Sequence. Biophysical Journal. 2003c;85:2119–2146. doi: 10.1016/s0006-3495(03)74640-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kundrotas P, Alexov EG. Predicting Residue Contacts Using Pragmatic Correlated Mutations Method: Reducing the False Positives. Bioinformatics. 2006;7:503–512. doi: 10.1186/1471-2105-7-503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lund O, Frimand K, Gorodkin J, Bohr H, Bohr J, Hansen J, Brunak S. Protein Distance Constraints Predicted by Neural Networks and Probability Density Functions. Protein Engineering. 1997;10:1241–1248. doi: 10.1093/protein/10.11.1241. [DOI] [PubMed] [Google Scholar]
- MacCallum R. Striped Sheets and Protein Contact Prediction. Bioinformatics. 2004;20:i224–i231. doi: 10.1093/bioinformatics/bth913. [DOI] [PubMed] [Google Scholar]
- McAllister SR, Floudas CA. Alpha Helical Topology and Tertiary Structure Prediction in Globular Proteins; Proceedings of 46th IEEE Conference on Decision and Control; 2007. pp. 4551–4556. [Google Scholar]
- McAllister SR, Mickus BE, Klepeis JL, Floudas CA. A Novel Approach for Alpha-Helical Topology Prediction in Globular Proteins: Generation of Interhelical Restraints. Proteins: Structure, Function, and Bioinformatics. 2006;65:930–952. doi: 10.1002/prot.21095. [DOI] [PubMed] [Google Scholar]
- Murzin AG, Brenner SE, Hubbard T, Chothia C. SCOP: A Structural Classification of Proteins Database for the Investigation of Sequences and Structures. Journal of Molecular Biology. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- Olmea O, Rost B, Valencia A. Effective Use of Sequence Correlation and Conservation in Fold Recognition. Journal of Molecular Biology. 1999;295:1221–1239. doi: 10.1006/jmbi.1999.3208. [DOI] [PubMed] [Google Scholar]
- Ortiz AR, Kolinski A, Skolnick J. Nativelike Topology Assembly of Small Proteins Using Predicted Restraints in Monte Carlo Folding Simulations. Proceedings of the National Academy of Sciences of the United States of America. 1998a;95:1020–1025. doi: 10.1073/pnas.95.3.1020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortiz AR, Kolinski A, Skolnick J. Fold Assembly of Small Proteins Using Monte Carlo Simulations Driven by Restraints Derived from Multiple Sequence Alighments. Journal of Molecular Biology. 1998b;277:419–448. doi: 10.1006/jmbi.1997.1595. [DOI] [PubMed] [Google Scholar]
- Ortiz AR, Kolinski A, Skolnick J. Tertiary Structure Prediction of the KIX Domain of CBP Using Monte Carlo Simulations Driven by Restraints Derived from Multiple Sequence Alignments. Proteins: Structure, Function, and Bioinformatics. 1998c;30:287–294. doi: 10.1002/(sici)1097-0134(19980215)30:3<287::aid-prot8>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- Punta M, Rost B. PROFcon: Novel Prediction of Long-range Contacts. Bioinformatics. 2005;21:2960–2968. doi: 10.1093/bioinformatics/bti454. [DOI] [PubMed] [Google Scholar]
- Rajgaria R, McAllister SR, Floudas CA. A Novel High Resolution Cα-Cα Distance Dependent Force Field Based on a High Quality Decoy Set. Proteins: Structure, Function, and Bioinformatics. 2006;65:726–741. doi: 10.1002/prot.21149. [DOI] [PubMed] [Google Scholar]
- Rubinstein R, Fiser A. Predicting Disulfide Bond Connectivity in Proteins by Correlated Mutations Analysis. Bioinformatics. 2008;24:498–504. doi: 10.1093/bioinformatics/btm637. [DOI] [PubMed] [Google Scholar]
- Shackelford G, Karplus K. Contact Prediction Using Mutual Information and Neural Nets. Proteins: Structure, Function, and Bioinformatics. 2007;69:159–164. doi: 10.1002/prot.21791. [DOI] [PubMed] [Google Scholar]
- Shao Y, Bystroff C. Predicting Interresidue Contacts Using Templates and Pathways. Proteins: Structure, Function, and Bioinformatics. 2003;53:497–502. doi: 10.1002/prot.10539. [DOI] [PubMed] [Google Scholar]
- Singer MS, Vriend G, Bywater RP. Prediction of Protein Residue Contacts with a PDB-derived Likelihood Matrix. Protein Engineering. 2002;15:721–725. doi: 10.1093/protein/15.9.721. [DOI] [PubMed] [Google Scholar]
- Vicatos S, Kaznessis YN. Separating True Positive Predicted Residue Contacts from False Positive Ones in Mainly α Proteins, Using Constrained Metropolis MC Simulations. Proteins: Structure, Function, and Bioinformatics. 2008;70:539–552. doi: 10.1002/prot.21553. [DOI] [PubMed] [Google Scholar]
- Vicatos S, Reddy BVB, Kaznessis Y. Prediction of Distant Residue Contacts With the Use of Evolutionary Information. Proteins: Structure, Function, and Bioinformatics. 2005;58:935–949. doi: 10.1002/prot.20370. [DOI] [PubMed] [Google Scholar]
- Vullo A, Walsh I, Pollastri G. A Two-stage Approach for Improved Prediction of Residue Contact Maps. Bioinformatics. 2006;7:180–192. doi: 10.1186/1471-2105-7-180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G, Dunbrack RL., Jr PISCES: a protein sequence culling server. Bioinformatics. 2003;19:1589–1591. doi: 10.1093/bioinformatics/btg224. [DOI] [PubMed] [Google Scholar]
- Wu S, Zhang Y. A Comprehensive Assessment of Sequence-based and Template-based Methods for Protein Contact Prediction. Bioinformatics. 2008;24:924–931. doi: 10.1093/bioinformatics/btn069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang GZ, Huang DS. Prediction of Inter-Residue Contacts Map Based on Genetic Algorithm Optimized Radial Basis Function Neural Network and Binary Input Encoding Scheme. Journal of Computer-Aided Molecular Design. 2004;18:797–810. doi: 10.1007/s10822-005-0578-7. [DOI] [PubMed] [Google Scholar]
- Zhao Y, Karypis G. Prediction of Contact Maps Using Support Vector Machines; Proc of the IEEE Symposium on Bioinformatics and Bioengineering; 2003. pp. 26–33. [Google Scholar]


