Measuring and Modeling the Interaction Among Reward Size, Delay to Reward, and Satiation Level on Motivation in Monkeys

Abstract

Motivation is usually inferred from the likelihood or the intensity with which behavior is carried out. It is sensitive to external factors (e.g., the identity, amount, and timing of a rewarding outcome) and internal factors (e.g., hunger or thirst). We trained macaque monkeys to perform a nonchoice instrumental task (a sequential red-green color discrimination) while manipulating two external factors: reward size and delay-to-reward. We also inferred the state of one internal factor, level of satiation, by monitoring the accumulated reward. A visual cue indicated the forthcoming reward size and delay-to-reward in each trial. The fraction of trials completed correctly by the monkeys increased linearly with reward size and was hyperbolically discounted by delay-to-reward duration, relations that are similar to those found in free operant and choice tasks. The fraction of correct trials also decreased progressively as a function of the satiation level. Similar (albeit noiser) relations were obtained for reaction times. The combined effect of reward size, delay-to-reward, and satiation level on the proportion of correct trials is well described as a multiplication of the effects of the single factors when each factor is examined alone. These results provide a quantitative account of the interaction of external and internal factors on instrumental behavior, and allow us to extend the concept of subjective value of a rewarding outcome, usually confined to external factors, to account also for slow changes in the internal drive of the subject.

INTRODUCTION

The motivation to engage in behavior arises from both incentive (or external) factors (e.g., the identity, amount and timing of a rewarding outcome) and drive (or internal factors, e.g., level of hunger or thirst) (Hull 1952; Schultz 1998; Spence 1956; Toates 1986). When external factors are manipulated, monkeys perform instrumental actions more slowly and less accurately when they expect a smaller reward than when they expect a larger reward (Cromwell and Schultz 2003; Hollerman et al. 1998; Matsumoto et al. 2003; Minamimoto et al. 2005; Roesch and Olson 2004). Reaction times are faster when monkeys expect reward delivery to occur immediately after the action than when they expect the reward to be delayed (Roesch and Olson 2005; Tsujimoto and Sawaguchi 2007). In general, the more valuable reward is available, the more strongly a subject is motivated to get it. However, many behavioral studies have shown that the process of valuating a rewarding outcome is subjective (see Mazur 2001, 2005 for a review); that is, choice behavior is often biased toward the subjective value of a reward as opposed to something else (e.g., its size). This tendency is apparent when the choice options differ in more than one dimension, for example, in the choice between a smaller reward available sooner and a larger reward available later (Green et al. 2007; Kable and Glimcher 2007; Kim et al. 2008; Mazur 1984; Mischel et al. 1969). Mainly because of the experimental paradigms used to study choice behavior, the notion of subjective value is typically restricted to the comparison of external factors, like the size or the delay of the reward. More generally, however, the value of an outcome is also influenced by the internal state of the animal, i.e., its drive. For example, monkeys’ preferences change after being fed a preferred food, suggesting that the food's value is discounted or reduced by satiation, a procedure typically know as “devaluation” (Chudasama et al. 2008; Critchley and Rolls 1996; Machado and Bachevalier 2007a,b). However, the relationship between the level of satiation and the value of rewarding options, and more generally the simultaneous impact of both external and internal factors on the value of an outcome, have not yet been systematically examined. Here, we refer to outcome value as motivational value (La Camera and Richmond 2008) to emphasize its control by both external and internal factors and measure motivational value in monkeys performing an instrumental task designed for this.

A measurement of motivational value with standard behavioral procedures like free operant and choice tasks poses a number of potential problems. In typical free operant tasks (Killeen and Hall 2001; Skinner 1966), where the incentive to act is measured by the response rate of the subject performing repeatedly a simple action, motivational value could be inferred by such response rate. However, it is difficult in these tasks to assess the incentive effect of rapidly changing external factors, e.g., those factors changing on a trial-by-trial basis. In choice tasks (Mazur 2001, 2005), despite being reasonable to assume that an animal will work harder for a preferred option, there is no clear means of combining the subjective values for each of the choices into a measure reflecting the overall likelihood to act, i.e., the motivational value. Also, it is not clear how to convert the choice behavior into how hard or accurately will the animal work for the preferred option, were this option to be offered in isolation in exchange for some instrumental effort.

To estimate the motivational value of instrumental actions in monkeys, we used a nonchoice paradigm in which the operant action is the same in all trials, and different trial types are defined by associating different rewarding properties (here reward size and delay-to-reward) with different visual stimuli, or cues. The presence of visual cues allows the monkeys to predict the current rewarding property, so that their behavioral reaction could be modulated quickly on a trial-by-trial basis, like in a choice task, while the internal state of the animal changes slowly as a function of a gradual shift from thirst to satiation (measured by the accumulated reward level). Because the operant demands are constant and there is no choice among actions, the fraction of correctly completed trials, and the reaction times in those trials, can be taken as direct correlates of the motivational value the animal assigns to each trial in the face of its internal drive state. Thus our approach provides a straightforward means to estimate the motivational value of an instrumental action when external factors (here reward size and delay) are manipulated and an internal factor (accumulated reward) is monitored.

We found that the fraction of correctly completed trials was inversely related to delay-to-reward (hyperbolic discounting of reward value) and directly increased by reward size. However, it was also dependent on the accumulated reward, and thus varied, for the same predicted incentive condition, depending on the internal state of the animal. Here, this dependence was modeled as a sigmoidal function of accumulated reward. Finally, the effect of all factors together can be modeled simply through multiplication of the effects of the single factors when these are present alone.

METHODS

Subjects

Eight adult (5–11 kg) rhesus monkeys were used in this study. All the experimental procedures were carried out in accordance with the National Institutes of Health Guide for the Care and Use of Laboratory Animals and were approved by the Animal Care and Use Committee of the National Institute of Mental Health.

Behavioral tasks

Each monkey sat in a primate chair inside a sound-attenuated dark room. Visual stimuli were presented on a computer video monitor in front of the animal. The behavioral paradigms used in these experiments (Fig. 1A) were derived from the multitrial reward schedule task (Bowman et al. 1996). In each trial, 100 ms after the monkey initiated the trial by touching the bar in the chair, a visual cue (13° on a side), which will be described below, was present at the center of the monitor. After 500 ms, a red dot (WAIT, 0.5° on a side) appeared at the center of the monitor. After a time selected randomly from 500, 750, 1,000, 1,250, or 1,500 ms, the signal turned green (GO signal), indicating that the monkey could release the bar to earn a liquid reward. If the monkey responded between 200 ms and 1 s, the signal turned blue (OK signal), signaling the monkey that the trial had been completed correctly. An intertrial interval (ITI) of 1 s was enforced before allowing the next trial to begin.

FIG. 1.

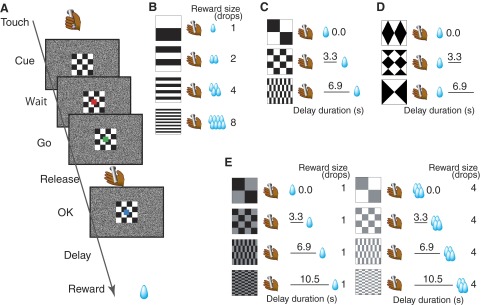
Behavioral task and cue-outcome contingencies. A: sequence of events in the visually triggered bar-release task with incentive cue. The monkey initiates each trial by touching a lever. The monkey is required to respond by releasing the lever when the color of a visual target changed from red to green. A trial is scored as correct if the monkey releases the lever 200-1,000 ms after the target changes to green (Go). If the trial is correctly performed, a blue spot replaces the green target. Water reward is delivered after a delay period. A visual cue presented at the beginning of the trial indicates the duration of the delay or the reward size. B–E: relationship between cue and outcome (size and timing of the reward). B: the 4 cues used in the reward-size task. C: the 3 cues used in the reward-delay task. D: the 3 cues used in the next-trial-delay task. E: the 8 cues used in the reward-size-and-delay task.

If the monkey made an error by releasing the bar before the GO signal or within 200 ms after the GO signal appeared or failed to respond within 1 s after the GO signal, all visual stimuli disappeared, the trial was terminated immediately, and, after the 1-s ITI, the trial was repeated.

Two types of cueing conditions were used. In both conditions, each new trial type was picked at random with equal probability. In the valid cue condition, each cue was associated to a unique contingency, i.e., the delay duration between bar release and reward delivery, the amount of reward that would be delivered (reward size), or both, depending on the task. In the random cue condition, the cues were picked at random from the same set of the cues used for the valid cue condition, regardless of trial type. Thus random cues did not have any predictive value of the forthcoming contingency. There were four task versions: the reward-size task, the reward-delay task, the next-trial-delay task, and the reward-size-and-delay task. In the reward-size task, a reward of one, two, four, or eight drops of water (1 drop = ∼0.1 ml), was delivered immediately (0.2–0.4 s) after a correct bar release. Each reward size was selected randomly with equal probability, i.e., it occurred equally often. In the valid cue condition, each visual cue was associated with only one reward size (Fig. 1B). In the reward-delay task, the water reward (∼0.5 ml) was delivered immediately (0.3 ± 0.1 s) or with an additional delay of either 3.3 ± 0.6 or 6.9 ± 1.2 s after a correct bar release. Each delay duration was chosen randomly with equal probability, just as in the reward-size task. In the valid cue condition, each delay duration was univocally associated to a visual cue (Fig. 1C). In the next-trial-delay task, the water reward (∼0.5 ml) was always delivered immediately (0.3 ± 0.1 s) after a correct bar release, followed by a time out (0, 3.3 ± 0.6, or 6.9 ± 1.2 s) in addition to the ITI (1 s). The visual cue indicated the duration of the time out (Fig. 1D). In the reward-size-and-delay task, either one (∼0.25 ml) or four drops of the water reward was delivered immediately (0.3 ± 0.1 s) or with an additional delay of 3.3 ± 0.6, 6.9 ± 1.2, or 10.5 ± 1.8 s after a correct bar release. The visual cue presented at the beginning of the trial indicated the combination of the forthcoming reward size and delay-to-reward duration (Fig. 1E). Each combination of reward size and delay-to-reward was chosen with equal probability, i.e., occurred equally often. A different set of cues was used for each task (Fig. 1, B–E).

Training and testing procedure

Before the experiment, the monkeys had had experience in performing the cued multitrial reward schedule task (Bowman et al. 1996), which has the same stimulus-response requirements, for >1 mo. We tested the monkeys with the tasks described in the previous subsection. Only one task and one cueing condition were used each day. All eight monkeys were tested first in the reward-delay task with valid cues. The monkeys were tested in the other tasks described in the previous subsection, typically in the following order: the reward-delay task with random cues (6 monkeys); the reward-size-and-delay task (valid cue condition; 4 monkeys); the next-trial-delay task (valid cue condition; 4 monkeys); and the reward-size task (valid and random cue conditions; 3 monkeys). These tasks were introduced as control tasks in a second phase of the study, when not all monkeys were available any longer (which explains the different number of monkeys tested in each task).

Every time a new task was introduced, the monkeys took at most 2 days (typically 1 day) to become familiar with it. We collected behavioral data in the same task for 10–20 daily testing sessions. Each session ended when the monkeys stopped working spontaneously, i.e., when they would not initiate a new trial, presumably because they were sated. On the 5 testing days each week, the monkey earned its daily water in the testing session. Each monkey's performance in these tasks was stable across sessions in terms of the number of correct trials (and thus the total amount of reward received), except for a very few sessions, where the number of correct trials was <80% the average across sessions. These constituted at most two sessions for each subject and were not included in the analysis to have as uniform as possible a dataset with regard to the initial motivational level in each daily session. The data looked only slightly different if those sessions were included (data not shown).

Data analysis and model fitting

All data and statistical analyses were performed using the “R” statistical computing environment (R Development Core Team 2004). The error rate and average reaction time for each incentive condition were calculated for each daily session and averaged across sessions. For each daily session, the error rates in each trial type were defined as the number of error trials divided by the total number of trials of that given type. A trial was considered an error trial if the monkey released the bar either before or within 200 ms after the appearance of the GO signal (early bar release) or failed to respond within 1 s after the GO signal (late bar release). In each correct trial, the reaction time was defined as the time elapsed between the appearance of the GO signal and the bar release. Thus reaction times were restricted to a range of 200-1,000ms. Error trials caused by bar releases occurring in the 100 ms between the beginning of each trial and the appearance of the visual cue were not included in the calculation of the error rates. The results presented in this article concern the totality of error trials, regardless of error type (early vs. late), for the following reasons: 1) although the proportion of early and late errors was different across monkeys, the same patterns were obtained when only early or only late error trials were considered (Supplemental Fig. S1)1 ; 2) the effect of the incentive condition on the early occurrence of bar releases was consistent throughout the time from the beginning to the end of each trial [Supplemental Fig. S2A for comparison, a few distributions of bar release times in correct trials (Bowman et al. 1996) are shown in Supplemental Fig. S2B].

We used repeated-measures ANOVA to test the effect of delay duration on error rate in the reward-delay task and the next-trial-delay task. We also used two-way repeated-measures ANOVA to test the effect of incentive conditions and accumulated reward on average reaction times. We used the general-purpose optimization function “optim” in “R” for fitting the models to the data by sum-of-squares minimization without weighting. The coefficient of determination (r²) was reported as a measure of goodness of fit. We fitted the average data obtained in the reward-size task with a model, 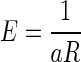, where R is the reward size, a is a constant parameter, and E is the error rate (%) of the monkeys in trials with reward size R (this is Eq. 1 in results). For the data obtained in the reward-size-and-delay task, we used two types of discounting models, the hyperbolic, 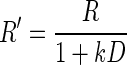(Green and Myerson 2004; Mazur 1984, 2001), and exponential, 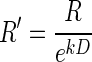(Kagel et al. 1986; Samuelson 1937; Schweighofer et al. 2006) discounting models, where R′ is the discounted value of reward, R is the reward size, k is a temporal discount factor, and D is the delay-to-reward. Replacing reward size, R, with its discounted value R′ into 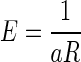linking error rate and reward size in the reward-size task, we obtaine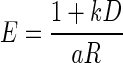d and 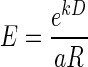as models of hyperbolic and exponential discounting, respectively (these are Eqs. 2 and 3 in results). We fitted these two discounting models to the data with the least square minimization procedure described earlier and compared the models using cross-validation (Shao 1993; Stone 1974), as described next. A single point was removed from each dataset (containing N points) and the theoretical model was fitted to the remaining N − 1 data points using least-squares minimization. The difference between the datum that had been left out and its theoretical prediction by the model (the residual) was calculated. This procedure was repeated for all data points (N times) and repeated on all N(N − 1)/2 datasets obtained by removing a different pair of points each time to increase the number of residuals. The two distributions of N + N(N − 1)/2 residuals, one for each model, were compared using a two-sample Wilcoxon test. The model with a significant smaller median of residuals was considered the better model. The significance level was very high in all cases (P < 0.001). The better model also had the larger relative likelihood of being the correct model as determined by the Akaike Information Criterion (AIC; see results).

The discounting effect of satiation level, f(S), on the reward value as the monkeys proceeded from thirst to satiation during each session was modeled with a sigmoid function of the normalized accumulated reward S, 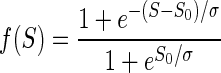, where S₀ is the inflection point of the sigmoid and σ quantifies the width of the sigmoid around S₀. This function is a natural choice for quantities that increase exponentially before undergoing a saturating phase. The normalized accumulated reward was defined as the ratio between the amount of total reward delivered up to time t, R_cum(t) and the total amount of reward R_{cum max} delivered in the entire session: 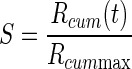. For each monkey, we considered the data collected in the reward-size task and the reward-size-and-delay task. The data from each session were divided into consecutive sextiles (for the reward-size task) or quartiles (reward-size-and-delay task) with respect to the value of S; the error rates were evaluated in each sextile (or quartile), and the results were averaged across sessions for each sextile (or quartile). The models (Eqs. 1–3 in results) were all modified by replacing the reward size R with its satiation-discounted value, R × f(S), producing Eqs. 6 and 7 (see results). For the data collected in the random-cue condition, average reward size across incentive conditions (0.375 ml) was used as the reward size R for fitting. These models were fitted to the average error rate in each sextile (or quartile) using the same least-squares minimization procedure described earlier. Because the error rate curve did not change appreciably in the 0 < S < 1 range for S₀ > 1.5, this value was used as an upper bound during the fitting procedure. An analogous analysis was performed on average reaction times in each sextile (or quartile).

For comparison, an analogous procedure using either normalized time or normalized trial number in place of accumulated reward S was also performed. Normalized time was defined as the time elapsed from the beginning of the session divided by the total duration of the session. Similarly, normalized trial number was defined as the number of trials since the beginning of the session divided by the total number of trials. The error rates were collected in each sextile and averaged across sessions for each sextile. The same discounting function as for f(S) was used in the models (Eqs. 6 and 7 in results) to fit the data, with either normalized time or normalized trial number in place of S.

RESULTS

To study how external and internal factors interact to influence motivation, we had monkeys perform an instrumental task in which we could manipulate external factors, here reward size and delay, independently on a trial-by-trial basis, and monitor the effect of an internal factor, satiation level, that we expected to change slowly through the course of each testing session. For the operant response, the monkeys learned to release a bar when a red spot turned green (Fig. 1A and methods). A bar release before the green spot appeared or after it disappeared was counted as an error. The monkeys had to repeat error trials until executed correctly. A visual cue that appeared at the beginning of each trial indicated the reward contingency, with different cues for each combination of reward size and delay-to-reward (valid cue condition; Fig. 1). In the random cue condition, the same cues were presented but bore no relationship to the forthcoming reward contingency (see methods). When the cues were valid, monkeys reacted to the different cues with different error rates, depending on the predicted reward contingencies and on accumulated reward.

Relationship between expected reward size and motivation

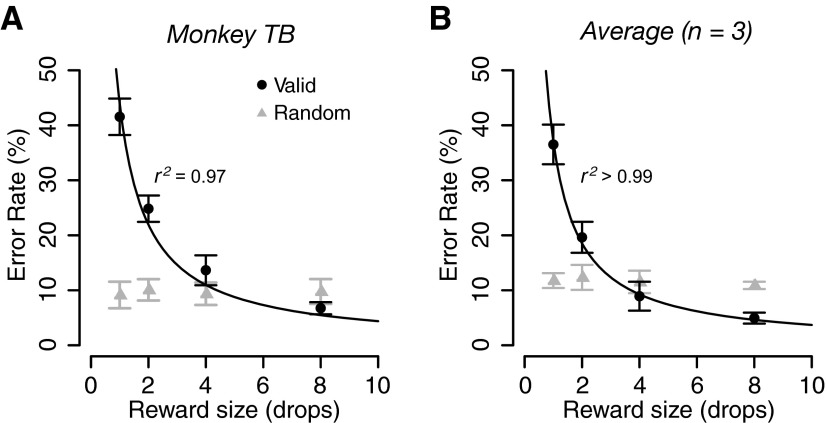
Three monkeys were tested in the reward-size task of Fig. 1B. When the cue indicated the forthcoming reward size (valid cue condition), the error rates progressively decreased as the expected reward size increased for all three subjects and for the average across them (Fig. 2, black circles). The error rates, E, were well approximated by an inverse function of reward size, R

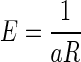(1)

with a constant for all individual subjects and average across monkeys (Fig. 2, black curves; r² (coefficient of determination) > 0.96). The best-fit parameters are reported in Supplemental Table S1.

FIG. 2.

Effect of expected reward size on error rate. Percentage of error trials (mean ± SE) as a function of reward size in (A) monkey TB and (B) in the average across 3 monkeys in the reward-size task. Black circles and gray triangles indicate valid (predictable) and random (unpredictable) conditions, respectively. The black curve is the best fit of Eq. 1 to the data collected in the valid cue condition.

When the cue was selected irrespective of reward size (random cue condition), the error rates were indistinguishable across trial types for any individual monkey (repeated-measures ANOVA across sessions: P > 0.05; Fig. 2A, gray triangles) or in the average across monkeys (F_(3,11) = 0.7, P = 0.6; Fig. 2B, gray triangles).

Effect of predicted delay-to-reward on motivation

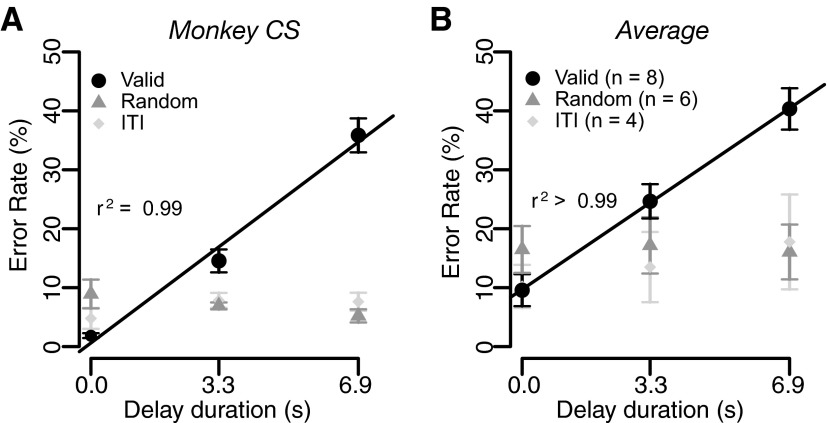
We examined the effect of the predicted duration of the delay-to-reward on motivation by using the reward task with fixed reward size (Fig. 1C). When cues indicated how long the reward would be delayed after a correct bar release (valid cue condition), the error rate increased linearly as predicted delay-to-reward increased in all eight individual monkeys and in the average across monkeys (repeated-measures ANOVA, P < 10⁻⁴; Fig. 3, black circles). In the random cue condition, when the cues did not convey any information about the delay duration, error rates were indistinguishable across the trial types (repeated-measures ANOVA, P > 0.05; Fig. 3, gray triangles).

FIG. 3.

Effect of predicted delay-to-reward on error rate. Percentage of error trials (mean ± SE) as a function of delay duration in (A) monkey CS and (B) in the average across monkeys in the reward-delay task. Black circles, gray triangles, and light gray diamonds indicate valid cue condition, random cue condition, and the next-trial delay task, respectively. The black lines are the regression lines [E = k × delay + constant; (A) k = 4.9 and (B) 4.5 (ranging from 1.8 to 6.6 in 8 monkeys); the r² values are reported in the plots.] Number in parentheses represents the number of subjects.

These results show that there is a temporal discount of reward value caused by the predicted delay-to-reward. In this task, the delayed delivery of reward causes a delay in the beginning of the next trial and thus a delay of the future rewards. Therefore the observed effect of delay-to-reward could be partly caused by the prediction that future rewards after the current trial would be delayed. To examine this possibility, we tested four monkeys in the next-trial-delay task, in which reward was delivered immediately after every successful trial, followed by a delay to the next trial (Fig. 1D). For three of four monkeys and for the average across all four monkeys, the error rates showed no sensitivity to delay of the next trial (repeated-measures ANOVA, P > 0.05; Fig. 3, light gray diamonds). The fourth monkey showed increasing error rates as a function of predicted delay duration to the next trial. Thus in general, temporal discounting is more consistently explained by predicted delay-to-reward than by predicted delay-to-next trial.

Joint effect of predicted reward size and delay-to-reward on motivation

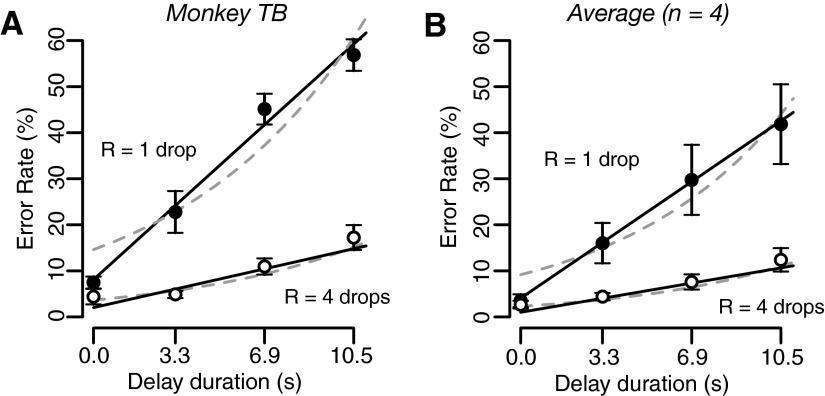
When each combination of reward size and delay duration was indicated by a unique single cue (Fig. 1E), both reward size and delay duration affected error rates. Error rates were lower when the monkeys expected larger reward. For each reward size, there was a linear relationship between error rate and delay duration (Fig. 4 and Supplemental Fig. S3).

FIG. 4.

Effect of predicted reward size and delay-to-reward on error rate. Percentage of error trials (mean ± SE) as a function of delay duration in (A) monkey TB and (B) in the average across 4 monkeys in the reward-size-and-delay task. Filled and open circles correspond to 1 and 4 drops of reward, respectively. Full black lines and dashed gray curves are the best fit of Eqs. 2 and 3, respectively.

We examined whether the data would be well described by a model combining the reward size (Eq. 1) and temporal discounting effects. For this purpose, we tried two functional forms of temporal discounting (see methods): the hyperbolic model (Green and Myerson 2004; Mazur 1984, 2001)

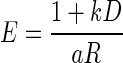(2)

and the exponential model (Kagel et al. 1986; Samuelson 1937; Schweighofer et al. 2006)

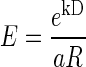(3)

where R is the reward size, D is the delay-to-reward duration, k is the temporal discounting factor, and a is a constant. Both models fit the data well (Fig. 4, black lines and gray curves for Eqs. 2 and 3, respectively; see Supplemental Table S2 for the best-fit parameters). We used cross-validation to compare the goodness of fit for the two models (see methods). In three of four monkeys, the model in Eq. 2 gave a significantly better fit to the data (P < 0.0001, 2-sample Wilcoxon test; Fig. 4A); for the fourth monkey, the model in Eq. 3 was significantly better (P < 0.001; Supplemental Fig. S3D). Equation 2 also provides a better fit to the average data across monkeys (P < 10⁻⁹; Fig. 4B). Note that Eq. 2 predicts that the slopes of the black straight lines (Fig. 4) corresponding to different reward sizes must equal the ratio of the reward sizes, independently of the delay durations used for each reward size. Figure 4 and Supplemental Fig. S3 shows that this prediction is well respected by the fit of model Eq. 2 to the whole data set, making a strong case for this model description of the data. The better model as determined by cross-validation also had the larger relative likelihood of being the correct model as determined by the AIC (see methods and Supplemental Table S2).

Effects of predicted reward size, delay-to-reward, and satiation level on motivation

The effect of one drop of reward on motivation should differ when physiological drive state changes from thirst to satiation. In every daily session, the monkeys were allowed to work until they stopped by themselves, so that the data were collected as the monkeys approached satiation. We defined the normalized accumulated reward, S, which ranged from 0 (beginning of every session) to 1 (at the end of the session), as

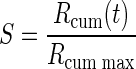(4)

where R_cum is the cumulative reward at time t, and R_{cum max} is the total amount of reward obtained in the session. We divided each session's data of the validly cued reward-size task into consecutive sextiles and analyzed the error rates in each sextile (see methods). For the first sextile (when the monkeys were assumed thirsty), the monkeys performed almost without errors in all reward conditions (Fig. 5). The error rates for each of the three monkeys became progressively larger in succeeding sextiles, i.e., as reward accumulated. The growth is exponential at first, and then it typically saturates (being bounded by the upper value of 100%). Thus we hypothesized the reward value (R′) to be discounted as a sigmoid function f(S) of accumulated reward

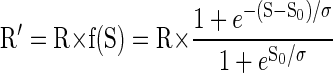(5)

where R is the reward size, and S₀ and σ are constants (the inflection point and the width of the sigmoid function, respectively). As a consequence, Eq. 1 becomes

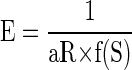(6)

where E is error rate, R is reward size, and a is a constant. The error rates were well explained by Eq. 6 for all three individual subjects (r² > 0.94; Fig. 5, A–C; Supplemental Table S3) and for the average across monkeys (Fig. 5D; r² = 0.98). Note that saturation of the error rates occurs before satiation (S = 1) when S₀ < 1 and does not occur if S₀ > 1. For S₀ > 1.5, the error rate curve did not change appreciably in the 0 < S < 1 range; hence this value was used as an upper bound during the fitting procedure (see methods). The data were also well explained by Eq. 6 when S was replaced with normalized time or number of trials (r² > 0.87, see methods and Supplemental Fig. S4). The same effect of accumulated reward on error rate was found in the random cue condition, where the error rates were well explained by Eq. 6 with R constant (r² >0.74; Supplemental Fig. S5; see also methods).

FIG. 5.

Effect of normalized accumulated reward on error rate. Percentages of error trials (mean ± SE) for each reward size as a function of normalized accumulated reward in the reward-size task are shown for (A–C) 3 monkeys and (D) for the average across the monkeys. The superimposed curves are the best fit of Eq. 6 to the data in each reward size condition.

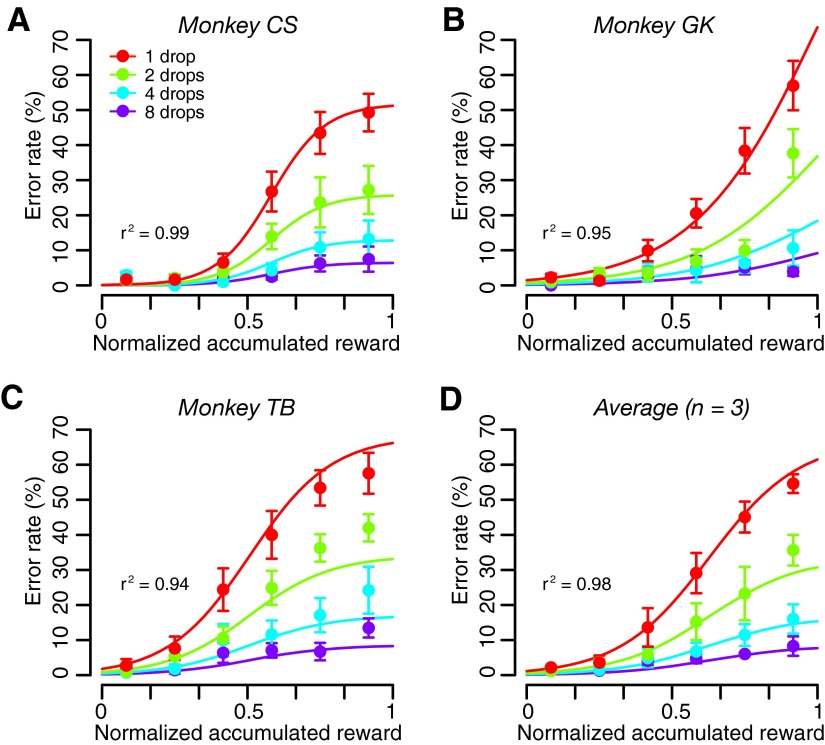
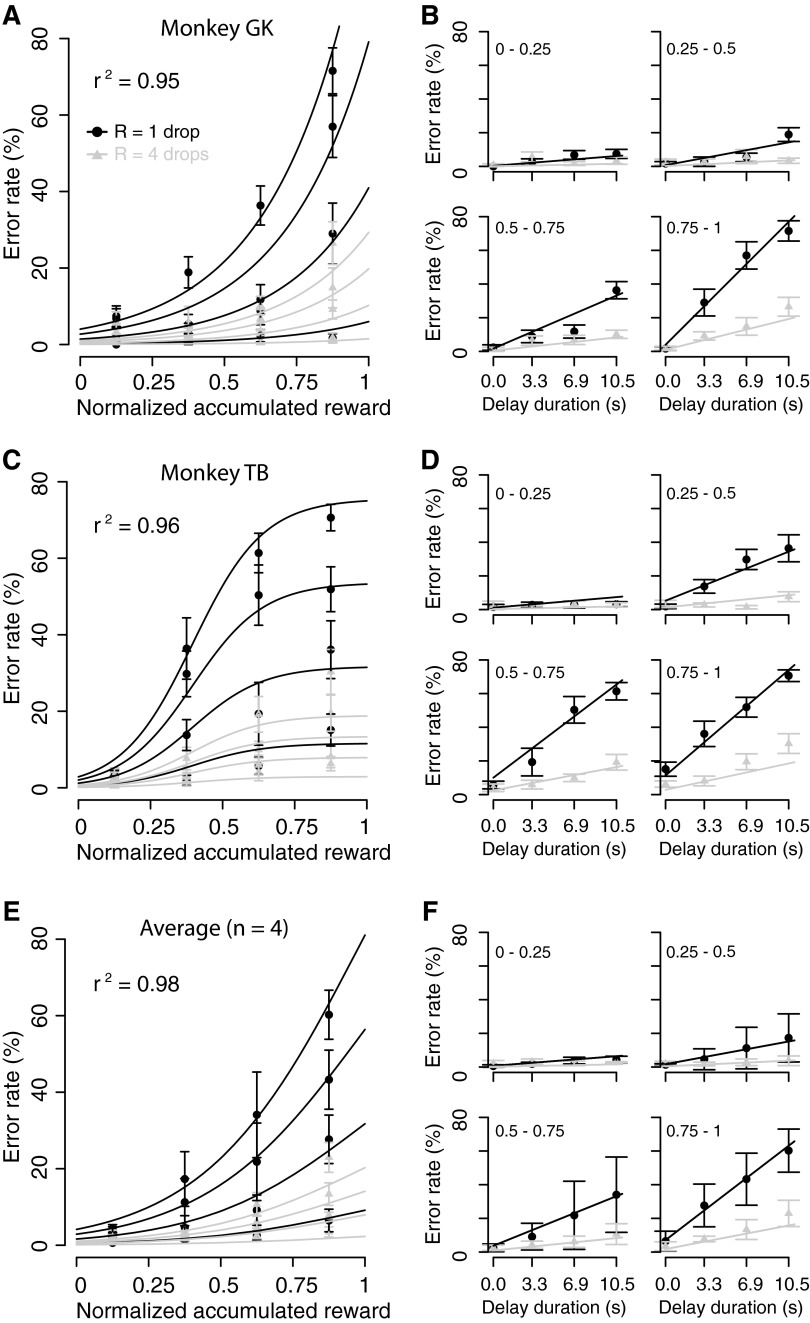
We performed the same analysis to examine the interactions among predicted reward size, delay-to-reward, and normalized accumulated reward simultaneously. The data from each session of the reward-size-and-delay task were divided into consecutive quartiles according to normalized accumulated reward (Eq. 4), and the error rates in each quartile were analyzed. When normalized accumulated reward was below one quarter (i.e., the monkeys should have been most thirsty), error rates were all low (Fig. 6, B and D, top left). As the normalized accumulated reward (and thus satiation level) increased, the overall error rate also increased (Fig. 6, B and D, from top left to bottom right). We modeled the relationship among error rate, reward size, delay-to-reward, and satiation level by combining Eqs. 2 and 6 into

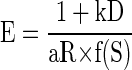(7)

FIG. 6.

Effect of relationship among predicted reward size, delay-to-reward, and normalized accumulated reward on error rate. A: percentage of error trials (mean ± SE) for each incentive condition as a function of normalized accumulated reward (A, C, and E) and as a function of delay duration for each quartile of normalized accumulated reward (B, D, and E, from top left to bottom right) in (A and B) monkey GK, (C and D) monkey TB, and (E and F) in the average across 4 monkeys. Black and gray circles correspond to 1 and 4 drops of reward, respectively. Black and gray curves and lines are the best fit of Eq. 7 to the data collected with 1 and 4 drops of reward, respectively.

The error rates were well explained by Eq. 7 for each individual monkey (r² > 0.89; Fig. 6, A and B, black and gray curves and lines; see also Supplemental Fig. S6) and for the average across monkeys (black and gray curves and lines in Fig. 6, C and D; r² = 0.98). The best-fit parameters are reported in Supplemental Table S4.

Effects of predicted reward size, delay-to-reward, and satiation level on reaction time

Reaction time became short as predicted reward size increased (Fig. 7A). Reaction time increased as predicted delay duration increased, whereas it did not increase as the next-trial-delay duration increased (Fig. 7B). In the reward-size-and-delay task, reaction time also became longer significantly as delay duration increased in all monkeys (P < 10⁻¹⁰, 2-way repeated-measures ANOVA; Fig. 7C, left) and in average across monkeys (P < 10⁻⁴; Fig. 7C, right). However, reaction time was significantly shorter in small reward trials than in large reward trials in three of four monkeys (Fig. 7C) but not in average across monkeys (P = 0.38; Fig. 7C). Reaction time increased significantly as reward accumulated (P < 0.05, 2-way repeated-measures ANOVA) and as reward size decreased (P < 0.001) in all monkeys (Fig. 7D, left). There was a significant interactive effect (P < 0.05) between reward size and normalized accumulated reward on reaction time in all monkeys (Fig. 7D). Overall, the effect of reward size, delay-to-reward, and normalized accumulated reward on average reaction times had the same trend as that of error rates.

FIG. 7.

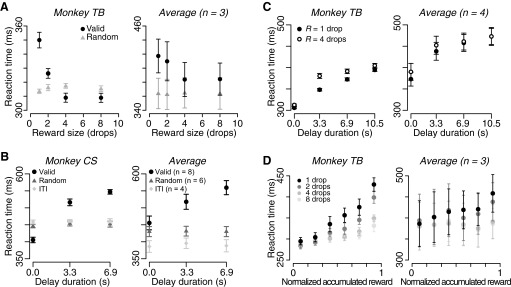
Effects of predicted reward size, delay, and normalized accumulated reward on reaction time. A: reaction time (mean ± SE) as a function of predicted reward size (left) in monkey TB and (right) in the average across 3 monkeys. B: reaction time (mean ± SE) as a function of delay duration (left) in monkey CS and (right) in the average across monkeys. Black circles, gray triangles, and light gray diamonds indicate valid cue condition, random cue condition, and the next-trial delay task, respectively. Number in parentheses represents the number of subjects. C: reaction time (mean ± SE) as a function of delay duration for each reward size (filled and open circles for 1 and 4 drops, respectively) (left) in monkey TB and (right) in average across 4 monkeys. D: reaction time (mean ± SE) for each predicted reward size as a function of normalized accumulated reward (left) in monkey TB and (right) in average across 3 monkeys.

DISCUSSION

To estimate the motivational value that reflects both external incentives and internal drive, we introduced a nonchoice paradigm in which different trial types are defined by different rewarding properties, like in a choice task, but the different rewards are offered in separate trials requiring the completion of the same action regardless of trial type. Thus the sensory and motor demands are held constant across all trials. Different trial types are parameterized by reward size and delay-to-reward, both of which can be predicted by association with a visual stimulus (valid cue). The presence of visual cues allows the monkeys to predict the current trial type, so that their behavioral reaction can be modulated quickly on a trial-by-trial basis, like in a choice task. The internal state of the animal changes slowly as a function of a gradual shift from thirst to satiation. The fraction of incorrectly completed trials and the reaction times can be used as direct correlates of the motivational value the animal assigns to each trial type in the face of its internal drive state. We found that error rate was inversely related to reward size and directly increased by delay-to-reward (hyperbolic discounting of reward value). Error rate in each trial type also depended on the (normalized) accumulated reward, which we took as a correlate of satiation level.

Error rate as a reflection of motivational value

Monkeys can perform the basic operant trials with few errors in the random cue condition. Based on this observation, we regard the excess error trials in the valid cue condition as trials in which the monkeys are not motivated enough to perform correctly. Thus we take the error rate as a direct, trial-by-trial reflection of the current motivational value of each trial.

Another measure that has been related to motivation is reaction time in correct trials (Cromwell and Schultz 2003; Hollerman et al. 1998; Minamimoto et al. 2005; Roesch and Olson 2004, 2005; Tsujimoto and Sawaguchi 2007). Reaction times seem to be related to motivation here also. However, the relation between reaction times and the measured parameters (reward size, delay-to-reward, and normalized accumulated reward) seems more variable than the relation between the error rates and the measured parameters. We suggest that this might occur because reaction time data can only be collected in successful trials, when the monkeys have already reached the motivational threshold to act.

The distributions of bar release times are markedly different for error trials than for correct trials: wider with a peak (often around cue onset) and a pronounced tail in error trials (Supplemental Fig. S2A), whereas much narrower and characteristically bell-shaped for correct trials (Supplemental Fig. S2B; see also Bowman et al. 1996). This comparison may indicate that error trials are not correct trials gone awry (i.e., the consequence of a “mistake” in releasing the bar due, e.g., to poor motor control). Instead, error and correct trials could be different actions, each determined by a different level of motivation, consistent throughout most of the trial as a function of the incentive condition (i.e., the distributions for different reward sizes in Supplemental Fig. S2 do not cross). In other words, we believe that error trials are the consequence of lessened motivation and not, for example, of lessened motor ability or lessened attention.

There is a reliable difference in the patterns of error rates observed in the valid versus the random cue condition. In the random cue condition, the error rates are uniform and only slightly higher than the error rates in the most rewarded (Fig. 2) or immediately rewarded trials (Fig. 3) in the valid cue condition. Overall, the total error rate is higher with valid cues. The same pattern was found in the reward schedule task (La Camera and Richmond 2008). This finding seems to imply that the monkeys are generally more motivated in the random cue condition. However, a reinforcement learning model of the reward schedule task (La Camera and Richmond 2008) explains the difference in total error rates not as the consequence of a different overall motivation in the two paradigms, but as the consequence of the average value being closer to the flat tale than to the inflection point of the “policy” function (the function that maps the motivational value of each trial into the probability of performing correctly).

Motivational value in free operant and choice tasks

Other ways of measuring the value of a reinforcer involve the use of free operant and choice tasks. Free-operant tasks, wherein animals perform repeatedly a simple action (key pecks for pigeons or bar presses for rodents) to obtain a reward, provide a means to study motivation using measures of performance (Killeen and Hall 2001; Skinner 1966), However, in these paradigms, it is difficult to measure the incentive effect of external factors rapidly changing (e.g., on a trial-by-trial basis). Choice tasks allow the assessment of the relative preferences of a subject and is commonly used to compare the relative values of different reward contingencies and other incentive effects (Kahneman and Tversky 2000; Samuelson 1937). However, although it is reasonable to assume that an animal will work harder for a preferred option, there is no clear means of converting the choice behavior into how hard or accurately will the animal work for the preferred option, when this is offered in isolation in exchange for some instrumental effort. That is, knowing that choice A is preferred over B does not provide any means to know how much effort the animal would expend to obtain A when presented alone.

The element of choice tasks that more closely reflects motivational value is, as in the task introduced here, those error trials that are not the consequence of an incorrect choice (where the correct choice is defined by the requirements of the task). A saccade to a right target in a trial requiring a saccade to the left is an example of a correctly executed trial where the wrong choice (according to the rules of the task) was made. On the other hand, trials aborted by the monkeys because of breaking eye fixation before the choice targets appear or because of the incorrect manipulation of a device (e.g., a joystick or a lever) used for making the choice are proper examples of what we have called error trials in this study (in the reward schedule task and in the task introduced here, these are the only types of error trials). It seems reasonable to assume that these aborted trials are the trials that reflect low motivation, e.g., because the reward is not currently worth the effort needed to obtain it. It is common to ignore this type of error trials in choice behavior, because preference value (only accessible in correct trials) is what is usually sought in a choice paradigm. Even though motivation to act is not the same as choice preference after a commitment to act has been made, it is reassuring that the effect of value on performance can be summarized using the same functional relationship as in intertemporal choice tasks (Mazur 1984, 2001). This relation is typically formulated as the inverse of Eq. 2

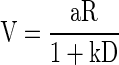(8)

where V stands for subjective value of the reinforcer.

Role of the internal state

Taken together, subjective value, preference value, and any other perceived value of a reinforcer all contribute to the motivational value of the reinforcer. The motivational value, however, is also affected by internal state. It is known that the internal state of the animal (e.g., hungry vs. sated) would energize or discount any action (also those not directly goal related) in a generalized manner (Hull 1952; Spence 1956; Toates 1986). Thus a more accurate definition of motivational value is one that accounts for both the predicted value of a preferred reinforcer and our current propensity to care for such value, i.e., our internal drive. The latter is more difficult to manipulate than visual stimuli predicting reward.

In our analysis, by monitoring one such variable, accumulated reward, we were able to account for it. We found that, as the animal proceeds from thirst to satiation, the effect of satiation level can be inferred from the performance to be sigmoidal and multiplicative. That is, when reward size, delay-to-reward, and satiation level are present simultaneously, their effects on motivational value (MV) simply multiply one another

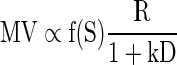(9)

Equation 9 is of the form MV = h₁(R)h₂(D)h₃(S), where the h_i are functions of a single argument, and thus shows that the effects of the external (R,D) and internal (S) factors on motivation are separable in three multiplicative contributions, each one depending on a single factor only. This multiplicative property is consistent with some of the implications of previously hypothesized theories of motivation (Hull 1952; Spence 1956).

The discounting factor, k, which in temporal discounting models describes the impact of delay on reward value and determines the slope of the decay function, was assumed constant and independent of satiation level. Good fits of the inverse of Eq. 9 to the data and previous studies showing that altering water deprivation level had no effect on choice preference between delayed and immediate rewards (Logue and Peña-Correal 1985; Richards et al. 1997) are consistent with this assumption. We chose a sigmoid function for the discounting effect of satiation on motivational value (see Eq. 5). It has been shown that free drinking behavior in water-deprived monkeys is controlled by many factors acting on different time scales, such as cellular dehydration, intestinal stimulation by water, gastric distension, and oropharyngeal metering (Gibbs et al. 1981; Maddison et al. 1980; Rolls and Rolls 1982; Wood et al. 1980). The quality of the sigmoid function fit to our data shows that the collective effects of all these factors on the behavior can be described with a simple phenomenological model. Finally, we note that our measure of satiation level might in principle also depend on factors that are likely to covary with satiation level, such as fatigue or boredom. Nonetheless, we believe that the effect of these other factors is small compared with the effect of satiation level.

Conclusions

Functionally, we related motivational value to the percentage of trials that are not completed correctly. We make this relation based on the knowledge that the monkeys are capable of performing the basic operant trials of the task at a very high level (cf. the random cue condition), yet they fail to do so when able to predict the forthcoming contingency (i.e., in the presence of valid cues). We have characterized the relation among two external factors, delay-to-reward and reward size, one internal factor, satiation level, and motivational value as Eq. 9: the reward size is linearly related to motivational value, the delay-to-reward is hyperbolically related to motivational value, the amount of accumulated reward is sigmoidally related to error rate, and the relations among these are simply multiplicative.

Motivational value is different from motivational level: the latter is the ability of a reinforcer to support any type of responding (Mazur 2001) and is slowly modulated by internal factors such as satiation level, whereas motivational value may depend also on incentive factors and thus be modulated on a faster, trial-by-trial, basis. Motivational value is also different from what is usually referred to as subjective value, which corresponds to the perceived value of a reinforcer when its incentive salience is changed because of external factors only (e.g., to reward size and delay-to-reward) (Green and Myerson 2004; Mazur 1984, 2001). Compared with motivational level and subjective value, the concept of motivational value offers a more complete account of what moves us to action in the presence of both incentive and internal driving forces. Motivational value is also affected by other variables that were either controlled for or absent in this study, such as different performance costs or changes in context (La Camera and Richmond 2008). We have provided a formal mathematical description of motivational value in monkeys performing a novel reward-discounting task, where reward size and delay-to-reward are independently manipulated and as the monkeys’ internal state proceeds from thirst to satiation.

GRANTS

This study was supported by the Intramural Research Program of the National Institute of Mental Health. T. Minamimoto was partly supported by a Japan Society for the Promotion of Science Research Fellowship for Japanese Biomedical and Behavioral Researchers at the NIH.