Models of coding sequence evolution

Abstract

Probabilistic models of sequence evolution are in widespread use in phylogenetics and molecular sequence evolution. These models have become increasingly sophisticated and combined with statistical model comparison techniques have helped to shed light on how genes and proteins evolve. Models of codon evolution have been particularly useful, because, in addition to providing a significant improvement in model realism for protein-coding sequences, codon models can also be designed to test hypotheses about the selective pressures that shape the evolution of the sequences. Such models typically assume a phylogeny and can be used to identify sites or lineages that have evolved adaptively. Recently some of the key assumptions that underlie phylogenetic tests of selection have been questioned, such as the assumption that the rate of synonymous changes is constant across sites or that a single phylogenetic tree can be assumed at all sites for recombining sequences. While some of these issues have been addressed through the development of novel methods, others remain as caveats that need to be considered on a case-by-case basis. Here, we outline the theory of codon models and their application to the detection of positive selection. We review some of the more recent developments that have improved their power and utility, laying a foundation for further advances in the modeling of coding sequence evolution.

INTRODUCTION

Models of molecular sequence evolution have diverse applications, from phylogenetics to genome annotation and comparative genomics. Although early models of sequence evolution achieved significant simplification by assuming that nucleotide sites evolve independently [1, 2], more realistic models have been proposed to take a range of different sources of context dependency into account [3, 4]. One of the most obvious sources of context dependency derives from the triplet nature of the genetic code. It is this dependency that is accounted for by codon models, which treat triplets of nucleotides as the states of the probabilistic process describing the evolution of a protein-coding sequence. Models that account for this have been shown to provide a substantially improved fit to protein-coding sequences [5, 6].

The degeneracy of the genetic code suggests a natural classification of codon substitutions, depending on whether they change or do not change the encoded amino acid (nonsynonymous and synonymous substitutions, respectively). The proposition that synonymous substitutions are generally neutral leads to the description of codon evolution as a combination of substitutions at the nucleotide level, and selective constraints operating at the protein level [7]. Codon models have distinct parameters describing the mutational and selective components of the substitution process, providing a means to assess the selective forces acting on a protein. Many of the applications of codon models relate directly to this capacity to quantify the strength of selection. Three types of selective pressures are frequently considered. When the rate at which nonsynonymous substitutions accumulate is lower than the rate of synonymous substitution, this is normally taken to imply that, on average, nonsynonymous substitutions have a negative effect on fitness. This is frequently referred to as purifying selection. A nonsynonymous substitution rate which is equal to the synonymous rate is consistent with neutral evolution, or the absence of selective constraints acting to preserve features of the encoded protein, when the rate of nonsynonymous substitution is greater than the rate of synonymous substitution this implies that, on average, nonsynonymous mutations confer a selective advantage and increase in frequency through positive selection. Thus, a comparison of the rate of nonsynonymous substitution to synonymous substitutions can provide evidence that a protein is evolving adaptively.

Codon models are very frequently used to identify protein-coding sequences evolving under purifying or positive selection pressure. Evidence of purifying selection pressure is useful for distinguishing coding from noncoding genomic regions, when orthologous sequences are available [8]. Any putative protein-coding sequence with a nonsynonymous substitution rate significantly lower than the synonymous rate can be inferred to be translated, and is likely to be functional. The ratio of nonsynonymous to synonymous substitutions also allows the strength of selection to be quantified and compared between different genes or gene copies. On the other hand, the identification of sequences or subsets of sites within a sequence evolving adaptively can provide information about key evolutionary processes and innovations. Because the effects of selection are very different at distinct sites in a sequence the question of how best to model site-to-site variation in parameters describing selective constraints receives particular attention. We review two trends in this regard, distinguished by whether sites are considered to belong to distinct site classes with fixed parameter values or whether the parameters themselves are described by random variables. These alternatives are referred to as fixed effects likelihood (FEL) and random effects likelihood (REL) models, respectively.

In this review, we outline the development of phylogenetic models of codon evolution with a focus on the use of these models to identify sites or lineages evolving adaptively. We consider recent advances leading to improved model realism, including the development of novel techniques to model sequence heterogeneity and a movement to integrate population genetics concepts into models of molecular evolution. Several caveats for the application of codon models are considered and we outline some of the solutions that have been proposed to address these concerns.

Probabilistic models of molecular sequence evolution

The modeling of molecular evolution has been facilitated largely by the development of an efficient means of calculating the likelihood [9] of an alignment, given a hypothesis of the phylogenetic tree relating the taxa in the alignment and an appropriate probabilistic model of the substitution process. These models generally take the form of a continuous time Markov process in which mutations are modeled along the branches of a phylogenetic tree, according to a rate matrix, Q, with elements (q_ij) describing the instantaneous rate of substitution from state i to state j, where the states may be nucleotides, amino acids or codons. Elements vary with model definition, yet typically make use of three parameter types: (i) frequency parameters, (ii) exchangeability parameters and (iii) rate heterogeneity parameters [7]. Both nucleotide and amino acid models of molecular evolution, and the methodological details of maximum likelihood phylogenetics, have been extensively reviewed elsewhere [1, 2, 10–13]. Codon models have previously been reviewed [1, 13], though not some of the more recent developments in the field.

Codon models have an alphabet of 64 states, typically reduced to 61 after removal of the three stop codons in the common genetic codes. The most general parameterization is [14]:

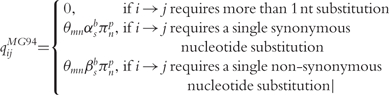where following Kosakovsky Pond et al. [14], θ_mn describes the relative exchangeability of nucleotide m for n (θ_AG = 1). 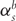is a parameter proportional to the rate of synonymous substitution, indexed by site in the alignment, s, and branch of the phylogeny, b, in the formulation presented here. Similarly, 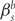is a parameter proportional to the rate of nonsynonymous substitution, similarly indexed, and 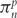is the equilibrium frequency (usually estimated directly from the empirical data rather than optimized as a model parameter) of the target nucleotide n (i.e. the nucleotide that differs between codons i and j) at codon position p (p ranges from position 1 to position 3 of the triplet codon) [15]. The parameters θ_mn are typically chosen from the range of standard nucleotide models, with the HKY85 [16] and general time reversible (GTR or REV) models [17] being popular. It is worth noting that the appropriate model choice depends primarily on data set size rather than on biological considerations: for large data sets the more parameter-rich models (e.g. GTR) tend to be appropriate, while small data sets necessitate the use of less detailed models.

An alternative parameterization of the codon model [18] is obtained by letting substitution rates be proportional to the frequency of the target codon rather than the position-specific frequency of the target nucleotide as in the Muse–Gaut (MG) [15] implementation. We use the terms Goldman–Yang (GY) and MG to denote these two alternative model assumptions. In the Goldman and Yang [18] parameterization, codon frequencies are estimated from the data either as the product of the frequencies of the 3 nt that make up the codon (referred to as F1 × 4), or as a product of position-specific nucleotide frequencies (F3 × 4). These estimates of equilibrium codon frequencies are more robust than an empirical count, since a very large amount of data would be required to provide a good estimate of the true equilibrium codon frequencies. However, actual counts can also be used, or codon frequencies can be treated as free parameters to be estimated. We evaluated the relative performance of the MG [15] versus GY [18] model assumptions, by fitting them to published datasets (Table 1) and comparing log likelihoods. Both implementations used the general time reversible model as the underlying nucleotide model, empirically estimated position-specific nucleotide frequencies (individually for MG and multiplied together as F3 × 4 estimates for GY) a discrete distribution for 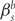, corresponding to M3 in Ref. [19] and constant 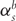. In all cases the MG model assumption outperforms the GY assumption (Table 1). This is consistent with recent Bayesian model comparison results [20], in which the mechanistic assumptions of these models, and their respective performances, are discussed in detail.

Table 1:

Performance comparison of MG [15] and GY [18] codon model assumptions on previously published datasets

Data set	MG-GTR	GY-GTR
Abalone Lysin [85]	−4357.9	−4381.3
Primate COXI [86]	−12123.6	−12271.1
Vertebrate β-globin [16]	−3666.7	−3686.8
Drosophila adh [16]	−4593.7	−4648.5
HIV-1 env [16]	−1121.6	−1158.8

Detecting selection affecting specific sites

As formulated above, both the rate of synonymous substitution, 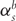, and the nonsynonymous substitution rate, 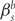, are allowed to vary across branches, b, and sites, s [19, 21–24]. In real protein-coding sequences, evolutionary rates vary substantially by position along the sequence and may vary by lineage; however, models allowing independent rates for all sites and all lineages would be severely over-parameterized. The choice of how to model heterogeneity in evolutionary rates provides an important distinction between alternative implementations of codon models. Earlier models treated evolutionary rates as random quantities described by parameterized distributions [19, 25], while some more recent models treat rates as a fixed effect but allow distinct classes of sites with independent parameters (including rate parameters). These two alternative approaches to modeling rate variation have been referred to as REL and FEL methods, respectively [26–28]. In both cases a nonsynonymous rate (dN) significantly greater than the synonymous rate (dS), or alternatively, ω = dN/dS significantly greater than one, points to positive Darwinian selection [29]. Sites at which this is the case are of particular interest and several implementations of codon models are extremely widely used to identify these sites (Box 1).

Box 1: Software implementations of codon models of evolution.

Software	Description		URL	Platforms supported
PAML	Phylogenetic statistical hypothesis testing	[97]	http://abacus.gene.ucl.ac.uk/software/paml.html	Linux Windows Mac OSX
HyPhy	Phylogenetic statistical hypothesis testing using existing and custom models	[98]	http://www.hyphy.org/	Linux Windows Mac OSX
PyEvolve	Phylogenetic statistical hypothesis testing using existing and custom models	[99]	http://cbis.anu.edu.au/software.html	Linux Windows Mac OSX
Datamonkey	Free web server implementation of various models in the HyPhy package		http://www.datamonkey.org/	Web server
Selecton	Free web server for sitewise detection of selection	[100]	http://selecton.tau.ac.il/	Web server
ADAPTSITE	Positive selection using counting methods	[101]	http://www.cib.nig.ac.jp/dda/yossuzuk/welcome.html	Linux Mac OSX
BEAST	Estimation of population parameters given uncertainty in the inference of phylogenies	[102]	http://beast.bio.ed.ac.uk/	Linux Windows Mac OSX
MrBayes	Bayesian phylogenetics software with codon models for positive selection detection	[48]	http://mrbayes.csit.fsu.edu/	Linux Windows Mac OSX

The simplest random effects models use a constant rate of synonymous substitution and approximate the sitewise variation in nonsynonymous rates using a three category discrete distribution accounting for purifying selection (ω < 1), neutrality (ω = 1) and positive selection (ω > 1) [30]. A test of positive selection can be obtained by comparing the likelihood under a model where the positive selection component (ω > 1) of this distribution has zero weight to the likelihood without this constraint (corresponding to a comparison of Wong et al.apos;s [30] models M2a and M1a). Since these models are nested, the distribution of the likelihood ratio test (LRT) statistic (Box 2) approximates a χ² distribution with degrees of freedom equal to the difference in the number of free parameters between the two models. For the above test, the difference in number of free parameters is two, one rate parameter (ω > 1), and a parameter describing the proportion of sites under positive selection and a conservative test can be obtained by comparing against a χ² distribution with two degrees of freedom. In fact, in this particular case, the LRT statistic is asymptotically approximated by an equal mixture of a χ² distribution with zero degrees of freedom and a χ² distribution with one degree of freedom (see [31, 32] for a discussion of one-tailed LRTs in phylogenetics). In addition to this approximation of the heterogeneity of ω across sites, other distributions have been proposed [19, 33]. Wong et al.apos;s [30] M1a versus M2a, and Swanson et al.apos;s [33] M8a versus M8, which models ω as a mixture of a beta distribution and point mass at ω = 1 in the null, and with ω > 1 in the alternate [33], are recommended for tests of positive selection. The characteristics of these and other suitable REL models are presented elsewhere [19, 23, 30].

Box 2: Statistical concepts and methods.

Concept	Description
Likelihood	The likelihood of a model (usually expressed as a function of its set of parameters) is the probability of observing the data, given the model parameters.
Maximum likelihood estimates (MLEs)	MLEs are fixed parameter values that maximize the likelihood of observing the data. Maximum likelihood (ML)-based methods use these fixed estimates, rather than averaging over multiple parameter values, as in Bayesian methods.
LRT	A classical hypothesis test for comparing the ML of a simpler model, L0 (e.g. excluding positive selection) which is nested within a more general model, L1 (e.g. including positive selection). The LRT provides an indication of whether the simpler model is inadequate to explain the data. Under L0, the LRT test statistic (2*(lnL1 − lnL0)) is χ2 distributed with degrees of freedom equal to the number of extra free parameters in L1 (see text for discussion).
AIC	An alternative ML-based model comparison technique that allows for comparison of non-nested models and that penalizes models according to the number of parameters, k (AIC = 2*k − 2 ln(L)).
Bayesian inference	Bayesian inference methods account for uncertainty in parameter estimates by performing a weighted average over possible parameter values. Bayesian methods require prior distributions for all parameters, which are typically assumed to be uninformative.
NEB	A post hoc analysis that uses the MLEs from a ML-based method to infer posterior probability distributions for parameters of interest. NEB assumes the MLEs are correct.
BEB	Similar to NEB in that MLEs are used to infer posterior probability distributions, but takes uncertainty in the MLEs into account.
MCMC	A sampling approach that can be used to approximate a probability distribution that is mathematically intractable. MCMC is often used in a Bayesian setting to estimate posterior probability distributions of model parameters.

The LRT provides a test of whether some sites in a sequence alignment are affected by diversifying selection, but does not identify specific sites at which ω is greater than one. In the case of REL models, empirical Bayesian methods (Box 2) have been used [25, 34]. Naïve empirical Bayesian (NEB) methods make use of maximum likelihood estimates of parameters describing the distribution of ω, inferred from the whole sequence, as a prior in order to estimate a posterior probability for each of the sites belonging to a site class in which ω > 1 [25]. The posterior probability that a site s, belongs to rate category k, is the product of the likelihood of the data at site s given the category k, L(D_s|ω_k), and the prior (P(ωs = ω_k), set to the inferred proportion of sites belonging to category k), normalized by the sum of site-specific likelihood for each category:

The posteriors, for each site and each rate category, are used to determine which sites are evolving under positive selection, given a posterior probability threshold. Since NEB uses the maximum likelihood parameter estimates of the distribution describing the sitewise variation in synonymous and nonsynonymous substitution rates as a prior, it is susceptible to inaccuracies in these estimates [35]. Potential solutions to this problem include a full Bayesian method for calculating posterior probabilities using Markov chain Monte Carlo (MCMC) [36, 37], and an approximate method, which accounts for some of the uncertainty in the maximum likelihood parameter estimates through averaging over a prior (Bayes empirical Bayes or BEB) [34, 38].

FEL methods provide an alternative to the REL models discussed above. These models treat sites as belonging to distinct classes, with independent parameters. In the extreme case, each site belongs to a separate class, requiring the estimation of a large number of free parameters, with the concomitant danger of over-parameterization [1]. When reasonable partitions of sites can be specified a priori, FEL models that allow separate parameters between these site classes may be useful [28]. For example, the a priori partitioning of MHC sites involved in the binding of foreign peptides [28] from other sites, allowed for the evaluation of positive selection independently for these classes. The degree to which parameters (including relative branch lengths, nonsynonymous substitution rate, synonymous substitution rate, transition–transversion rate ratio and codon frequencies) should be shared across these classes can be decided using model comparison techniques [26, 28]. Bao et al. [26] compared the use of the Akaike information criterion (AIC) [39], AICc [40] and a backward elimination procedure based on the LRT and found, from simulation, that the latter appeared to provide the best means of choosing the appropriate model. However, even when an a priori partitioning of sites into classes, based on protein folding, is available this is likely to model only a small proportion of the sitewise variation in the substitution process. Furthermore, power may be affected by sites which are conserved, yet occur within putatively positively selected protein domains [28].

An alternative to the use of a priori site classes, which may fail to model site-to-site variation adequately, and models that treat sites as completely independent, resulting in over-parameterization, can be obtained by the use of techniques that allow site classes to be inferred from the data. One approach is likelihood-based clustering (LiBaC) that allocates sites to classes by maximizing a mixture log likelihood, which takes account of uncertainty in site allocation by averaging over classes of sites. This model is implemented with an expectation–maximization (EM) algorithm that successively optimizes model parameters and adjusts a site allocation vector (a vector indicating site class membership for each site), given the proposed parameters. The LiBaC method showed significantly improved performance over REL models, especially when relative branch lengths differed between partitions [41]. Perhaps a limitation of the model is that the number of distinct site classes is chosen beforehand, by comparing the log likelihoods of REL models with different numbers of discrete components. An alternative to this is the use of Dirichlet process models, which have been applied in the contexts of modeling sitewise variation in the amino acid replacement process [42] or selection pressure using codon models [43]. Neither the site class membership nor the number of site classes is fixed, but is rather modeled as a mixture distribution using a Dirichlet process. This approach was adopted within a MCMC sampling framework to detect positive selection. The implementation accounted for uncertainty in the phylogeny and branch lengths resulting in a more conservative identification of positive selection than methods that first estimate these parameters and treat them as fixed in subsequent analysis [43].

Detecting selection affecting specific lineages

Codon models have been implemented that allow variable rates of evolution between lineages. Codon-based models that allow the rates of evolution to vary between lineages have been applied to assess evidence of adaptation affecting specific taxa or sets of taxa [44, 45]. In the earliest implementations, a separate value of ω was fitted along focal lineages which were specified a priori [44, 45], but without provision for site-to-site variation in selective pressure. Subsequent models that allowed site- and branch-specific selective pressure [23] were found to be subject to high false positive rates [46], although a modification of the original model showed improved levels of false positives [24]. Given a biologically plausible scenario, the prior specification of branches may be acceptable, but in many cases there may be no prior expectation regarding the selective processes that have affected different branches of the phylogeny. In such cases, each branch can be allowed an independent value (or distribution) of ω, but this approach requires corrections for multiple testing [21] with a corresponding loss of power. Given large phylogenies typically used in scans for lineage-specific positive selection, it is computationally impossible to test all possible alternatives of branch-specific selective regimes. Kosakovsky Pond et al. [22] provide a genetic algorithm alternative for model selection, in which AIC is used as a measure of fitness to select models with the most likely distribution of selective regimes among branches of the phylogeny [22]. The strength of this approach is that a larger population of potential models can be evaluated without the need for prior specification of lineages with alternate selective regimes. It has, however, been criticized for not providing a hypothesis test for the presence of positive selection [21]. The issue boils down to whether the traditional hypothesis testing framework, with its notion of statistical significance, is a more appropriate one in which to address questions such as these, than the alternative approach provided by criteria, such as the AIC. The latter attempts to quantify the strength of evidence for multiple models, none of which is assumed to be ‘correct’, rather than to measure the significance with which a specific (and possibly a priori unlikely) null hypothesis can be rejected. Both methodologies are statistically sound, and the debate about their relative merits has been conducted in a much broader context [47].

Caveats for application of codon models

Phylogenetic uncertainty

Thus far, we have assumed that the phylogeny on which we model molecular evolution is an accurate representation of the evolutionary history of the taxa. In general, even if we make the assumption that a true phylogenetic relationship between a set of sequences exists (i.e. the same relationship can be used to describe the entire length of the alignment, which is not true when recombination has occurred), then that relationship is unknown and must be inferred from the data. The usual approach is to infer a single tree and then base subsequent inference on that tree. Empirical results have indicated that inference of codon model parameters and/or positive selection is not very sensitive to tree topology, as long as ‘a reasonably good phylogeny’ (i.e. one that has been estimated from the data) is used [19].

Nevertheless, it is inevitable that using an incorrect tree would have some effect on inference. It is possible to account for uncertainty in tree topology using a Bayesian approach in which parameter estimates are averaged over the space of possible trees, weighted according to their individual posterior probabilities. A number of Bayesian phylogenetic software packages exist, of which MrBayes [48] is perhaps the most the commonly used one that supports codon models. Such methods relax the assumption that a specific tree is correct, but not the assumption that a correct, though unknown, tree exists. Perhaps a more important motivation for using the Bayesian approach is that, in addition to averaging over multiple plausible tree topologies, it also averages over multiple plausible parameter values, providing a natural way to take uncertainty in parameter estimates into account. The use of this approach for inferring positive selection was first demonstrated by Huelsenbeck and Dyer [36], and extended through the use of a Dirichlet process model [43] (as discussed above). Further evaluation of Bayesian models [37], demonstrated that some form of Bayesian approach (either a full Bayesian approach or the BEB method described above) is important for medium-sized data sets (e.g. 30 taxa, 100 codons, with a tree length of up to two substitutions per codon). However, the extra computational cost of the fully Bayesian approach as compared to BEB is unlikely to be justified except when analyzing data sets with very low divergence and hence low information content.

Recombination

When the sequences under consideration have recombined, it is no longer the case that there is a single phylogeny describing their evolution. Instead, different phylogenies are required to describe the evolutionary relationships of the segments of the alignment defined by recombination breakpoints. The standard practice of assuming that a single topology describes the entire alignment can lead to arbitrarily high false positive rates when inferring positive selection from recombining sequences [49, 50].

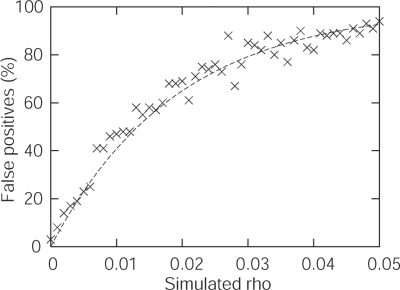
We illustrate this in Figure 1, which shows how the false positive rate increases as a function of recombination rate. These results were obtained using Codonrecsim [49] to simulate 100 neutrally evolving data sets (ω = 1 at all sites) with codon frequency parameters and transition–transversion rate ratio matched to the Hepatitis D virus antigen (HDV) data set used in one of the previous studies [49]. For each replicate data set, positive selection was inferred if there was a significant improvement in the likelihood of the selection model (M2a) over the neutral model (M1a). As the recombination rate (ρ) is increased, the false positive rate rapidly increases from below the acceptable level of 5% towards 100% (Figure 1). For a data set with parameters as described above, the significance level (α = 5%) is a reasonable estimate of the false detection rate only for ρ < 0.004. For ρ > 0.024, positive selection is more likely to be inferred than not, even if all sites evolve neutrally.

Figure 1:

The relationship between the recombination rate and the rate of false inference of positive selection in an example data set consisting of 10 taxa (using a population-scaled substitution rate of μ = 3.6, and a population-scaled recombination rate varying from ρ = 0 to 0.1 with increments of 0.002). Recombination rates are measured as ρ = 2Nr, where N is the effective population size and r is the number of recombination events per inter-codon link per lineage per generation. Hence, a recombination rate of ρ = 0.004 means that a given inter-codon link at a given lineage experiences, on average, one recombination event every 500N generations.

To illustrate the extent of the problem in real sequences, we constructed 10-taxon intra-subtype HIV-1 data sets of the env and gag genes and applied this simulation methodology. At the recombination rates estimated by the program LAMARC [51], we obtained false inference of positive selection in, respectively, 100 and 92 out of 100 replicates. This means that the apparent signature of positive selection in these sequences may have arisen as a result of recombination in the absence of positive selection, and that the recombination problem is therefore of practical rather than just theoretical importance.

One solution to this problem is a population genetics approximation to the coalescent which co-estimates recombination rate and selective pressure [52]. An alternative solution involves identification of recombination breakpoints and estimation of a separate phylogeny for each recombinant partition. The parameters of the codon models are then estimated in the usual way, except that phylogenies and branch lengths are partition-specific, while the remaining parameters are shared across all segments [53]. It also proved important to incorporate synonymous rate variation (see below) in this case, because recombination can cause an apparent variation in the synonymous rate [53]. Fortunately, the recombination breakpoints detected by off-the-shelf recombination detection tools appear to be sufficient to address the false positive problem, and may even give better results than when the true recombination breakpoints are known due to the fact that the recombination breakpoints that are difficult to detect typically have little effect on inference and can be ignored in order to estimate phylogenies on longer, more informative segments [53]. A similar approach [54] incorporates the breakpoints estimated, using a genetic algorithm for recombination detection (GARD), into a FEL selection analysis, suitable for the detection of individual adaptively evolving sites in recombined sequences.

Synonymous rate variation

In the application of codon models to detect selection, the synonymous substitution rate is often assumed to be constant across all sites in the alignment. Synonymous substitution rates may vary either because of site-to-site variation in mutation rates or because of selection acting to preserve functional motifs at the nucleotide sequence level. The latter, in particular, is now recognized as pervasive in protein-coding sequences [55]. Synonymous changes in protein sequences can cause, among many other effects, changes in the stability of mRNA secondary structure and formation or disruption of motifs that affect splicing (e.g. exonic splice enhancers) [56]. Codon models to detect synonymous rate variation applied to various published datasets revealed significant evidence of synonymous rate variation in 9 out of 10 cases tested and highlighted the likelihood of misleading inference of selection when this is ignored [57]. Indeed, a recent evaluation of a likelihood-based clustering method [41] demonstrated the false inference of positive selection with typical positive selection models (M2, M3, M8) when nonselective components (synonymous rate, transition/transversion rate ratio, relative branch lengths) of the substitution process are constant across sites. Selection on synonymous changes has been modeled explicitly when such selection is constant across all sites [58], (e.g. site-independent codon usage bias), but remains an issue for selection acting on only a subset of sites.

Recent modifications and extensions of codon models

Independence of sites

Traditionally, models of sequence evolution have included the assumption that distinct sites in a sequence alignment evolve independently. This significantly reduces model complexity and allows the likelihood to be calculated as the product over likelihoods of individual sites. However, site independence is an assumption that in many cases is grossly at odds with biological expectations. In real data, the rate of evolution is often autocorrelated along the sequence, with regions of conservation and rapid evolution. The combination of hidden Markov models to model rate variation along the sequence and phylogenetic models describing sequence evolution across taxa was introduced to model autocorrelation of evolutionary rates [4, 59] and subsequently adapted for use with codon models [60]. Interestingly, in an analysis of HIV-1 genes, dependency between adjacent sites was greater for synonymous than for nonsynonymous substitutions [60], potentially the result of tertiary structure, where nonsynonymous mutations co-vary at sites that are adjacent in the tertiary structure of the protein [12] and not necessarily adjacent in the primary sequence.

Models that allow autocorrelated rates are useful for accounting for local features of a sequence, allowing distinct functional classes and rate classes that are modeled as a Markov chain of hidden states. Functional interactions between sites can also be nonlocal, so that the rate and nature of sequence change at one site may depend on the state present at another site, which is not necessarily adjacent or close to the site under consideration. Examples of the latter include models of Watson–Crick pairs in RNA stem regions [61–63] or of interacting amino acids that maintain the stability of proteins [64–66]. The most general models of sequence evolution that set aside the assumption of independence of sites model whole sequences as the states in the continuous-time Markov process, resulting in rate matrices of extremely high dimension [64] (4^N × 4^N, where N is the sequence length). Robinson et al. [64] proposed a method to estimate such a model using a MCMC method to sample model parameters and to sample from possible sequence histories, proposed under a simpler evolutionary model (see [67] for an efficient method to sample from evolutionary histories). In a related development, Poon et al. [68] set out to identify interacting sites by reconstructing ancestral states under a codon model that assumed site independence and then estimated a Bayesian network from an array of branch-specific synonymous and nonsynonymous substitutions [68]. Interacting sites within the network are identified as those at which substitutions repeatedly co-occur along the same branch. This method has facilitated the identification of clusters of spatially separated codons that show dependent or compensatory mutations in HIV-1 [68].

Models with context dependency have also been used to account for elevated rates of mutation from cytosine to thymine at CpG dinucleotides [3, 69, 70], the result of spontaneous deamination of methylated cytosine [71]. These models, which account for CpG-context dependence both within codons, and across codon boundaries, have demonstrated the significance of CpG hypermutation within protein-coding genes [3, 70]. In the context of viral evolution CpG gain and loss is modeled [72] since unmethylated CpG dinucleotides may trigger a host immune response [73], or increased methylation at CpG sites may negatively affect viral gene expression [74]. Thus these models need to consider selective constraints operating at the amino acid or codon (codon usage bias) levels as well as the mutational effects and potentially selective effects of CpG dinucleotides at the nucleotide level.

Linking models of sequence evolution to population genetics

The models of sequence evolution presented above are typically applied to alignments of coding sequences from multiple species and encompassing evolution over long timescales. These models are concerned with the rates at which specific substitutions occur and, in turn, these rates are influenced by the rate of mutation and by selection. Recently there has been an upsurge of interest in relating parameters of sequence evolution models to the quantities that are of interest in population genetics, such as fitness and associated fixation probability. This work builds on a model of codon evolution that included separate terms for the probability of a mutation and the probability of fixation of a newly arisen mutant allele [75]. In the original application, this approach was used to model position-specific frequencies of amino acids in order to estimate evolutionary distances more accurately. More recently, a conceptually similar approach has been applied to estimate the distributions of selection coefficients associated with mutations in 5S ribosomal RNA [76, 77] and of substitutions between synonymous codons [58]. These studies not only bridge the gap between sequence models and population genetics, but also include phenotype quantitatively in the sequence model, adding considerably to the scope and potential applications of sequence models.

Selection on codon usage can result from differences in translation speed and accuracy between synonymous codons (see [78] for a review). Standard codon models, which include parameters describing codon equilibrium frequencies, can be used to infer positive selection even with strong codon usage bias, regardless of whether the bias is mutational or due to selection [79]. The novel codon model, FMutSel, proposed by Yang and Nielsen [58], separates out the selective and mutational components of codon usage bias. By comparing the fit of this model to a restricted form that models only the amino acid frequencies, the authors estimate the strength of selection acting on codon usage in large sets of mammalian genes. FMutSel shows a significantly improved fit to real data over standard codon models, but is parameter rich, requiring separate parameters to be estimated for every codon in its full form; however, use of empirical rather than estimated parameters appears to have only a marginal effect on model likelihoods and parameter estimates [58].

Integrating empirical and mechanistic models of codon evolution

Although codon models generally fit protein-coding sequence data far better than nucleotide models, at the basic level they take no account of the nature of the encoded amino acids and instead treat all nonsynonymous substitutions as selectively equivalent. Given the differences in the physical and chemical properties of amino acids, this omission leaves a substantial proportion of the evolutionary process unmodeled. In functionally conserved regions of an amino acid sequence, for example, replacement of one amino acid with another with similar properties may have a much smaller negative effect on fitness than replacement with a radically different amino acid. Models of amino acid sequences based on observed replacements in closely related and reliably aligned sequences have been in widespread use since the since the 1970s [80]. Because they are based on real data these empirical models naturally account for aspects of the amino acid properties that affect the likelihood of amino acid replacement. The empirical models also reflect mutational differences between pairs of amino acids implied by the genetic code; however, in this framework it is not possible to separate out the mutational and selective forces.

Considering the advantages of the mechanistic approach taken by codon models and the value of the empirical information contained in amino acid models, it is natural to investigate methods for combining these approaches. Kosiol et al. [81] proposed an empirical model for codons, and estimated nearly 2000 free parameters describing the empirical exchangeabilities of pairs of codons, assuming reversibility, from a large database of aligned-coding sequences. They incorporate these estimated codon exchangeabilities into the framework of standard mechanistic models of codon evolution and find that they generally provide a significantly improved fit to real data. In an alternative approach Doron-Faigenboim et al. [82], developed a method to incorporate a given empirical amino acid replacement matrix into the mechanistic framework. Again the combined empirical and mechanistic model provides a greatly improved fit to real data. In contrast to standard mechanistic codon models, both models are implemented such that they allow nonzero instantaneous rates of substitution between pairs of codons differing at more than 1 nt position. Although interpretation of the ω parameters is more difficult in the case of both of these models, it is possible to use the merged empirical and mechanistic models to infer positive Darwinian selection, though whether they have a power advantage over standard methods in this application is unclear. Another potential application of these models is to phylogenetic inference, where the improved model realism may offer a substantial advantage [81, 82]. In general, the use of codon models in phylogenetics incurs a significant computational cost due to the number of free parameters to be estimated and due to the size of the instantaneous rate matrix. Despite these costs, codon models show improved model fit over both standard nucleotide models, and nucleotide models which have codon position-specific nucleotide frequencies [6], suggesting that codon models are highly appropriate for phylogeny estimation.

CONCLUSIONS

The trend towards increasingly biologically realistic models and associated increase in the numbers of free parameters to estimate carries a risk of over-parameterization [1]. Perhaps a better alternative to maximum likelihood methods in this context is provided by Bayesian methods, which are generally better suited to large parameterizations [83]. The Dirichlet process [42, 43] that allows the data to influence the complexity of the model (in this case the number of distinct site classes) is useful in this regard. In addition to variable evolutionary rate parameters, models are being proposed that relax the assumption that all sites share a set of character state equilibrium frequencies. Relaxing this assumption can be useful, for example, to model distinct amino acid profiles [42], or fitness landscapes across sites [84]. Directional selection models, which have been applied in the context of the evolution of drug resistance [85], or antigenic drift associated with host-immune pressure [84, 86] also go beyond modeling only evolutionary rates and instead consider fitness effects associated with mutations involving specific amino acids. Nonetheless, these models generally still assume a fitness landscape that is constant in time, despite varying across sites. Stationarity is the assumption that the Markov process, along with its nucleotide, codon or amino acid frequencies, does not change over time. This implies that the process is at equilibrium, so that the observed frequencies of the states of the Markov process are also the equilibrium frequencies. Similarly, rates of substitution are assumed to be time homogenous. Nonstationary models have been applied in the nucleotide and amino acid contexts, specifically for the estimation of phylogenies when base compositions vary between closely related taxa [87–92]. Furthermore, selective constraints are likely to change over time [93–95], such that codon models incorporating variable selective pressure offer improved model fit [96]. Given that adaptive evolution, almost by definition, implies a process which is both directional and time heterogeneous, realistic descriptions of time-variable directional selective pressures will be of particular interest in models that seek to understand how adaptation shapes the evolution of molecular sequences.

Key Points.

• Phylogenetic models of sequence evolution typically make use of the formalism of the continuous-time Markov process and are in widespread use in molecular evolution.

• Models treating the 61 sense codons as the states of the process (codon models) have the advantage of capturing both the mutational process operating at the nucleotide level and selective processes operating at the protein level.

• These models are used to detect selection within genes, at sites within genes, along lineages and at sites along lineages.

• Caveats concerning the use of codon models to estimate evolutionary selective pressures acting on protein-coding sequences have recently been highlighted. Some of these, including uncertainty in phylogeny and parameter estimates, and sequence recombination have been addressed through the development of new methods.

• Further developments have improved the biological realism of codon models, including integration of codon models with empirical amino acid models that help to account for amino acid properties.

• More recently, models have been developed that allow interactions between sites and include parameters describing fitness. The latter go some of the way towards bridging the gap between models of sequence evolution and population genetics theory.

• Future developments in codon models may include further relaxing assumptions such that temporal heterogeneity in both mutational and selective processes can be modeled.

FUNDING

South African National Bioinformatics Network.

Biographies

Wayne Delport is a postdoctoral associate with an interest in modeling evolution, particularly with applications in human health and pathogen evolution.

Konrad Scheffler is a lecturer in Computer Science at the University of Stellenbosch, and focuses on probabilistic models of evolution.

Cathal Seoighe has been at the University of Cape Town since 2004 and was previously at the University of the Western Cape. He has research interests in molecular evolution, HIV-1 and mRNA splicing.