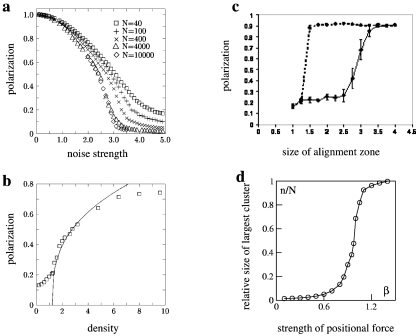
Figure 2. Transition from disorganized to organized collective motion as a function of the model parameters.

The quantity used to pinpoint the transition is the polarization, or global alignment, defined as the modulus of the average normalized velocity of the group $1∕N\mid {\sum }_{i=1}^N{\vec{v}}_i\mid$. In the Vicsek model only alignment is considered and the only two relevant parameters are the noise strength and density, defined as the number of individuals N divided by the whole volume of the simulation box. (a) Polarization as a function of the noise strength: for low noise a coherent moving group (large polarization) is present. (b) Polarization as a function of density: increasing density triggers the transition to collective motion. Reprinted figures from Vicsek T et al., Phys. Rev. Lett.75, 1226 (1995). Copyright 1995 by the American Physical Society. Reprinted with permission of the American Physical Society. (c) Change in polarization as the size of the zone of alignment is increased (bold line) or decreased (dotted line). Reprinted from Couzin ID et al., “Collective memory and spatial sorting in animal groups,” Journal of Theoretical Biology218, pp. 1–11. Copyright 2002, with permission from Elsevier. In this model the authors consider three distinct behavioral zones for repulsion, attraction, and alignment, plus a blind volume behind the focal individual. Only for large enough values of the alignment zone can the collective state be achieved. The degree of alignment depends on the increase∕decrease protocol used (hysteresis), which is typical of first order transitions. (d) Transition from a dispersed gas-like aggregation to a cohesive group in the model of Gregoire et al. (2003), where attraction/repulsion forces are used together with alignment of velocities. The figure shows the relative size of the largest cohesive cluster (number of individuals belonging to the cluster divided by total number of individuals) as a function of the strength of the attraction∕repulsion force. Reprinted from Gregoire G et al., “Moving and staying together without a leader,” Physica D181, pp. 157–170. Copyright 2003, with permission from Elsevier.