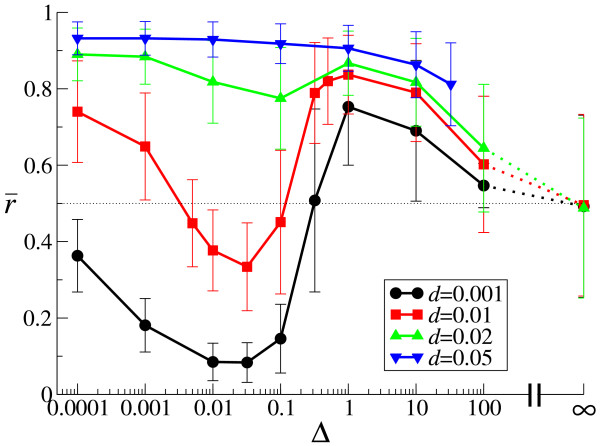
Figure 3.

The evolution of strand preference (r) as a function of diffusion intensity (Δ). The population mean of r ($\overline{r}$) is plotted as a function of the diffusion intensity (Δ) for various decay rates (d). Error bars show the mean absolute deviation of r in a population, which is defined as ADev(r) = ∑_i|r_i - $\overline{r}$|/N where N is population size, and i denotes an individual. Both $\overline{r}$ and ADev(r) were averaged over time after the system reached equilibrium. The other parameters than Δ and d are the same as in Fig. 2. For computational reason, the data for Δ = 100 are obtained from a field of 100 × 100 squares (note that diffusion will be effiectively stronger in a smaller field). The data for great values Δ are not plotted for d = 0.05 since the system goes extinct (this is because of the fluctuation in $\overline{r}$, which is due to the system size being finite).