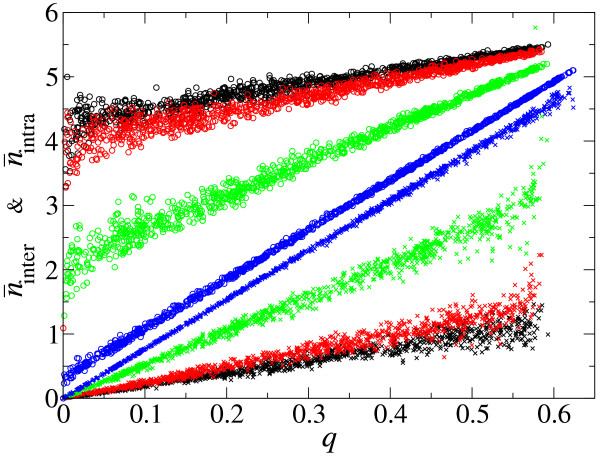
Figure 5.

The degree of spatial correlation within same species and between different species as a function of the density of observed species. ${\overline{n}}_{\text{intra}}$ (circles) is the average number of molecules of the same species that a given molecule "meets" in a single time-step (i.e. that are in its neighborhood) (see main text for details). The abscissa (q) is the density of the same species, which is calculated as the number of individuals of that species divided by the total number of squares on the grid. ${\overline{n}}_{\text{inter}}$ (crosses) is the average number of molecules of the opposite species that a given molecule meets in a single time-step. The abscissa (q) is the density of the opposite species, which is calculated in a manner similar to the case of ${\overline{n}}_{\text{intra}}$. The two species are identical with respect to the parameters, and both have r = 1/2. Colors represent diffusion intensity (Δ): Δ = 0.001 (black); Δ = 0.01 (red); Δ = 0.1 (green); Δ = 1 (blue). The rate of decay (d) is 0.05. Mutation is disabled (μ = 0). The other parameters are the same as in Fig. 2.

A tentative explanation for why ${\overline{n}}_{\text{intra}}$ is a linear function of q can be given as follows. Because of the local reproduction, when a species exists, it always exists on the grid as aggregates. Therefore, an individual always "meets" some number of individuals of the same species no matter what the density of the species in a whole system is (α > 0). When an aggregate "meets" with other aggregates, then the individuals will see more individuals of the same species, which increases ${\overline{n}}_{\text{intra}}$. Given that the aggregates are randomly distributed on the grid, the chance of an aggregate meeting with another aggregate is proportional to the number of aggregates in the system, which is proportional to the total density of the species (q). Therefore, ${\overline{n}}_{\text{intra}}$ is a linear function of q. Because of the symmetry, ${\overline{n}}_{\text{inter}}$ is also a linear function with the same slope as ${\overline{n}}_{\text{intra}}$ (but the intercept must obviously be 0 for ${\overline{n}}_{\text{inter}}$.