Abstract
The vast majority of parallel transmission RF pulse designs so far are based on small-tip-angle (STA) approximation of the Bloch equation. These methods can design only excitation pulses with small flip angles (e.g., 30°). The linear class large-tip-angle (LCLTA) method is able to design large-tip-angle parallel transmission pulses through concatenating a sequence of small-excitation pulses when certain k-space trajectories are used. However, both STA and LCLTA are linear approximations of the nonlinear Bloch equation. Therefore, distortions from the ideal magnetization profiles due to the higher order terms can appear in the final magnetization profiles. This issue is addressed in this work by formulating the multidimensional multichannel RF pulse design as an optimal control problem with multiple controls based directly on the Bloch equation. Necessary conditions for the optimal solution are derived and a first-order gradient optimization algorithm is used to iteratively solve the optimal control problem, where an existing pulse is used as an initial “guess.” A systematic design procedure is also presented. Bloch simulation and phantom experimental results using various parallel transmission pulses (excitation, inversion, and refocusing) are shown to illustrate the effectiveness of the optimal control method in improving the spatial localization or homogeneity of the magnetization profiles.
Keywords: parallel transmission, transmit SENSE, multidimensional pulse, optimal control, pulse design
Multidimensional spatially selective RF pulses (1–6) have been used in a wide range of MRI applications, including localized magnetization manipulation (7–10), magnetization profile improvement (11–14), and motion tracking and correction (15). These pulses are typically much longer than 1D slice-selective RF pulses (e.g., 15–160 ms), which can limit their effectiveness due to relaxation and off-resonance effects. Recently, parallel transmission of spatially selective RF pulses (16–18) has been shown to shorten pulse durations without sacrificing spatial resolution of magnetization profiles (16–25), as well as improve spatial excitation patterns (21), produce a more homogeneous excitation (22–24,26), and generate lowered power RF pulses (17,21,27,28). However, the vast majority of the design methods for parallel transmission pulses so far are based on a small-tip-angle (STA) approximation of the Bloch equation (1). These methods can design only excitation pulses with a small flip angle (e.g., 30°), and cannot design inversion/refocusing pulses. Even for 90° excitation pulses, it has been noted that STA-based parallel transmission pulse design can yield significant error in excitation profiles (18,29). In Ref. 30, we propose a noniterative method for designing large-tip-angle multidimensional pulses for parallel transmission, based on linear class large-tip-angle (LCLTA) theory (3). The LCLTA design generalizes the STA design in that the initial magnetization can be arbitrary. This property allows designing a large-tip-angle pulse through concatenating a sequence of small-excitation pulses when a special class of excitation k-space trajectories such as the inherently-refocused spirals is used (3). The LCLTA design equation is similar to STA except that the magnetization profile is replaced with the flip angle profile (3). Both STA and LCLTA are linear approximations of the nonlinear Bloch equations. For example, it has been shown that STA is only the first term in a perturbation expansion of the Bloch equation in powers of RF amplitude (31). As a result, imperfections due to the higher order terms can appear in the final magnetization profiles in the form of ripples and rounded edges, even when STA or LCLTA conditions are approximately satisfied. Large distortions from the ideal magnetization profiles can appear when STA or LCLTA conditions are violated, e.g., when using the STA method to design a 90° excitation pulse, or when only a small number of spiral turns are used for a 2D LCLTA 180° refocusing pulse (so that each subpulse is no longer a small excitation pulse). In such cases, it is necessary to derive RF waveforms directly from the Bloch equation.
Inverting the Bloch equation has been well investigated for 1D, single-channel RF pulses. Some of the notable methods include the Shinnar-Le Roux method (32), analytic solution of some special forms of RF pulses (33), neural networks method (34), evolutionary method (35), simulated annealing (36), perturbation response based method (37), iterative correction for hardware nonlinearity (38), SPINCALC (39), inverse scattering transform method (40,41), stereographic projection method (42), and optimal control (43,44). Due to its flexibility for systematically imposing desirable constraints (e.g., RF power) and richness in efficient algorithms, the optimal control method has been applied to several applications to design improved 1D, single-channel RF pulses. Some of the remarkable contributions to optimal control pulse design are the following: Conolly et al. (43) established the controllability of the MR spin system under selective RF pulses and formalized the 1D single-channel RF pulse design problem as an optimal control problem with three forms of cost functional (also called performance index). Murdoch et al. (45) first included a “jaggedness” term in the cost functional to penalize the discontinuity of pulses and used mathematical programming to solve the optimal control problem. Conolly et al. (46) generalized the optimal control theory to include complex RF waveforms. Rosenfeld and Zur (47) extended the optimal control theory to optimize adiabatic selective pulses in the “frequency frame” that rotates according to instantaneous frequency of the RF pulses. Skinner et al. (48) applied optimal control to broadband pulses for high resolution NMR. Ulloa et al. (49) mapped the Bloch equation onto the Chebyshev coefficient domain, thus converting the dynamic optimization problem to an algebraic optimization problem. Anand et al. (50) minimized specific absorption rate (SAR) over both RF and gradient waveforms, and included maximum gradient amplitude and slew rate constraints in their formulation.
In this work, we generalize optimal control for 1D, single-channel RF pulse design to the multidimensional, multichannel case. Compared to a recently proposed direct optimization approach (23), the approach in this work takes full advantage of the optimal control theory to explicitly update RF waveforms, and therefore has reduced computational complexity. Specifically, we first formulate the multidimensional multichannel RF pulse design as an optimal control problem with multiple controls and derive the necessary conditions for the optimal solution using calculus of variations. Based on these conditions, we use a first-order gradient optimization algorithm to iteratively solve the optimal control problem. We then present a systematic procedure to design multidimensional multichannel RF pulses with arbitrary flip angles using optimal control. In the results section, we first demonstrate the effectiveness of optimal control to improve various types of pulses (designed by existing methods) by providing several design examples and the corresponding Bloch equation simulation results, which include a 2D STA 90° selective excitation pulse and a 2D LCLTA 180° selective inversion pulse. We then demonstrate the effectiveness of optimal control at different k-space acceleration factors using a 2D 180° selective refocusing pulse design example, followed by a study on the peak RF amplitude and total RF energy at different acceleration factors. Finally, we present two sets of experimental parallel transmission results on a phantom to demonstrate the effectiveness of optimal control to optimize RF pulses designed by existing methods: one using a 2D 90° excitation pulse (with a gradient echo pulse sequence) for B1 inhomogeneity correction and the other using both a 2D 90° excitation pulse and a 2D 180° refocusing pulse (with a spin-echo pulse sequence) for reduced field-of-view (FOV) imaging.
THEORY
Spin Systems Under Multichannel and Multidimensional RF Pulses
For on resonance spins, when both an external complex RF pulse B1(t) = B1,x(t) + iB1,y(t) and a gradient field G(t) = [Gx(t), Gy(t), Gz(t)]T for multidimensional spatial selectivity are applied, the Bloch equation without relaxation terms can be written as the following matrix form:
| [1] |
where r = [x, y, z]T is the spatial location vector (which can be 1D or 2D as well), “·” in “G(t) · r” is the inner product operator for vectors, M(r,t) = [Mx(r,t), My(r,t), Mz(r,t)]T is the magnetization vector at location r and time t with x, y, and z components Mx, My, Mz, respectively, γ is the gyromagnetic ratio of the nucleus of interest, and Ṁ(r,t) equals ∂M(r,t)/∂t.
When an array of L transmit coils is used, the total effective B1 field is in general a function of both time and space, due to the superposition of space dependent B1 fields excited by each individual coil:
| [2] |
where sl(r) represents the transmit sensitivity of the lth coil, and denotes the RF pulse waveform to be designed for the lth coil, l = 1,2, …, L. Denoting sl(R)(r) = Re{sl(r)}, sl(I)(r) = Im{sl(r)}, , and , Eq. [2] can be rewritten as:
| [3] |
where
| [4] |
and
| [5] |
Replacing B1,x(t) and B1,y(t) in Eq. [1] with Eqs. [4] and [5] yields:
| [6] |
where
| [7] |
| [8] |
and
| [9] |
Concatenating vectors and matrices in Eq. [6] along different r gives:
| [10] |
where
| [11] |
| [12] |
| [13] |
and
| [14] |
with P equal to the number of voxels in space. Equation [10] describes a bilinear system with multiple controls: A(t), B(l), and C(l) are given, M(t) is the state vector, and ul(t) and vl(t) are the controls to be designed to drive M(t) from an initial state to a desired state. Note the controllability of the MR spin system has been established in Ref. 43.
Optimal Control Formulation
In the following, we formulate the multichannel, multidimensional, complex RF pulse design problem as an optimal control problem. Our goal is to design ul(t) and vl(t) to minimize the error in the resulting magnetization profile for a given pulse duration T. Note other formulations, such as minimizing T are also possible (43) although less commonly used. The design is also subject to a few hardware and SAR constraints, such as average RF power (43), peak B1 (51), maximum gradient amplitude and maximum slew rate (50), and RF waveform jaggedness (45). In general, there are two ways to formulate the RF pulse design problem as an optimal control problem (45): 1) a constrained approach, in which only those RF pulses that satisfy certain bounds of each constraint are considered as candidates, and 2) an unconstrained approach, in which all RF pulse shapes are candidates but are penalized by adding additional terms in the cost functional, and weighting parameters are introduced to balance the various terms in the cost functional and make sure the required constraints are not violated. In this work, we consider the penalized unconstrained approach due to its simplicity and the richness of available optimization algorithms. The constrained optimization approach also warrants investigation, but is not pursued in this work. Our experience shows that the penalized unconstrained approach works very well as long as we choose the weighting parameters appropriately. The optimal RF pulse waveforms and final magnetization profiles are also relatively insensitive to small perturbations of the weighting parameters. For simplicity, we consider only the RF power constraint to illustrate the idea of formulating the multidimensional multichannel RF pulse design problem as an optimal control problem with multiple controls. The maximum gradient amplitude and maximum slew rate constraints are satisfied in the gradient waveform design. The pulse jaggedness term can be included in a way similar to RF power constraint (45). The peak B1 is indirectly limited by the RF power constraint and also checked after the pulse design. Note our formulation is analogous to the “minimum-distance” formulation in Ref. 43, and the following derivation is therefore analogous to Eqs. [4] to [14] in Ref. 43. Mathematically, we minimize a cost functional J over all possible controls:
| [15] |
subject to the Bloch Eq. [10]. In Eq. [15], ϕ(M(T)) is a weighted l2 norm of the error of the final state M(T):
| [16] |
where D is the (vectorized) desired magnetization and W is a diagonal matrix containing weights for different spatial locations to emphasize regions-of-interest (e.g., binary weights to exclude the regions outside the object, and/or heuristically-chosen fractional weights for different regions-of-interest), and F(u1, …, uL, v1, …, vL) is a penalty function on RF power:
| [17] |
where α is a relative weighting parameter to balance the two terms in J.
Optimality Condition
The optimal control problem described by Eq. [15] with equality constraint Eq. [10] can be converted into an unconstrained problem through Lagrange multipliers λ(t):
| [18] |
In Eq. [18], the term inside the integral is the Hamiltonian:
| [19] |
According to calculus of variations (52), the first order necessary condition for achieving a local minimum of Eq. [18] is the Euler-Lagrange equations (52):
| [20] |
| [21] |
and
| [22] |
for l = 1,2, …, L. Replacing H in Eq. [20] with Eq. [19] yields:
| [23] |
Considering the antisymmetric structure of A(t), B(l), and C(l), Eq. [23] can be simplified as:
| [24] |
Note Eq. [24] is similar to the corresponding equation for optimal control adiabatic pulse design (47). Replacing H in Eq. [21] with Eqs. [19] and [17] yields:
| [25] |
and similarly, Eq. [22] yields:
| [26] |
for l = 1,2, …, L. According to calculus of variations (52), the boundary conditions are:
| [27] |
and
| [28] |
where M0 is an initial magnetization vector found by concatenating the initial magnetization vectors at every spatial location. Note the theory developed in this work allows arbitrary direction for M0. For a general weighting matrix W in Eq. [16], Eq. [27] becomes
| [29] |
For W = I, where I is an identity matrix, Eq. [27] allows for a simpler form due to the fact that MT(T)M(T) is constant (43):
| [30] |
Equations [10], [24–26], [28], and [29] (or [30] when W = I) constitute the first order necessary condition for achieving a local minimum of Eq. [18]. In these equations, M(t) and λ(t) are the state variables, and ul(t) and vl(t), l = 1,2, …, L, are the controls to be designed. Since the boundary conditions are given at t = 0 for M(t) and t = T for λ(t), we are faced with a two-point boundary-value problem, which does not have a closed-form solution in general (53). A numerical solution is described in the ensuing section.
Numerical Solution
There are several numerical algorithms to solve the two-point boundary-value problem (53), such as the first-order gradient algorithm, the second-order gradient algorithm, and the conjugate-gradient algorithm. The first-order gradient algorithm is relatively simple for implementation. It is guaranteed to converge and has fast convergence for the early iterations (which contribute to most of the decrease in the cost functional). Our experience shows that the first-order gradient algorithm is sufficient to give significant improvement on magnetization profiles within a reasonable time and we therefore propose it to solve the two-point boundary-value problem in this work. The detailed optimization algorithm is as follows.
Step 1: Initialize ul(0)(t) and vl(0)(t), l = 1,2, …, L, with some solution close enough to the true solution. This involves designing RF pulses using existing methods. Choices of such methods will be described in the Design Procedure section.
Step 2: Given M0, integrate Eq. [10] forward to obtain M(0)(t), for all 0 ≤ t ≤ T. The numerical integration method will be described later in this section.
For k = 0,1,2,3…K, where K is the maximum number of iterations, repeat Steps 3–6 as follows.
Step 3: If (M(k)(T)-D)TW(M(k)(T)-D) is smaller than a given error tolerance ε, which means ul(k)(t) and vl(k)(t), l = 1,2, …, L, have satisfactory performance, then the process stops here. Otherwise, move forward to Step 4.
Step 4: Evaluate λ (k)(T)=W(M(k)(T)-D). Integrate Eq. [24] backward to obtain λ(k)(t), for all 0 ≤ t ≤ T.
Step 5: Update ul(t) and vl(t) for l = 1,2,…,L:
| [31] |
and
| [32] |
where μ is the step size. Although some of the advanced techniques, such as the Armijo (54) rule, can be used to choose μ, we find that a heuristic way to choose μ works well too. We choose a predefined μ and evaluate Eqs. [31] and [32]. If the updated controls produce an increased cost ϕ(M(T)), which means μ is too large and the algorithm is not converging, then μ is halved and Eqs. [31] and [32] are evaluated again. The above process repeats until a decreased cost is found, or the maximum number of trials (also predefined) is reached.
Step 6: Given M0, ul(k+1)(t), and vl(k+1)(t), l = 1,2,…,L, integrate Eq. [10] forward to obtain M(k+1)(t), for all 0 ≤ t ≤ T. Increase k by one and go back to Step 3.
For Steps 2 and 6, as an alternative to numerically solving the differential equations, we can discretize t and solve for M(k)(t) using forward rotation operations in spinor forms (32). We note that recent work also proposed to use a similar idea to accelerate the computation of the forward equation (23). For Step 4, we start from the final state λ(T), and use backward rotation operations (rotate by a negative angle starting from t = T backward to t = 0) in spinor form to calculate λ(t) efficiently.
It should be noted that the above optimization algorithm theoretically achieves only a local minimum of the objective functional. So really we are seeking an improved rather than the ultimate global optimal solution. Our experience and the examples in this work show that, as long as the initial “guess” pulse is properly chosen, the result by optimal control is almost surely very good.
Design Procedure
The proposed optimal control method is a general method. It is capable of designing multichannel, multidimensional, complex pulses with an arbitrary initial magnetization and an arbitrary desired magnetization profile (as long as the norm of the magnetization vector is unity at all spatial locations). Spatial weighting is also included in the proposed framework to reflect preference of error spatial distributions (examples of choosing the weights are given in the Results section). The detailed design procedure is the following.
First, depending on applications (e.g., excitation, refocusing, or inversion), we determine M0 and D, and choose an appropriate T. Second, we choose an appropriate k-space trajectory (1,3) and calculate the corresponding gradient waveforms G(t). For example, we can use an inward spiral for 2D excitation pulses (1), an inherently refocused spiral for 2D refocusing/inversion pulses (3), a fast-kz trajectory for 3D excitation pulses (12), and a concentric trajectory for 3D refocusing/inversion pulses (55). The reason we need the notion of k-space here is that we need STA or LCLTA-based methods to initialize RF pulses in later steps. Note the parameters associated with each trajectory (e.g., number of spiral turns) need to be selected jointly with available maximum gradient amplitude and T. Third, based on sl(r) and G(t), we calculate A(t), B(l), and C(l) according to Eqs. [12]–[14] and [7]–[9]. Fourth, we obtain an initial “guess” of the optimal controls by designing the RF pulses using other noniterative methods, such as STA-based method for excitation pulses (16–18), and LCLTA-based method for refocusing and inversion pulses (30). Fifth, we choose an appropriate αto reflect a balance between magnetization profile fidelity and RF power consumption. We also choose the maximum step size μ, maximum number of iterations, and the error tolerance for the optimization algorithm. Sixth, we apply the first-order gradient algorithm detailed in the Theory section to find the optimal ul(t) and vl(t). Then we check whether the pulse amplitudes are smaller than the maximum amplitude allowed by hardware. If not, we need to either increase T or modify the k-space trajectory (e.g., reduce the number of spiral turns in a 2D spiral trajectory), and repeat the above design procedures. Seventh, we verify the RF pulse waveforms by Bloch simulations or experiments.
RESULTS
Bloch Simulations
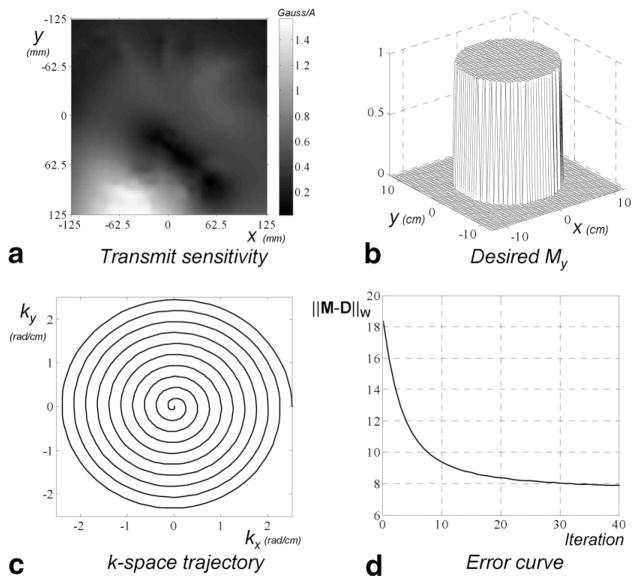
In this section, we present several representative design examples using the proposed method. These examples include a 2D 90° excitation pulse to excite an infinite cylinder, a 2D 180° inversion pulse to invert an infinite cylinder, and some 2D pulses with various acceleration factors. For all the simulations, we use finite-difference time-domain method (FDTD) software to simulate a transmission array of L = 8 equidistant, rectangular loops (1.5 × 16 cm2) placed on a cylindrical coil former (diameter = 30 cm, length = 16 cm) at uniform azimuthal spacing with a 7T main field strength. The numerical coil load equivalent to a head was provided by segmented visible-man data, using appropriate electrical properties for the various tissue types. The original transmit sensitivities have an FOV of 50 × 50 × 100 cm3 (larger than the size of the coil because the electromagnetic field around the coil needs to be modeled to obtain the correct value inside the coil), with a voxel size of 0.5 × 0.5 × 1 cm3. We interpolated the data and reduced the FOV to provide transmission sensitivity maps for various simulations. An example of the transmission sensitivity of one of the channels is shown in Fig. 1a. Bloch equation simulations without relaxation effects are carried out to produce the resulting magnetization profiles. For all the simulations, we use W = I (i.e., treat the excited regions and the side lobes equally) and we normalize the magnetizations by the equilibrium magnetization M0 so that a unity value corresponds to equilibrium M0.
FIG. 1.
2D nonoptimized and optimized 90° excitation pulses. a: Simulated transmission sensitivity of one of the channels. b: Desired My profile. c: k-space trajectory. d: Error reduction curve during the optimization process.
A 2D 90° Excitation Pulse
The first example is to design a 2D 90° excitation pulse to excite an infinite cylinder with a diameter of 20 cm in an FOV of 25 × 25 cm2 (Fig. 1b). The initial magnetization vector pointed in the +z direction at all spatial locations. The matrix size was 50 × 50. We used an inward spiral trajectory without acceleration to cover the k-space (Fig. 1c). The remaining parameters were: number of spiral turns = 10, T = 1.5 ms, number of time samples = 200, time sample duration = 7.5 μs/sample.
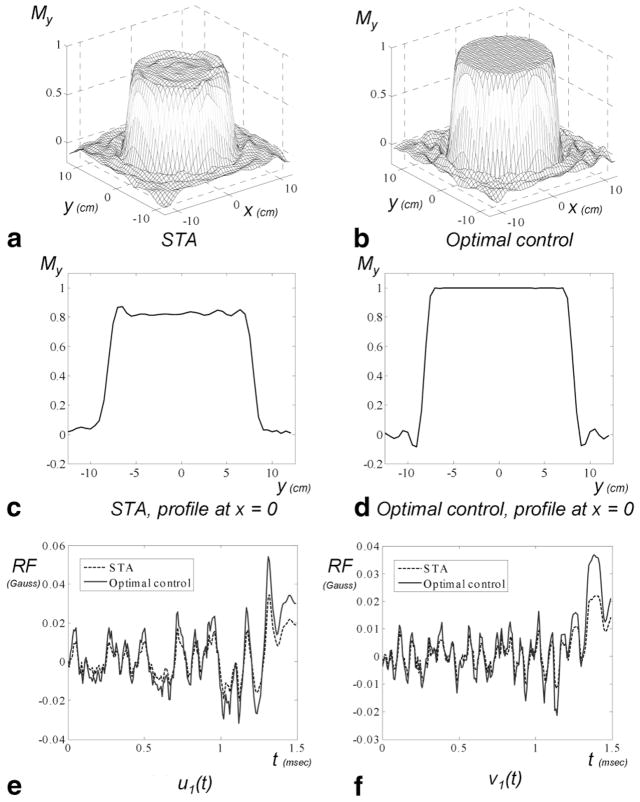
We first used an STA method (18) to design the excitation pulse. As shown in Fig. 2a, after excitation, the My profile not only has considerable ripples on top of the “hat,” which is due to the truncation effect as a result of finite k-space coverage, but also has signal values significantly less than 1 (the targeted value). This is more clearly shown in the 1D profile in Fig. 2c. Using the STA-based pulse as the initial “guess,” we applied the proposed method to optimize the pulse waveforms. The difference between the final magnetization profile and the ideal profile was progressively decreasing (Fig. 1d). After 40 iterations, the resulting optimized pulse generated a significantly improved profile, as shown in Fig. 2b. Compared to Fig. 2a, Fig. 2b has a much flatter hat “top,” and the value on the top is very close to one. This is more clearly shown in Fig. 2d. The real and imaginary parts of the RF pulse of one of the channels are shown in Fig. 2e and f, respectively, for both STA and the optimal control solution. These figures show that the optimal control preserves the main shape of the STA solution, but makes localized modifications of the waveform to compensate for the nonlinearity of Bloch equations, thereby improving the final magnetization profile.
FIG. 2.
Following Fig. 1. a: The My component produced by the STA pulse. b: The My component produced by the optimized pulse. c: 1D profile of (a) at x = 0. d: 1D profile of (b) at x = 0. e: Real components of the STA and optimized pulses of one of the channels. f: Imaginary components of the STA and optimized pulses of one of the channels.
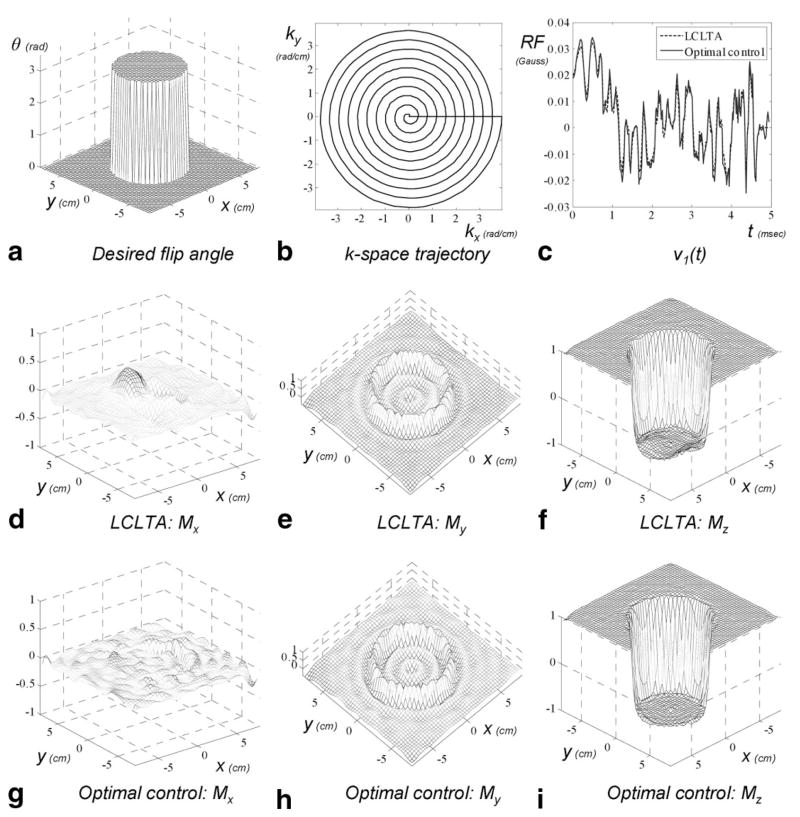
A 2D 180° Inversion Pulse
In this section, we show a design example of a 2D 180° inversion pulse to invert an infinite cylinder with a diameter of 8 cm in an FOV of 16 × 16 cm2 (Fig. 3a). The initial magnetization vector pointed in the +z direction at all spatial locations. Since this is a 180° pulse, the STA method cannot be used to provide a reasonable solution. We used the multichannel multidimensional LCLTA method (30) to design the initial pulse. We adopted an inherently refocused spiral trajectory (3) for k-space coverage (Fig. 3b). The remaining parameters were: number of spiral turns = 10, T = 5 ms, and number of time points = 200. As shown in Fig. 3d–f, although Mx stays close to zero at most spatial locations, some initial magnetization indeed gets flipped to Mx, resulting in large errors in the final Mx profile; My is kept to close to zero very well except near the edge of the cylinder, which is inevitable due to the finite k-space coverage; Mz is inverted inside the cylinder, but some distortion due to the nonlinearity of Bloch equation is noticeable. These errors were well corrected by the optimal control method, as shown in Fig. 3g–i: the Mx and Mz components have much higher fidelity than those from the LCLTA solution, while My has similar performance to that from the LCLTA solution. The LCLTA and the optimal control pulses of one of the channels are shown in Fig. 3c. Again, the optimal control method made slight modifications to the LCLTA solution to produce a significantly improved profile.
FIG. 3.
2D nonoptimized and optimized 180° inversion pulses. a: Desired flip angle profile. b: k-Space trajectory. c: Imaginary part of the pulses (one of the channels) designed by the LCLTA method and by the proposed method. d–f: Mx, My, and Mz components of magnetization profile produced by the LCLTA method. g–i: Mx, My, and Mz components of magnetization profile produced by the proposed method.
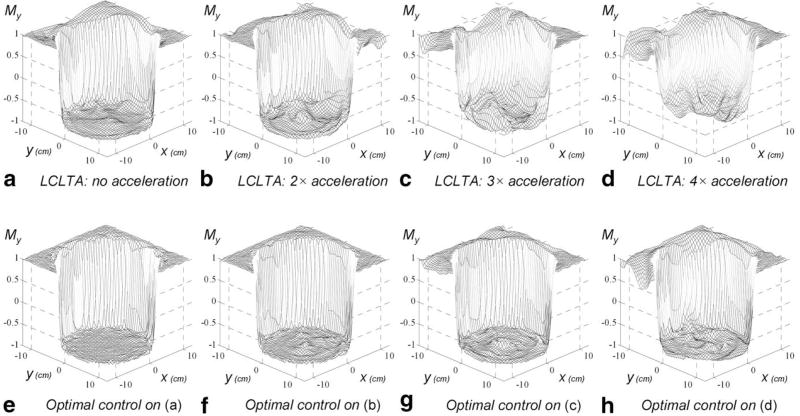
2D 180° Refocusing Pulses With Various Acceleration Factors
We applied the proposed optimization algorithm to 2D 180° refocusing pulses with various acceleration factors using LCLTA pulses as the initial guess. In this simulation (and the spin-echo experiment in a later section), the initial magnetization was assumed to point in the +y direction (the ideal case). The desired magnetization vector after applying the refocusing pulse pointed in the −y direction inside an infinite cylinder with a diameter of 20 cm, and +y direction outside the cylinder. Note the optimal control formulation based on the above assumption on initial magnetization does not guarantee the performance of the resulting refocusing pulses when the initial magnetization profile significantly deviates from the ideal profile (i.e., initial magnetization vector has strong x component). While designing refocusing pulses that are robust to nonideal initial magnetization profile is beyond the scope of this work, it is worth pointing out that such robust refocusing pulses can be designed by slightly modifying the proposed algorithm to include two optimal control processes, one starting with initial magnetization pointing in +y and ending with magnetization pointing in −y, and the other starting with +x and ending with +x as well (43). The FOV used in the simulation was 25 × 25 cm2. Inherently refocused spiral trajectories with reduction factors R = 1, 2, 3, 4 were used for k-space coverage. The pulse duration was T = 5/R ms, with the number of spiral turns given by 12/R (because the distance between two consecutive turns was proportional to R). The My components from LCLTA pulses are shown in Fig. 4a–d. These figures show that the error of the final magnetization profile increases as R increases. With eight transmit coils, a small acceleration factor (e.g., 2) produces results with tolerable degradation, while a large acceleration factor (e.g., 3 and 4 in this example) produces large errors. The optimal control method is able to improve profiles at all acceleration factors. This is shown as a much flatter “bottom” of the cylinder and much smaller ripples outside the cylinder. More importantly, it reduces the large magnetization profile errors produced by LCLTA pulses at 3× and 4× accelerations to well-tolerable levels. This implies that with optimal control, we can achieve larger accelerations than existing methods, thereby reducing the total pulse duration significantly. These results show great potential in accelerating long RF pulses, such as those in 3D selective applications.
FIG. 4.
2D selective 180° refocusing pulses with various acceleration factors. a–d: The My components produced by LCLTA pulses with R = 1,2,3,4, respectively. e–h: The My components produced by the corresponding optimized pulses.
A comparison of the refocusing pulses in Fig. 4 with respect to peak RF amplitude and total RF energy is given in Table 1. As R increases, both peak RF amplitude and total RF energy increase for both LCLTA and optimized pulses (with a slight exception at R = 3 and R = 4 for LCLTA pulses). The increase is approximately proportional to R. At small R (e.g., R = 1, 2), optimal control pulses have similar peak RF amplitude and total RF energy to those of LCLTA pulses. This is because slight modification at small R is sufficient to produce a good magnetization profile. There is even a slight decrease of peak RF amplitude at R = 1 and R = 2, which means in this example, that optimal control happens to reduce some of the high peaks in the LCLTA pulses. At large R (e.g., R = 3, 4), optimized pulses have a significant increase of peak RF amplitude and total RF energy over the LCLTA pulses. This is because for such cases, large modification of pulses is needed, and the majority of the modification is to increase the RF amplitude to bring the tip angle from smaller than 180° to 180°.
Table 1.
Comparison of 2D Selective 180° Refocusing Pulses With Different Acceleration Factors in Fig. 4
| Acceleration | Peak RF amplitude (Gauss) |
Total RF energy (10−5 · Gauss2 · ms) |
||
|---|---|---|---|---|
| LCLTA | Optimized | LCLTA | Optimized | |
| R = 1 | 0.16 | 0.15 | 4.6 | 5.5 |
| R = 2 | 0.29 | 0.28 | 7.7 | 10 |
| R = 3 | 0.40 | 0.47 | 10 | 17 |
| R = 4 | 0.55 | 0.74 | 9.9 | 21 |
2D 90° Excitation Pulses With 2× Acceleration vs. Half k-Space Coverage
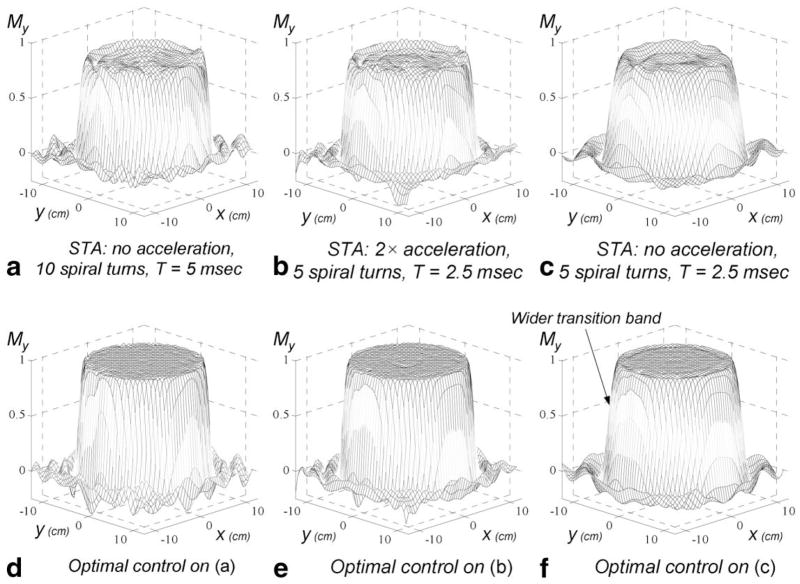
In Fig. 5, we compare 2D 90° excitation pulses (with and without optimization) whose pulse duration is reduced in different ways. The initial magnetization vector pointed in the +z direction at all spatial locations. The ideal magnetization vector after applying the RF pulse pointed in the +y direction inside an infinite cylinder with a diameter of 20 cm, and stayed in the +z direction outside. The FOV was 25 × 25 cm2. An inward spiral trajectory was used for k-space coverage. Figure 5a shows the My component from a 5 ms STA pulse with 10 spiral turns. In Fig. 5b and c, two ways to achieve T = 2.5 ms are compared. For Fig. 5b, we undersampled k-space by two while keeping the same k-space coverage (five spiral turns), while for Fig. 5c, we did not undersample k-space but reduced k-space coverage by a factor of 2 (used the first five spiral turns). Both Fig. 5b and c have some ripples on top of the “hat.” Figure 5b appears similar to Fig. 5a because parallel transmission with eight channels is able to correct the effect due to undersampling when R is small. Figure 5c has wider transition band than Fig. 5a and b because of the reduced k-space coverage. With optimal control, profiles from all three pulses were improved. The My component from the pulse with 2× undersampling (Fig. 5e) is almost the same as that from the pulse without undersampling (Fig. 5d). The My component from the pulse with less k-space coverage (Fig. 5f) also has very flat top of the “hat,” but the transition band is still wider than Fig. 5d and e. These results imply that the optimal control method is quite effective at correcting for ripple-like errors, but may not be as effective for edge-like errors (such as a wide transition band). In this sense, undersampling with small acceleration factors is preferred over less k-space coverage when using the optimal control method. However, it should be also noted that 2× undersampling almost doubles the peak RF amplitude and total RF energy, while less k-space coverage with no acceleration almost preserves these parameters, as detailed in Table 2.
FIG. 5.
2D selective 90° excitation pulses comparing two-fold acceleration and half k-space coverage (two-fold reduction in resolution). a: The My component produced by a 5-ms-long STA pulse. The spiral trajectory to obtain the STA pulse for (a) is (b) undersampled by two or (c) modified to cover only half as much the k-space to achieve 2.5-ms-long pulses for the same excitation profile. The proposed method is applied and the results are shown in (d–f), which correspond to (a–c). These figures show that for parallel transmission using the optimal control pulses, trajectories with a small R are preferred over trajectories with reduced k-space coverage.
Table 2.
Comparison of 2D Selective 90° Excitation Pulses With 2× Acceleration and Half k-Space Coverage in Fig. 5
| Trajectories | Peak RF amplitude (10−2 Gauss) |
Total RF energy (10−6 · Gauss2 · ms) |
||
|---|---|---|---|---|
| STA | Optimized | STA | Optimized | |
| 1) R = 1, 10 spiral turns | 2.6 | 3.9 | 1.4 | 3.1 |
| 2) R = 2, same k-space coverage as 1) | 4.2 | 6.8 | 2.4 | 5.5 |
| 3) R = 1, half k-space coverage of 1) | 2.6 | 3.9 | 1.4 | 3.0 |
Experiments
We conducted experiments on a 1.5T GE Signa scanner (GE Healthcare, Milwaukee, WI, USA) with parallel transmission capability (19) to further validate the effectiveness of the optimal control method. The eight-channel parallel transmission system was built by integrating four sets of GE Healthcare Excite II system electronics (each containing two exciter boards). An eight-channel transmit-only head-coil array (19) was used to transmit RF pulses. This array has a cylindrical structure where each element (18 × 6 cm2) is distributed azimuthally on a coil former with a diameter of 27 cm. A single-channel quadrature body coil was used to receive signals. A uniform circular slab phantom with a diameter of 24 cm was used to test 2D spatially selective pulses. In the following, we show two experimental results: one using a 2D 90° excitation pulse (with a gradient echo sequence) for B1 inhomogeneity correction and the other using both a 2D 90° excitation pulse and a 2D 180° refocusing pulse (with a spin-echo sequence) for reduced FOV imaging.
2D Gradient Echo Imaging for B1 Inhomogeneity Correction
The purpose of this study is to compare nonoptimized and optimized 2D 90° excitation pulses in terms of B1 inhomogeneity correction. A modified gradient echo pulse sequence was used and the target magnetization profile was a cylinder with a diameter of 20 cm (slightly smaller than the phantom). We covered the k-space with a six-turn inward spiral trajectory with two-fold acceleration along the radial direction (Fig. 6a). This trajectory was implemented using gradient waveforms shown in Fig. 6b. The slew rate constraint in the design of the inward spiral was 14500 Gauss/cm/s (the hardware limit). We used a method described in Ref. 19 for excitation B1 map calibration. The B1 map for each element was calibrated separately, each requiring an imaging experiment that uses a single element of the coil array for transmission with zero inputs to other elements and the body coil for reception. The matrix size for the B1 map acquisition was 64 × 64 and the B1 map of one of the channels is shown in Fig. 6c. An STA-based method (18) was used to design the 2.1 ms excitation pulse, which was then optimized by the proposed method. Magnitudes of the STA and optimal control pulses of one of the channels are shown in Fig. 6d. The remaining parameters were: FOV = 30 × 30 cm2, TE = 15 ms, TR = 80 ms, matrix size = 256 × 256 for signal reception.
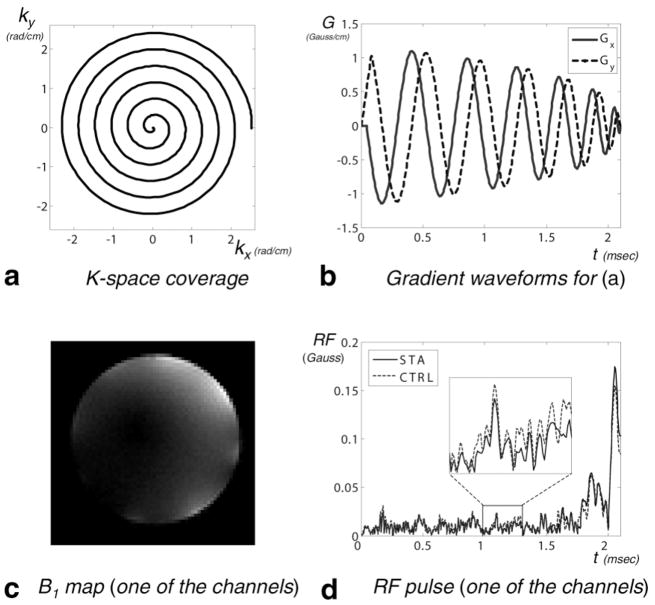
FIG. 6.
Parallel transmission experiment using a gradient echo sequence for B1 inhomogeneity correction. a: A six-turn inward spiral trajectory with two-fold acceleration along the radial direction to cover the k-space. b: Gradient waveforms to implement (a), with slew rate constraint of 14,500 Gauss/cm/s. c: Magnitude of the B1 map of one of the channels. d: The STA and optimal control (labeled as CTRL) 90° excitation pulses of one of the channels.
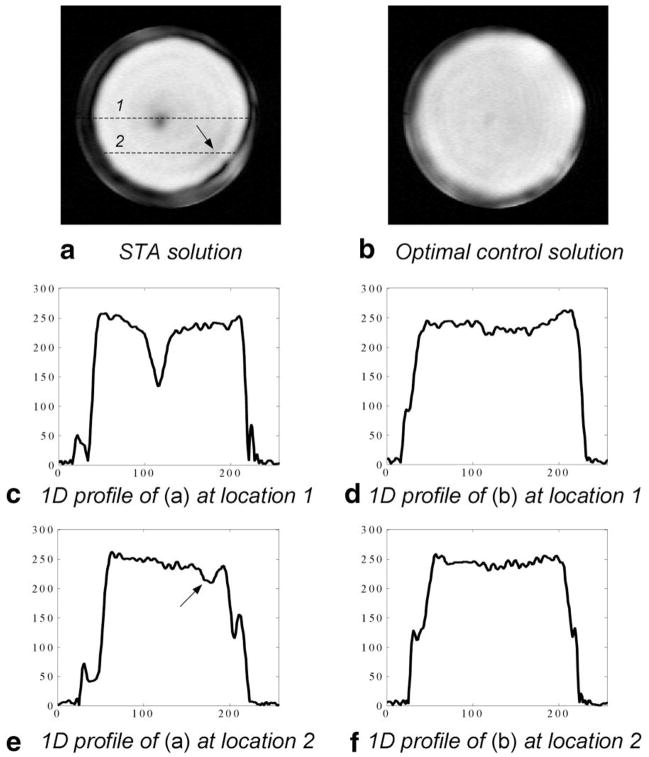
The images acquired by STA and optimal control pulses are compared in Fig. 7a and b. There is a dark area in the center of the STA image (also observed in the Bloch simulation result using the STA pulse), possibly due to a phase cancellation of magnetization from individual channels. This problem is well solved in the optimal control image where we have used weight 1 for the dark area in the center, weight 0.3 for the rest of the object, and weight 0 for the area outside the object. There are also some noticeable ripples in the STA image (marked by the arrow in Fig. 7a) due to the nonlinearity of Bloch equation and finite sampling of the k-space. These ripples are significantly suppressed in the optimal control image. The optimal control image (mean = 241, SD = 7.9, maximum difference of intensity = 60) is more homogeneous than the STA image (mean = 242, SD = 15.3, maximum difference of intensity = 147) in the region of interest. Two 1D profiles at different y locations are also plotted in Fig. 7c–f to reveal details. Note that for location 1, the sharp drop of signal intensity at the center of STA profile (Fig. 7c) does not show in the optimal control profile (Fig. 7d); for location 2, the signal intensity decrease along the x-axis as well as the signal ripple (marked by the arrow in Fig. 7e) also does not show in the optimal control profile (Fig. 7f). This result suggests that optimal control can help achieve more homogeneous excitation, which is essential for high field (e.g., 7T) imaging (56). This is a subject of ongoing research.
FIG. 7.
Images of the gradient echo imaging experiment in Fig. 6. a: Image from the STA pulse. There is a dark area in the center and some noticeable ripples (marked by the arrow). b: Image from the optimized pulse. The image is more homogeneous than (a). c,d: Comparison of 1D profiles from both solutions at Location 1. e,f: Comparison of 1D profiles at Location 2.
2D Spin-Echo Imaging for Reduced FOV Imaging
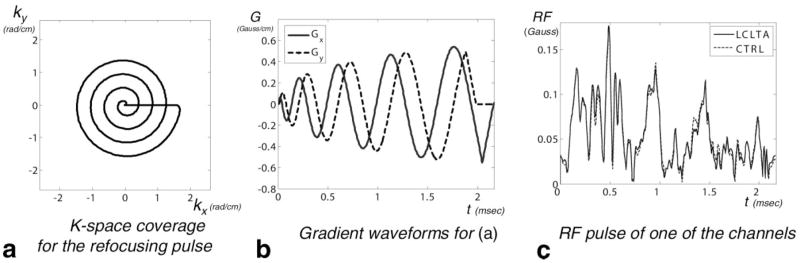
The motivation of this experiment is to compare the performance of the nonoptimized and optimized 180° pulses in the reduced FOV application using a modified spin-echo sequence. The same phantom and B1 mapping method as for the previous experiment were used. The 2D target profile was an off-centered cylinder with a diameter of 6 cm. To achieve this profile, we designed a 2D 90° excitation pulse using the STA method (18) to excite only the spins inside the 6-cm cylinder and a 2D 180° refocusing pulse using the LCLTA method (30) to refocus only the magnetization inside the cylinder. For the 90° excitation pulse, the same gradient waveform as in Fig. 6b was used. For the 180° refocusing pulse, we used a four-turn inherently refocused outward spiral trajectory with two-fold acceleration along the radial direction to cover the k-space (Fig. 8a). See the corresponding gradient waveforms in Fig. 8b. Note that in order to reduce the peak amplitude of the refocusing pulses, we reduced the gradient amplitude by imposing a slew rate constraint of 5000 Gauss/cm/s in the design of the outward spiral. Both the excitation and refocusing pulses were optimized using the proposed method with binary weights to mask out the areas outside the phantom. The optimized and nonoptimized 180° refocusing pulses of one of the channels is shown in Fig. 8c. The remaining parameters were: FOV = 30 × 30 cm2, TE = 15 ms, and TR = 100 ms.
FIG. 8.
Parallel transmission experiment with nonoptimized and optimized pulses using a spin-echo sequence for reduced FOV imaging. a: A four-turn inherently refocused outward spiral trajectory with two-fold acceleration along the radial direction to cover k-space for the refocusing pulse. The spiral trajectory for the excitation k-space is the same as that in Fig. 6a. b: The gradient waveform to implement (a), where we reduced the gradient amplitude by imposing a slew rate constraint of 5000 Gauss/cm/s to reduce the peak amplitude of the refocusing pulse. c: The LCLTA and optimal control 180° refocusing pulses of one of the channels.
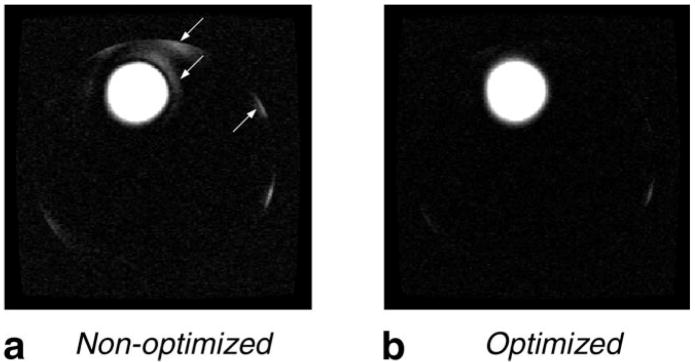
The spin-echo image from the nonoptimized pulses (STA 90° + LCLTA 180°) in Fig. 9a shows quite good spatial selectivity. However, there are some significant artifacts near the prescribed cylindrical region and near the edge of the phantom, as marked by the arrows in Fig. 9a. These artifacts are primarily due to the nonlinearity of the Bloch equation and limited k-space coverage. As shown in Fig. 9b, the image from the optimized pulses (optimized 90° + optimized 180°) shows a very clean “background” outside of the prescribed region. This result implies that the optimal control method can help reduce signal leakage in reduced FOV imaging.
FIG. 9.
Spin-echo images from the experiment in Fig. 8. a: Image using nonoptimized pulses (STA 90° + LCLTA 180°). There were some significant artifacts as marked by the arrows. These artifacts are primarily due to the nonlinearity of Bloch equation and limited k-space coverage. b: Image using optimized pulses (optimized 90° + optimized180°). This image has a very clean “background” outside of the prescribed region.
DISCUSSION
The optimal control method optimizes parallel transmission pulses designed by existing methods (e.g., the STA and the LCLTA methods). The fine tuning of the pulse waveforms enabled by optimal control compensates for the nonlinearity of the Bloch equation and limited k-space coverage, thereby improving the quality of the resulting magnetization profile. It is a very general method in the sense that it can optimize pulses to drive magnetization between any valid initial and terminal magnetization profiles. This generality allows the optimal control method to cover the wide spectrum of excitation, refocusing, and inversion pulses, which can lead to potential applications such as accurate large-tip-angle gradient echo imaging, multidimensional spin-echo imaging, and multidimensional inversion-recovery imaging for parallel transmission. For the proposed first order gradient optimization algorithm, the value of the cost functional always decreases monotonically with increased iterations. Therefore there is a simple tradeoff between magnetization profile error and computation time (i.e., smaller error requires more iterations to optimize the RF pulse). The proposed framework also allows easy inclusion of other constraints (when necessary), such as constraints on gradient amplitude, RF pulse amplitude, and RF waveform jaggedness.
The proposed implementation of the optimal control algorithm is an iterative method. Although the computational complexity is significantly reduced by using rotation operations in spinor forms to solve for Eqs. [10] and [24], the optimization algorithm can still be time consuming. For example, using MATLAB (Mathworks, Natick, MA, USA) on a PC with a 1.66-GHz Intel Pentium 4 Core and 1 GB RAM, typical optimization for 2D pulses can take as long as 1–5 min, while optimization for 3D pulses can take more than 10 min. The actual time depends on the parameters, such as resolution, step size, initial solution, and error tolerance. We note that acceleration of the proposed algorithm is expected with advanced computers and optimized code. The algorithm finds the local minimum of the cost functional. So the optimized pulses are dependent on the initial solutions and theoretically can be quite suboptimal. However, our experience shows that as long as the initial pulse is appropriately designed (e.g., using the STA method for excitation pulses, and using the LCLTA method for refocusing and inversion pulses), the optimal control method typically gives pulses that produce high quality magnetization profiles. The off-resonance effects are not discussed in this work, but it should be fairly straightforward to include an off-resonance term in the optimal control framework and a similar design procedure should apply.
CONCLUSIONS
In this work, we formulate the multidimensional multichannel RF pulse design as an optimal control problem with multiple controls based directly on the Bloch equation, which generates pulses producing improved spatial selectivity or homogeneity in the resulting magnetization profiles. We derive the necessary conditions for the optimal solution using calculus of variations, propose to use a first-order gradient optimization algorithm to iteratively solve the optimal control problem, and present a systematic design procedure. Bloch simulation results using various design examples and two parallel transmission experiments show that optimized pulses generally lead to significantly better magnetization profiles than nonoptimized pulses, especially when the k-space acceleration factor is relatively large. The proposed method holds great potential in applications involving reduced FOV imaging and B1 inhomogeneity correction, especially those in high field.
Acknowledgments
National Institute of Health (NIH); grant number: R01 EB005307.
References
- 1.Pauly J, Nishimura D, Macovski A. A k-space analysis of small-tip-angle excitation. J Magn Reson. 1989;81:43–56. doi: 10.1016/j.jmr.2011.09.023. [DOI] [PubMed] [Google Scholar]
- 2.Hardy CJ, Cline HE. Spatial localization in two dimensions using NMR designer pulses. J Magn Reson. 1989;82:647–654. [Google Scholar]
- 3.Pauly J, Nishimura D, Macovski A. A linear class of large-tip-angle selective excitation pulses. J Magn Reson. 1989;82:571–587. [Google Scholar]
- 4.Hardy CJ, Cline HE. Broadband nuclear magnetic resonance pulses with two-dimensional spatial selectivity. J Appl Phys. 1989;66:1513–1516. [Google Scholar]
- 5.Bottomley PA, Hardy CJ. Two-dimensional spatially selective spin inversion and spin-echo refocusing with a single nuclear magnetic resonance pulse. J Appl Phys. 1987;62:4284–4290. [Google Scholar]
- 6.Pauly J, Spielman D, Macovski A. Echo-planar spin-echo and inversion pulses. Magn Reson Med. 1993;29:776–782. doi: 10.1002/mrm.1910290609. [DOI] [PubMed] [Google Scholar]
- 7.Pauly JM, Hu BS, Wang SJ, Nishimura DG, Macovski A. A three-dimensional spin-echo or inversion pulse. Magn Reson Med. 1993;29:2–6. doi: 10.1002/mrm.1910290103. [DOI] [PubMed] [Google Scholar]
- 8.Schröder C, Börnert P, Aldefeld B. Spatial excitation using variable-density spiral trajectories. J Magn Reson Imag. 2003;18:136–141. doi: 10.1002/jmri.10334. [DOI] [PubMed] [Google Scholar]
- 9.Börnert P, Schäffter T. Curved slice imaging. Magn Reson Med. 1996;36:932–939. doi: 10.1002/mrm.1910360616. [DOI] [PubMed] [Google Scholar]
- 10.Meyer CH, Pauly JM, Macovski A, Nishimura DG. Simultaneous spatial and spectral selective excitation. Magn Reson Med. 1990;15:287–304. doi: 10.1002/mrm.1910150211. [DOI] [PubMed] [Google Scholar]
- 11.Deichmann R, Good CD, Turner R. RF inhomogeneity compensation in structural brain imaging. Magn Reson Med. 2002;47:398 – 402. doi: 10.1002/mrm.10050. [DOI] [PubMed] [Google Scholar]
- 12.Saekho S, Yip C, Noll DC, Boada FE, Stenger VA. Fast-kz three-dimensional tailored radiofrequency pulse for reduced B1 inhomogeneity. Magn Reson Med. 2006;55:719–724. doi: 10.1002/mrm.20840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Stenger VA, Boada FE, Noll DC. Three-dimensional tailored RF pulses for the reduction of susceptibility artifacts in T2*-weighted functional MRI. Magn Reson Med. 2000;44:525–531. doi: 10.1002/1522-2594(200010)44:4<525::aid-mrm5>3.0.co;2-l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Stenger VA, Boada FE, Noll DC. Variable-density spiral 3D tailored RF pulses. Magn Reson Med. 2003;50:1100–1106. doi: 10.1002/mrm.10623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nehrke K, Börnert P, Groen J, Smink J, Böck JC. On the performance and accuracy of 2D navigator pulses. Magn Reson Imag. 1999;17:1173–1181. doi: 10.1016/s0730-725x(99)00043-0. [DOI] [PubMed] [Google Scholar]
- 16.Katscher U, Börnert P, Leussler C, van den Brink JS. Transmit SENSE. Magn Reson Med. 2003;49:144–150. doi: 10.1002/mrm.10353. [DOI] [PubMed] [Google Scholar]
- 17.Zhu Y. Parallel excitation with an array of transmit coils. Magn Reson Med. 2004;51:775–784. doi: 10.1002/mrm.20011. [DOI] [PubMed] [Google Scholar]
- 18.Grissom WA, Yip C, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn Reson Med. 2006;56:620 – 629. doi: 10.1002/mrm.20978. [DOI] [PubMed] [Google Scholar]
- 19.Zhu Y, Watkins R, Giaquinto R, Hardy C, Kenwood G, Mathias S, Valent T, Denzin M, Hopkins J, Peterson W, Mock B. Parallel excitation on an eight transmit-channel MRI system. Proceedings of the 13th Annual Meeting of ISMRM; Miami Beach, FL, USA. 2005. (Abstract 14) [Google Scholar]
- 20.Ullmann P, Junge S, Wick M, Ruhm W, Hennig J. Experimental analysis of parallel excitation using dedicated coil setups and simultaneous RF transmission on multiple channels. Magn Reson Med. 2005;54:994–1001. doi: 10.1002/mrm.20646. [DOI] [PubMed] [Google Scholar]
- 21.Katscher U, Börnert P. Parallel RF transmission in MRI. NMR Biomed. 2006;19:393–400. doi: 10.1002/nbm.1049. [DOI] [PubMed] [Google Scholar]
- 22.Zhang Z, Stenger VA. Validation of transmit SENSE with reciprocity. Proceedings of the 13th Annual Meeting of ISMRM, Miami Beach; Florida, USA. 2005. (Abstract 2434) [Google Scholar]
- 23.Ulloa JL, Callaghan M, Guarini M, Hajnal JV, Irarrazaval P. Calculation of B1 pulses for RF shimming at arbitrary flip angle using multiple transmitters. Proceedings of the 14th Annual Meeting of ISMRM; Seattle, WA, USA. 2006. (Abstract 3016) [Google Scholar]
- 24.Zhang Z, Yip C, Grissom WA, Boada FE, Noll DC, Stenger VA. Reduction of B1 inhomogeneity using transmit SENSE slice-select pulses. Proceedings of the 14th Annual Meeting of ISMRM; Seattle, WA, USA. 2006. (Abstract 602) [Google Scholar]
- 25.Griswold MA, Kannengiesser S, Müller M, Jakob PM. Autocalibrated accelerated parallel excitation (transmit-GRAPPA). Proceedings of the 13th Annual Meeting of ISMRM; Miami Beach, Florida, USA. 2005. (Abstract 2435) [Google Scholar]
- 26.Katscher U, Vernickel P, Hanft M. Static and dynamic RF-shimming in the framework of transmit SENSE. Proceedings of the 13th Annual Meeting of ISMRM; Miami Beach, Florida, USA. 2005. (Abstract 2256) [Google Scholar]
- 27.Graesslin I, Niemann M, Harvey P, Vernickel P. SAR and RF power reduction with parallel excitation using non-Cartesian trajectories. MAGMA. 2005;18:S251. [Google Scholar]
- 28.Zhu Y. RF power deposition and “g-factor” in parallel transmit. Proceedings of the 14th Annual Meeting of ISMRM; Seattle, WA, USA. 2006. (Abstract 599) [Google Scholar]
- 29.Katscher U, Börnert P, van den Brink JS. Theoretical and numerical aspects of transmit SENSE. IEEE Trans Med Imaging. 2004;23:520–525. doi: 10.1109/TMI.2004.824151. [DOI] [PubMed] [Google Scholar]
- 30.Xu D, King KF, Zhu Y, McKinnon GC, Liang ZP. A noniterative method to design large-tip-angle multidimensional spatially-selective radio frequency pulses for parallel transmission. Magn Reson Med. 2007;58:326–334. doi: 10.1002/mrm.21314. [DOI] [PubMed] [Google Scholar]
- 31.Hoult DI. The solution of the Bloch equations in the presence of a varying B1 field—an approach to selective pulse analysis. J Magn Reson. 1979;35:69 – 86. [Google Scholar]
- 32.Pauly J, Roux PL, Nishimura D, Macovski A. Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm. IEEE Trans Med Imaging. 1991;10:53–65. doi: 10.1109/42.75611. [DOI] [PubMed] [Google Scholar]
- 33.Barratt C, Fackerell ED, Rosenfeld D. The application of spinors to solving the Bloch equations. J Magn Reson. 1989;85:35–41. doi: 10.1103/physreva.40.3429. [DOI] [PubMed] [Google Scholar]
- 34.Gezelter JD, Freeman R. Use of neural networks to design shaped radiofrequency pulses. J Magn Reson. 1990;90:397– 404. [Google Scholar]
- 35.Wu XL, Freeman R. Darwin’s ideas applied to magnetic resonance. The marriage broker J Magn Reson. 1989;85:414 – 420. [Google Scholar]
- 36.Geen H, Wimperis S, Freeman R. Band-selective pulses without phase distortion. A simulated annealing approach. J Magn Reson. 1989;85:620 – 627. [Google Scholar]
- 37.Carlson JW. A calculational technique for custom tailoring of RF pulses in selective excitation magnetic resonance experiments. J Magn Reson. 1986;67:551–555. [Google Scholar]
- 38.Lebsack ET, Wright SM. Iterative RF pulse refinement for magnetic resonance imaging. IEEE Trans Biomed Eng. 2002;49:41– 48. doi: 10.1109/10.972838. [DOI] [PubMed] [Google Scholar]
- 39.Ngo JT, Morris PG. General solution to the NMR excitation problem for noninteracting spins. Magn Reson Med. 1987;5:217–237. doi: 10.1002/mrm.1910050303. [DOI] [PubMed] [Google Scholar]
- 40.Rourke DE, Morris PG. The inverse scattering transform and its use in the exact inversion of the Bloch equation for noninteracting spins. J Magn Reson. 1992;99:118 –138. [Google Scholar]
- 41.Buonocore MH. RF pulse design using the inverse scattering transform. Magn Reson Med. 1993;29:470 – 477. doi: 10.1002/mrm.1910290408. [DOI] [PubMed] [Google Scholar]
- 42.Rourke D, Prior MJW, Morris PG, Lohman JAB. Stereographic projection method of exactly calculating selective pulses. J Magn Reson A. 1994;107:203–214. [Google Scholar]
- 43.Conolly S, Nishimura D, Macovski A. Optimal control solutions to the magnetic resonance selective excitation problem. IEEE Trans Med Imaging. 1986;MI-5:106–115. doi: 10.1109/TMI.1986.4307754. [DOI] [PubMed] [Google Scholar]
- 44.Mao J, Mareci TH, Scott KN, Andrew ER. Selective inversion radiofrequency pulses by optimal control. J Magn Reson. 1986;70:310 –318. [Google Scholar]
- 45.Murdoch JB, Lent AH, Kritzer MR. Computer-optimized narrowband pulses for multislice imaging. J Magn Reson. 1987;74:226 –263. [Google Scholar]
- 46.Conolly S, Nishimura D, Macovski A. Selective complex pulse design by optimal control theory. Proceedings of the 5th Annual Meeting of SMRM; Montreal, Canada. 1986. pp. 1456–1457. [Google Scholar]
- 47.Rosenfeld D, Zur Y. Design of adiabatic selective pulses using optimal control theory. Magn Reson Med. 1996;36:401– 409. doi: 10.1002/mrm.1910360311. [DOI] [PubMed] [Google Scholar]
- 48.Skinner TE, Reiss TO, Luy B, Khaneja N, Glaser SJ. Application of optimal control theory to the design of broadband excitation pulses for high-resolution NMR. J Magn Reson. 2003;163:8 –15. doi: 10.1016/s1090-7807(03)00153-8. [DOI] [PubMed] [Google Scholar]
- 49.Ulloa JL, Guarini M, Guesalaga A, Irarrazaval P. Chebyshev series for designing RF pulses employing an optimal control approach. IEEE Trans Med Imaging. 2004;23:1445–1452. doi: 10.1109/TMI.2004.835602. [DOI] [PubMed] [Google Scholar]
- 50.Anand CK, Stoyan SJ, Terlaky T. Advanced Optimization Laboratory. Hamilton, Ontario, Canada: McMaster University; 2005. Optimizing the gVERSE RF pulse design via optimal control. Technical report. [Google Scholar]
- 51.Yip CY, Fessler JA, Noll DC. Iterative RF pulse design for multidimensional, small-tip-angle selective excitation. Magn Reson Med. 2005;54:908 –917. doi: 10.1002/mrm.20631. [DOI] [PubMed] [Google Scholar]
- 52.Gelfand IM, Fomin SV. Calculus of variations. New York: Dover Publications; 2000. [Google Scholar]
- 53.Bryson AE, Ho YC. Applied optimal control. Washington, DC: Hemisphere Republishing Corporation; 1975. [Google Scholar]
- 54.Armijo L. Minimization of function having Lipschitz continuous first partial derivatives. Pacific J Math. 1966;16:1–13. [Google Scholar]
- 55.Xu D, King KF, McKinnon GC, Liang ZP. Reducing B1 inhomogeneity using optimized parallel transmit pulses. Proceedings of the 15th Annual Meeting of ISMRM; Berlin, Germany. 2007. (Abstract 1700) [Google Scholar]
- 56.Vaughan JT, Garwood M, Collins CM, Liu W, DelaBarre L, Adriany G, Andersen P, Merkle H, Goebel R, Smith MB, Ugurbil K. 7T vs. 4T: RF power, homogeneity, and signal-to-noise comparison in head images. Magn Reson Med. 2001;46:24 –30. doi: 10.1002/mrm.1156. [DOI] [PubMed] [Google Scholar]