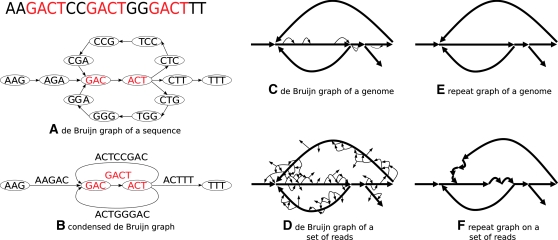
Figure 2.

From de Bruijn graphs to repeat graphs. The de Bruijn graph of a sequence contains a vertex for every k-mer in the sequence, and an edge (u, v) for every pair of consecutive (overlapping) k-mers in the sequence (A). The condensed de Bruijn graph replaces all paths containing nonbranching vertices by a single edge labeled by the sequence that generated the path (B). When the condensed de Bruijn graph is constructed on a genome, it contains some small bulges and whirls representing repeats with slightly varying repeat copies (C). In the repeat graph, the bulges and whirls are removed (E). The de Bruijn graph of reads contains additional spurious bulges and whirls caused by sequencing errors in reads (D). The goal of the Eulerian assembly is to construct the repeat graph of reads (F) that approximates the repeat graph of the genome. Different studies use different terminology, e.g., the edges of these graphs are referred to as “blocks” in Zerbino and Birney (2008) and “unipaths” in Butler et al. (2008).