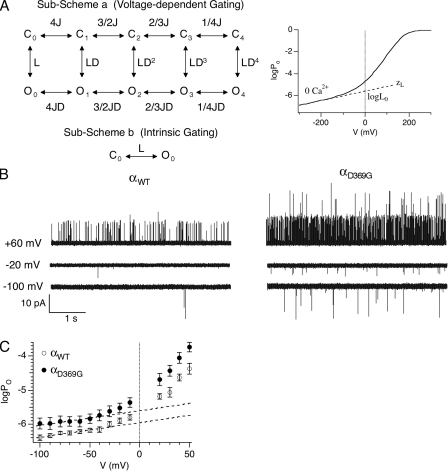
Figure 2.

D369G decreases the energetic barrier for channel to open. (A; left) According to the dual-allosteric mechanism (Horrigan et al., 1999; Horrigan and Aldrich, 2002), BK channel transitions between closed (C) and open (O) conformation is allosterically regulated by the state of four independent and identical voltage sensors. Sub-Scheme a represents BK channel’s gating scheme at 0 Ca²⁺. The channel resides in either the open or closed conformation, with 0–4 voltage sensors in the activated state. The equilibrium between C-O transitions is allosterically regulated by the states of the voltage sensors. Sub-Scheme b represents BK channel’s gating scheme at 0 Ca²⁺ and very negative voltages. With all voltage sensors in the resting state, the channel resides in one of two conformations, C₀ and O₀. The equilibrium between the C₀-O₀ transition is described by L, the intrinsic equilibrium for channel opening in the absence of Ca²⁺ and voltage sensor activation. (Right) This illustrates how two components of L (L₀ and z_L) can be estimated by logPo-V data at 0 Ca²⁺ and negative voltages. The curve represents simulated logPo versus voltage curve in nominally 0 Ca²⁺. The gating parameters used for simulation are as follows: L₀ = 2.5 × 10⁻⁶, z_L = 0.25 e₀, z_J = 0.54e₀, Vh_C = 173 mV, and Vh_O = 25 mV. Dashed line represents fit for logPo-V at limiting slope using Eq. 4. L₀ and z_L can be derived from the fit (Horrigan and Aldrich, 2002). (B) Single-channel BK currents recorded in nominally 0 [Ca²⁺] at the indicated voltages. α_WT and α_D369G data were obtained from patches containing estimated 64 and 317 channels, respectively. All traces were filtered at 5 kHz. (C) D369G increases L₀. Mean logPo plotted as a function of voltage in nominally 0 Ca²⁺ (α_WT: n = 5–13; α_D369G: n = 6–11). Error bars represent SEM. L₀ was estimated by linear fits (dashed lines) of logPo-V relations between −100 to −50 mV using Eq. 1. z_L value was set as 0.25 e₀.