Growing length and time scales in glass-forming liquids

Abstract

The glass transition, whereby liquids transform into amorphous solids at low temperatures, is a subject of intense research despite decades of investigation. Explaining the enormous increase in relaxation times of a liquid upon supercooling is essential for understanding the glass transition. Although many theories, such as the Adam–Gibbs theory, have sought to relate growing relaxation times to length scales associated with spatial correlations in liquid structure or motion of molecules, the role of length scales in glassy dynamics is not well established. Recent studies of spatially correlated rearrangements of molecules leading to structural relaxation, termed “spatially heterogeneous dynamics,” provide fresh impetus in this direction. A powerful approach to extract length scales in critical phenomena is finite-size scaling, wherein a system is studied for sizes traversing the length scales of interest. We perform finite-size scaling for a realistic glass-former, using computer simulations, to evaluate the length scale associated with spatially heterogeneous dynamics, which grows as temperature decreases. However, relaxation times that also grow with decreasing temperature do not exhibit standard finite-size scaling with this length. We show that relaxation times are instead determined, for all studied system sizes and temperatures, by configurational entropy, in accordance with the Adam–Gibbs relation, but in disagreement with theoretical expectations based on spin-glass models that configurational entropy is not relevant at temperatures substantially above the critical temperature of mode-coupling theory. Our results provide new insights into the dynamics of glass-forming liquids and pose serious challenges to existing theoretical descriptions.

Most approaches to understanding the glass transition and slow dynamics in glass formers (1–10) are based on the intuitive picture that the movement of their constituent particles (atoms, molecules, polymers) requires progressively more cooperative rearrangement of groups of particles as temperature decreases (or density increases). Structural relaxation becomes slow because the concerted motion of many particles is infrequent. Intuitively, the size of such “cooperatively rearranging regions” (CRR) is expected to increase with decreasing temperature. Thus, the above picture naturally involves the notion of a growing length scale, albeit implicitly in most descriptions. The notion of such a length scale, related to the configurational entropy S_c (see Methods), forms the basis of rationalizing (1, 6, 7) the celebrated Adam–Gibbs (AG) relation (1) between the relaxation time and S_c.

More recently, a number of theoretical approaches have explored the relevance of a growing length scale to dynamical slow down (5, 7, 9). A specific motivation for some of these approaches arises from the study of heterogeneous dynamics in glass formers (11–14). In particular, computer simulation studies (12–14) have focused attention on spatially correlated groups of particles that exhibit enhanced mobility, and whose spatial extent grows upon decreasing temperature. The spatial correlations of local relaxation permits identification of a dynamical (time dependent) length scale, ξ, through analysis of a 4-point correlation function first introduced by Dasgupta, et al. (15) (see Methods), and the associated dynamical susceptibility χ₄ (16, 17). These quantities have been studied recently via inhomogeneous mode-coupling theory (IMCT) (5) and estimated from simulation and experimental data (5, 10, 18–21).

The method of finite-size scaling, used extensively in numerical studies of critical phenomena (22), is uniquely suited for investigations of the presence of a dominant length scale. This method involves a study of the dependence of the properties of a finite system on its size. We study a binary mixture of particles interacting via the Lennard–Jones potential (23), originally proposed as a model for Ni₈₀P₂₀, and widely studied as a model glass former. We perform constant temperature molecular dynamics simulations at a constant volume [see Methods and (24) for details], for 7 temperatures, and up to a dozen different system sizes for each temperature. For each case, we calculate the dynamic susceptibility χ₄(t) as the second moment of the distribution of a correlation function Q(t), which measures the overlap of the configuration of particles at a given time with the configuration after a time t (see Methods).

Results

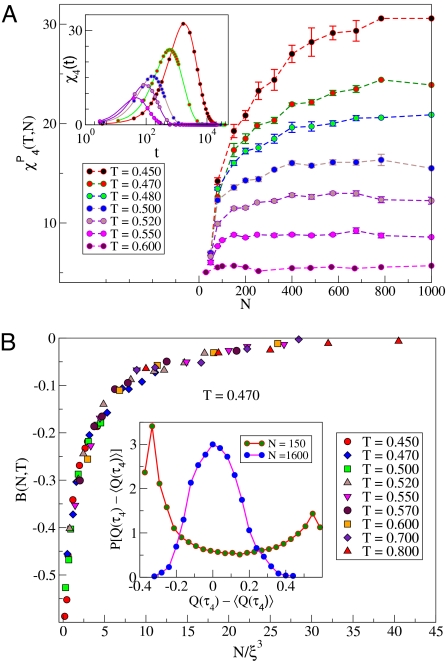
From previous work, it is now well-established that χ₄(t) has nonmonotonic time dependence, and peaks at a time τ₄ that is proportional to the structural relaxation time τ. Such behavior is shown in Fig. 1A Inset. In Fig. 1A, we show the peak values χ₄^p≡χ₄(τ₄) vs. system size (number of particles) N for a range of temperatures. At each temperature, χ₄^p is an increasing function of N, saturating at large N. The saturation occurs at a larger value of N at lower temperatures. This is the expected finite-size scaling behavior of a quantity whose growth with decreasing temperature is governed by a dominant correlation length that increases with decreasing temperature.

Fig. 1.

System size dependence of dynamic susceptibility χ₄^p, and finite-size scaling of the Binder cumulant B(N,T). (A Inset) χ₄(t), shown here for N = 1,000 and selected temperatures, exhibits nonmonotonic time dependence, and the time τ₄ at which it has the maximum value has been observed to be proportional to the structural relaxation time τ. (A) Peak height of the 4-point dynamic susceptibility, χ₄^p(T,N) ≡ χ₄(t = τ₄, T, N), has been shown as a function of system size N for different temperatures. For each temperature, χ₄^p(T,N) increases with system size, and saturates for large system sizes. χ₄^p(T,N) also increases as the temperature is lowered. (B Inset) The distribution P[Q(τ₄)−〈Q(τ₄)〉] of Q(τ₄)−〈Q(τ₄)〉 is shown for 2 system sizes for T = 0.470. Although the distribution for the large size is nearly Gaussian, the small system exhibits a strongly bimodal distribution. Such bimodality is also observed to emerge as the temperature is decreased at fixed system size. (B) Binder cumulant B(N,T) (see Methods) has been plotted as function of N/ξ³ for different temperatures in the range T ∈ [0.45, 0.80]. The correlation length ξ is an unknown, temperature dependent, scaling parameter determined by requiring data collapse for values at different T. By construction B(N,T) will approach zero for large system sizes at high temperatures. It changes to negative values as the temperature or the system size is decreased such that P[Q(τ₄)−〈Q(τ₄)〉] becomes bimodal. The correlation length ξ(T) is the only unknown to be determined to obtain data collapse for B(N,T) and the quality of the data collapse confirms the reliability of this procedure.

We have estimated the correlation length ξ from finite-size scaling of χ₄^p(T,N), which also involves estimating the value of χ₄^p as N → ∞. Because the latter estimation is a potential source of error in estimating ξ, we employ the Binder cumulant of the distribution of Q(τ₄) to estimate ξ. The Binder cumulant (25), defined (see Methods) in terms of the 4th and second moments of the distribution, vanishes for a Gaussian distribution, whereas it acquires negative values for bimodal distributions. The Binder cumulant has been used extensively in finite-size scaling analysis in the context of critical phenomena, owing to its very useful property that in systems with a dominant correlation length ξ, it is a scaling function only of L/ξ (or equivalently, of N/ξ³), where L is the linear dimension of the system. The distributions themselves are shown in Fig. 1B Inset, for 2 different system sizes for temperature T = 0.47. We see that the distribution is unimodal for the large system size of N = 1600 whereas it is strongly bimodal for the small system size of N = 150. The same trend is observed as temperature is decreased for a fixed size of the system. The data collapse of the Binder cumulant, from which we extract the correlation length ξ(T), is shown in Fig. 1(b). The collapse observed is excellent, confirming that the growth of χ₄^p with decreasing T is governed by a growing dynamical correlation length. The values of ξ obtained from this scaling analysis are consistent with less accurate estimates obtained from a similar analysis of the N dependence of χ₄^p(T,N), and from the wave-vector dependence of the 4-point dynamic structure factor S₄(q,τ₄) (see, e.g., ref. 5). Because the data collapse of the Binder cumulant is not affected by a uniform rescaling of L/ξ for all temperatures, we can determine ξ(T) only up to an unknown multiplicative constant that is common to all of the temperatures. The unknown multiplicative constant has been fixed so that the ξ value from finite-size scaling matches the value obtained from analysis of S₄(q,τ₄) at one temperature. Estimated values of χ₄^p as N → ∞ compare very well with the q → 0 limit of S₄(q,τ₄), up to a proportionality constant (described elsewhere).

The value of ξ increases from 2.1 to 6.2 as T decreases from T = 0.70 to T = 0.45. We find that both ξ and the asymptotic, N → ∞ value of χ₄^p deviate from power law behavior as the critical temperature T_MCT of mode-coupling theory (T_MCT ≃ 0.435 in our system) is approached (consistently with previous observations). However, the power-law relationship between χ₄^p and ξ predicted in IMCT is satisfied by our data. Because the range of the measured values of ξ is small, it is difficult to obtain accurate estimates of the exponents of these power laws.

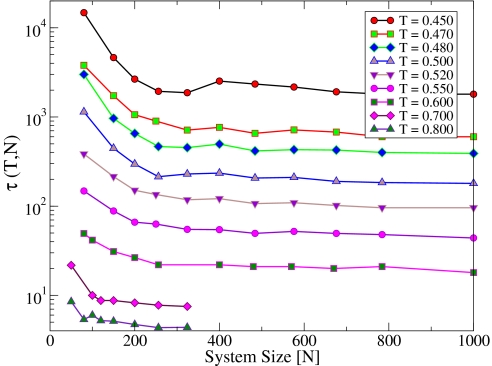
Next we consider the dependence of the relaxation time τ on T and N. For each case, we calculate the relaxation time from the decay of 〈Q(t)〉. The results for τ are displayed in Fig. 2, which shows that τ increases as the temperature decreases, as expected. However, the observed increase in τ with decreasing N for small values of N at fixed T is not consistent with standard dynamical scaling for a system with a dominant correlation length (e.g., near a critical point): dynamical finite-size scaling would predict a decrease in τ as the linear dimension L of the system is decreased below the correlation length ξ*. Similar finite-size effects on relaxation times have been observed in previous simulations of realistic glass formers (e.g., ref. 26) but have not been analyzed in detail. Due to computational limitations, our simulations cover a (relatively) high-temperature regime, the lowest temperature considered being slightly above the mode-coupling temperature T_MCT for this system. However, it is clear from Fig. 2 that the N dependence of τ becomes stronger and persists to larger values of N as the temperature is decreased. Therefore, the deviations of the N dependence of τ from standard dynamical finite-size scaling are expected to be more pronounced at temperatures near the actual glass transition. The N dependence of τ shown in Fig. 2 is opposite to that found in finite-size scaling studies of some spin-glass models (27) but similar to that found in other studies (ref. 28 and Biroli G, personal communication).

Fig. 2.

Relaxation times as a function of temperature and system size. Relaxation time τ(T,N) for the largest system size increases approximately by 3 decades from the highest to the lowest temperature shown. For each temperature, τ(T,N) increases as N is decreased for small values of N, displaying a trend that is opposite to that observed near second order critical points. For the smallest temperature, τ(T,N) increases by approximately a decade from the largest to the smallest system size.

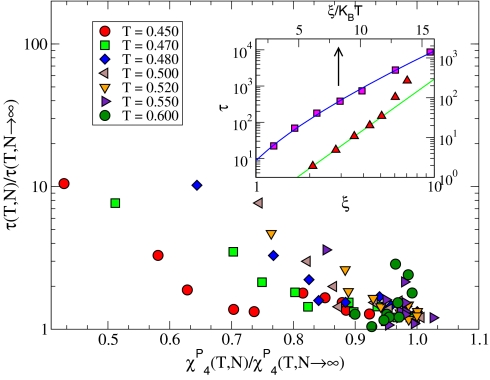
Fig. 3Inset shows the large-N value of τ plotted as a function of (bottom curve) the correlation length ξ on a double-log scale, and (top curve) $\frac{\xi }{k_{\text{B}}T}$ on a semilog scale. The power-law relation between these 2 quantities predicted in IMCT (5) is found above T = 0.5; deviation from a power law is found at lower temperatures. The semilog plot indicates that an exponential form τ ∼ exp(k(ξ/k_BT)^ζ), with ζ = 0.7, describes the data well in the entire range. Although such a dependence is expected according to the random first order theory (RFOT) (7), the exponent value we observe cannot be easily rationalized within that framework. We comment further on the significance of the exponent value later. Fig. 3 shows relaxation times τ(T,N) for different N values scaled to the asymptotic N → ∞ value τ(T), plotted against values of χ₄^p(T,N) scaled to the asymptotic N → ∞ value χ₄^p(T). If the system size dependence of τ and χ₄^p are governed by the same length scale, one must expect a universal dependence of the scaled relaxation times on the scaled χ₄^p values. From the data shown in Fig. 3, it is clear that there is no universal relation between the scaled τ and χ₄^p that describes their variation both with T and with N. These results indicate that the observed N dependence of τ is not consistent with standard finite-size scaling with the length scale of dynamic heterogeneity.

Fig. 3.

Relationship between the relaxation time τ(T,N), correlation length ξ(T) and the dynamic susceptibility χ₄^p(T,N). (Inset) τ(T,N → ∞) is shown against ξ(T), in a log-log plot (bottom curve). This plot shows that a power-law dependence holds over a temperature range above T = 0.5, but breaks down at lower temperatures. τ(T,N → ∞) is shown against ξ(T)/k_B T, in a semilog plot (top curve). This plot shows that an exponential dependence τ∼ exp(k(ξ/k_BT)^ζ), with ζ = 0.7, describes the data well in the entire temperature range. However, the observed exponent value ζ = 0.7 is difficult to explain with existing theories. The surrounding semilog plot shows relaxation times τ(T,N)/τ(T,N → ∞) against χ₄^p(T,N)/χ₄^p(T,N → ∞). Although at fixed N both τ and χ₄^p increase upon decreasing T, at fixed T, they show opposite trends, with τ increasing for decreasing N and χ₄^p increasing for increasing N. If τ and χ₄^p are determined by the same length scale ξ and further, if their finite-size behavior is governed by N/ξ³, the plotted data are expected to lie on a universal curve, which is seen not to be the case.

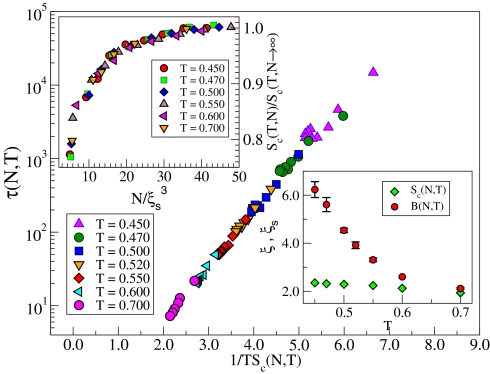
Motivated by the AG relation (1), τ∝ exp $\left(\frac{A}{T{S}_c}\right)$ where A is a constant, we next consider the dependence of τ on the configurational entropy S_c whose evaluation is described elsewhere (24). As shown in Fig. 4 where log(τ) is plotted vs. $\frac{1}{T{S}_c}$ for all temperatures and system sizes studied, we find a remarkable agreement with the AG relation, not only vs. T but also for all system sizes. To our knowledge, such a demonstration of the validity of the AG relation for finite or confined systems has not been made earlier. Thus, the N dependence of τ, which cannot be understood from dynamical finite-size scaling, can be explained in terms of the N dependence of S_c, suggesting that the growth of τ with decreasing temperature is more intimately related to the change of S_c, than to the increase of the correlation length ξ and susceptibility χ₄ predicted in IMCT. Because S_c at a given temperature varies with system size N, it is tempting to inquire whether the N dependence of S_c is associated with a length scale. We extract such a length scale from data collapse of S_c(T,N), scaled to its value as N → ∞, shown in the Fig. 4 Upper Inset. We obtain reasonable data collapse, but the extracted length scales turn out to have substantially weaker T dependence compared with ξ, as shown in the Fig. 4 Lower Inset.

Fig. 4.

The dependence of relaxation times τ on the configurational entropy S_c. The relaxation times are shown against configurational entropy in an “Adam–Gibbs” plot [log(τ) vs. 1/(TS_c)], for all of the temperatures and system sizes studied. The impressive data collapse of all of the data onto a master curve indicates that the configurational entropy is crucial for determining the relaxation times. The overall behavior is well described by the AG relation, which requires log(τ) ∝ 1/(TS_c). Although other powers of 1/(TS_c) may also describe the data well, the improvement in fit quality is marginal, and hence we treat the data presented as validating the AG relation. (Upper Inset) The configurational entropy S_c(T,N) scaled to its N → ∞ value, has been plotted as function of N/ξ_s³ for different temperatures in the range T ∈ [0.45, 0.80], to extract a temperature dependent length scale ξ_s that leads to data collapse. (Lower Inset) The length scale obtained from the data collapse of the configurational entropy (green diamonds) compared with the length scale obtained from finite-size scaling of the Binder cumulant (red triangles). It is apparent that the length scale from configurational entropy shows very weak temperature dependence, in contrast with the dynamical heterogeneity length scale.

Discussion

A central role for the configurational entropy, along with an analysis of a length scale relevant to structural relaxation, are the content of the random first order theory, developed by Wolynes and coworkers (7). According to RFOT, the length scale of dynamical heterogeneity is the “mosaic length” ξ_m that represents the critical size for entropy driven nucleation of a new structure in a liquid. Mean-field arguments based on known properties of infinite-range models suggest that the RFOT mechanism is operative for temperatures lower than T_MCT. In this regime, the dynamics of the system is activated, with the relaxation time expected to vary as τ = τ₀ exp $\left[B{\left(\frac{\Delta F}{k_{B}T}\right)}^{\psi }\right]$ where ΔF is the free energy barrier to structural rearrangements, and ψ is an unknown exponent. The free energy barrier in turn depends on the mosaic length as $\frac{\Delta F}{k_{B}T}$ ∼ ξ_m^θ, where θ describes the dependence of the surface energy on the size of a region undergoing structural change. Further, the configurational entropy is related to the mosaic length as ξ_m∼1/(TS_c) $\frac{1}{d-\theta }$, and thus, τ∼exp[A/(TS_c) $\frac{\theta \psi }{d-\theta }$ If we interpret the length scale ξ as the mosaic length ξ_m (29),^† then the observed validity of the AG relation (which requires $\frac{\theta \psi }{d-\theta }$ = 1), and the dependence of the relaxation time on the length scale ξ, τ ∼ exp(k(ξ/k_BT)^ζ), with ζ = θψ = 0.7, can be rationalized within RFOT if the exponent θ is assumed to be close to 2.3, and the exponent ψ is close to 0.3. However, this interpretation has the drawback that the exponent θ does not satisfy the physical bound, θ ≤ 2, in 3 dimensions, and there is no evident explanation for the value of ψ. We note that similar conclusions were reached in a recent analysis (21) of experimental data near the laboratory glass transition, on a large class of glass-forming materials. Thus, we find puzzling values for the exponents relevant to the applicability of RFOT, which are in need of explanation, and data in (21) indicate that such a result may apply for a wide range of temperatures, all of the way to the experimental glass transition.

RFOT focuses on behavior near the glass transition, and in the limiting case of the spin glass models where theoretical perditions are available, configurational entropy plays no role in the behavior of the system above the mode-coupling temperature. However, there have indeed been attempts to extend the RFOT analysis to temperatures above the mode-coupling temperature (30–32) and to estimate a mosaic length scale at such temperatures, and we thus compare our results with predictions arising from these analyses. Stevenson, et al. (30) have considered the change in morphology of rearranging regions above the mode-coupling temperature, and correspondingly the dependence of relaxation times on configurational entropy. The predicted dependence of relaxation times on configurational entropy differs from the Adam–Gibbs form, whereas our results strikingly confirm the Adam–Gibbs form. Franz and Montanari (31) have estimated a mosaic length scale in addition to a heterogeneity length scale, and have discussed the cross-over in the dominant length scale near the mode-coupling temperature. However, this analysis does not contain explicit predictions regarding the relevance of the configurational entropy at temperatures higher than the mode-coupling temperature.

Our observation that the configurational entropy predicts the relaxation times in accordance with the AG relation for all of the temperatures and system sizes we study poses serious challenges to current theoretical descriptions based on the analogy with the behavior of mean-field models. Although the relevance of the configurational entropy at high temperatures has been observed in earlier simulation studies and analyses based on the inherent structure approach (24, 33, 34), we emphasize that a theoretical analysis that satisfactorily explains such dependence is not at hand at present, and our results concerning the robustness of the Adam–Gibbs relation in finite systems highlights further the challenge to existing theoretical descriptions. Indeed, earlier work (28, 35) has highlighted the puzzle that aspects of the energy landscape and mode-coupling theory descriptions appear to apply over a significant temperature range side by side, rather than in neatly separated temperature regimes as expected from mean field theoretical descriptions. Our results emphasize the importance of understanding such overlap of temperature regimes and relaxation mechanisms, which has recently been addressed in (32). Equally importantly, our results indicate that the length scale that describes the growth of dynamical heterogeneity in IMCT may not play the central role attributed to it in recent analyses, and highlights the necessity to understand the role of other relevant length scales, along the lines of the analysis in ref. 31.

Methods

Simulation Details.

The system we study is a 80:20 (A:B) binary mixture of particles interacting via the Lennard–Jones potential:

where α,β ∈ {A,B} and ε_AB/ε_AA = 1.5, ε_BB/ε_AA = 0.5, σ_AB/σ_AA = 0.80, σ_BB/σ_AA = 0.88, masses m_A = m_B. The interaction potential is cutoff at 2.50σ_αβ. Length, energy and time are reported in units of σ_AA, ε_AA and $\sqrt{{\text{σ}}_{\text{AA}}^{\text{2}}/{\text{ε}}_{\text{AA}}}$, and other reduced units are derived from these. All simulations are done for number density ρ = 1.20. We have used a cubic simulation box with periodic boundary conditions. Simulations are done in the canonical ensemble (NVT), using a modified leap-frog integration scheme. We simulate for 7 temperatures in the range T ∈ {0.450, 1.00}. The mode-coupling temperature for this system has been estimated (23) to be T_MCT ≃ 0.435. We equilibrate the system for ≈10⁷ − 10⁸ MD steps depending on system size and production runs are at least 5 times longer than the equilibration runs. We use integration time steps dt from 0.001 to 0.006 for the temperature range 0.800 to 0.450. The studied system sizes vary from N = 50 to N = 1,600.

Dynamics.

Dynamics is studied via a 2 point correlation function, the overlap Q(t),

where ρ(r→,t₀) etc are space-time dependent particle densities, w(r) = 1, if r ≤ a and zero otherwise, and averaging over the initial time t₀ is implied. The use of the window function [a = 0.30] treats particle positions separated due to small amplitude vibrational motion as the same. The second part of the definition is an approximation that uses only the self-term, which we have verified to be reliable (see ref. 17 for details). The structural relaxation time τ is measured by a stretched exponential fit of the long-time decay of Q(t).

The fluctuations in Q(t) yields the dynamical susceptibility:

Ref. 17 shows that χ₄(t) reaches a maximum for times τ₄ which are proportional to the structural relaxation time τ. We report the values of χ₄^p ≡ χ₄(t = τ₄).

The Binder cumulant, which we use for finite-size scaling, is defined as

B(N,T) = 0, if the distribution P(Q(τ₄)) is Gaussian, and is a scaling function of ξ/L only (where L is the linear size of the system, and ξ is the correlation length), without any prefactor.

Configurational Entropy.

S_c, the configurational entropy per particle, is calculated as the measure of the number of distinct local energy minima, by subtracting from the total entropy of the system the “vibrational” component:

Details of the calculation procedure are as given in ref. 24.