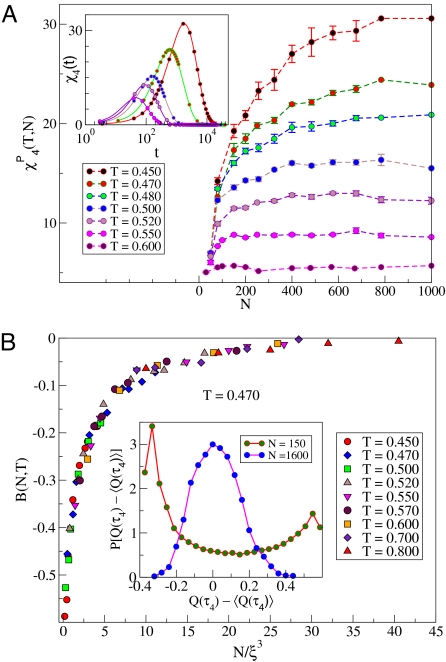
Fig. 1.

System size dependence of dynamic susceptibility χ₄^p, and finite-size scaling of the Binder cumulant B(N,T). (A Inset) χ₄(t), shown here for N = 1,000 and selected temperatures, exhibits nonmonotonic time dependence, and the time τ₄ at which it has the maximum value has been observed to be proportional to the structural relaxation time τ. (A) Peak height of the 4-point dynamic susceptibility, χ₄^p(T,N) ≡ χ₄(t = τ₄, T, N), has been shown as a function of system size N for different temperatures. For each temperature, χ₄^p(T,N) increases with system size, and saturates for large system sizes. χ₄^p(T,N) also increases as the temperature is lowered. (B Inset) The distribution P[Q(τ₄)−〈Q(τ₄)〉] of Q(τ₄)−〈Q(τ₄)〉 is shown for 2 system sizes for T = 0.470. Although the distribution for the large size is nearly Gaussian, the small system exhibits a strongly bimodal distribution. Such bimodality is also observed to emerge as the temperature is decreased at fixed system size. (B) Binder cumulant B(N,T) (see Methods) has been plotted as function of N/ξ³ for different temperatures in the range T ∈ [0.45, 0.80]. The correlation length ξ is an unknown, temperature dependent, scaling parameter determined by requiring data collapse for values at different T. By construction B(N,T) will approach zero for large system sizes at high temperatures. It changes to negative values as the temperature or the system size is decreased such that P[Q(τ₄)−〈Q(τ₄)〉] becomes bimodal. The correlation length ξ(T) is the only unknown to be determined to obtain data collapse for B(N,T) and the quality of the data collapse confirms the reliability of this procedure.