Abstract
The study addresses three main questions: (1) Does the magnitude of the grasping force affect the prehension synergies, i.e. conjoint changes of finger forces and moments? (2) Do individual finger forces scale with the total grasping forces (‘scale-invariance hypothesis’)? (3) How specification of the grasping force magnitude affects the inverse optimization of digit forces. Subjects (n=7) grasped with minimal force an instrumented handle and maintained it at rest in the air. Then, the subjects doubled the initial grasping force. The forces and moments exerted by individual digits were recorded with 6-component sensors. External torques that the subjects should resist (9 in total) varied among the trials from zero to 0.46 Nm both in clockwise and counterclockwise directions. After the force doubling, the moments of the normal forces (Mn) increased in the pronation effort tasks (PR-tasks) and decreased in the supination effort tasks (SU-tasks). The changes in the moments of the tangential forces (Mt) were opposite to the Mn changes; the moments increased in the SU-tasks and decreased in the PR-tasks. The opposite effects of force doubling on the Mts in the SU-tasks and PR-tasks were a consequence of the unidirectional changes of the thumb tangential forces: in all the tasks the contribution of the thumb tangential force to the total tangential force increased after the grasping force doubling (and the total contribution of the four fingers decreased). The decrease of the virtual finger (VF) tangential force was mainly due to the decrease of the index finger force (VF is an imagined finger that exerts the same force and moment as all the fingers together). In the non-zero torque tasks the individual finger forces did not scale proportionally with the grasping force, the sharing percentage of the individual finger forces in the VF normal force changed with the grasping force increase. The root mean square (RMS) differences between the actual finger sharing percentages in the VF force and the sharing percentages predicted from optimization procedures in which different cost functions were used were in all cases smaller after the doubling than before the doubling. Hence the answers to the three questions formulated above are: (1) the alteration of the grasping force magnitude induces complex coordinated changes of all digit forces and moments; (2) the scale invariance hypothesis is confirmed only for the zero-torque tasks and rejected for the non-zero tasks, and (3) the specification of the grasping force magnitude at the level of twice the initial grasping force —which essentially restricts the control task to the object tilt prevention—improves the accuracy of the employed optimization procedures.
Keywords: grasping, prehension synergy, redundancy, digit forces, doubling
INTRODUCTION
In this study, subjects grasped with a minimal force an instrumented handle and kept it at rest in the air; then they doubled the grasping force while still maintaining the handle at rest. The study is motivated by three considerations.
When people manipulate hand-held objects, for instance, to keep an object at rest in the air, the performers distribute the digital normal and tangential forces to satisfy the task requirements. Because the number of degrees of freedom of the object, totally six, is smaller than the degrees of freedom of a five-digit hand, the task is mechanically redundant, i.e. the same task can be performed by various combinations of the digit forces and moments (Latash et. al. 2003; Latash 2008). In spite of the task redundancy, similar prehension tasks are performed by people more or less similarly (Zatsiorsky et al. 2003). Still some inter-individual differences exist. In particular the performers grasp the object with different forces; they may share individual digit forces in their own way, etc. (Zatsiorsky et al. 2003). This may happen due to many reasons (e.g. different understanding of the instruction, different sensitivity of skin receptors, different skin friction, etc). We leave however these questions for the future and are interested in this study in the following question: does the magnitude of the grasping force affect the prehension synergies, i.e. conjoint changes of finger forces and moments?
It has been reported in the literature that human performers alter the magnitude of the total force produced by several contributing elements by scaling the forces generated by the individual elements. If the direction of the total force is constant but the magnitude is scaled, the contributing forces as well as muscle activations also scale (the so-called ‘scale invariance’ – Pan et al. 2005). The examples are: (a) the total grasping force in multi-finger grasping: at any combination of friction values at the individual fingertip-object contacts the performers select a certain ‘template’ of digit forces and then scale it linearly with the weight of the hand-held object (Niu et al. 2007), (b) static arm force generation of different magnitude at various force directions and arm postures (Pan et al. 2005), (c) four-finger ramp force production (Li et al. 1998), (d) isometric contractions of human elbow muscles (Buchanan et al. 1986), and (e) the voluntary force production by the index finger (Valero-Cuevas 2000). In (d) and (e) the contributing muscles and their relative activity did not change with the force magnitude. The force was controlled by scaling the magnitude of a constant coordination pattern. However it was hypothesized (Niu et al. 2007) that scaling of a certain template is not a universal mechanism of force control. In particular this mechanism is only valid for prehension tasks with zero moment production. The second goal of the present study was to test this hypothesis. For experimental analysis of this problem, we selected a task of doubling the total grasping force while preserving the orientation of the object in space. This task required the subjects to keep the total moment of force constant while the moment produced by the normal (grasping) force could change if properly balanced by changes in the moment of the tangential forces. The scaling of the finger normal forces in the non-zero torque prehension tasks would change the moment of the normal forces exerted on the object and hence may lead to the object rotation. This option however does not discard completely the finger force scaling as a feasible mechanism of the total force control. The moment of the normal forces can be negated by generating an opposite moment of tangential forces (Zatsiorsky et al. 2002 a, b). Hence, the scaling of the normal forces is still a viable strategy of grip force control (provided that the tilt prevention is achieved by the concomitant adjustments of the tangential forces). Due to the mechanical redundancy, the pattern of force adjustments after the total force doubling — (a) scaling the normal finger forces with concomitant adjustments of the tangential forces to maintain the total moment constant, or (b) the coordinated changes of the normal forces to maintain the moment of the normal forces constant—cannot be immediately predicted from the mechanical analysis and should be established experimentally. Hence, the second goal of the present study was to test the ‘scale invariance’ hypothesis, whether the pattern (a) above is valid. Note that in the prehension tasks, the scale invariance hypothesis can be valid only for the normal finger forces. If the finger force vectors do not change their direction, the tangential forces will increase with the rise of the normal forces and the object equilibrium will be broken; the object will accelerate in the vertical direction.
An additional goal of the study was to explore effects of the grasping force specification on the inverse optimization of digit forces in grasping. This aspect of research requires a special explanation. Because people perform similar tasks, e.g. walking or grasping, more or less similarly and in a certain sense efficiently, it is commonly accepted that the central controller selects a movement pattern or force distribution pattern optimally by minimizing a certain cost function(s) (for reviews see Crowninshield, Brand 1981;Tsirakos et al. 1997; Engelbrecht 2001; Prilutsky, Zatsiorsky, 2004; Erdemir et al. 2007). For the human prehension several probable cost functions have been explored (Hershkovitz et al., 1995, 1997; Zatsiorsky et al. 2002b) with some of the functions borrowed from robotic research on grasping (Hershkovitz et al., 1995; Salunkhe et al. 1998; Buss et al. 1996). Since the pioneering study of Nubar and Contini (1961) the main idea behind the employed cost functions was that a certain measure of muscular effort is minimized, e.g. the sum of squared muscle moments of force (Nubar, Contini 1961), the weighted norm of the joint torque vector (Baud-Bovy et al. 2005); the sum of the cubed muscle stresses (Crowninshield 1978; Stokes, Gardner-Morse 2001), ‘global muscular effort’, i.e. the sum of squared values of the muscle forces normalized with respect to their maximal magnitudes (Chalfoun et. al. 2004), overall maximum tendon stress (Fowler, Nicol 2000), sum of muscle stresses squared (Brook et al. 1995), an entropy-like function that assumes a minimal value when the total force generated by several fingers is distributed equally among the fingers (Hershkovitz et al. 1995, 1997), the strain energy of the soft finger pad tissue (Pataky 2005), and the central neural commands that take into account the finger interdependence (Zatsiorsky et al. 2002a,b). For instance, a reasonable candidate for the cost function in prehension may be a particular function of digit forces, such as their Eucledian norm or the sum of the cubed values, either absolute (in newtons) or relative (in %% of the maximal force), etc. All of these functions are based on an assumption that prehension is optimal or close to optimal if the exerted forces are either minimal or are at least small.
Differently from the earlier studies on the finger force optimization in multi-finger prehension (Zatsiorsky et al. 2002; Pataky et al. 2004a,b; Aoki et al. 2007), in the present experiment the total normal force exerted by the digits was prescribed (twice the magnitude observed during a comfortable “minimum effort” grasp). Hence, after force doubling the total grasping force was not an optimized variable anymore; it was an optimization constraint. We were interested in knowing how this modification affects optimization results, specifically we explored the ability of the various cost functions to predict finger forces in multi-finger prehension. While this question may give the impression of being ‘pure technical’, i.e. related more to mathematical method of optimization itself than to the issues of motor control, there is also a significant motor control aspect here.
According to the principle of superposition the control of multi-finger prehension can be viewed as a superposition of two independent synergies controlling the grasping force (‘slip prevention synergy)’ and the orientation of the object (‘’tilt prevention synergy”), respectively (Zatsiorsky et. al. 2004). An optimization procedure when the grasping force is not specified should satisfy the two above requirements, i.e. to prevent both the slip and the tilt. After the grasping force doubling the slip prevention is not a problem anymore, and the force optimization is restricted only by the necessity to prevent object tilt.
METHODS
1. Subjects
Seven male subjects participated in the experiment (age 27.7±2.2 years, weight 69.8±8.5 kg, height 1.77±0.08 m, hand length from the middle fingertip to the distal crease of the wrist with hand extended 18.8 ± 1.3 cm, hand width at the MCP level with hand extended 9.1±0.9 cm). The subjects were all right-hand dominant and had no history of neuropathy or trauma to their upper limbs. All subjects gave informed consent according to the policies of the Office for Research Protections of The Pennsylvania State University.
2. Apparatus
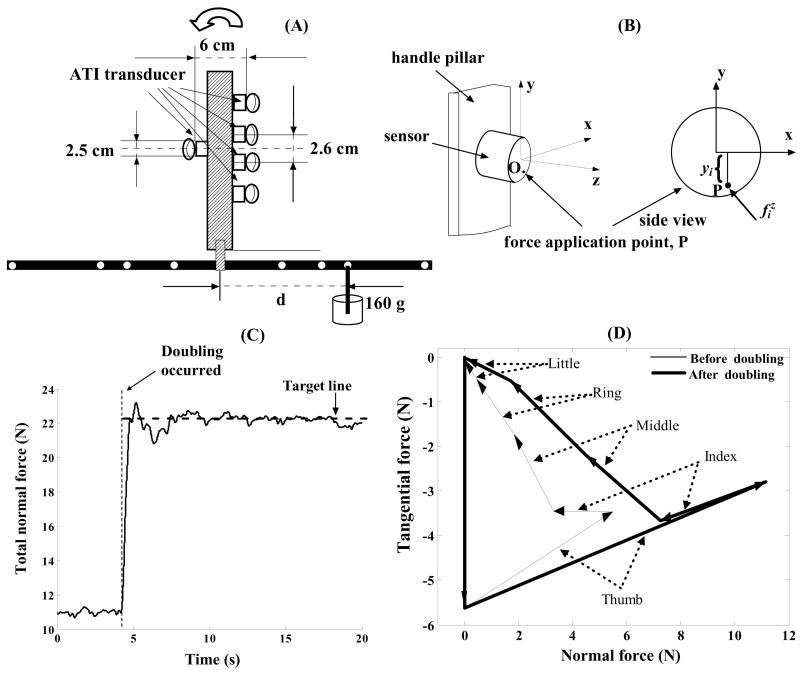
Five six-component force/moment transducers (Nano-17, ATI Industrial Automation, Garner, NC, USA) were mounted on an aluminum handle at the bottom of which a horizontal aluminum bar was attached (70 cm long, Figure 1 A). An air bubble level was positioned at the top of the handle to help the subjects keep the handle vertical. The level (diameter: 32 mm) included a central circle (diameter: 15 mm) and an air bubble (diameter: 5mm) in the enclosed liquid. If the bubble was within the central circle, the trial was accepted by the researcher; otherwise the trial was repeated. We found that when the moment of force exerted by the subject was within ±40 Nmm (0.04 Nm) of the target level, the bubble was at the edge of the central circle. Four transducers were used to measure forces and moments of force applied by the fingers, and the fifth transducer measured the force and moment of force produced by the thumb. The centers of all five sensors were in one plane (the grasp plane).
Figure 1.
The experimental apparatus and recorded forces. (A) Schematic drawing of the apparatus with five sensors mounted on a handle with a T-shaped attachment. (B) Local coordinates on each transducer. (C) Total normal force generated to match the target line after 4 seconds of natural grasping. (D) Digit force vectors recorded before and after doubling. The force polygons are obtained by adding tail-to-head the individual digit forces. Starting from the upper left corner the following forces are shown: gravity, the thumb, index, middle, ring and little finger force. Ideally, in static conditions the polygon should close. Panels (C) and (D) are representative examples, R1 task.
The distance between two finger sensors was 2.6 cm, and the thumb sensor was positioned across the midpoint between the centers of the middle and ring finger sensors. The combined mass of the handle, sensors, and the bar was 415g. During the experiments, a 160g load was attached at different points along the bar. The load suspension at different locations generated nine external torques: 0.14 Nm, 0.23 Nm, 0.28 Nm and 0.46 Nm clockwise and counterclockwise, as well as a zero torque. In the ensuing text and figures, the external torques 0.46 Nm, 0.28 Nm, 0.23 Nm, 0.14 Nm, 0 Nm, −0.14 Nm, −0.23 Nm, −0.28 Nm and −0.46 Nm are designated as L4, L3, L2, L1, Mi, R1, R2, R3, and R4, respectively. The designations represent the position of the load along the bar on the left (L) or on the right (R) from the handle. Since in the Li tasks (i =1, 2, 3, 4) the handle tilt was prevented by supination efforts, these tasks were called “Supination Effort Tasks” (SU-tasks). The Ri tasks were called “Pronation Effort Tasks” (PR-tasks). In the finger arrangement shown in Figure 1 A two fingers (the index and middle) are located above the thumb and the other two fingers (the ring and little) are located below the thumb. These finger pairs exert moments of force in the opposite directions with respect to the thumb as a pivot. If in a given task the moments generated by individual finger(s) force resist external torque, i.e. they prevent the handle tilt, the fingers will be called moment agonists, if the moments assist external torque, i.e. the effect of their action is opposite to the task requirement, the corresponding fingers will be called moment antagonists (Zatsiorsky et al. 2002a).
3. Experimental Procedure
Before the experiment, subjects were given an orientation session to familiarize themselves with the experimental tasks and apparatus. Then, subjects washed their hands to normalize skin condition.
The subject sat in a chair with the right upper arm positioned at approximately 45° abduction in the frontal plane and 30° flexion in the sagittal plane. The elbow joint was flexed approximately 90°. The forearm was pronated 90° such that the hand was in a natural grasping position. A computer monitor located in front of the subject showed the total normal force exerted by the subject on the handle. The subjects were coached to keep the handle vertically by looking quickly at the bubble level located at the top of the handle while mainly watching the monitor. Each trial in the experiment consisted of two stages: grasping with natural force (4 seconds) and doubling grasping force (16 seconds). The target for the force doubling was presented as the horizontal line on the force-time graph (Figure 1 C)
Subjects were instructed to take the handle from the rack and keep the handle vertically and statically in the air by monitoring the air bubble level. When the handle was stabilized and natural grasping force was applied by the subject, the trial would start. In the first 4 seconds, the total normal force was collected and averaged. From the fifth second, a target line at the double force value of the average force of the first four seconds was demonstrated on the screen. The instruction from the investigator to the subject was: “Keep the handle vertical but match the target line by increasing the gripping force”. After the data collection in a trial stopped, the subjects placed the handle back on the rack and took a 60-s break. The investigator would change the location of the load along the bar, and informed the subject that he could start the next trial. Sensor signals were set to zero prior to each trial.
The order of external torques was randomized. Three trials were conducted for each torque combination. Each trial took 20 seconds. At least one-minute breaks were provided between two consecutive tasks. The total duration of each experiment was approximately one hour.
4. Data analysis
Software written in LabVIEW (National Instruments, NC, USA) was used to convert digital signals into the force and moment of force values. Data processing was performed using Matlab software package (Mathworks, In., Natick, MA, USA). The raw force/moment data were filtered with a third-order, zero-lag Butterworth low-pass filter at 10 Hz.
In further text, symbols m and f designate a digit moment of force and force, respectively. Subscript i refers to the ith digit, such as the thumb (th), index (in), middle (mi), ring (r) and little finger (l). Subscript VF is for the virtual finger. A virtual finger (VF) is an imagined finger that exerts the same force and moment as all the fingers together (Arbib et al. 1985; Iberall, 1987; Santello and Soechting 1997; Baud-Bovy and Soechting 2001). Superscripts x, y, or z represent the axes with respect to which the force or moment were determined. In the transducer-fixed reference system, forces normal to the transducer surface corresponded to the z direction fz. In this experiment, fz was oriented horizontally. At equilibrium states, the tangential force acted in the vertical direction fy.
The digit contacts with the sensors were modeled as the soft-finger-contacts (Murray et al. 1994); in particular rolling and deforming the fingertips were allowed. The vertical coordinates (y) of the digit force application with respect to the sensor center were computed as is the moment of the ith digit with respect to x-axis (horizontal axis), is the force of the ith digit in the z direction (Figure 1 B).
The vertical coordinate of the point of VF normal force application with respect to the point of application of the thumb force was determined based on the theorem of moments as , where Yi is the vertical coordinate of the force application point of finger i. Yi equals the algebraic sum of (1) the vertical coordinate of the sensor center in the handle fixed reference system (e.g. 15 mm for the index finger and −15 for the middle finger), (2) the displacement of the point of application of the thumb force with respect to the center of the thumb sensor, and (3) yi, the displacement of the application point of the finger i’s normal force with respect to the sensor center. In the following Yvf will be referred to as the moment arm of the VF normal force. is the sum of the normal forces produced by the four fingers. Note that a capital letter, such as Y, is used to designate a coordinate in the handle fixed reference system, while the lowercase letter like y designates the coordinate with respect to the center of a sensor.
At the VF level, the moment of normal forces Mn and the moment of the tangential forces Mt were computed. The moment of normal forces was computed as , and the moment of tangential forces was computed as , where w is the width of the handle (60 mm). Mn is the moment produced by the force couple consisting of the thumb and VF normal forces. Because the moment of a couple is a free moment, Mn can be added to Mt to obtain the total moment exerted by the subject. Upward tangential forces, the thumb normal forces, and the counterclockwise moments were defined as positive.
5. Synergy definition
The following operational definitions of the normal force synergy (grasping synergy), tangential force synergy and the moment-of-force synergy are adopted in this study:
-
Normal force synergy is defined as co-variation of the normal forces of the thumb and VF that satisfies the equation:
(1) -
Tangential force synergy is defined as co-variation of the tangential forces of the thumb and VF that satisfies the equation:
(2) where Load is the total weight of the object; FLOAD = 5.83 N in this study.
-
Moment of force synergy is defined as co-variation of the moments produced by the normal and tangential forces that satisfies the equation:
(3) where Mtot, Mn, Mt are the total moment of force, moment of normal forces and moment of tangential forces exerted by the subjects, respectively.
Note that the term ‘synergy’ in the present context refers to the co-variations of forces that satisfy the above equations not to the equations themselves. The finger forces are not constant. They vary (in the trial, among the trials, etc.). Some of these variations break the object equilibrium while others are coordinated in such a way that the equilibrium is preserved. The term ‘synergy’ refers to the second type of covariation only (for a more detailed analysis of the concept of synergy see Latash et al. 2007; Latash 2008).
6. Statistical analysis
All the data were averaged over the three trials at each condition. ANOVA and MANOVA with and without repeated measures and paired Student’s t-tests were used. Significant effects were further explored using Tukey’s pair-wise comparisons. The data were checked for sphericity in the repeated measures ANOVA test. When the requirements for the sphericity of the repeated measure ANOVA test were violated (which happened only in two of 17 RM–ANOVA tests), the degrees of freedom were corrected with the Greenhouse-Geisser method. The significance level was set as 0.05. Statistical analyses were performed in the statistics toolbox of Minitab 13.0 (Minitab, Inc., State College, PA, USA) and SPSS (SPSS Inc., Chicago, IL, USA).
7. Accuracy of the data
To check the data for accuracy, the following comparisons have been regularly performed for all trials: (a) the normal forces of the thumb and VF at equilibrium should add up to zero; (b) the total tangential force at equilibrium should equal the weight of the object; (c) the total moment of force should counterbalance the external torque; (d) the total normal force (the sum of the magnitudes of all digit normal forces) is doubled in the second experiment stage. To visualize whether the requirements were satisfied the force polygons were drawn (Figure 1 D). The equilibrium requirements were satisfied with high accuracy: the maximum standard deviation of the difference between the VF and thumb normal forces among all subjects across the tasks were below 0.24 N before and after the doubling (which simply indicates that the handle was not oscillating in the horizontal direction). The maximum standard deviations of the vertical component of the total force applied to the handle among all subjects were below 0.04 N before and after the doubling (hence the handle did not oscillate significantly in the vertical direction either). Small deviations between the computed values of the total moment of force and the external torque have been observed (Figure 2). With the exception of the L4 task, the deviation did not exceed 0.015 Nm which is a very small number. The largest deviation (0.034 Nm, or 7.3% of the target moment) occurred in L4 which is the most difficult supination task. Since the little finger which is the main torque agonist in this task is the weakest among all fingers and not as dexterous as index finger, it was difficult for the subjects to perform the task accurately. The observed discrepancies did not distort the general tendencies of the findings and were neglected in the future analysis.
Figure 2.
The actual and target moments of force exerted on the handle.
8. Optimization
We used three objective functions that were employed previously to study multi-finger prehension in human performers (Hershkovitz et al. 1995, 1997; Zatsiorsky et al. 2002b; Pataky et al. 2004a,b). The necessary equality and unequality constraints on the digit forces, similar to the used in the above mentioned papers, were incorporated into the optimization procedures. The optimization computations were performed twice, for the data before and after the force doubling. The optimization before the doubling treated the total normal force (defined above) as an optimized variable while in the optimization procedure employed for the post-doubling data the total normal force (the grasping force) was treated as an equality constraint. In the both cases, the constraints formed convex regions. Because the optimization functions are also convex, the optimal solutions were unique.
1. Energy-like function over Ft and Fn. This measure is proportional to the potential energy of deformation for a linear, e.e. Hookian, system (Hershkovitz et al. 1997).
| (3) |
where and are individual finger’s normal and tangential forces, respectively. Although F1 explicitly addresses only external contact forces, this function has been proposed to be related to minimization of muscular effort (Hershkovitz et al. 1995, 1997).
2. Cubic norm function over Fn:
| (4) |
This function was selected because of two reasons. Firstly, it has been proposed that the tangential digit forces Ft are passive consequences of external loading and the selected Fn, i.e. that the CNS is concerned only with the Fn coordination (Pataky et al. 2004b). Thus the inclusion of only Fn in a cost function is appropriate. Secondly, when a quadratic function over Fn similar to F1 was used in the optimization procedure the differences between the application of F1 and this quadratic function practically did exist. Based on that we decided to employ the cubic norm function F2. A similar cubic function was used in prehension tasks previously and was shown to yield better results than several other cost functions (Zatsiorsky et al. 2002b).
3. Entropy-like function F3. Since it is conceivable that the CNS prefers to spread efforts as evenly as possible among redundant effectors, the entropy-motivated measure:
| (5) |
was introduced by Hershkovitz et al. (1995, 1997). The equation has the similar format as the entropy function in the theory of information. It reflects the uniformity of the contact forces of fingers.
The optimal solutions were solved by applying the nonlinear multivariate function “fmincon” from Matlab’s optimization tool box (Mathworks, In., Natick, MA, USA). The quality of the optimization results was estimated by the root mean square (RMS) differences between the actual finger sharing percentages in VF and the sharing percentages predicted from optimization.
RESULTS
1. Experimental results
We describe first the results at the VF level and then at the individual finger (IF) level.
The VF level
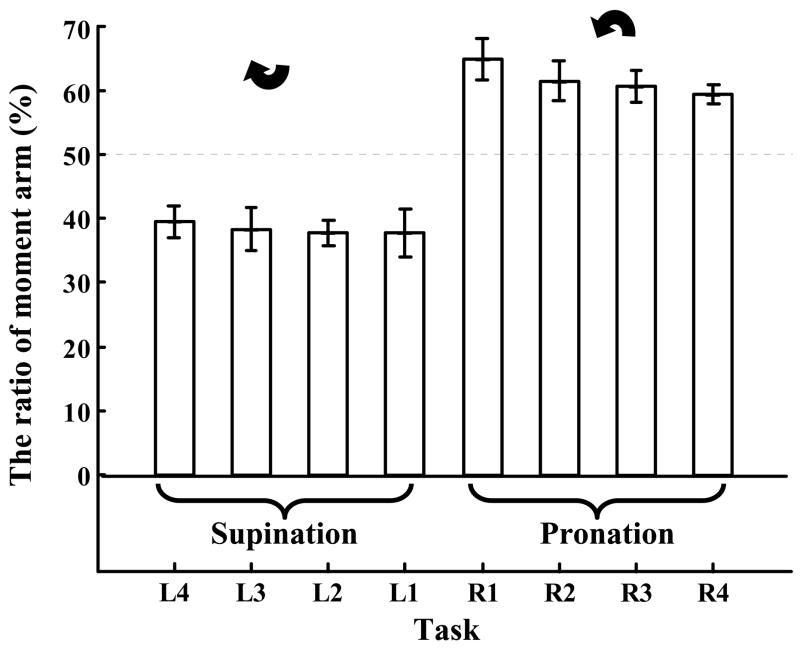
To maintain the rotational equilibrium the total moment exerted by the performer on the handle should not change after the force doubling. There are many ways of doing so. In particular, this can be achieved by maintaining the same magnitudes of the moment of normal forces Mn and the moment of the tangential forces Mt after the force doubling as before the doubling. To maintain the Mn constant after the VF force doubling the moment arm of the VF normal force should decrease to 0.5 of the moment arm before the doubling. The experimental findings are shown in Figure 3. The t-tests performed separately for the PR-tasks or SU-tasks confirmed that the obtained ratios ‘moment arm after force doubling/moment arm prior to the doubling’ were different from the ‘gold standard’ value of 0.5. In particular, in the SU-tasks the ratios in all cases were <0.4 (i.e. smaller than 0.5; p<0.05), while in the PR-tasks the ratios were >0.6 (i.e. larger than 0.5, p<0.05).
Figure 3.
The ratios ‘moment arm of the VF normal force after force doubling/moment arm prior to the doubling’ for the SU-tasks and PR-tasks. Group averages and standard errors.
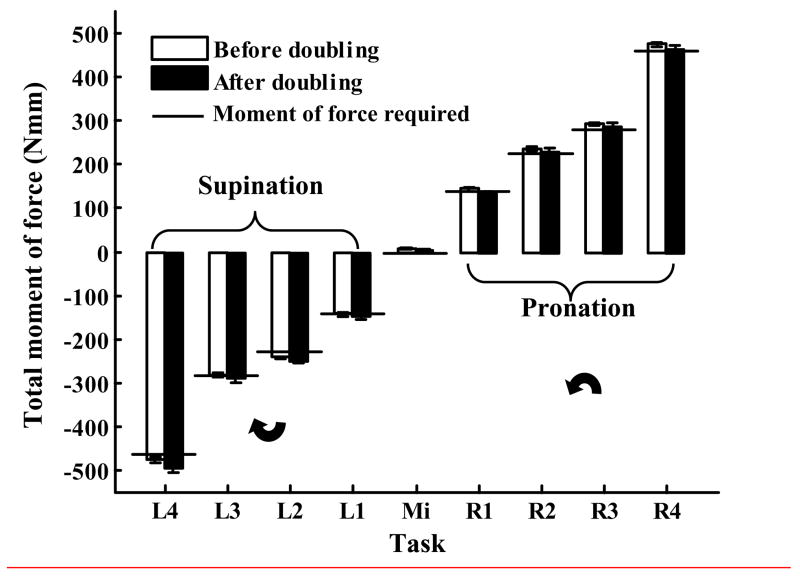
Because acording to the instruction the grasping force doubled, the deviation of the ratios from 0.5 indicated that the moments of the normal forces changed after the force doubling. The changes were however different for the SU and PR: the Mn magnitudes decreased in the supination tasks and increased in the pronation tasks, Figure 4.
Figure 4.
Changes of the moments of the normal forces after the VF force doubling. Group averages and standard errors.
Two-way repeated measure ANOVA showed that the factors FORCE, TORQUE, and the FORCE×TORQUE interaction affected significantly (p<0.001) the Mn magnitude. Note that in this analysis the factor TORQUE represents both the changes in the torque direction and the torque magnitude. The ANOVA was also performed separately for the supination and pronation effort tasks (the TORQUE factor in this case represented only the torque magnitude and had 4 levels). In the latter analysis, instead of the Mn magnitude the contribution of Mn into the total moment was considered. The effect of FORCE was significant in both the SU-and the PR-tasks (p<0.001) while the effects of TORQUE and FORCE×TORQUE interaction did not reach the level of statistical significance. Hence, the Mn changes were asymmetric, i.e. they were different for the supination and pronation tasks. The contribution of Mn into total moment was dependent on the torque direction but not on the torque magnitude.
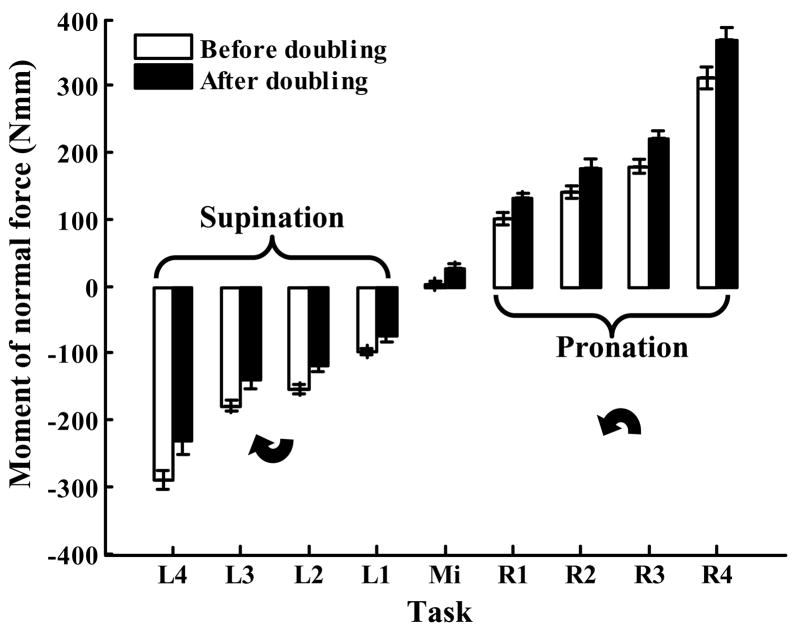
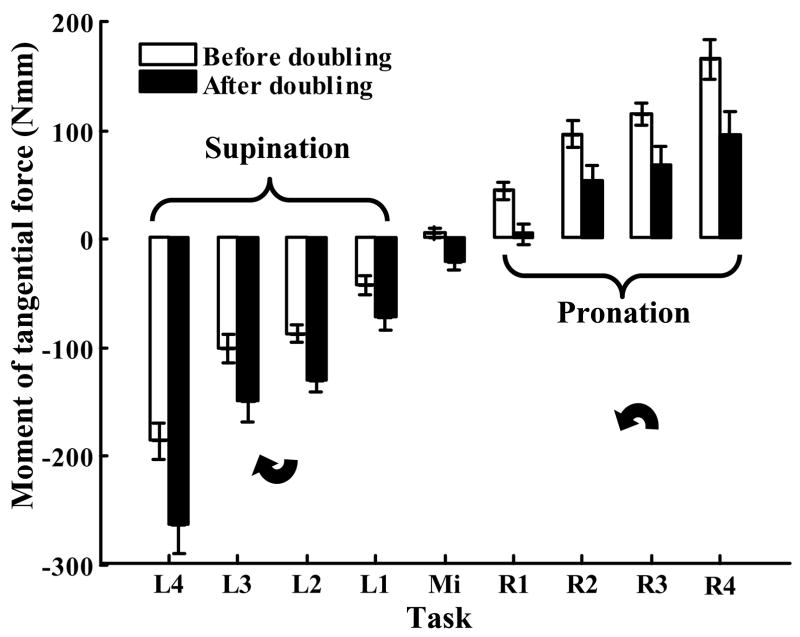
Reported effects on the moments of normal forces were complemented by the opposite changes of the moments of tangential forces Mt, Figure 5. The contribution increased in the supination tasks and it decreased in pronation tasks.
Figure 5.
The effect of the grasping force doubling on the moment of tangential forces Mt. Group averages and standard errors.
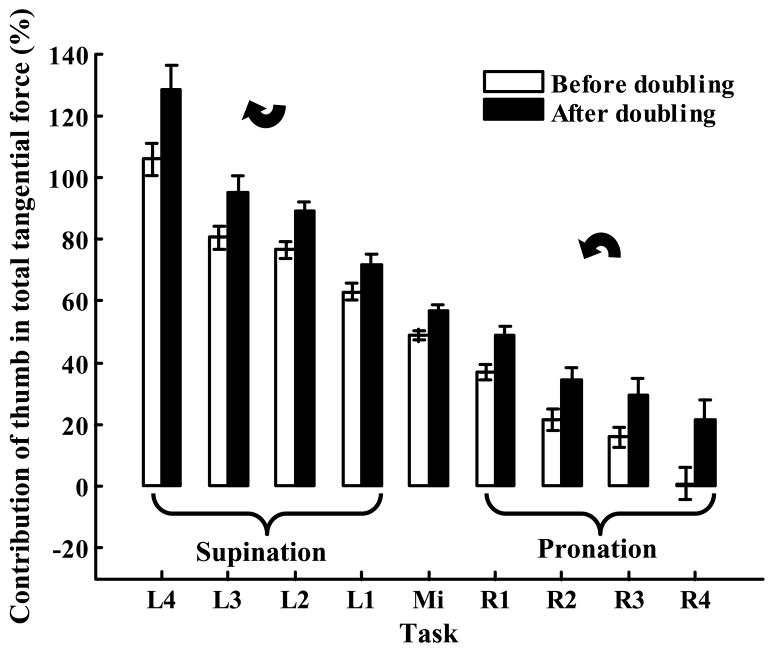
The opposite effects on the supination and pronation Mt moments were a consequence of the unidirectional changes of the thumb tangential forces: in all the tasks the contribution of the thumb tangential force to the total tangential force increased after the doubling, Figure 6. Two-way repeated measure ANOVA showed that the factors FORCE, TORQUE, and the FORCE×TORQUE interaction affected significantly the thumb tangential force (all p<0.001).
Figure 6.
Effect of the grasping force doubling on the relative contribution of the thumb tangential force into the total tangential force, %. Group averages and standard errors. Note that the total tangential force equaled the supported load and hence remained constant across the tasks. Note also that in the tasks with the large supination efforts (L4), the entire handle weight was supported by the thumb.
Because the total tangential force was constant across the tasks, the thumb tangential force increase was accompanied by the equal decrease of the VF tangential forces. As a result, the difference between the thumb and VF tangential forces changed across the tasks, and hence in accordance with equation (3) the moment of tangential forces also changed. The increase of the thumb tangential force (with simultaneous decrease of the VF force) resulted in the mentioned increase of the Mt in the supination tasks and its decrease in pronation tasks (see Figure 5).
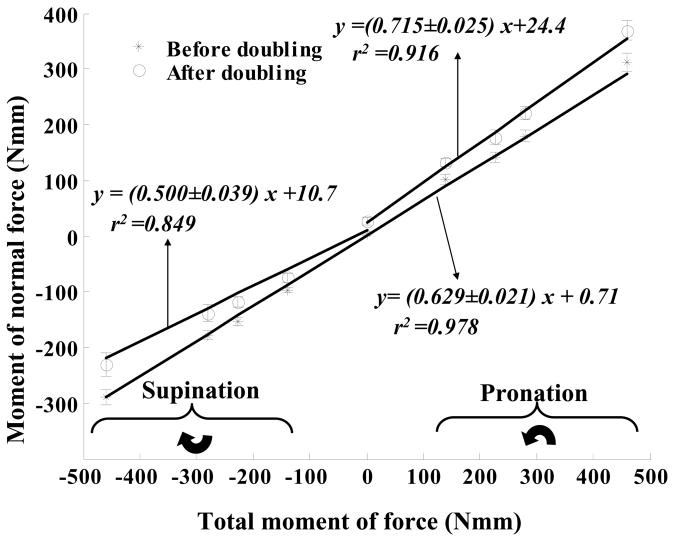
On the whole, the doubling of the grasping force induced interrelated changes of (a) the moment arms of the VF –thumb normal force couple, (b) the thumb and VF tangential forces that were different in the supination and pronation effort tasks, and (c) the contribution of the moments of the normal and tangential forces into the total moment exerted by the subjects, Figure 7. After the doubling this contribution (which can be approximately estimated from the slopes of the regression equations) was different for the supination and pronation tasks.
Figure 7.
The relation between the moment of normal forces Mn and the total moment exerted on the handle before and after the doubling. Regression equations are computed for the group data. The average and the standard deviation of the regression slope are presented in the regression equations (average ± SD).
Individual finger forces
We describe first the observed adjustments of the normal forces, and then the tangential forces.
Normal finger forces
Only in the Mi task (zero torque) the grasping force doubling was achieved by doubling the individual finger forces (approximately): the ratio ‘finger force after the doubling/finger force before the doubling’ was close to 200% for all the fingers. To test whether the individual finger force after the doubling differed statistically significantly from twice the value of the force before doubling a 1–way repeated measure ANOVA with the factor FORCE (2 levels) was performed for each finger separately. To perform the analysis the finger forces recorded before the doubling were initially multiplied by 2. The effect of FORCE was not significant (p>0.9 in all four cases). In other words, in the zero torque (Mi) task the total force increase was achieved by proportional scaling of the individual finger forces.
In the non-zero torque tasks, the ratio ‘finger force after the doubling/finger force before the doubling’ depended both on the finger and its function in the task, i.e. on whether the finger served as a moment agonist or antagonist (Figure 8). Two-way ANOVA with the factors ‘FINGER’ (4 levels) and ‘AGONIST/ANTAGONIST’ (2 levels) confirmed that the both effects were significant (FINGER: F(3, 184)=44.64, p<0.001; AGONIST/ANTAGONIST: F(1, 184)=125.68, p<0.001; interaction of the two factors: F(3, 184)=14.59, p<0.001). The same was true for the factor interaction.
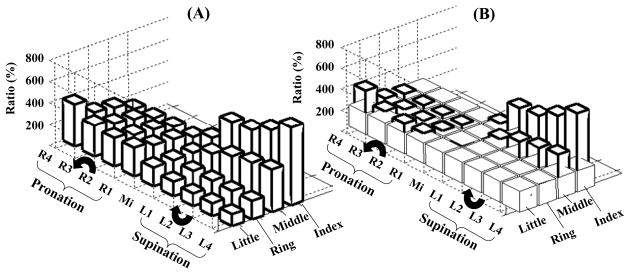
Figure 8.
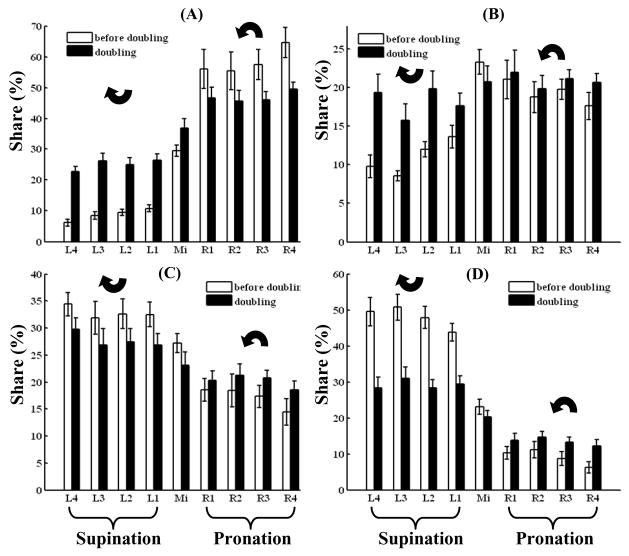
The normal finger forces after the doubling in % of their values before the doubling. A 200% value signifies the doubling of the individual finger force. Panel (A): The ratios ‘Group average force after doubling/group average force before the doubling’. Panel (B): Bold bars correspond to force values over 200%. The thin-line bars represent a 200% benchmark. The curved arrows indicate the direction of the rotation efforts, pronation or supination, as seen from the subject.
When the fingers, especially the index and little fingers, worked as moment antagonists, i.e. they assisted external torque and hence generated a moment of force that was acting against the moment required by the task, their normal forces increased much more than in the tasks where these fingers serve as torque agonists. For instance, in the supination effort tasks, where the index finger exerted a moment of force on the object in pronation, the finger increased its force production after the VF force doubling on average up to 800%. In the pronation effort tasks the corresponding force increase was less than 200%. For the little finger, in the pronation effort tasks the force increased up to 400%. The effects of the finger function (torque agonist vs. torque antagonist) on the middle and especially the ring finger forces were less striking. For the ring finger, the force after the grasping force doubling was close to 200%, although even for this finger the difference between the pronation effort tasks (the force was above 200% in all of them) and the supination tasks (the force was below 200% in all of them) is evident, see Figure 8.
Because in the non-zero torque tasks the individual finger forces did not scale proportionally with the scaling of the grasping force, the sharing percentage of the individual finger forces in the VF normal force changed with the grasping force increase (Figure 9). For the index and little fingers that are the main torque producers, the changes were uniform: when fingers served as torque antagonists their contribution to the VF force increased and when they served as torque agonists the contribution decreased. Similar tendencies—but with some exceptions— were also observed for the middle and ring fingers.
Figure 9.
The sharing % of the total normal finger force (the VF force) among the individual fingers before and after the grasping force doubling in different tasks. Group averages an standard errors. A, B, C, and D correspond to index, middle, ring and little fingers respectively.
To estimate the effects of such factors as FORCE and TORQUE MAGNITUDE on the contribution of individual fingers into the VF normal force (% of the VF force, Figure 9), a two-way Repeated Measures MANOVA was performed separately for the SU and PR tasks. The significant effects of FORCE on the sharing percentages would indicate that after the force doubling the sharing percentages change, i.e. the individual finger forces do not scale proportionally with the grasping force. The percentage contribution of the index, ring, and little fingers into the VF normal force was analyzed. To avoid redundancy, the middle finger was not included in this analysis; the sum of all four finger force contribution is evidently 100% and the middle finger sharing percentage completely depends on the sum of sharing percentages of the other three fingers. Overall significance was assessed using Wilks’ Lambda criterion. In the SU tasks, the effects of FORCE and TORQUE MAGNITUDE were both significant (p=0.03 and 0.023, respectively) while their interaction was not significant (p=0.085). In the PR tasks, the effect of FORCE was significant (p=0.045), while TORQUE MAGNITUDE and the interaction effects were not significant (p=0.165 and 0.075, respectively). Overall, in the non-zero torque tasks the individual finger forces do not scale proportionally with increase of the VF force.
Tangential digit forces
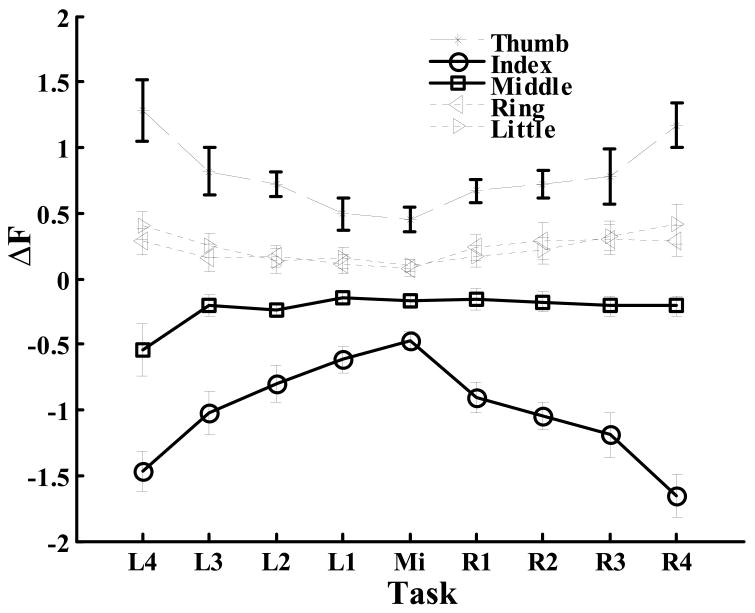
As it was described in the previous sections, the grasping force doubling was accompanied by the increase of the thumb tangential force and the concomitant decrease of the VF tangential force such that the total force acting on the object in the vertical direction stayed constant. The decrease of the VF tangential force was achieved mainly by the decrease of the tangential force exerted by the index finger (Figure 10). Paired Student’s t-tests showed that the thumb, ring and little finger’s tangential forces increased (p<0.001 in each case); index and middle finger’s tangential force decreased (p<0.001 in each case). Similarly to the analysis performed on the normal digit forces, an RM-MANOVA for overall test and RM-ANOVAs for individual fingers were employed on the changes of tangential digit forces. The factors were TORQUE DIRECTION and TORQUE MAGNITUDE. In the RM-MANOVA test, TORQUE MAGNITUDE effect was significant (p<0.001), but the effects of TORQUE DIRECTION and the interaction were not significant (p=0.125 and 0.531, respectively). The RM-ANOVA results are shown in Table 1.
Figure 10.
Effect of the grasping force doubling on the tangential forces of the individual digits. After the doubling the thumb force increases (this fact was mentioned previously, see Figure 5) while the index finger force, and consequently the VF force (not shown in the figure), decrease. The changes of tangential forces produced by other fingers are much smaller in magnitude. Group averages and standard errors.
Table 1.
The results of the two-way Repeated Measure ANOVAs on the changes of the individual finger’s tangential force in the non-zero torque tasks. The factors are TORQUE DIRECTION and TORQUE MAGNITUDE. Only p-values are presented. Statistically significant p-values are printed in bold.
| ΔFt | TORQUE DIRECTION | TORQUE MAGNITUDE | Interaction |
|---|---|---|---|
| Thumb | 0.976 | <0.001 | 0.576 |
| Index | 0.184 | <0.001 | 0.863 |
| Middle | 0.301 | 0.035 | 0.208 |
| Ring | 0.259 | 0.201 | 0.161 |
| Little | 0.622 | 0.001 | 0.711 |
Statistically significant effects of TORQUE MAGNITUDE on all digits except ring finger were observed, i.e. the changes of tangential forces after doubling were distinct for different torque magnitudes. The RM-ANOVAs confirmed that TORQUE DIRECTION (SU and PR tasks) does not influence the changes of tangential forces after doubling.
2. Optimization results
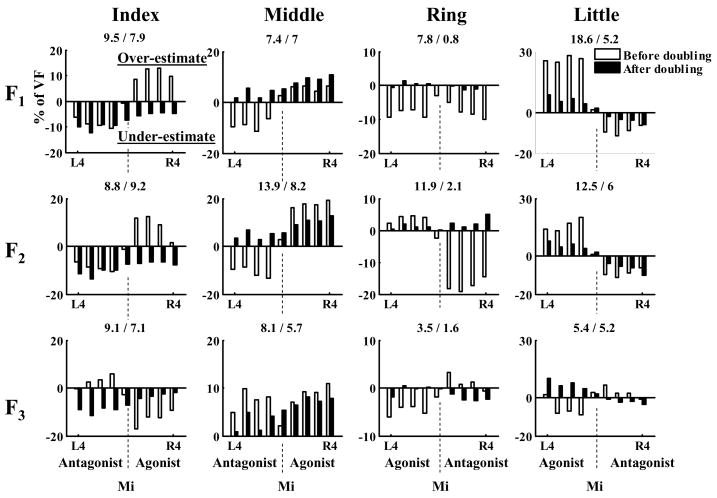
The optimization results after the force doubling were more accurate than the results before the doubling: the root mean square (RMS) differences between the actual finger sharing percentages in VF and the sharing percentages in VF predicted from optimization procedures were in all 12 cases smaller after the doubling than before the doubling (Figure 11). Before doubling, the group average RMS was 9.7 %, and after doubling the average RMS was 5.5 %. While this conclusion is rather subjective, the prediction accuracy of 5.5% may be considered not a bad fit for an optimization procedure. The average RMSs for different objective functions are 5.2%, 6.4% and 4.9%, respectively. The values are close to each other and based on the results obtained so far, we cannot claim one of the objective functions can predict the forces better than others. Three-way ANOVA was performed to inspect the effects of FORCE (2 levels: before doubling and after doubling), FINGER (4 levels) and FUNCTION (3 levels) on the RMS values. Only the main effect of FORCE was significant (p=0.002) while the other two factors had no significant effects (p>0.05 for each).
Figure 11.
The differences between the actual force sharing percentages and the values predicted from optimization (in % of the VF normal force). Before doubling (empty bars) and after doubling (black bars) results are shown. The data are for the four fingers (in columns) and three cost functions (in rows). Each panel represents the data for nine different torques, from L4 to R4. The vertical dotted lines designate the zero torque (Mi) tasks. The numbers in the panels separated by slash represent the RMS differences between the actual group average data and predicted values before and after the doubling, respectively.
DISCUSSION
We limit the discussion to the following issues: (a) maintaining the object equilibrium, (b) active versus passive tangential force generation, (c) scaling the total force, (d) effect of grasping force magnitude on the finger force pattern, (e) optimization results and their meaning for the motor control of multi-finger prehension. The items (c) – (e) answer the main questions of this study formulated in the beginning of the paper, while items (a) and (b) address some complementary issues that are however necessary to discuss the main results.
(a) Maintaining object equilibrium: mechanically necessitated and mechanically non-necessitated adjustments
In order to maintain Mn at the same level after the force doubling as before the doubling the normal force changes (‘deltas’) should generate a zero moment. This never happened, Mns after the doubling differed systematically from the moment values prior to the doubling (see Figure 4). Hence, the central controller did not solve the problem of rotational equilibrium by adjusting only the normal finger forces (which is mechanically possible); rather it preferred to prevent object tilting by simultaneous adjustments of both the normal and tangential forces. Once again, an old adage of N. Bernstein (1967, p. 69) is confirmed: “Movements react to changes in one single detail with changes in a whole series of others which are sometimes very far removed from the former both in space and in time…” Such changes can be mechanically necessary, that is to say the equilibrium could not be maintained without them, or they represented a choice made by the central controller, that is other force and moment adjustments could also maintain the object equilibrium, but the central controller preferred the observed solutions over other possible ones. The mechanically necessitated adjustments can be traced as the so-called chain effects, i.e. the cause-effect relation between the involved variables (Shim et al. 2004; Zatsiorsky et al. 2004).
The following chain effects can be traced in the observed data: (i) The VF force doubling was associated with a change of the moment arm of the VF-thumb force couple by a ratio other than 0.5, which was necessary to maintain the Mn constant; the ratio was larger than 0.5 for all pronation effort tasks and it was below 0.5 for all supination effort tasks, see Figure 3 (the reason for such coordinated changes is not known). → (ii) The above changes of the moment arm resulted in the change of moment of the normal forces Mn. → (iii) To compensate for the changes of the Mn the moment of the tangential forces M changed by an equal magnitude in the opposite direction. → (iv) The changes of Mt —its decrease in the pronation effort tasks and increase in the supination tasks— was due to an increase of the thumb tangential force and an equal decrease of the VF tangential force in all the tasks. The adjustments from stage (i) to stage (iv) were all mechanically necessitated. However, the reported decrease of the index finger tangential force after the grasping force doubling does not represent a mechanical requirement, it is a choice made by the central controller. Hence the force/moment adjustments made by the central controller to maintain the object equilibrium were only in part mechanically necessitated; other part represents the choices made by the central controller (e.g. specific changes of the VF moment arm in the pronation and supination effort tasks, the change of the VF tangential due mainly to the contribution of the index finger force, etc.). Also, the percentage distribution of the total moment among the Mn and Mt (Figure 7) is not mechanically necessitated (see Zatsiorsky et al. 2002a for the discussion). Note that the mechanically non-necessitated adjustments (those that represent a choice made by the central controller) are highly reproducible among the subjects. This consistency points toward using the same rule—or, if the decisions made by the central controller are a result of a certain optimization process, a cost function(s)—used by various performers.
(b) How are the finger tangential forces generated?
In contemporary artificial hands, both in robotics and prosthetics, the MCP joints are simple hinges that can resist tangential forces but cannot exert them (Mason, Salisbury, 1985). In people, the MCP joints have two degrees of freedom; the moments at these joints can be exerted both in the flexion-extension and ab/adduction planes. However, to which extent this option used during multi prehension is still an object of discussion and intensive research (Pataky et. al. 2004c). The passive mechanical properties of the fingers, such as stiffness of the finger tips in the tangential direction (Nakazawa et al. 2000), the tangential stiffness at the DIP and PIP joints (Pataky et al. 2005), etc., allow for providing sufficiently large resistance to the external tangential forces. The task of force sharing is mechanically redundant (one force should be distributed among the four fingers) and hence cannot be immediately determined from equations of statics. However if the resistance is provided passively, the knowledge of the finger tangential stiffness would allow for determining the force sharing among the fingers: the sharing would be in proportion to the finger stiffness (Pataky et. al. 2004c; Shim et. al., 2004). The data obtained in this paper definitely indicate that the finger tangential forces are generated actively: in particular, the substantial changes of the index finger tangential force observed after the grasping force doubling cannot be explained by the passive mechanical properties of the fingers.
After the doubling, the index finger either generated an adduction effort in downward direction (this action can be achieved by activation of the first palmar interosseous thus decreasing the magnitude of the VF tangential force exerted on the handle, either the finger provided a smaller resistance to the externally applied tangential load due to partial relaxation of the intrinsic muscles controlling the finger efforts in abduction, e.g. the abductor indicis. It is presently unknown which of the above mechanisms, the first (‘active’) or the second (‘passive’), comes about. An EMG recording is necessary to answer this question. Disregarding the mechanism of the index finger tangential force control, the bare fact that the index finger behavior plays such an important role in the VF tangential force control deserves attention.
(c) Force scaling
One of the goals of the present study was to test whether the individual finger forces scale with the total force magnitude. The scale invariance was found in several studies in which the objects of research were different: digit forces (Niu et al. 2007), (b) human elbow muscles (Buchanan et al. 1986), (c) muscles of the index finger (Valero-Cuevas 2000) and (d) static arm force generation (Pan et al. 2005). In all these cases the relative activity of the contributing elements (digits, muscles) did not change with the total force magnitude. However, for the prehension tasks it was hypothesized that this mechanism is only valid when zero moment production is required (Niu et al. 2007). The study present study confirms this hypothesis: the individual digit forces scaled with the total force magnitude, i.e. doubled, only in the Mi task when the torque on the object was zero. Hence the scale invariance is not a general law of motor control; it is valid only for some tasks. It is still possible that the scale invariance control is used when the forces are applied to fixed objects, such as in studies (b) and (c) above.
(d) Effect of grasping force magnitude on the finger force pattern
The total force doubling induced changes both in the percentage sharing of the total VF force among individual fingers (Figure 8) and in the tangential forces exerted by individual fingers (Figure 10). Hence, in the present study the pattern of finger forces in grasping, i.e. their relative values, depended on the grasping force magnitude. It is well established that people with the decreased sensitivity of the digits grasp the objects stronger than the young healthy performers. This is valid for patients with some neurological disorders (Gordon and Duff 1999; Babin-Ratté et al. 1999; Hermsdorfer et al. 1999; Serrien and Wiesendanger 1999; Fellows et al. 1998, 2001; Nowak, Hermsdorfer, 2005), seniors (Vandervoort et al. 1986; Kinoshita, Francis 1996; Cole, Rotella 2002), and healthy subjects whose finger sensitivity was intentionally decreased by cold application (Nowak, Hermsdorfer, 2003) or digital anaesthesia (Nowak et al. 2001). Unfortunately none of these studies was performed on the multifinger grasping. Hence, it remain unknown whether in the mentioned populations and conditions the performers change not only the grasping force magnitude but also the relative values of the contributing digit forces, the force sharing pattern.
(e) Optimization
When optimization methods were employed to study the finger forces before and after the VF force doubling, an important difference between these two situations was that in the first case the optimization procedure had to satisfy the requirement of both the slip and tilt prevention while in the second case only the tilt prevention requirement had to be satisfied. The differences between the optimization results in terms of their accuracy, i.e. the RMS values of the differences between the actual and predicted finger forces, were in favor of the second case, the accuracy of optimization was better after force doubling. This fact can be explained by pure technical aspects of the optimization methods, converting one of the variables (the total force exerted on the object) from the optimized variable to the task constraint may affect the optimization result. However, the finding also agrees with the previously published data that the slip prevention and tilt prevention requirements cause additive effects on the finger forces (Zatsiorsky et al. 2005) and suggests that the slip prevention and tilt prevention can be parts of different cost functions. We hypothesize that a correct way of employing the optimization methods for studying multi-finger is to use a multi-criterial optimization with one criterion related to securing slip prevention and another one to satisfying the rotational equilibrium requirements. We are presently preparing an experiment in which this hypothesis will be tested.
We acknowledge a delimitation of this study. Comparing the data before and after the doubling in the present experiment involved implicit manipulation of two task characteristics: the force magnitude and the force magnitude specification. That is, the force magnitude before the doubling was freely determined by the performer while the force magnitude after the doubling was prescribed (we thank an anonymous journal reviewer for drawing our attention to this matter). To determine the sole effect of each of these manipulations a two-stage experiment should be performed. During the first stage the grasping force should be specified at some initial level, and during the second stage, it should be specified at the doubled force value. We are going to perform such an experiment in near future.”
References
- Aoki T, Latash ML, Zatsiorsky VM. Adjustments to local friction in multifinger prehension. J Mot Behav. 2007;39:276–90. doi: 10.3200/JMBR.39.4.276-290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arbib MA, Iberall T, Lyons D. Coordinated control programs for movements of the hand. In: Goodwin AW, Darian-Smith I, editors. Hand Function and the Neocortex. Springer Verlag; Berlin: 1985. pp. 111–129. [Google Scholar]
- Babin-Ratté S, Sirigu A, Gilles N, Wing AM. Impaired anticipatory finger grip-force adjustments in a case of cerebellar degeneration. Exp Brain Res. 1999;128:81–85. doi: 10.1007/s002210050821. [DOI] [PubMed] [Google Scholar]
- Baud-Bovy G, Soechting JF. Two virtual fingers in the control of the tripod grasp. J Neurophysiol. 2001;86:604–15. doi: 10.1152/jn.2001.86.2.604. [DOI] [PubMed] [Google Scholar]
- Baud-Bovy G, Prattichizzo D, Broggi N. Does torque minimization yield a stable grasp? In: Barbagli F, Prattichizzo D, Salisbury K, editors. Multi-point interaction in Robotics and Virtual Reality. Springer Tracts for Advanced Robotic (STAR); Springer, Berlin: 2005. pp. 21–40. [Google Scholar]
- Bernstein NA. The Co-ordination and Regulation of Movement. Pergamon Press; Oxford: 1961. [Google Scholar]
- Brook N, Mizrahi J, Shoham M, Dayan J. A biomechanical model of index finger dynamics. Med Eng Phys. 1995;17:54–63. doi: 10.1016/1350-4533(95)90378-o. [DOI] [PubMed] [Google Scholar]
- Buchanan TS, Almdale DP, Lewis JL, Rymer WZ. Characteristics of synergic relations during isometric contractions of human elbow muscles. J Neurophysiol. 1986;56:1225–1241. doi: 10.1152/jn.1986.56.5.1225. [DOI] [PubMed] [Google Scholar]
- Buss M, Hashimoto H, Moore JB. Dextrous Hand Grasping Force Optimization. IEEE Trans Robot Autom. 1996;12:406–418. [Google Scholar]
- Chalfoun J, Renault M, Younes R, Ouezdou FB. Muscle forces prediction of the human hand and forearm system in highly realistic simulation. Proc IEEE/RSJ Int Conf on Intelligent Robots and Systems (IROS’04) 2004;2:1293–1298. [Google Scholar]
- Cole KJ, Rotella DL. Old age impairs the use of arbitrary visual cues for predictive control of fingertip forces during grasp. Exp Brain Res. 2002;143:35–41. doi: 10.1007/s00221-001-0965-9. [DOI] [PubMed] [Google Scholar]
- Crowninshield RD. Use of optimization technique to predict muscle forces. J Biomech Eng. 1978;100:88–92. [Google Scholar]
- Crowninshield RD, Brand RA. The prediction of forces in joint structures: distribution of intersegmental resultants. Exercise Sports Sci Rev. 1981;9:159–181. [PubMed] [Google Scholar]
- Engelbrecht SE. Minimal principles in motor control. J Math Psychol. 2001;45:497–542. doi: 10.1006/jmps.2000.1295. [DOI] [PubMed] [Google Scholar]
- Erdemir A, McLean S, Herzog W, van den Bogert AJ. Model-based estimation of muscle forces exerted during movements. Clin Biomech. 2007;22:131–154. doi: 10.1016/j.clinbiomech.2006.09.005. [DOI] [PubMed] [Google Scholar]
- Fellows SJ, Noth J, Schwarz M. Precision grip and Parkinson’s disease. Brain. 1998;121:1771–1784. doi: 10.1093/brain/121.9.1771. [DOI] [PubMed] [Google Scholar]
- Fellows SJ, Ernst J, Schwarz M, Töpper R, Noth J. Precision grip deficits in cerebellar disorders in man. Clin Neurophysiol. 2001;112:1793–1802. doi: 10.1016/s1388-2457(01)00623-x. [DOI] [PubMed] [Google Scholar]
- Fowler NK, Nicol AC. Interphalangeal joint and tendon forces: normal model and biomechanical consequences of surgical reconstruction. J Biomech. 2000;33:1055–1062. doi: 10.1016/s0021-9290(00)00080-4. [DOI] [PubMed] [Google Scholar]
- Gordon AM, Duff SV. Fingertip forces during object manipulation in children with hemiplegic cerebral palsy. I: anticipatory scaling. Dev Med Child Neurol. 1999;41:166–175. doi: 10.1017/s0012162299000353. [DOI] [PubMed] [Google Scholar]
- Hermsdorfer J, Ulrich S, Marquardt C, Goldenberg G, Mai N. Prehension with the ipsilesional hand after unilateral brain damage. Cortex. 1999;35:139–161. doi: 10.1016/s0010-9452(08)70791-3. [DOI] [PubMed] [Google Scholar]
- Hershkovitz M, Tasch U, Teboulle M. Toward a formulation of the human grasping quality sense. J Robotic Syst. 1995;19:249–256. [Google Scholar]
- Hershkovitz M, Tasch U, Teboulle M, Tzelgov J. Experimental Validation of an Optimization Formulation of the Human Grasping Quality Sense. J Robotic Syst. 1997;14:753–766. [Google Scholar]
- Iberall T. The nature of human prehension: three dexterous hands in one. Proc. IEEE Int. Conf. on Robotics and Automation; Raleigh, NC. 1987. pp. 396–401. [Google Scholar]
- Kinoshita H, Francis PR. A comparison of prehension force control in young and elderly individuals. Eur J Appl Physiol. 1996;74:450–460. doi: 10.1007/BF02337726. [DOI] [PubMed] [Google Scholar]
- Latash ML. Synergy. Oxford University Press; New York, NY: 2008. [Google Scholar]
- Latash ML, Danion F, Scholz JF, Zatsiorsky VM, Schoner G. Approaches to analysis of handwriting as a task of coordinating a redundant motor system. Hum Mov Sci. 2003;22:153–171. doi: 10.1016/s0167-9457(02)00157-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latash ML, Scholz JP, Schoner G. Toward a new theory of motor synergies. Motor Control. 2007;11:276–308. doi: 10.1123/mcj.11.3.276. [DOI] [PubMed] [Google Scholar]
- Li ZM, Latash ML, Zatsiorsky VM. Force sharing among fingers as a model of the redundancy problem. Exp Brain Res. 1998;119:276–286. doi: 10.1007/s002210050343. [DOI] [PubMed] [Google Scholar]
- Mason MT, Salisbury JK. Robot Hands and the Mechanics of Manipulation. The MIT Press; Cambridge, MS: 1985. [Google Scholar]
- Murray RM, Li Z, Sastry SS. A Mathematical Introduction to Robotic Manipulation. CRC Press; Roca Baton, FL: 1994. [Google Scholar]
- Nakazawa N, Ikeura R, Inooka H. Characteristics of human fingertips in the shearing direction. Biol Cybern. 2000;82:207–214. doi: 10.1007/s004220050020. [DOI] [PubMed] [Google Scholar]
- Niu X, Latash ML, Zatsiorsky VM. Prehension synergies in the grasps with complex friction patterns: local versus synergic effects and the template control. J Neurophysiol. 2007;98:16–28. doi: 10.1152/jn.00058.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nowak DA, Hermsdorfer J. Digit cooling influences grasp efficiency during manipulative tasks. Eur J Appl Physiol. 2003;89:127–33. doi: 10.1007/s00421-002-0759-1. [DOI] [PubMed] [Google Scholar]
- Nowak DA, Hermsdorfer J, Glasauer S, Philipp J, Meyer L, Mai N. The effects of digital anaesthesia on predictive grip force adjustments during vertical movements of a grasped object. Eur J Neurosci. 2001;14:756–62. doi: 10.1046/j.0953-816x.2001.01697.x. [DOI] [PubMed] [Google Scholar]
- Nowak DA, Hermsdorfer J. Grip force behavior during object manipulation in neurological disorders: toward an objective evaluation of manual performance deficits. Mov Disord. 2005;20:11–25. doi: 10.1002/mds.20299. [DOI] [PubMed] [Google Scholar]
- Nubar Y, Contini R. A minimal principle in biomechanics. Bull Math Biophys. 1961;23:379–390. [Google Scholar]
- Pan P, Peshkin MA, Colgate JE, Lynch KM. Static single-arm force generation with kinematic constraints. J Neurophysiol. 2005;93:2752–2765. doi: 10.1152/jn.00799.2004. [DOI] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Prehension synergies during nonvertical grasping, I: experimental observations. Biol Cybern. 2004a;91:148–158. doi: 10.1007/s00422-004-0505-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Prehension synergies during nonvertical grasping, II: Modeling and optimization. Biol Cybern. 2004b;91:231–242. doi: 10.1007/s00422-004-0506-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Tangential load sharing among fingers during prehension. Ergonomics. 2004c;47:876–89. doi: 10.1080/00140130410001670381. [DOI] [PubMed] [Google Scholar]
- Pataky TC. Soft tissue strain energy minimization: a candidate control scheme for intra-finger normal-tangential force coordination. J Biomech. 2005;38:1723–1727. doi: 10.1016/j.jbiomech.2004.07.020. [DOI] [PubMed] [Google Scholar]
- Pataky TC, Latash ML, Zatsiorsky VM. Viscoelastic response of the finger pad to incremental tangential displacements. J Biomech. 2005;38:1441–1449. doi: 10.1016/j.jbiomech.2004.07.004. [DOI] [PubMed] [Google Scholar]
- Salunkhe B, Mao WX, Tasch U. Optimal Grasping Formulations That Result in High Quality and Robust Configurations. J Robotic Syst. 1998;15:713–729. [Google Scholar]
- Santello M, Soechting JF. Matching object size by controlling finger span and hand shape. Somatosens Mot Res. 1997;14:203–212. doi: 10.1080/08990229771060. [DOI] [PubMed] [Google Scholar]
- Serrien DJ, Wiesendanger M. Grip-load force coordination in cerebellar patients. Exp Brain Res. 1999;128:76–80. doi: 10.1007/s002210050820. [DOI] [PubMed] [Google Scholar]
- Shim JK, Latash ML, Zatsiorsky VM. Finger coordination during moment production on a mechanically fixed object. Exp Brain Res. 2004;157:457–467. doi: 10.1007/s00221-004-1859-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes IA, Gardner-Morse M. Lumbar spinal muscle activation synergies predicted by multi-criteria cost function. J Biomech. 2001;34:733–740. doi: 10.1016/s0021-9290(01)00034-3. [DOI] [PubMed] [Google Scholar]
- Valero-Cuevas FJ. Predictive modulation of muscle coordination pattern magnitude scales fingertip force magnitude over the voluntary range. J Neurophysiol. 2000;83:1469–1479. doi: 10.1152/jn.2000.83.3.1469. [DOI] [PubMed] [Google Scholar]
- Vandervoort AA, Hayes KC, Belanger AY. Strength and endurance of skeletal muscle in the elderly. Physiotherapy Can. 1986;38:167–175. [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Finger force vectors in multi-finger prehension. J Biomech. 2003;36:1745–1749. doi: 10.1016/s0021-9290(03)00062-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gao F, Latash ML. Motor control goes beyond physics: differential effects of gravity and inertia on finger forces during manipulation of hand-held objects. Exp Brain Res. 2005;162:300–308. doi: 10.1007/s00221-004-2152-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gregory RW, Latash ML. Force and torque production in static multifinger prehension: biomechanics and control. I. Biomechanics. Biol Cybern. 2002a;87:50–57. doi: 10.1007/s00422-002-0321-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Gregory RW, Latash ML. Force and torque production in static multifinger prehension: biomechanics and control. II. Control Biol Cybern. 2002b;87:40–49. doi: 10.1007/s00422-002-0320-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Latash ML. Prehension synergies. Exerc Sport Sci Rev. 2004;32:75–80. doi: 10.1097/00003677-200404000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatsiorsky VM, Latash ML, Gao F, Shim JK. The principle of superposition in human prehension. Robotica. 2004;22:231–234. doi: 10.1017/S0263574703005344. [DOI] [PMC free article] [PubMed] [Google Scholar]